Towards the Use of Time-History Analysis for the Seismic Assessment of Masonry Structures

Abstract

Despite being recognized as the most accurate analysis technique for the design and assessment of masonry structures, nonlinear dynamic analysis is not commonly used in the everyday engineering practice. Reasons for this can be found in the difficulties in the selection of appropriate input ground motion records, in the limited availability of computer programs allowing the performance of time history analysis, especially for the case of masonry structures, and in the issues related with interpretation of the results in terms of performance limits. Real records are well known to be a preferable choice with respect to artificial or synthetic ground motions, but the limited availability of real records often requires scaling them, with all the concerns associated with this operation. Also, a proper selection of seismic input requires some level of expertise, which is not so common in the professional field. Regarding numerical modelling of masonry buildings, an analysis tool capable of reproducing both global seismic response and local mechanisms would be the preferable option. Existing equivalent frame models including suitable nonlinear macro-elements representative of the behaviour of structural members allow performing time-history analyses of the global response of complete 3D building models. A modified macro-element model accounting for second order effects can be suitably adopted for the analysis of local failure modes, which are mainly associated with bending-rocking behaviour and out-of-plane wall response.

1 Introduction

As reported in EC8 (clause 4.3.3.1(5) of EN 1998-1 [1]) “Nonlinear analyses should be properly substantiated with respect to the seismic input, the constitutive model used, the method of interpreting the results of the analysis and the requirements to be met.”

This basic statement well identifies the main issues related to the use of nonlinear analysis and, in particular, of nonlinear time-history analysis, which is indubitably the most accurate method for assessing the seismic response of structures, provided that these critical issues are properly tackled and suitable tools are used.

Nonlinear dynamic analysis requires the seismic input to be represented in terms of properly defined time-series (e.g. accelerograms), which need to be consistent with the seismic hazard at the site. In many building codes, this idea is associated with the concept of “spectrum-compatibility,” that will be discussed in more detail in Sect. 2.

A suitable modelling strategy for the analysis of the dynamic seismic response of complete masonry buildings is presented and discussed in Sect. 3. Specific emphasis is given (Sect. 4) on a possible approach for modelling second order effects, which are usually neglected when dealing with modelling of the in-plane behaviour of masonry walls subjected to lateral forces. This is normally an acceptable approximation for models aiming at representing the overall behaviour of masonry buildings with reasonably stiff diaphragms well connected to perimeter walls, whose behaviour is governed by the in-plane strength and stiffness of walls. Nevertheless, even in some in-plane cyclic shear-compression tests (e.g. [2]) it was shown that, in case of a clear bending-rocking response, masonry piers achieving in-plane drift ratios higher than 1 % show some evidence of the influence of second order effects.

On the other hand, as presented in [3], modelling strategies for representing the out-of-plane response of masonry walls often refer to limit equilibrium analysis, incorporating P-Δ effects, but usually approximating as rigid bodies the masonry portions involved in the considered damage mode (e.g. [4–8]). This is also the approach adopted by the Italian Building Code [9] for the seismic analysis of local failure modes in existing masonry buildings with sufficient masonry quality, for which in most cases it is possible to resort to the analysis of an equivalent system consisting of a kinematic chain of rigid bodies, connected in predefined points by rotational or sliding hinges. Such approach is then suitable for the analysis of simple local failure modes, although the rigid body hypothesis and the need to preliminarily identify the position of hinges and contact points constitute its major limitations. Moreover, the study of the dynamic response of these systems is not trivial and hence the evaluation of the expected structural performance (i.e. assessment of displacement demand) is usually carried out by means of very simplified approaches [9].

Section 4 hence illustrates the development of a macro-element model suitable for the representation of the out-of-plane wall response accounting for second-order effects. This can represent a starting point for the development of models allowing for nonlinear static and dynamic analyses of local failure modes.

Finally, an extended discussion on the definition and identification of appropriate limit states for the interpretation of the results of nonlinear time-history analysis of masonry buildings is presented in Sect. 5. Different criteria are compared and some suggestions are given based on their application to five building models.

2 Selection of Input Ground Motions for Time History Analysis

As already mentioned, the execution of time history analyses requires the definition of the seismic action in terms of appropriately selected time-series. As discussed in more detail in other works (e.g. [10, 11]), accelerograms are typically subdivided in three categories: real (or natural) records selected from accredited strong-motion databases, synthetic accelerograms generated through complex mathematical models of the seismic source and wave propagation phenomena, and artificial accelerograms generated by stochastic algorithms and constrained to be spectrum-compatible to a target response spectrum. Although the choice of the type of record to be used for defining the seismic input for time history analyses depends on the problem under study, in many cases real accelerograms are the best choice, since they are more realistic than spectrum-compatible artificial records and easier to obtain than synthetic seismograms generated from seismological source models. Since they are genuine records of ground shaking produced by real earthquakes, they retain all the ground motion characteristics (e.g. amplitude, frequency, energy content, duration, number of cycles, and phase) and reflect all the factors that influence the seismic motion (i.e., source, path, and site). Moreover they correctly reflect the correlation between the vertical and horizontal components of motion.

As the definition of seismic hazard at the site is usually performed in probabilistic terms, which also account for maximum effects potentially caused by different events, the selection of real records compatible with the expected seismic demand, usually represented in terms of response spectra, necessarily requires the selection of multiple records. Each selected record contributes in a different way to this envisaged compatibility. It is then not surprising that a significant record-to-record variability is commonly found in the selected sets and that it can be particularly relevant in case of nonlinear analysis of degrading systems like masonry structures. Hence, the outcome of the analysis implies a dispersion of the results, normally increasing as the nonlinear component of the structural response increases. This dispersion in the assessed response has to be properly coped with, when interpreting analysis results, as discussed in the following sections.

As also required by several building codes, the consistency of the selected time-series with the seismic hazard is often associated with the idea of “spectrum-compatibility”, normally consisting in imposing that the difference between the average response spectrum of the selected accelerograms and the target response spectrum is smaller than a predefined tolerance in a specified interval of structural periods (based on the fundamental period of the system to be analysed). In most cases, to satisfy spectrum-compatibility, records need to be linearly scaled to a predefined value, which can be the PGA or another selected ordinate of the target spectrum. It is important to emphasize that the selected records also need to satisfy the requirement of “seismo-compatibility” which means that they must be consistent with the regional seismotectonic and seismogenic setting, as discussed for example in [11].

The rapidly increasing number of good quality strong-motion records seems to make the use of real records a natural and easier choice for practitioners. Moreover, in recent years, several international strong-motion accelerometric databases have been developed, most of which are available over the web, which allow to interactively search events and retrieve waveforms in digital form with prescribed characteristics. Searches can be generally performed using parameters such as magnitude, epicentral distance (or some other definition of distance from the source), site classification, rupture mechanism, peak ground acceleration (PGA), peak ground velocity (PGV), and peak ground displacement (PGD). Specific tools have been developed for the selection of spectrum-compatible suites of real accelerograms, both limited to research purposes (e.g. ASCONA [11]) or available to the general public (e.g. REXEL [12]). Both ASCONA and REXEL-DISP [13] allow imposing spectrum compatibility either to the acceleration or the displacement response spectrum, the second option being preferable in case of nonlinear analysis.

Despite this, the selection of the appropriate input for time history analysis still requires some skills that are not common for practitioners. For this reason, Rota et al. [14] proposed a web application named SEISM-HOME (SElection of Input Strong-Motion for HOmogeneous MEsozones), available at the internet site http://www.eucentre.it/seism-home/, which allows an automatic and prompt definition, at any location of the Italian territory, of the seismic input represented by suites of real spectrum- and seismo-compatible accelerograms recorded at outcropping rock sites with flat topographic surface. However, these records are currently available for the 475 years return period only.

3 A Nonlinear Macro-element Model for Dynamic Analysis of URM Structures

The need for nonlinear analysis tools for complete masonry buildings arose in the late 1970s in Italy and in Slovenia, where simplified modelling techniques and analysis methods were developed and adopted in practice [15]. In the following decades, several other nonlinear models were developed and some of them are already available to practitioners and make now possible to carry out reliable nonlinear pushover analysis of masonry structures [16, 17]. These methods, generally based on the equivalent frame approach [18–20] and the macro-element discretization (single 2-node elements modelling structural members such as piers and spandrel beams), require a limited computational burden, since the number of degrees of freedom and elements in the structural model is limited.

An effective equivalent-frame formulation allowing the dynamic global analysis of whole buildings, when only in-plane response of walls is considered, is available in the TREMURI model [21, 22]. The nonlinear macro-element model representative of a whole masonry panel described in Penna et al. [23] permits, with a limited number of degrees of freedom (8), to represent the two main in-plane masonry failure modes, i.e. bending-rocking and shear-sliding (with friction) mechanisms (and their interaction), on the basis of mechanical assumptions. This model was explicitly formulated [24] to simulate the cyclic behaviour of masonry piers, considering, by means of internal variables, the shear damage evolution, which controls the strength deterioration (softening) and the stiffness degradation. The macro-element also accounts for the effect (especially in bending-rocking mechanisms) of the limited compressive strength of masonry: toe crushing effect is modelled by means of a phenomenological nonlinear constitutive law with stiffness degradation in compression. Recent developments [25] have also extended the macro-element capabilities including second order effects which can be important in case of large displacements or for other applications of the model (e.g. simulation of local/out-of-plane failure modes).

In the equivalent frame representation of the in-plane behaviour of masonry walls, each wall of the building is subdivided into piers and spandrel beams (2-node macro-elements) connected by rigid areas (nodes). The presence of ring beams, tie-rods (no-compression truss elements), previous damage, heterogeneous masonry portions, gaps and irregularities can be included in the structural model (Fig. 1).

Fig. 1

Example of macro-element modelling of a masonry wall (piers in red and spandrels in green)

The diaphragm action of floors and roofs is modelled by planar stiffening elements (orthotropic 3–4 nodes membrane elements) governing the distribution of the horizontal actions between the walls. The local flexural behaviour of the floors and the wall out-of-plane response are considered negligible with respect to the global building response, which is governed by their in-plane behaviour (a global seismic response is possible only if vertical and horizontal elements are properly connected).

In order to perform nonlinear seismic analyses of URM buildings, a set of analysis procedures has been implemented: incremental static (Newton-Raphson) with force or displacement control, 3D pushover analysis with fixed and adaptive load pattern [26], as well as 3D time-history dynamic analysis (Newmark integration method, Rayleigh viscous damping).

The results of the simulation of the response of the quasi-static tests performed on a full-scale two-story clay brick masonry building [27], reported in Fig. 2, show the capability of the equivalent-frame macro-element model in reproducing the experimental hysteretic behaviour [17].

Fig. 2

Comparison of experimental (left) and numerical (right) force-displacement curves for the two main walls of a clay brick masonry building [27]

The macro-element technique for modelling the nonlinear response of masonry panels is particularly efficient and suitable for the analysis of the seismic in-plane response of complex walls and buildings. With the inclusion of second order effects, this modelling approach could be extremely powerful also for assessing the structural response of masonry systems prone to local and out-of-plane failure modes, when subjected to static or dynamic loadings. Accounting for P-Δ effects would also slightly improve the ability of the models in assessing the wall in-plane behaviour.

Figure 3 illustrates the basic idea of the macro-element formulation. The panel can be ideally subdivided into three parts: a central body where only shear deformation can occur and two interfaces, where the external degrees of freedom are placed, which can have relative axial displacements and rotations with respect to those of the extremities of the central body. The two interfaces can be considered as infinitely rigid in shear and with a negligible thickness. Their axial deformations are due to distributed system of zero-length springs. These assumptions simplify the macro-element kinematics and compatibility relations allow obtaining a reduction of the actual degrees of freedom of the model.

Fig. 3

Kinematics of the macro-element (after [9])

A no tension model has been attributed to the zero-length springs at the interfaces, with a bilinear degrading constitutive model in compression. The axial and flexural behaviour of the two extremity joints is studied separately. The static and kinematic variables involved in joint model are the element forces N and M for the considered node and the relative displacement components w and φ (Fig. 4).

Fig. 4

Kinematic representation of node i interface in uncracked (left) and cracked (right) conditions

The constitutive model relations between the eight kinematic variables and the six nodal generalised forces (N _i , V _i , M _i , N _i , V _j , M _j ) have been derived. Internal equilibrium equations provide the generalised forces, N _e and M _e , acting on the internal degrees of freedom in the original configuration (without second order effects):

$$\left\{ {\begin{array}{*{20}c} {N_{e} = N_{j} - N_{i} } \hfill \\ {M_{e} = M_{j} - M_{i} + Vh} \hfill \\ \end{array} } \right.$$

(1)

An easy way to include second orders effect is to add the second order moment in the rotation equilibrium. The configuration is reported in Fig. 5 (right) and the relationship is given by

Fig. 5

Equilibrium in first (left) and in second order approach (right)

$$\left\{ {\begin{array}{*{20}c} {N_{e} = N_{j} - N_{i} } \hfill \\ {M_{e} = M_{j} - M_{i} + Vh^{'} + N_{e} \cdot \left( {u_{j} - u_{i} } \right)} \hfill \\ \end{array} } \right.$$

(2)

Actually the arm h′ of the moment induced by the shear force should be evaluated in the deformed shape, considering both the variation in vertical displacement (w _j  − w _i ) and the rotation of the element (h cos φ). However, in a common masonry type, the vertical displacement is small in comparison with the height of the element; similarly, the cosine of the rotation is close to unity, so that it is acceptable to substitute h′ with h.

To be consistent with the general nonlinear formulation, the second order moment can be treated as a nonlinear correction, given by:

$$M_{e}^{II} = N_{e} \cdot \left( {u_{j} - u_{i} } \right)$$

(3)

In matrix form, subdividing the elastic and inelastic terms, the macro-element constitutive equations can then be written as

$$\left\{ {\begin{array}{*{20}c} {N_{i} } \hfill \\ {V_{i} } \hfill \\ {M_{i} } \hfill \\ {N_{j} } \hfill \\ {V_{j} } \hfill \\ {M_{j} } \hfill \\ {N_{e} } \hfill \\ {M_{e} } \hfill \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {klt} \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - klt} \hfill & 0 \hfill \\ 0 \hfill & \frac{Glt}{h} \hfill & 0 \hfill & 0 \hfill & { - \frac{Glt}{h}} \hfill & 0 \hfill & 0 \hfill & { - Glt} \hfill \\ 0 \hfill & 0 \hfill & {\tfrac{1}{12}ktl^{3} } \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & { - \tfrac{1}{12}ktl^{3} } \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & {klt} \hfill & 0 \hfill & 0 \hfill & { - klt} \hfill & 0 \hfill \\ 0 \hfill & { - \frac{Glt}{h}} \hfill & 0 \hfill & 0 \hfill & \frac{Glt}{h} \hfill & 0 \hfill & 0 \hfill & {Glt} \hfill \\ 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & 0 \hfill & {\tfrac{1}{12}ktl^{3} } \hfill & 0 \hfill & { - \tfrac{1}{12}ktl^{3} } \hfill \\ { - klt} \hfill & 0 \hfill & 0 \hfill & { - klt} \hfill & 0 \hfill & 0 \hfill & {2klt} \hfill & 0 \hfill \\ 0 \hfill & { - Glt} \hfill & { - \tfrac{1}{12}ktl^{3} } \hfill & 0 \hfill & {Glt} \hfill & { - \tfrac{1}{12}ktl^{3} } \hfill & 0 \hfill & {Glt + \tfrac{1}{6}ktl^{3} } \hfill \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {w_{i} } \\ {u_{i} } \\ {\varphi_{i} } \\ {w_{j} } \\ {u_{j} } \\ {\varphi_{j} } \\ {w_{e} } \\ {\varphi_{e} } \\ \end{array} } \right\} - \left\{ {\begin{array}{*{20}c} {N_{i}^{*} } \hfill \\ {V_{i}^{*} } \hfill \\ {M_{i}^{*} } \hfill \\ {N_{j}^{*} } \hfill \\ {V_{j}^{*} } \hfill \\ {M_{j}^{*} } \hfill \\ 0 \hfill \\ {M_{e}^{II} } \hfill \\ \end{array} } \right\}$$

(4)

where the nonlinear correction terms identified by superscript “*” account for cracking, toe-crushing and shear damage effects [23], whereas the one marked as “II” accounts for the second order effects.

4 Use of the Macro-element Model Including Second-Order Effects for the Study of Rocking of Masonry Walls

This section presents some applications of the macro-element model accounting for second order effects. First of all, the model is used for the analysis of an overturning rigid block, showing its capabilities in reproducing the theoretical solutions for rocking of rigid bodies, both under static and dynamic conditions. The analyses will be then extended to the cases of deformable bodies, also accounting for the effect of limited compressive strength of masonry.

4.1 Analysis of an Overturning Block

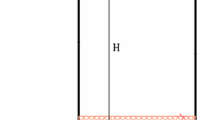
An overturning block fixed at the base (cantilever boundary conditions) represents a simple configuration to study second order effects.

Under the hypothesis of small displacements, the equilibrium at the base of the block is guaranteed by the restraint bending moment M = Fh, with F the applied horizontal force and h its height of application. In the initial linear elastic phase, second order effects can usually be neglected. After cracking, the bending moment has to satisfy equilibrium with no tensile stress acting on the cross section (partialisation). The presence of the axial force N can provide a bending capacity by means of an eccentricity e = M/N, which, even neglecting the effect of masonry crushing (assuming an infinite compressive strength), is in any case limited to half the base of the panel.

For increasing lateral displacements (i.e. block rotations), overturning occurs and second order effects become more important, contributing to a decrease of the capacity to withstand a lateral force. Figure 6 shows the limit condition for equilibrium under non-negative lateral forces, for the case in which only the self-weight is applied (left), and with a concentrated mass at the top of the block (right). In both cases, the ultimate equilibrium condition is reached when the centre of gravity of the block (or, generally, the application point of the vertical force) is aligned with the eccentric reaction force at the base (displacement u = b for infinitely strong blocks), so that a further increase in the displacement would induce overturning of the system.

Fig. 6

Limit equilibrium condition of a rigid block, subjected only to its self-weight (left) and with the addition of a concentrated mass at the top (right)

With reference to the notation reported in Fig. 6, the maximum lateral force that an infinitely rigid and strong block could withstand before activating overturning is given by

$$F_{\text{max}} = \frac{Nb}{2h}$$

(5)

Considering the deformed configuration (block rotation), the increase of the horizontal displacement of the centre of gravity causes a reduction of the lever arm of the restoring moment. Assuming a rigid block and non-negative values of the angles α and θ (see Fig. 6), the horizontal force depends on the value of b′ and h′. As previously discussed, h′ may be replaced by h:

$$F\left( \theta \right) = \frac{{Nb^{\prime}}}{2h} = \frac{{N \cdot R \cdot { \sin }(\alpha - \theta )}}{2h}$$

(6)

with $R = \sqrt {b^{2} + h^{2} }$.

For increasing values of the rotation θ, the lateral force decreases down to zero (for θ = α).

4.1.1 Effect of Elastic Deformation

For non-rigid blocks, the elastic deformation affects the lateral force-displacement curve. As reported in Fig. 7, first and second order approaches provide close results in the initial deformation phase, before cracking is reached and u and φ are coupled. Then, the second order contribution is negative, while the force due to the deformation of the interface springs increases for increasing values of u. Hence, in the first order approach, the force tends to the limit value of F _max, whereas in the second order approach, the force reaches a lower maximum value before decreasing, and it is always smaller than the one of the rigid block solution.

Fig. 7

Comparison of force-displacement curves of a macro-element with (black solid line) and without (black dashed-dotted line) second order effects. The grey continuous curve represents the rigid block solution, whereas the grey dashed horizontal line indicates the value of F _max

In order to show the effect of the Young’s modulus on the force-displacement curves, a simple numerical example was considered. It is based on a 1.0 m long, 2.0 m high and 1.0 m thick block, subjected to a vertical compression of 0.5 MPa induced by a 500 kN force applied at the top. As evident from Fig. 8, for decreasing values of the Young’s modulus E, the value of the angle θ (assuming φ ≅ θ) corresponding to cracking condition increases, shifting the maximum value of F towards higher lateral displacements. On the other hand, the increased elastic deformation reduces the maximum value of lateral force as well as the ultimate displacement, so that, decreasing E, the curves are always lower than those of stiffer blocks.

Fig. 8

Force-displacement curves of a deformable macro-element for different values of the elastic modulus in compression and comparison with the rigid block solution (dashed line)

4.1.2 Effect of Limited Compressive Strength

The consideration of a non-infinite compression strength for the material, f _m , reduces both F _max and the displacement corresponding to zero lateral strength.

If the compressive strength is limited to the value of f _m , the maximum eccentricity of the axial force N is also limited. Assuming a stress-block diagram over the compressed area of the cross section, the vertical translation equilibrium gives:

$$a = \frac{N}{{2 \cdot f_{m} \cdot t}}$$

(7)

where a is the half-length of the compressed area of the cross section.

As f _m decreases, the length of the compressed area increases, so that the maximum eccentricity of the axial force decreases, hence reducing the arm of the restoring moment. The reduced maximum value of F _max is given by

$$F^{\prime}_{ \hbox{max} } = \frac{N(b - a)}{h} = F_{ \hbox{max} } \left( {1 - \frac{N}{{2 \cdot f_{m} \cdot b \cdot t}}} \right)$$

(8)

and the displacement corresponding to zero lateral force decreases to

$$u^{\prime}_{0} = b - a = b\left( {1 - \frac{N}{{2 \cdot f_{m} \cdot b \cdot t}}} \right)$$

(9)

As shown in Fig. 9, a low value of f _m corresponds to pushover curves with lower strength for corresponding displacements and the curves are limited by the corresponding rigid body solution.

Fig. 9

Comparison of force-displacement curves for a deformable macro-element obtained for different values of f _m (black lines are for f _m  = ∞). The dashed lines indicate the corresponding rigid block solutions

4.2 Dynamic Response of a Rigid Block

The macro-element model was specifically developed to be used in dynamic simulations for the seismic assessment of in-plane masonry walls [28]. The addition of second order effects can be useful to reproduce the behaviour under strong earthquakes, where large displacements are expected. In the following, the results obtained with the macro-element for the dynamic case are compared to the classical theory of rocking of rigid bodies [29].

According to the Housner model [29], assuming that both α and θ (see Fig. 6) are small angles, the undamped dynamic motion equation describing the free vibrations of a rigid block starting from an initial rotation around the bottom right corner (named O) becomes

$$\theta^{\prime\prime} - p^{2} \vartheta = - p^{2} \alpha \quad with \quad p^{2} = \frac{NR}{{I_{0} }}$$

(10)

where I ₀ is the moment of inertia around O, N is the applied axial force and $R = \sqrt {b^{2} + h^{2} }$.

Assuming the initial conditions θ = θ ₀ and θ′ = 0 for t = 0, the analytical solution is expressed by

$$\theta = \alpha - \left( {\alpha - \theta_{0} } \right){\text{coshpt}}$$

(11)

This expression is valid for rocking motion changing alternatively the centre of rotation around the two corners at the base of the block (appropriately modifying the signs). If the impact is assumed perfectly elastic, no energy is dissipated due to the impact, the motion is periodic and its period is

$$T = \frac{4}{p}{ \cosh }^{ - 1} \left( {\frac{1}{{1 - \frac{{\theta_{0} }}{\alpha }}}} \right)$$

(12)

A very slender block, 0.2 m long, 0.1 m thick and 2.0 m high, with density equal to 1000 kg/m³ (i.e. N = 392.4 N) was modelled using the macro-element with second order effects. The mass is equal to 40 kg and the moment of inertia is equal to 13.47 kg m² around the centre of gravity and to 53.87 kg m² around the bottom corner, respectively. The block is initially rotated imposing a horizontal translation of 0.02 m to the centre of mass, corresponding to a rotation θ₀ ≈ 0.02 rad, and then left oscillating in free vibrations.

As shown in Fig. 10, the first order solution underestimates the period of vibration, whereas the second order solution provides results close to the ideal solution described by Eq. (11).

Fig. 10

Evolution of the rotation with time according to the analytical and numerical solutions. The grey dashed line is the [29] rigid block solution, whereas the black lines are the macro-element results considering (continuous) and without considering (dashed) 2nd order effects

The left part of Fig. 11 shows the rotation time-histories obtained for different values of the relative initial rotation, whereas the right part of the figure illustrates the good matching between numerically obtained period values and the trend described by Eq. (12).

Fig. 11

Left Free vibration curves of macro-elements with imposed initial rotation. Right Comparison of numerically derived vibration periods and analytical rigid block solution [29]

5 Identification of Suitable Limit States from Nonlinear Dynamic Analyses of Masonry Structures

Performance limit states are often defined by socio-economic terms, like “collapse”, “near collapse”, “collapse prevention”, “life safety”, “operational”, “fully operational”, “immediate occupancy”, “damage control” and “serviceability” (e.g. [30]). These definitions are clearly not appropriate for direct application in numerical analyses, which require a quantitative definition of performance levels, by a proper damage indicator able to represent the global seismic performance, and adequate damage thresholds expressed in terms of the selected damage indicator. Nevertheless, the quantitative translation of these qualitative and vague limit states is not straightforward. Tomaževič [31] tried to establish a correlation between these qualitative definitions and the results of experimental studies. Along the same ways, several experimental studies can be found in the literature, where cyclic in-plane tests were performed on masonry piers to describe the different deformation limits at the structural element level for the two damage modes (flexural/rocking and shear failure) of the in-plane response of masonry structures (e.g. [2, 32, 33, 34]).

A quantitative measure of structural performance can be obtained with drift/deformation quantities, as displacements and deformations are better indicators of damage than forces and therefore the identification of structural performance levels should be better based on these quantities (e.g. [35]). Significant thresholds of each limit state are needed, that should be expressed in terms of the aforementioned drift quantities and derived from some other measures of structural performance extracted from the results of nonlinear dynamic analyses. Examples of the latter could be some parameter expressing the extension of damage within the different structural elements, or the degradation of the structural response (i.e. in terms of stiffness, lateral strength, etc…) due to progressive damage. Drift thresholds are influenced by the masonry typology, the level of axial loading, the effective boundary conditions and other construction details (e.g. [36]).

Different quantitative definitions of limit states based on the results of nonlinear static analysis have been proposed in the literature, examples of which are based on the following quantitative parameters:

• 1. Significant displacements from the global pushover curve (i.e. the base shear-top displacement curve), as proposed for example in [37]. Specifically, LS2 was defined as the global displacement corresponding to the maximum base shear and LS3 as the displacement corresponding to a shear strength degradation up to 80 % of its maximum value (as also suggested in several building codes).

• 2. Global displacement thresholds corresponding to the attainment of inter-story drift limits. For example, Calvi [38] defined LS2 as the displacement corresponding to the attainment of a maximum inter-story drift of 0.3 % and LS3 as the displacement corresponding to the attainment of an inter-story drift of 0.5 %.

• 3. Some indicator of the diffusion of damage, identified for example in [36] by monitoring the level of damage reached in each wall panel.

For the assessment of masonry structures the limit states of interest can be described as:

• LS1-immediate occupancy,

• LS2-damage limitation,

• LS3-life safety,

• LS4-near collapse.

An analytical study with the objective of proposing a suitable definition of significant limit states for masonry buildings, applicable to the results of incremental dynamic analyses (IDA, [39]) was conducted recently by the authors [40]. The study concentrated on two intermediate limit states (LS2 and LS3), as their identification appears more uncertain and somehow more critical than that of the first and last limits. The identification of LS4 was not addressed, because the definition of the near collapse limit state from the results of numerical analyses is really a difficult task. With reference to nonlinear dynamic analyses, this limit state could be identified by monitoring the IDA curve for each earthquake record and identifying the point for which the slope of the curve approaches zero, as suggested by Ibarra and Krawinkler [41]. However this definition is really vague and it does not easily allow a univocal identification of this limit state. Moreover, as also discussed by Zareian and Krawinkler [42], evaluation of near collapse structural response parameters is strongly related to issues such as assumptions in the structural model, computer program used for the analysis, numerical convergence and stability of the solution. Therefore, the evaluation of LS4 was left aside.

The identification of limit state indicators was approached by applying some proposed criteria to five building models of existing stone masonry buildings. The methodology included the identification of performance limit states from both the results of nonlinear static and dynamic analysis and the comparison of the results obtained in the two cases.

5.1 Drift Quantities Selected to Describe and Compare Performance Levels

To be able to compare alternative definitions of limit states, the significant thresholds derived from different damage quantities need to be expressed by the same drift/displacement quantities. Mouyiannou et al. [40] interpreted all the analysis results according to two drift quantities, i.e. the maximum inter-storey drift δ _max and a weighted average drift δ _w , derived from nodal displacements and from element drifts, respectively. The maximum inter-storey drift δ_max is the maximum value of pier drift δ _i , obtained as the absolute difference of nodal displacements divided by the inter-story height.

The weighted average drift δ _w is calculated as the average of the drifts of all the elements of the critical story, weighted on their area, according to the formula:

$$\bar{\updelta }_{\text{w}} = \frac{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{\text{n}} ({\text{A}}_{\text{i}} \updelta_{\text{i}} )}}{{\mathop \sum \nolimits_{{{\text{i}} = 1}}^{\text{n}} {\text{A}}_{\text{i}} }}$$

(13)

where A _i is the area of pier i, δ _i is the drift of pier i and n is the total number of piers of the critical storey, identified as the storey where damage concentrates. The values of δ _i are the element shear drifts, which only account for the shear element deformation, i.e. they are computed by removing the flexural deformation and rigid rotation components from the element drift. This shear drift is an output of the macro-element model, to which the shear behaviour with stiffness degradation and strength deterioration is directly related, and hence it is considered a suitable indicator of the level of damage in the element. The criteria proposed in [40] for the identification of each limit state are described in the following sections.

5.2 Identification of LS1 (One Criterion), LS2 and LS3 (3 Criteria)

The first limit state can be identified as the displacement that corresponds to the first pier reaching its maximum shear resistance.

Three different criteria were instead investigated to identify LS2 and LS3, which are not directly based on drift quantities, but also described by a parameter that is representative of the evolution of the structural condition during the nonlinear dynamic analysis. Each criterion is based on consideration of different damage indicators, all of them trying to synthesize the overall structural behaviour, i.e. the extension of damage to the structural elements (criterion 2) or the degradation of the structural response with progressive damage (criterion 1).

The drift quantities corresponding to the attainment of the limit states according to the different criteria were evaluated and compared among each other, to verify whether these definitions of the limit states provide stable and reasonable results in terms of the deformation conditions reached by the structure during the dynamic response. The drifts were also compared to the results of similar criteria applied to pushover analysis.

The criteria proposed to define the damage limitation limit state (LS2) and life safety limit state (LS3) from the results of incremental dynamic analyses (IDA) are discussed in the following. For LS2, an extra limitation to the maximum inter-story drift, which should not exceed the value of 0.2 %, was also adopted.

5.2.1 Identification of LS2 and LS3 from Total Base Shear (Criterion 1)

Similarly to the definition of limit states from the pushover curve reported in [37], for the case of time-history analysis and for each earthquake record analysed, LS2 is attained at the analysis step for which the shear resistance reaches its maximum value and LS3 at the step where it drops to 80 % of its maximum value. The drifts corresponding to the two limit states are then derived and their average values (among the earthquake records used for the analyses) are calculated. This criterion is fast and easy to apply and it does not require any engineering judgment or subjectivity, as the definition of the limit states is quantitative and objective.

5.2.2 Identification of LS2 and LS3 Based on the Percentage of Pier Area Failing (Criterion 2)

According to criterion 2, LS2 and LS3 are identified based on the number and percentage of piers achieving the maximum shear drift (predefined value). A reasonable value for maximum shear drift could be 0.4 %, as suggested in the EC8-3 [43], although it makes reference to a different definition of element drift. The drift mentioned in the codes is the total element drift, including both shear and flexural components and eventually excluding rigid motions, whilst in the described analytical work the flexural component is removed. The use of the limit of 0.4 % indicated in the codes was considered appropriate, because it is derived from experimental evidence of in-plane cyclic tests on mainly squat masonry panels, in which it can be assumed that, when shear failure occurs, the shear deformation component is the one representative of the degradation of the structural response and it is prevailing over the flexural one.

LS2 (damage limitation) is assumed to occur when the first pier reaches the predefined value of shear drift. In order to provide results meaningful for comparison to the results from other criteria, the results are expressed in terms of the average drift values (as defined in Sect. 4.1) calculated from all the earthquake motions used for the analysis.

LS3 corresponds to an appropriately defined level of damage extension, which is expressed in terms of the percentage of the area of the piers that have attained the maximum shear drift with respect to the total pier area, i.e.:

$$A_{fp} [\% ] = \frac{{\mathop \sum \nolimits_{i}^{m} A_{pi} }}{{\mathop \sum \nolimits_{j}^{n} A_{pj} }} \cdot 100$$

(14)

where m is the number of the piers which attained the maximum shear drift and n is the total number of piers. For each PGA level considered for the analyses, and for each earthquake record, the percentage of the pier area failing is calculated and compared with a predefined target percentage. For each considered building, LS3 is then attained when the average (among all the earthquake records used) percentage area reaches the predefined drift limit.

Attention should be taken when evaluating the appropriate target percentage area for LS3, since the procedure is strongly dependent on its definition, which needs to be identified case by case and whose value cannot be considered as general. The value needs to be selected based on engineering judgment and should be associated with drift values which are in accordance with those derived from nonlinear static analyses. In addition, this percentage should guarantee collapse prevention, i.e. limited lateral strength degradation, since the criterion is applied to identify the life safety condition. A reasonable percentage, representative of the results, was considered to be 50 % of the total pier area in the direction of analysis.

5.2.3 Identification of LS2 and LS3 from PGA-Drift Curves (Criterion 3)

The third criterion is applied to the so-called IDA curves, reporting the level of PGA versus an appropriately defined drift quantity. Each curve is a multi-linear curve obtained by joining the drift values calculated for subsequent levels of PGA examined. The average PGA-drift curve for the critical story of each building can be evaluated by plotting the average drifts among the earthquake records for each PGA.

LS2 can be identified at the first significant change of slope in the average curve. This is related to an increased rate of drift variation as a function of PGA, which can be seen as representative of an increase of structural damage.

LS3 can be identified as the range of drifts between which the slope of the curve degrades reaching a predefined percentage of the initial slope. This percentage is selected according to engineering judgment to represent a damage level adequate for the life safety limit state and should provide drift values in agreement with the results of nonlinear static analysis. Based on the results obtained in the considered analytical study, and specifically on the comparison of the corresponding drift values with those derived from the results of nonlinear dynamic analyses by applying the other criteria and the results of nonlinear static analyses, a percentage equal to 7 % of the initial slope was selected (after having tried different values up to 10 %).

5.3 Application of Limit State Identification Criteria to the Results of Nonlinear Dynamic Analysis of Existing Masonry Buildings

The identification criteria discussed above were applied to 5 building prototypes, selected as representative of different structural typologies of unreinforced stone masonry buildings. Their models are shown in Fig. 12. All the analyses were performed along the x-direction indicated in the figure.

Fig. 12

Analysed structural configurations (after [40])

All buildings were assumed to have stiff diaphragms. Out-of-plane failure mechanisms are assumed to be prevented by proper connections and detailing.

The mechanical properties of stone masonry adopted in the model were defined according to an extended experimental campaign carried out in Pavia in the last years [44, 45], consisting of tests on mortar, vertical compression and diagonal compression tests on wallettes, cyclic shear compression tests on walls, followed by full-scale shaking table tests on three prototype buildings [46, 47]. The average experimental values of the elastic modulus, E, the shear modulus, G, the masonry density, ρ, and the compressive strength of masonry, f _m were used. The values used for the initial shear resistance for zero compression, f _v0 and the friction coefficient, μ were instead obtained from the calibration of the macro-element model on the results of cyclic in-plane tests of masonry piers [33].

Incremental dynamic analyses were performed using seven real spectrum-compatible earthquake records, selected using the program ASCONA [11] and scaled to increasing values of PGA (from 0.05 to 0.60 g) to represent different levels of seismic severity. The real records were selected to be compatible in the mean with the EC8-1 [1] type 1 acceleration response spectrum, anchored to a PGA of 0.2 g, selected to be approximately a central value of the seismic intensities considered for the analyses. This choice was based on the attempt of limiting the scale factors applied to the records.

5.3.1 Resulting Drift Thresholds for LS1, LS2 and LS3

LS1 was identified as the state corresponding to the first pier reaching its maximum shear strength. The average values (between the 7 earthquake records analysed) of maximum element drifts corresponding to LS1 are presented in Fig. 13.

Fig. 13

Maximum element drifts corresponding to the attainment of LS1 (average of 7 records)

The average value derived from all buildings is 0.12 %, in agreement with the experimental results obtained in [33], according to which the maximum shear resistance of a stone masonry element is reached for a maximum element drift in the range of 0.10–0.15 %. The results confirm that the drifts corresponding to LS1 are not depending on the building typology, nor on the earthquake records, as they are only a property of the numerical model and of the masonry typology.

The drift values corresponding to the attainment of LS2 and LS3 were identified by applying the three criteria described previously. The derived drift quantities, namely the average (between the earthquake records used) maximum inter-story drift (δ _max) and weighted average story drift (δ _w ), resulted by the application of the criteria for the identification of LS2 and LS3 are presented in Figs. 14 and 15, respectively, for all the buildings analysed. Black diamonds correspond to δ _max and grey circles to δ _w . The error bars represent the coefficient of variation (C.o.V) resulting from record-to-record variability.

Fig. 14

Average drift quantities resulting from the application of criteria for LS2

Fig. 15

Average drift quantities resulting from the application of criteria for LS3

As observed in Fig. 14a, the application of criterion 1 for LS2 identification results in values of both the drift quantities between 0.1 and 0.2 %, with the only exception of building E. In this case, both drifts are equal to 0.29 %, which in case of δ _max exceeds the limit value of 0.2 %. However the limits for building E are characterized by the largest coefficient of variation. Apart from the case of building B, the C.o.V. of the values of δ _w is always lower than that of δ _max, although their values vary significantly from building to building.

The range of drift values obtained by criterion 2 is larger than the ones resulting from criterion 1, with values between 0.1 and 0.38 % (Fig. 14b). Nevertheless the values of C.o.V. are lower than the values resulting from the other criteria, indicating a smaller dependence of criterion 2 on the record-to-record variability.

Regarding the average drift values obtained by criterion 3 for LS2 (Fig. 14c), similar values around 0.1 % are observed for all buildings except for building A, which attained a significantly higher value. It has to be underlined that the C.o.V. has very large values for criterion 3, showing a high dependency of the results of the criterion on the record-to-record variability.

The drift values corresponding to LS3 derived by criterion 1 are ranging between 0.25 and 0.65 %. The maximum C.o.V., equal to 17.5 %, is found for the case of δ _w for building B, and is small compared to the values of C.o.V. resulting from the application of the other criteria for the derivation of LS3. It can be noted that, as observed from the application of criterion 1, the average values of the two drift quantities for LS3 are quite similar to each other, with the exception of building D.

The drift values of LS3 obtained by criterion 2 (Fig. 15b) correspond to the level of PGA for which the average percentage (among the results from seven earthquakes) of piers reaching the maximum shear drift exceeds 50 % of the total pier area. A rather wide range of drift is obtained, with buildings A and D having similar values at the lower bound of the range and buildings B, C and E having similar values at the higher bound of the range. It is important to notice the very large C.o.V. resulting for all buildings, indicating the significant dependence of the results of this criterion on the record-to-record variability.

As previously explained, the results of criterion 3 are expressed by two values of drift corresponding to the upper and lower value of the drift range for which the slope of the IDA curve drops below a predetermined percentage of the initial slope. The results (Fig. 15c) show a significant variability from building to building, both in terms of the range width and of the values corresponding to the upper and lower bound drift values. This is related to the level of discretization of the PGA values used for the analyses and to the slope of the curve in the drift range of interest. Also, the very large values of C.o.V. indicate the strong dependency of the results on the record-to-record variability.

5.4 Comparison of the Applied Criteria and Selection of the Optimal Criteria for LS2 and LS3 Identification

This section compares the results derived by the application of different criteria to the results of nonlinear dynamic analysis and also to the results of nonlinear static analysis. Figures 16 and 17 correspond to the case of LS2 and represent the values of weighted average story drift and its C.o.V. due to record-to-record variability. The choice of reporting only the results for LS2 in terms of weighted average story drift is based on the fact that it provided a better match with the results of pushover analyses than the maximum inter-story drift.

Fig. 16

Weighted average drift limits for LS2 derived from the results of nonlinear dynamic analysis by applying the three identification criteria and from the results of nonlinear static analysis

Fig. 17

Coefficient of variation of the values of weighted average story drift limits of LS2, due to record-to-record variability

It can be noted that criterion 1 and criterion 3 are reproducing quite well the results obtained from pushover analysis, with the exception of building E and A, respectively for the two criteria. Criterion 2 provides higher values of drift than all other criteria for buildings C and D and, in general, a good agreement with the results obtained from pushover analysis cannot be found. Figure 17 shows that criterion 3 has a significantly higher value of C.o.V. with respect to the others. For both criteria 1 and 2, building E has significantly higher values of C.o.V., which may be related to the marked structural irregularity of the building. Consequently, both criteria 1 and 2 appear to be suitable for the identification of LS2, always combined with the limitation of the maximum inter-story drift to the value of 0.2 %.

A comparison of the drift limits provided by the different criteria for LS3 is shown in Figs. 18 and 19, in terms of the average value of maximum inter-story drift and its C.o.V. due to record-to-record variability, respectively. For this limit state, results are presented in terms of maximum inter-story drift, since this drift shows a better agreement with the results of nonlinear static analysis.

Fig. 18

Maximum inter-story drift values for LS3 derived from the results of nonlinear dynamic analysis with the three identification criteria and from the results of nonlinear static analysis

Fig. 19

Coefficient of variation of the values of maximum inter-story drift for LS3, due to record-to-record variability

The histogram of Fig. 18 shows that the different criteria provide different results in terms of attained drifts, as expected since each criterion is based on consideration of different quantities. In order to apply criteria 2 and 3, some reasonable target values have been assumed for the percentage of pier area failing and the percentage of the initial slope, respectively. It is generally noticed that there is no unique value of percentage to be set for criteria 2 and 3 to guarantee that the requirements of the other criteria will be met for all buildings. For criterion 3 and LS3, the considered target value of the slope reduction with respect to the initial slope (7 %) leads to drift ranges which are not always in agreement with the results of criterion 1 and 2. In case of maximum inter-story drift, even for building E, the value produced by criterion 1 is outside the range of criterion 3. Criterion 2 provides instead results within the range defined by criterion 3 only for buildings A, B and C. The results obtained from pushover analyses are in general more consistent with the results from criterion 1 rather than with those obtained from the other two criteria, with the only exception of building E. This could be expected, as criterion 1 is analogous to the definition of limit states used for pushover analyses. Regarding building E, it should be noted that the structure is irregular in plan and in elevation and therefore the application of nonlinear static analysis is questionable and the validity of its results is not guaranteed.

It is obvious from Fig. 19 that the drifts derived from criterion 1 for LS3 have a much smaller variability than that corresponding to the other criteria.

The aforementioned difficulties in the application of criteria 2 and 3, in addition to the significantly larger coefficient of variation of the drifts obtained by these criteria, led to the selection of criterion 1 as the optimum for the identification of LS2 and LS3 from the results of nonlinear dynamic analysis. Criterion 1 is indeed the criterion providing the most stable and consistent results and it is the least dependent on the record-to-record variability. Moreover, it is equivalent to the definition of LS2 and LS3 based on the results of nonlinear static analyses and it is the most straightforward to apply, as it does not require any particular engineering judgment nor the definition of target values.

6 Conclusions

As stated in the introduction, the use of nonlinear time-history analysis for masonry structures requires suitable modelling approaches and an appropriate selection of input ground-motion records. The latter is an issue common to all structural types and several solutions available in the literature are briefly discussed in Sect. 2.

The TREMURI computer program, concisely presented in Sect. 3, includes modelling and analysis features specifically developed for the dynamic analysis of entire masonry buildings. The modified two-dimensional macro-element model which accounts for second order effects represents a promising tool for the nonlinear static and dynamic analysis of rocking motion of masonry walls, with particular emphasis on the study of out-of-plane response and local failure modes. The comparison of static and dynamic analysis results against experimental results and theoretical solutions confirmed that the upgraded model is able to capture the main aspects of the response of single blocks or masonry walls with rocking behaviour. Future developments of the model will necessarily be oriented to include energy dissipation effects occurring in dynamic response.

What is still missing is a well-defined method for identifying the structural performance levels based on damage and/or displacement/deformation indicators, which would help in the interpretation of the results of dynamic analyses and may support a broader application of the performance-based procedure with incremental time-history analysis of masonry buildings. A procedure for the identification of limit states has been presented in this paper. The first limit state considered, i.e. immediate occupancy (LS1), was identified as corresponding to the first pier reaching its maximum shear strength. The definition of LS2 (damage limitation) and LS3 (life safety) from the results of time-history analyses was more problematic and therefore three different criteria were proposed and tested, each one concerning requirements on different quantities. The first criterion was based on global lateral strength evolution, the second criterion on damage diffusion and the third criterion on the degradation of the structural response for increasing levels of ground motion. In order to compare the results of the different criteria (which are based on completely different quantities) and to make sure that they provide reasonable results in terms of deformation capacity, conveniently defined drift quantities were associated with the limit states identified with the different criteria. For each limit state, the best criterion was selected together with the associated drift quantity providing the most stable (and the least dependent on the record-to-record variability) and consistent results.

The reported study was limited to a small number of building configurations and a specific masonry typology. Other important parameters should also be explored in order to verify the adequacy of the proposed criteria for the identification of relevant limit states. In addition to the previous, the consistency of the proposed approach with experimental results and empirical observations should be verified.