Investigating the Role of Network Topology and Dynamical Regimes on the Dynamics of a Cell Differentiation Model

Abstract

The characterization of the generic properties underlying the complex interplay ruling cell differentiation is one of the goals of modern biology. To this end, we rely on a powerful and general dynamical model of cell differentiation, which defines differentiation hierarchies on the basis of the stability of gene activation patterns against biological noise.

In particular, in this work we investigate the role of the topology (i.e. scale-free or random) and of the dynamical regime (i.e. ordered, critical or disordered) of gene regulatory networks on the model dynamics. Two real lineage commitment trees, i.e. intestinal crypts and hematopoietic cells, are compared with the hierarchies emerging from the dynamics of ensembles of randomly simulated networks.

Briefly, critical networks with random topology seem to display a wider range of possible behaviours as compared to the others, hence suggesting an intrinsic dynamical heterogeneity that may be fundamental in defining different differentiation trees. Conversely, scale-free networks show a generally more ordered dynamics, which limit the overall variability, yet containing the effect of possible genomic perturbations. Interestingly, a considerable number of networks across all types show emergent trees that are biologically plausible, suggesting that a relatively wide portion of the networks space may be suitable, without the need for a fine tuning of the parameters.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

In the last years a dynamical interpretation of gene regulation has gained an always greater attention, as a complement to the static consideration of the interactions among genomic entities, as classically done through the systems-biology approach [17]. The focus switches from the static description of the involved entities and interactions to the analysis of the emergent collective behaviors, that are the gene activation patterns characterizing the different phenotypic functions of cells, such as cell types or modes. Each organism is, in fact, characterized by a unique gene regulatory network, but is able to exhibit a broad range of distinct phenotypes. Any (phenotypic) function is determined by a specific gene activation pattern, which is the result of the joint dynamical interaction among genes.

Accordingly, gene regulatory networks (GRNs) can be modeled as dynamical systems and the focus is on the analysis of their “attractors” [14, 21, 30]¹. Many different mathematical and computational models aimed at representing the dynamics of GRNs have been developed through the years, with different goals and applications and most of them are rooted in complex systems science and statistical physics (see, e.g., [38] for a recent review).

In particular, we here present a study regarding a dynamical model of cell differentiation², introduced in [39] and based on Noisy Random Boolean Networks (NRBNs, [27, 31]). This simplified model of gene regulation considers genes as simply active/inactive and describes simplified regulatory interactions (not explicitly considering the underlying biochemical machinery), focusing on the dynamical behaviour emerging from the interaction of the genes. In line with the complex systems approach the major goal is to investigate the generic properties of gene networks, that are those properties shared by a broad range of systems and organisms. To this end, a powerful methodological means is that provided by the statistical analysis of ensembles of randomly simulated networks with specific features, in order to scan the huge space in which real networks, on which complete information is still missing, might be found. Despite the underlying abstractions, this modeling approach was proven fruitful in describing properties of real networks, as in, e.g.,[21, 22, 29, 33, 34, 36].

The model of cell differentiation we here analyze is abstract and general, i.e. it is not referred to any specific system or organism and it is based on two specific dynamical properties of the attractors of GRNs: their robustness against random or selective perturbations (i.e. genomic mutations/alterations) and their reachability, defined as the likelihood of observing a certain attractor. Starting from the underlying hypotheses that biological noise and specific perturbations can trigger transitions among the GRN attractors (i.e. the gene activation patterns) and that higher level of noise were detected in less differentiated cells [8, 10, 11, 13, 24], two constraints must be respected: $(i)$ the attractors of a specific cell type must be sufficiently robust against perturbations not to compromise the functioning of the cell, $(ii)$ in less differentiated cell types attractors must be sufficiently sensitive to perturbations to account for different cell fates when differentiating. These constraints are satisfied in our model by assuming that: $(i)$ cell types or modes are characterized by sets of attractors in which the GRN can wander via noise or specific signals; $(ii)$ the process of progressive specialization is characterized by a gradual improvement of the noise-control mechanisms that hinder the transitions, from less differentiated cells, sensitive to noise, to fully differentiated stages, robust against noise. In this way it is possible to define a hierarchy connecting the differentiation levels and cell fate decisions are then driven by stochastic fluctuations or triggered by specific signals.

Many important features of the differentiation process are reproduced by the model, such as: $(i)$ the presence of different degrees of differentiation, that span from totipotent stem cells to fully differentiated cells in a well-defined hierarchy, which determines a lineage tree; $(ii)$ the stochastic differentiation, according to which populations of identical multipotent cells stochastically generate different cell types; $(iii)$ the deterministic differentiation, in which specific signals trigger the progress of multipotent cells into more differentiated types, in well-specified lineages; $(iv)$ the limited reversibility in which, under the action of appropriate signals, the cell can revert its lineage specification; $(v)$ the induced pluripotency, according to which fully differentiated cells can come back to a pluripotent state by modifying the expression of specific genes [41]; $(vi)$ the induced change of cell type, in which the modification of the expression of few genes can directly convert one differentiated cell type into another.

The emerging lineage commitment tree can be matched against real differentiation trees as those in Fig. 1, through simple tree-matching algorithms. The analysis of a large number of GRNs matching/non-matching real trees can then provide some cues for explaining the properties ruling the complex differentiation interplay.

Thus, the focus of this work is to analyze the influence of: $(i)$ the topology and of $(ii)$ the dynamical regime of the GRNs on the key dynamical properties and especially on their robustness and reachability, with particular regard to the emerging differentiation hierarchy. In particular, two real differentiation trees will be targeted by our model, intestinal crypts and hematopoietic cells.

In regard to the former analysis, classical studies on RBNs and NRBNs involve random topologies (i.e. Erdos-Renyi-based [9]), which determine a Poissonian distribution of the connection. Even though present data still do not allow to draw definitive conclusion on the topology underlying real GRNs, it is sound to investigate the relation that different kinds of topologies may have on the overall emerging behaviour. In particular, scale-free networks [3] have raised a considerable interest and were shown to approximate several networks, including metabolic and protein networks³. Therefore, we here present the analysis of a study comparing the behaviour of NRBNs with random and scale-free topologies.

The second analysis concerns the influence that the dynamical regimes have on the properties of the GRNs relevant to the differentiation model. In short, the dynamical regime of a RBN is defined on the basis of the sensitivity to the initial conditions, that is the response to small perturbations. If small perturbations tend to lead to different attractors, i.e. the perturbation propagates, the network can be considered as disorderered (sometimes refered to as chaotic) and vice versa. Networks characterized by disordered regimes are (on the average) characterized by a larger number of longer attractors and vice versa. It was analytically proved that by varying certain key structural parameters of RBNs it is possible to switch across the dynamical regimes. A very interesting dynamical region is at the boundary between disordered and ordered phase and is defined as “critical”, sometimes referred to as the “edge of chaos” [23]. It was hypothesized the biological systems, and GRNs in particular, may live and evolve in this specific region, which would allow an optimal trade-off between robustness and evolvibility [21]. Experimental evidences in support of this hypothesis are provided, e.g., in [29, 33, 36]. In this work we aim at investigating how the dynamical regime can influence the properties of the cell differentiation model, with specific regard to the suitability for a matching with real differentiation trees.

As specified above, the two specific biological systems that were chosen as test beds for the model are intestinal crypts and hematopoietic cells. Intestinal crypts are invaginations in the intestine connective tissue in which tumors are supposed to originate from some partially known gene and pathway alterations affecting the stem cell niche [1]. A complex differentiation process rules the overall homeostasis, in terms of stratification of cell populations of distinct types, coordinate migration, dynamic turnover, etc. Conversely, in hematopoietic cells, the differentiation can be interpreted as a trajectory among attractors, involving the transcriptome as the state space of cell populations and the miRNome as tuning mechanism, and that starts from multipotent hematopoietic stem cells giving rise to a hierarchy of progenitor populations with more limited lineage potential, eventually leading to mature blood cell types [Felli et al. 2010].

In both cases we are interested in comparing the already mapped lineage trees (Fig. 1) with the trees emerging from the dynamics of randomly generated networks. In this way it is possible to investigate the structural and dynamical features of the suitable networks, possibly providing hypotheses on the generic properties of real networks.

Fig. 1.

Differentiation trees in intestinal crypts and hematopoietic cells. In (A) the crypt differentiation tree is shown, involving stem, transit amplifying stage (TA1, TA2-A, TA2-B), Paneth (PA), Goblet (GO), enteroendocrine (EE) and enterocyte (EC) cells [6]. In (B) the hematopoietic differentiation tree is shown, involving stem, multipotent progenitors (MPP), common myeloid progenitors (CMP), common lymphoid progenitors (CLP), megakaryocyte-erythroid progenitors (MEP), granulocyte-macrophage progenitors (GMP). The finally differentiate cells are considered only as distinct classes of differentiated cells (D1, D2, D3) [40].

This study is a part of a series of articles aimed at the analysis of the properties of the model of cell differentiation introduced in [39]. Other models have been proposed in course of the time, even if with distinct modeling approaches, e.g., [15, 17, 26].

In Sect. 2 the dynamical model of cell differentiation is described. In Sect. 3 the analyses concerning the topology, the dynamical regime and the lineage tree comparison are described. Section 4 the results of the simulations are shows, whereas Sect. 5 contains the final remarks.

2 A Dynamical Model of Cell Differentiation

Here we will briefly outline the main features of the dynamical model of cell differentiation introduced in [39], for a more exhaustive description please refer to the original work.

Random Boolean Networks (RBNs, [19–21]) are an abstract model of Gene Regulatory Network (GRN). These networks are directed graphs whose nodes are binary variables $x_i$ that model the activation/inactivation of the associated gene (i.e. production of a specific protein or RNA); the edges symbolize the regulatory paths. A Boolean updating function $f_i$ is associated to each $x_i$ and the update occurs synchronously at discrete time step for each node of the network, according to the value of the inputs nodes at the previous time step. So, if the state at time $t$ of a RBN is the binary vector $\mathbf{x }(t)$, the $i$-th component of state $\mathbf{x}(t+1)$ is:

$$\begin{aligned} \mathbf{x }(t+1)_i\mathop {\equiv }\limits ^{\text {def}}f_{i}(\mathbf{x }(t))\, \end{aligned}$$

(1)

Since the state-space is finite (i.e. there exist at most $2^{n}$ vectors in $\{0,1\}^n$) and the dynamics is fully deterministic, the system will end up in a limit cycle from any initial condition $\mathbf{x }(0)$ ⁴. Such a cycle is an attractor of the RBN and the sequence of states from $\mathbf{x }(0)$ to the cycle is the transient of the attractor; accordingly, the set of initial conditions ending up to the same attractor is named basin of attraction. Notice that attractors correspond then to gene activation patterns.

Considering that biological noise is known to play a role in several key cellular processes and in differentiation as well [4, 8, 12, 16, 18, 24, 25, 28, 37], an extension of RBNs accounting for stochastic fluctuations was developed, named Noisy Random Boolean Networks, NRBN [27, 31].

The key notion in the NRBN model, as presented in [39], is the definition of a attractor transition network (ATN). The ATN is a stability matrix whose entries represent the probability of switching among RBN attractors, as a consequence or random flips of the value of the nodes (i.e. $x_i=1$ gets flipped to $0$, and vice versa) in an attractor. From another perspective, the ATN describes the possibility of wandering among the attractors as a consequence of the smallest perturbation which can affect a RBN, i.e. the flip. In [31] we showed that the transition probability among attractors decreases sub-linearly with respect to the graph size.

Fig. 2.

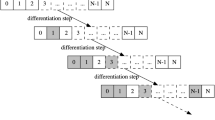
Example ATNs and TESs. An example of the threshold-dependent ATN and the corresponding tree-like TES landscape. The circle nodes are attractors of an example NRBN, the edges represent the relative frequency of transitions from one attractor to another one, after a 1 time step-flip of a random node in a random state of the attractor (performed an elevated number of times). In this case we show three different values of threshold, i.e.: $\delta = 0$, $\delta = 0.15$ and $\delta = 1$. TESs, i.e. strongly connected components in the threshold-dependent ATN with no outgoing links are represented through dotted lines and the relative threshold is indicated in the subscripted index. In the right diagram it is shown the tree-like representation of the TES landscape.

The definition of the ATN for a certain NRBN allows to represent the phenomenon of hierarchical stochastic differentiation. The underlying biological idea is the following: any cell type is characterize by a certain number of gene activation patterns in which the cell can wander as a consequence of random fluctuations and specific signals; besides, more differentiated cells are characterized by a better robustness against noise, because of more refined noise-control mechanism and, consequently, can roam in smaller portion of the state space, as experimentally proven by the higher level of noise in gene activation that has been detected in undifferentiated cells [10, 11, 13, 24].

In our model it possible to introduce a threshold $\delta \in [0,1]$ that is used to remove the transitions that are too rare, i.e. that cannot occur within the lifetime time of a cell, so defining a threshold dependent-ATN. Intuitively, higher thresholds represent better noise-control mechanism and are associated to progressively more differentiated cells. Each cell type of a cell is then associated to a so-called Threshold Ergodic Set (TES), as defined in [39]: given a certain threshold $\delta \in [0,1]$ a TES$_\delta$ is:

• a strongly connected component, SCC, in a threshold dependent-ATN,

• in which there are no outgoing links from any attractors belonging to the SCC toward an external attractor

TESs represent coherent stable ways of functioning of the same genome even in the presence of noise, i.e. cell types or modes. In this way, toti-/pluri-potent stem cells, for instance, will be characterized by a very low values of the threshold and will wander across various gene patterns, in order to resemble their biological capability of differentiating in various cellular types. Conversely, differentiated types will be associated to high thresholds. More in general, different thresholds will be associated to different degrees of differentiation. The phenomenon of stochastic differentiation is then defined as follows: the fate of a cell depends on the attractor where the cell is when the cell divides and the threshold increases. The new cell type will be that corresponding to the TES to which the attractor belongs in correspondence of the new threshold level. This allow to define parent and children types of cells and, accordingly, to draw a coherent a hierarchical differentiation tree. In principle, it is possible to map any desired differentiation tree to a partial order over thresholds (see Fig. 2).

Notice that in this case we intend to model only the stochastic differentiation process, whereas the model is capable of representing the deterministic differentiation as well⁵. Future analyses will investigate the repercussions of a change in the topology and in the dynamical regimes also with respect to it.

3 The Influence of Topology and of the Dynamical Regimes

The goal of the current work is to disentangle the effects of $(i)$ the topology and of $(ii)$ the dynamical regime of a NRBN on the properties of the TESs and, accordingly of the emerging differentiation tree. Considering that the information on real GRNs is still partial, along the lines of the complex systems approach we here focus on the generation of large ensembles of randomly generated networks with specific structural feature, in order to investigate the emergent dynamical properties of classes of networks and to relate them to the differentiation process.

Topological classes: random vs. scale-free. It was recently shown that genetic and metabolic networks might have a different topology than the Erdos-Renyi [9] one and, in particular, the presence of a large number of scarcely connected nodes and of a small number of largely connected nodes (i.e. the hubs) hints at the possible presence of an underlying power law in the distribution of the connections [3]. If $P(k)$ is the probability for a particular node of having $k$ connections, the power law is defined as:

$$\begin{aligned} P(k) = \frac{1}{Z}k^{-\gamma } \end{aligned}$$

(2)

$$\begin{aligned} Z=\sum _{i=1}^{k_{max}}i^{-\gamma } \end{aligned}$$

(3)

where $k$ can take values from $1$ to a maximum possible value $k_{max}= N - 1$ (self-coupling and multiple connections being prohibited). $Z$ coincides with the Riemann zeta function in the limit $k_{max} = \inf$ and is used as normalization factor; the parameter $\gamma$ is the scale-free exponent that characterizes the distribution. Variating $\gamma$ is possible to variate the pendency of the distributions, favoring the presence/absence of hubs. In this analysis we compare NRBNs built with a random topology of the connections (type $A$) with NRBNs with scale free topology (type $B$). The parameters of the simulations can be found in Table 1.

The dynamical regimes: ordered vs. critical vs. disordered. As specified in the introduction, it was analytically proven that by varying some key structural parameters of RBNs it is possible to characterize the emerging dynamical regime (on average). In particular, analytical studies presented in [2] on classical RBNs (with random topology) defined a phase diagram linking two structural parameters, the average connectivity and the so-called bias, a parameter that defines the likelihood of having a “1” output in the Boolean functions. In particular, a parameter $\lambda$, called sensitivity [59] or Derrida exponent, allows to discriminate the different dynamical regimes. If the Boolean functions are generated randomly with a bias $p$ and $A$ is the average connectivity of the network we have:

$$\begin{aligned} \lambda = 2Ap(1-p), \end{aligned}$$

(4)

Values of $\lambda$ smaller than 1 are typical of ordered networks, whereas values larger than 1 are characteristic of chaotic regime and the critical line at $\lambda = 1$ separate the two phases, indicating the critical region. The development of Eq. 4 for the critical case allows to draw a phase diagram regarding the dynamical regimes. In detail, for each value of $p$ there exist a critical value of the average connectivity $A$ such that the network is in the ordered regime for $A < A_{kr}(p)$ and in the chaotic regime for $A > A_{kr}$ The equation is the following:

$$\begin{aligned} A_{kr}=[2p(1-p)]^{-1} \end{aligned}$$

(5)

Extending the theory for RBNs with scale-free topology, as in [32], the critical $\gamma _{kr}$ for a network with $p= 0.5$ can be determined according to the following equation:

$$\begin{aligned} \frac{Z(\gamma _{kr}-1)}{Z(\gamma _{kr})}=2 \end{aligned}$$

(6)

Therefore we chose three parameters settings to design: ordered (type $1$), critical (type $2$), disordered (type $3$) NRBNs, with both the topologies. The parameters used in the simulations can be found in Table 1.

We here present the results of the analysis on 6 classes of NRBNs: random topology-ordered regime (type $A1$), random topology-critical regime(type $A2$), random topology-disordered regime (type $A3$), scale-free topology-ordered regime(type $B1$), scale-free topology-critical regime(type $B2$) and scale-free topology-disordered regime(type $B3$).

Tree matching. After generating random NRBNs satisfying the above mentioned parameters we compare the outcoming differentiation tree with the two real differentiation trees concerning intestinal crypts and hematopoietic cells in Fig. 1.

We associate totipotent stem cells with TESs at threshold $0$, cells in a pluripotent or multi-potent state (i.e. transit amplifying stage or intermediate state) with TESs with a larger threshold composed by one or more attractors, while completely differentiate cells to TESs with the highest threshold, usually composed by single attractors.

Given that each ATM can be characterizer by a high number of possible thresholds (i.e. all the distinct entries in the matrix), in order to reduce to computational costs, we do not check all the possible combination of thresholds in determining the outcoming tree. In particular, given an input tree of $Y$ levels, we define all the possible sets of $Y$ thresholds $\varDelta _x=[\delta _1, \delta _2, ..., \delta _Y], \delta _1 < \delta _2 <...< \delta _Y, \varDelta _x \subseteq [0, 0.01, 0.02, ..., 0.15]$. Given a certain ATM, every set of thresholds $\varDelta _x$ give rise to a specific tree, which is then compared with the target tree. We chose 0.15 as the maximum threshold value, because we observed that, on average, no further splitting of TESs is observed above that value (see the analyses below).

A measure of distance among the tree emerging from the NRBN dynamics and the real tree is defined as a sum of histogram distances for all the levels of the input tree [7]⁶. The larger this quantity is the more dissimilar the input and the emergent trees are. On the contrary when this quantity is zero it is not assured that the two trees completely match, but still it is a good quantitative approximation. Considered that, given a certain NRBN, many distinct trees are possible in correspondence of different sets of thresholds $\varDelta _x$, we compare the target tree with the emerging tree showing the minimum tree distance.

Notice that since the set of constraints we are imposing is non-trivial, we do not expect to find many “suitable” NRBNs.

Table 1. Parameters of the Noisy Random Boolean Networks.

4 Results

The first analyses regard the dynamical properties of the NRBNs in the 6 cases, with specific regard to the landscape and the properties of the TESs. Notice that in all the figures the left panel regard the random topology networks, the right panel the scale-free networks, the blue lines concern ordered networks, the red lines the critical networks and the green lines the disordered networks.

In Fig. 3 one can see the distribution of the number of distinct attractors in the 6 cases, the left panels corresponding to the random topology case (A1, A2, A3), the right panels to the scale-free case (B1, B2, B3)⁷.

Fig. 3.

Distribution of the number of distinct attractors. The distribution of the number of distinct attractors with respect to the 6 types of simulated networks is shown. The plot is in log-log scale and a box with the average value and the standard deviation of the number of distinct attractors is provided.

As expected, in NRBNs with random topology ordered networks are the most likely to have only one or a few attractors, disordered networks are the least likely to be in such situation, whereas critical networks are in between the two. Conversely, despite a very high dispersion, it interesting to notice that the average number of attractors is higher for critical networks, which are however known to display a very broad range of dynamical behaviors [5]. Scale-free NRBNs show a similar overall trend with regard to the proportion of networks with a low number of attractors, yet with smaller magnitudes and, above all, with smoother differences among the three cases, hinting at slighter dynamical differences among the regimes. Furthermore, the overall number of attractors is lower in the scale-free case than in the random case, which suggest that scale-free NRBNs with analogous parameters to random topology NRBNs are indeed more ordered. This result confirms those shown in [35].

The second analysis is aimed at disentangling the effect of topology and dynamical regime on the robustness of the attractors in presence of noise. In particular in Fig. 4 one can observe the distribution (and the average) of the values of the diagonal of the ATMs in the different cases, which provides an indication on how many times a NRBN, after a single-flip perturbation, returns to the same attractor.

It can be noticed that this indicator, with respect to both the topologies, reflects the level of robustness expected from the three dynamical regimes, with ordered networks being the most insensitive to perturbations (with typically higher probabilities to remain within the same attractor), disordered networks being instead the most sensitive to perturbations (with typically low probabilities to remain within the same attractors) and critical network showing intermediate behaviors. For what concerns the case of scale-free topology, although the same ranking holds, the behaviour of disordered and critical networks is closer to the behaviour of ordered networks with either random or scale-free topology. This outcome provides another evidence of the more ordered dynamical behaviour of scale-free networks when compared to random networks.

Less predictable is the likelihood of switching toward another given attractor, which is captured by non-null off-diagonal values. It is worth stressing that this indicator differs substantially from the probability to switch toward another attractor in general, which corresponds to the negative of the probability to remain in the same attractor (and include null off-diagonal values)). The frequency of these values for the 6 cases under study are plotted in Fig. 5. Interestingly, as long as the random topology is concerned, critical networks slightly move away from both the ordered and disordered regime (whose distributions mainly overlap) and show significantly low levels of probability to switch to a given attractor. This effect cannot be observed in the case of scale-free topologies where the differences between the three distributions are nearly negligible. This result may have important effects on the emerging lineage commitment tree. It is reminded that the differentiation is modeled as a gradual improvement of the noise-control mechanisms that hinder the transitions from undifferentiated to fully differentiated cells. It might be therefore the case that, even if the probability to exit from the current attractor (which corresponds to the probability to move to any other attractor) might be considerable, if the probability to reach another given attractor is typically low, this switch is more subject to be prevented by the noise control mechanism (which prevents switches that have probability below a threshold $\delta$).

Fig. 4.

Attractor stability (I). The distribution of the probability of remaining in the same attractor after a one-flip perturbation is shown, i.e. the distribution of the values of the diagonal of the ATN (bin = 0.01), w.r.t. the 6 classes of networks. In the box the average value is also shown.

This hypothesis can be investigated by analyzing the number of TESs, which in our model corresponds to different cell types, as a function of the threshold $\delta$. It can be indeed observed in Fig. 6 that the number of TESs of critical random network shows a steep increase in correspondence of a low $\delta$, moving away from both random ordered and random disordered networks, which exhibit a smoother increase and finally stabilize at significantly lower values. Notice also that the higher dispersion is observed in correspondence of critical network, which suggest a larger variability in the possible behaviors and, accordingly, of differentiation hierarchies. Consistently with the results regarding the probability to switch to a given attractor (Fig. 5), the differences in the three regimes are less clear in the case of scale-free topology, where the number of TESs is typically lower. Interestingly, in the latter case, the networks showing the maximum number of TES seem to be the disordered ones, which however show an average number of TES that is not even half of those of critical random networks.

Fig. 5.

Attractor stability (II). The distribution of the probability of switching from a random attractor toward another random attractor, i.e. the distribution of the non-zero off-diagonal values of the ATN (bin = 0.01) is shown with regard to the 6 typologies of networks. The x-axis is in log-scale, whereas in the box the average value is provided.

Fig. 6.

Variation of the number of TESs with respect to different thresholds. The average number (and the standard deviation) of the number of TESs with respect to the variation of the threshold $\delta$ in the range: $\delta \in [0: 0.01: 1]$ is shown, with regard to the 6 classes of networks.

Fig. 7.

Matching with intestinal crypt tree. In the upper panels the cumulative distribution of the minimum tree distances resulting from the comparison between the input differentiation tree of intestinal crypts (Fig. 1) and the suitable trees emerging from the NRBN dynamics is provided, with respect to the different classes of networks. Only a certain number of thresholds $\delta$ in the range: $\delta \in [0: 0.01: 1]$ is considered to compute the possible trees and for each network only the minimum distance on all the possible trees is considered. In the boxes the average values (and the standard deviation) of the distances are shown as well. In the lower panels the percentage of NRBNs that originate non-suitable trees for the comparison is shown such as, e.g., forests or trees with a number of nodes lower than the levels of the input trees.

Fig. 8.

Matching with hematopoietic cells tree. The comparison is made against the input hematopoietic cells differentiation tree (Fig. 1). See the previous caption for the description of the Figure.

Hence, it is possible to expect critical random network to have typically a considerable number of different cell types (TESs) at a given differentiation level (corresponding to a given threshold). It is therefore meaningful to investigate how similar the lineage tree emerging from these networks is to real ones, as compared to ordered or disordered networks. In this regard, in Figs. 7 and 8 one can observe the cumulative distribution of the tree distance, as defined in the previous section, with respect to the two lineage trees of Fig. 1, in the different cases. Because the tree distance can be calculated only when the obtained tree is comparable with the target one, that is, when it has at least the same depth, the fraction of NRBNs leading to at least one comparable tree is also shown in the figures (bottom panels).

Remarkably, regardless of the considered lineage tree (crypt or hematopoietic) and of the considered topology (scale-free or random) the probability to obtain a comparable tree is always maximum for disordered networks. It is worth noticing that the conditions that may affect the comparability of a tree are: (i) the number of attractors, which cannot be lower of the target tree’s depth; (ii) the possible existence of more than one TES at the level 0 (threshold 0) which would lead to a forest. According to the distribution probabilities in Fig. 3, disordered networks have the lowest probability to have a unique or a few attractor and therefore the lowest probability to have a tree with a smaller number of levels than the target trees.

The interpretation of the comparison of the distribution of the tree distances obtained in the comparable cases appears less straightforward. Let us first take into account the intestinal crypts differentiation tree (Fig. 7): it can be observed that the average distance does not highlight sharp differences between different dynamical regimes or topologies, and even when comparing the distribution it is difficult to tell which networks are actually performing better. Along similar lines, when the target is the hemopoietic cells tree, the differences in the six cases under study are nearly negligible. A non negligible difference can be observed only in the magnitude of standard deviations, which appears higher in random critical networks than in the other cases. The distribution of the distances regarding random critical nets shows indeed a long right tail, indicating that, in some cases, the tree emerging from these networks, despite having the same number of levels of the hemopoietic cells tree can differ substantially within each level. High distance values might be plausibly due to the typical higher number of TES observed in critical random nets.

It can however be noticed that the average distance in the intestinal crypt case (Fig. 7) is typically inferior to that of hematopoietic cells and that there is a non null probability to observe distance zero, which approximates a perfect match, in all the dynamical regimes and topologies considered. Although a distance equal to 0 is never observed in the case of hematopoietic cells tree (Fig. 8), it is however worth noticing that the a considerable fraction (the majority in case of scale-free topology) of the simulated networks can have a tree within a distance lower than 4, suggesting that the differentiation tree obtained from the sampled random networks is not that far from biologically plausible ones.

5 Conclusion

We have investigated the influence of the topology and of the dynamical regime of gene regulatory networks, as modeled with Noisy Random Boolean Network, with specific regard to the properties concerning cell differentiation. In particular, we have studied the properties of scale-free and random topology networks and in both cases we have analyzed ordered, critical and disordered networks. Remarkable differences were highlighted in the distinct cases.

First, the dynamical regime is strongly related to the stability of the attractors, suggesting that gene activation patterns in relatively more ordered networks are indeed more robust against random genomic mutations. Besides, scale-free networks appear to be generally more ordered, and hence robust, than analogous random-topology networks, so that even structurally disordered scale-free networks show behaviors that are comparable to ordered (or slightly subcritical) random networks.

A very interesting result is given by the average number and the dispersion of the number of TESs, which in our model represent cell types or modes. Random-topology critical networks show the larger average number and the highest variability, hinting at an intrinsic capability of critical network to show a great heterogeneity in the possible behaviors and, consequently, of possible emerging differentiation hierarchies. The hypothesis of criticality of gene networks was suggested by many and this could provide a further element in this direction. Conversely, and in accordance with the conclusions above, scale-free nets present a much ordered general behaviour, displaying a quite narrow range of possible behaviors, as given by the number and the variability of TESs.

The comparison with two real differentiation trees, i.e. intestinal crypts and hematopoietic cells, did not allow to achieve definitive conclusion on which network type is more suitable, even though slightly disordered networks display a larger number of comparable emerging trees, with respect to both the topologies. All in all, a surprisingly high portion of networks, across different dynamical regimes and topologies, originate trees that well approximate real ones, suggesting that rather simple differentiation schemes such those used in this study can be matched even through a random (not evolution-driven) generation. It is worth stressing that, as it has been previously observed (submitted work), networks in the slightly ordered regime can indeed exhibit behaviors that are more typical of the critical or disordered regime. Along similar lines critical or disordered dynamics can be observed in the slightly ordered regime. Hence, it could be interesting to investigate wether there exist some specific features shared by networks in the different regimes that can lead to the emergence of biologically plausible trees. Furthermore, the analysis of ensembles of networks evolved to fit the target trees (e.g. via bio-inspired algorithms) may unravel interesting new general properties.