Thermo-Elastic Simulation of Entire Machine Tool

Abstract

This paper presents an integrated approach to simulate the thermo-elastic behaviour of machine tools—from the CAD geometry data to FE modelling up to the thermo-elastic network model of variable structure that can be run in real time mode. The first part outlines the theoretical aspects of the methodology developed, whereas the second part demonstrates implementation in practice by means of concrete examples.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

7.1 Introduction

Thermo-elastic models that can be simulated for the overall system consisting of machine tool, process and environment are required for the design of compensation solutions, the evaluation of thermo-elastic behaviour and the correction of thermo-elastic errors during machine tool operation.

If it is important for the evaluation of the targeted design of the thermo-elastic behaviour in the design-oriented development phases to be carried out without real-time requirements to be fulfilled by the calculation algorithm, then the modelling, simulation and evaluation process can completely be executed at the FE system level. This approach is shown in the Chap. 6 in the same Lecture Notes.

Minimisation of calculation time is a key requirement for a quick analysis of a wide spectrum of thermal loads and boundary conditions and the correction of thermo-elastic errors during machine tool operation. Network-based modelling provides a solution: FE modelled machine tool (MT) assemblies without inner relative motions are transformed into compact objects by using model order reduction (MOR) method and are linked into a network model in a form of SIMULINK block diagram.

7.2 Approach

In purely thermo-elastic calculations, it is only necessary to take into account the static deformation effects, since the natural frequencies of the structural dynamics, which are significantly higher, are—as a rule—not excited by relatively slow thermal processes. For this reason, the so-called integration strategy of weak coupling is employed (Groth and Müller 2009; ANSYS 2014): in a first step, the temperature vector {T} is determined by means of numerical integration. In a second step, the problem of calculating the deformation vector {x} = f({T}) is solved as a quasi-static one on a possibly much rougher time scale.

This methodology makes it possible to divide the overall thermo-elastic problem into thermal transient and mechanical quasi-static subtasks. After discretization by means of FE method, both a system of differential Eq. (7.1a) and a system of linear Eq. (7.1b) of the following type are obtained

$$ [C_{T} ]\{ \dot{T}\} + [K_{T} ]\{ T\} = \{ \dot{Q}\} $$

(7.1a)

$$ [K]\{ x\} = \{ F\} - [K_{xT} ]\{ T\} \, $$

(7.1b)

with [C _T ], [K _T ], [K] and [K _xT ]—capacity, conductivity, mechanical stiffness and thermal stiffness matrices, {x} and {T}—the deformation and temperature vectors, {F} and {$\dot{Q}$}—mechanical and thermal load vectors.

The approach traced here is assembly-oriented. In this context, an assembly is a structural area with no internal relative motion. The assemblies, in turn, are connected to a network model by contact representations mapping the effect of large-sized relative motions like those typical for machine tools.

The associated modelling and calculation concept is illustrated in Fig. 7.1. The CAD models of machine structure are detailed in assemblies, from which thermal FE models are generated. The FE models are transformed into objects with substantially fewer degrees of freedom by means of model order reduction methods explained later. The contacts are led back to “external heat sources” mapping the heat exchange depending on the relative motion. Afterwards, the calculated vectors of the reduced degrees of freedom are retransformed into complete real assembly temperature vectors. The pose-specific deformation of the overall structure is finally determined by means of the pose-specific quasi-static Eq. (7.1b).

Fig. 7.1

Modeling and calculation concept

7.3 Results

7.3.1 Model Order Reduction

The Model Order Reduction (MOR) methods make it possible to efficiently generate compact model with good approximation properties directly from an original FE model (Schilders et al. 2000; Benner et al. 2005).

The approach starts with a formulation of the thermal subproblem as a state space representation that is entirely equivalent to the linear dynamic system (7.1a):

$$ \left\{ {\begin{array}{*{20}c} {u_{1} } \\ \vdots \\ {u_{k} } \\ \end{array} } \right\} \to \boxed{\Sigma :\begin{array}{*{20}c} {\{ \dot{T}\} + } \\ {} \\ \end{array} \begin{array}{*{20}c} {[A]\{ T\} } \\ {\{ y\} } \\ \end{array} \begin{array}{*{20}c} = \\ = \\ \end{array} \begin{array}{*{20}c} {[B]\{ u\} } \\ {[C]^{T} \{ T\} } \\ \end{array} } \to \left\{ {\begin{array}{*{20}c} {y_{1} } \\ \vdots \\ {y_{m} } \\ \end{array} } \right\} $$

(7.2)

The MOR method is applied to the thermal subproblem (7.1a) according to the conceptual design of the calculation, Fig. 7.1. For the transformation of the FE model (7.1a) in the form (7.2) see (Großmann et al. 2012b).

The input signals u _i are time-dependent parameters representing the loads applied to the FE model. The temperature vector {T} acts as the state vector in system (7.2). The system matrix [A] is determined by the geometry of the assembly to be modelled and its material parameters. Assuming that the thermal system is loaded by convection, the system matrix can be understood as the linear combination

$$ \left[ A \right] = \alpha_{1} \left[ {A_{1} } \right] + \cdots + \alpha_{s} \left[ {A_{s} } \right] $$

(7.3)

with heat transfer coefficients α _i . The control matrix [B] describes the location of the node positions of the loads the FE system is charged with. The output signals y _i map the state values that can be observed either as temperatures in selected FE nodes or as average temperatures over special ranges. The temperatures to be observed are chosen by means of the measurement matrix [C]. If [C] is defined as identity matrix, then this is the special case in which the original system (7.2) provides the overall temperature vector {T} as output signal vector {y}. The dimension N of the overall system Σ is defined by the dimension of the state vector {T}.

7.3.2 Structure and Parameter Preserving Krylov Model Order Reduction

A special type of MOR method was developed and employed. The basic idea of the method is that the original state vector is approximated in a Krylov subspace by means of its projection (Krylov 1931).

Let ${K}_{n} = span\{ \{ v_{1} \} , \ldots ,\{ v_{n} \} \} \subset {\mathbb{R}}^{N}$ be the subspace, and assume that n ≪ N and $\{ v_{1} \} , \ldots ,\{ v_{n} \}$ its orthonormal base. The matrix $\left[ {V_{n} } \right]\, = [v_{1} , \ldots ,v_{n} ]$is called the transformation matrix.

After insertion of the approximation $[V_{n} ]\{ \hat{T}\} = \hat{T}_{1} \{ v_{1} \} + \cdots + \hat{T}_{n} \{ v_{n} \}$ into system (7.2) thereby replacing the state vector {T} and later multiplication by the orthogonal matrix $[V_{n} ]^{T}$, the reduced system $\hat{\Sigma }$

$$ \left\{ {\begin{array}{*{20}c} {u_{1} } \\ \vdots \\ {u_{k} } \\ \end{array} } \right\} \to \boxed{\hat{\Sigma }:\begin{array}{*{20}c} {\{ \dot{\hat{T}}\} + } \\ {} \\ \end{array} \begin{array}{*{20}c} {[\hat{A}]\{ \hat{T}\} } \\ {\{ \hat{y}\} } \\ \end{array} \begin{array}{*{20}c} = \\ = \\ \end{array} \begin{array}{*{20}c} {[\hat{B}]\{ u\} } \\ {[\hat{C}]^{T} \{ \hat{T}\} } \\ \end{array} } \to \left\{ {\begin{array}{*{20}c} {\hat{y}_{1} } \\ \vdots \\ {\hat{y}_{m} } \\ \end{array} } \right\} $$

(7.4)

is generated from the original system $\Sigma$. In this equation, $\{ \hat{T}\}$ is the vector of the generalized coordinates related to the decomposition of {T} according to the base $\{ v_{1} \} , \ldots ,\{ v_{n} \}$ of the projection subspace K _n , and $[\hat{A}],[\hat{B}],[\hat{C}]$ defined as follows:

$$ \begin{aligned} \left[ {\hat{B}} \right] = \, \left[ {V_{n} } \right]^{T}\,\cdot\,\left[ B \right];\quad \left[ {\hat{C}} \right] & = \left[ {V_{n} } \right]^{T}\,\cdot\,\left[ C \right];\,\left[ {\hat{A}} \right] = \sum {\alpha_{l} \left[ {\hat{A}_{l} } \right]} \\ \text{with}\,\left[ {\hat{A}_{l} } \right] & = \left[ {V_{n} } \right]^{T}\,\cdot\,\left[ {A_{l} } \right]\,\cdot\,\left[ {V_{n} } \right] \\ \end{aligned} $$

(7.5)

The key task when designing the reduced model $\hat{\Sigma }$ from the original model $\Sigma$ is to obtain the transformation matrix [V _n ] or the Krylov subspace K _n .

The system $\Sigma$ is linear, so problem (7.2) can be expressed equivalently as given below:

$$ \Sigma :\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left\{ {\dot{T}_{1} } \right\} + \left( {\sum {\alpha_{l} \left[ {A_{l} } \right]} } \right)\left\{ {T_{1} } \right\} = u_{1} \left\{ {b_{1} } \right\}} & ; & {\left\{ {y_{1} } \right\} = \left[ C \right]^{T} \left\{ {T_{1} } \right\}} \\ \cdots & {} & \cdots \\ { \, \left\{ {\dot{T}_{k} } \right\} + \left( {\sum {\alpha_{l} \left[ {A_{l} } \right]} } \right)\left\{ {T_{k} } \right\} = u_{k} \left\{ {b_{k} } \right\}} & ; & {\left\{ {y_{k} } \right\} = \left[ C \right]^{T} \left\{ {T_{k} } \right\}} \\ \end{array} } \\ {\left\{ y \right\} = \left\{ {y_{1} } \right\} + \cdots \left\{ {y_{k} } \right\}} \\ \end{array} } \right. $$

(7.6)

where {b ₁ },…, {b _k } are the column vectors of the matrix [B].

The k first equations of (7.6) are subsystems of “single input signal” type and can each be handled by means of a classic Arnoldi process (Arnoldi 1951; Lohmann and Salimbahrami 2004; Großmann and Mühl 2010). In this case, the Arnoldi procedure explicitly provides the orthonormal base of the Krylov subspace. It should be mentioned that the parameter vector {α} = {α₁,…, α_s} is replaced by a 1-vector {1,…, 1} to build up the transformation matrices in the Arnoldi process.

$$ \begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left( {\sum {[A_{l} ]} } \right),\{ b_{1} \} : \, } & {\mathop \to \limits^{Arnoldi} } & {[V_{n}^{1} ]} \\ \end{array} } & {\mathop \to \limits^{(5)} } & {[\hat{A}_{l}^{1} ], \, \{ \hat{b}_{1} \} , \, [\hat{C}^{1} ]} \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots & {} & \cdots \\ \end{array} } & {} & \cdots \\ \end{array} } \\ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\left( {\sum {[A_{l} ]} } \right),\{ b_{k} \} : \, } & {\mathop \to \limits^{Arnoldi} } & {[V_{n}^{k} ]} \\ \end{array} } & {\mathop \to \limits^{(5)} } & {[\hat{A}_{l}^{k} ], \, \{ \hat{b}_{k} \} , \, [\hat{C}^{k} ]} \\ \end{array} } \\ \end{array} $$

(7.7)

Consequently, k reduced partial models ($\hat{\Sigma }_{1} , \ldots ,\hat{\Sigma }_{k}$) of the dimension n ≪ N are generated for k input signals of the original model Σ.

$$ \hat{\Sigma }:\left\{ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\hat{\Sigma }_{1} : \, \left\{ {\dot{\hat{T}}_{1} } \right\} + \left( {\sum {\alpha_{l} \left[ {A_{l}^{1} } \right]} } \right)\left\{ {\hat{T}_{1} } \right\} = u_{1} \left\{ {\hat{b}_{1} } \right\}} & ; & {\left\{ {\hat{y}_{1} } \right\} = \left[ {\hat{C}^{1} } \right]^{T} \left\{ {\hat{T}_{1} } \right\}} \\ \cdots & {} & \cdots \\ { \, \hat{\Sigma }_{k} : \, \left\{ {\dot{\hat{T}}_{k} } \right\} + \left( {\sum {\alpha_{l} \left[ {A_{l}^{1} } \right]} } \right)\left\{ {\hat{T}_{k} } \right\} = u_{k} \left\{ {\hat{b}_{k} } \right\}} & ; & {\left\{ {\hat{y}_{k} } \right\} = \left[ {\hat{C}^{k} } \right]^{T} \left\{ {\hat{T}_{k} } \right\}} \\ \end{array} } \\ {\left\{ {\hat{y}} \right\} = \left\{ {\hat{y}_{1} } \right\} + \cdots \left\{ {\hat{y}_{k} } \right\}} \\ \end{array} } \right. $$

(7.8)

The superposition of the output signal vectors of the partial models provides the approximation of the original model’s output signal vector (7.2).

Although it is impossible to a priori determine the accuracy of the MOR method, it was possible to successfully verify it in many practical examples. Selected validation experiments are described at the end of this paper.

At the end the following conclusions are derived:

• 1. The reduced model is of significantly smaller dimension in comparison with the unreduced FE original model if n ≪ N and can thus be calculated much more quickly.

• 2. The generation of the reduced model is independent of the specified input signals u _i and parameter values α _i .

• 3. The structure of the original system $\Sigma$ is explicitly preserved with the reduced system $\hat{\Sigma }$.

• 4. In the special case of the [C] identity matrix, the last equation of (7.8) provides the instructions to retransform the reduced temperature vector to the full temperature vector of the original FE model:

  $$ \left\{ T \right\} = \left[ {V_{n}^{1} } \right]\left\{ {\hat{T}_{1} } \right\} + \cdots + \left[ {V_{n}^{k} } \right]\left\{ {\hat{T}_{k} } \right\} $$

  (7.9)

In the thermal system, the time-dependent load parameters (such as heat flows and ambient temperatures) become a part of the input signal vector {u}, whereas the convective heat transfer coefficients become a part of the parameter vector {α}. For this reason, the points 2 and 3 given above mean that the generation of the compact reduced model from the original FE model is independent of the setting of the load parameters and can thus be carried out before parameter setting. Consequently, the one-time generated reduced model can be applied to different load distributions.

The structure preserving Krylov model order reduction method described above is called MOR-FE method in the following, since it is carried out immediately after the FE procedure thereby using the FE model as the original model for the MOR process, on the one hand. On the other hand, the outcomes obtained with the reduced calculation can be projected by retransformation to the original FE mesh to be used in, for instance, additional structural analyses in the FE domain or for visualisation purposes (compare Fig. 7.1).

7.3.3 Handling of Structural Variability

7.3.3.1 Thermal Model

Using the MOR-FE analysis described, a small-dimensional thermal model with load parameters standing for the inputs, as well as temperature values for the outputs, can be generated for each assembly (AS). The MOR-FEM-AS objects are the key elements of the network model created further on (compare Fig. 7.5).

The AS objects are coupled with other AS and environmental objects via contact-load conditions. These conditions in particular depend on the relative location of the contacting partners, and can be interpreted as movable heat sources from the view of a single AS object.

Structural variability in the thermal overall model is mapped as follows: at each point in time, the current location of the assemblies in relation to each other and to their ambient space is monitored. Each individual AS model’s load parameters depending on this location are calculated and transferred to the AS objects as inputs. Afterwards, state $\left\{ {\hat{T}_{BG} } \right\}$ is calculated on the individual AS models.

7.3.3.2 Mechanical Model

Having obtained the results of the numerical integration of the reduced thermal problem, the thermal state {$\hat{T}^{j}$} is known for each AS object j at the current point in time. Now we seek the deformation of the machine tool structure consisting of L assemblies in the time interval, in which the AS temperature does not change significantly.

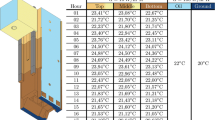
First it is possible to reproduce the temperature vector $\{ T^{j} \}$ for each AS and thus the temperature state $\left\{ T \right\} = \left\{ {\{ T^{1} \} , \ldots ,\{ T^{L} \} } \right\}$ of the overall machine tool (MT) structure by means of retransformation (7.9). The deformation {x} is found according to Eq. (7.1b) $\{ x\} = [K]^{ - 1} \{ F\} - [K]^{ - 1} [K_{xT} ]\{ T\}$, whereby the stiffness matrix and the thermal stiffness matrix depend on the assembly location relative to one to another (compare Fig. 7.2). The mutual arrangement of the AS (referred to as pose in the following), in turn, depends on the current TCP position in the workspace. As a result, deformation {x} is pose-specific.

Fig. 7.2

Pose dependency of the mechanical and thermal stiffness matrices on a hexapod MiniHex (compare Chap. 1); detailed to local positions of feed axes. Subdivision of the feed axis into four stationary assemblies (AS)

In the mechanical overall model, structural variability is considered as follows: a regular mesh of TCP supporting positions is placed over the workspace. A defined position of the MT structure exists for each of these discrete supporting positions (from 1 to M). The stiffness matrices $[K^{1} ], \ldots ,[K^{M} ]$ and the thermal stiffness matrices $[K_{xT}^{1} ], \ldots ,[K_{xT}^{M} ]$ are calculated previously and the deformation vectors $\{ x^{1} \} , \ldots ,\{ x^{M} \}$ are determined in real time by solving the simple system of linear Eq. (7.1b) only for these poses. The deformation in AS arrangements which are situated between the supporting positions is found via interpolation. This way full consistency with the correction model in subproject B07 (see Chap. 16) is achieved.

7.3.3.3 Thermo-Elastic Model

Distinguishing in the mechanical subproblem (7.1b) between subsystems that are independent of the temperature (7.10a) and those that are dependent on temperature (7.10b),

$$ \{ x\}_{static} = [K]^{ - 1} \{ F\} $$

(7.10a)

$$ \{ x\}_{therm} = - [K]^{ - 1} [K_{xT} ]\{ T\} $$

(7.10b)

$$ \{ x\} = \{ x\}_{static} + \{ x\}_{therm} $$

(7.10c)

we find that (7.10b) has a structure identical to that of the second equation of the state space representation of the thermal subproblem (7.2) (with $[C]^{T} = - [K]^{ - 1} [K_{xT} ]$). Thermal deformation $\{ x\}_{therm}$ can thus be understood as an additional output signal vector of the thermal problem.

More exactly it means the following:

Let j be the fixed pose and $[K^{j} ],\,[K_{xT}^{j} ]$ the related stiffness matrices. The complete MT structure consists of L assemblies so that the overall temperature vector {T} is composed of temperature vectors of single AS$\{ T\} = \left\{ {\{ T^{{BG_{1} }} \} , \ldots ,\{ T^{{BG_{L} }} \} } \right\}$. Consequently, the thermal deformation in position j can be expressed as superposition as follows (compare (7.10b))

$$ \{ x^{j} \}_{therm} = \underbrace {{\left[ { - [K^{j} ]^{ - 1} \,[K_{xT}^{j} ]} \right]_{{BG_{1} }} }}_{{[C_{x}^{{BG_{1} }} ]^{T} }}\{ T^{{BG_{1} }} \} + \cdots + \underbrace {{\left[ { - [K^{j} ]^{ - 1} \,[K_{xT}^{j} ]} \right]_{{BG_{L} }} }}_{{[C_{x}^{{BG_{L} }} ]^{T} }}\{ T^{{BG_{L} }} \} $$

(7.11)

where $\left[ { - [K^{j} ]^{ - 1} \,[K_{xT}^{j} ]} \right]_{{BG_{i} }} = [C_{x}^{{BG_{1} }} ]^{T}$ are the elements of the complete matrix $[K^{j} ]^{ - 1} \,[K_{xT}^{j} ]$ the i-th AS temperature affects. Expanding the thermal AS-related model (7.2) using the equation $\{ y_{x}^{{BG_{i} }} \} = [C_{x}^{{BG_{i} }} ]^{T} \{ T^{{BG_{i} }} \}$, the output signal vector $\{ y_{x}^{{BG_{i} }} \}$ provides the partial deformation of the MT structure. The superposition of these signal vectors over all of the assemblies supplies then the total thermal deformation $\{ x^{j} \}_{therm}$ in pose j.

The MOR method described above can be applied to the AS-related thermo-elastic original system $\Sigma_{x}$ extended this way

$$ \Sigma_{x} :\left\{ {\dot{T}} \right\} + \left[ A \right]\left\{ T \right\} = \left[ B \right]\left\{ u \right\}; \, \left\{ y \right\} = \left[ C \right]^{T} \left\{ T \right\}; \, \left\{ {y_{x} } \right\} = \left[ {C_{x} } \right]\left\{ T \right\} $$

(7.12)

The extended reduced system will include the identical set of transformation matrices (compare (7.7)), because the Arnoldi procedure remains independent of the additional measurement matrix [C _x ] in the Krylov MOR.

Depending on requirements of each application, two approaches to deformation calculation can be distinguished: deformation can be obtained by solving the mechanical subtask (7.1b) or (7.10a, 7.10b, 7.10c) by using the complete temperature vector {T} as input, whereby {T} is first calculated by the solution of the reduced thermal subtask $\hat{\Sigma }$ and subsequent retransformation by means of Eq. (7.9). An alternative is to interpret thermal deformation as an additional output signal of the thermal system (as described above). The extended reduced system $\hat{\Sigma }_{x}$ provides the approximation of this additional output signal.

The two approaches are identical in terms of accuracy. However, the second variant is more efficient in terms of the computational efforts, since the time-consuming retransformation step (compare (7.9)) is unnecessary. This extended thermo-elastic MOR-FEM is particularly efficient if only the displacement at the TCP, rather than the total deformation, is of interest, as it is, for instance, in the case of the correction application (compare Chap. 16).

7.3.4 Practice Implementation of the Approach Shown for a Ball Screw Axis

This section elucidates the step-wise application of the methods described above developed for a typical machine tool structure of a ball screw axis of a hexapod MiniHex (compare Fig. 7.2). Starting from the CAD model, a rapid network model in form of Simulink block diagram (see Fig. 7.5) is developed.

Step 1 CAD preparation: First, the complete MT structure has to be subdivided into assemblies (AS) without relevant inner relative motions, see Fig. 7.2. Further, the procedure is continued in an AS-oriented manner according to the approach (Fig. 7.1).

The AS geometry can be simplified by removing thermo-elastically irrelevant geometry details.

Remark: Such irrelevant geometry details are typically removed before the FE analysis. The reason is to obtain a model with a justifiable quantity of degrees of freedom (DoF) during meshing with non-degenerated finite elements. This quantity is proportional to the calculation time for the (unreduced) FE model. However, during MOR-FE analysis, the reduced model is used for calculation. Thanks to the MOR procedure, the reduced model’s DoF quantity is less by orders of magnitude. As a consequence, the mostly manual operation of geometry simplification no longer plays an important role, and can, under certain circumstances, even be omitted if appropriate automatic FE meshing tool is available.

Step 2 Thermal FE modelling: The AS geometry is imported into the FE software (for instance ANSYS), meshed, and the thermal material parameters (density, specific heat capacity and thermal conduction) are assigned. Then load types are applied to the AS—as a rule, on surfaces. Thereby convective loads and miscellaneous impressed heat flows are classified (compare Fig. 7.3).

Fig. 7.3

AS-oriented thermal FE modelling with prepared segmented spindle surface to enter position-dependent heat flows

A particular issue is the handling of surfaces through which heat flows are introduced depending on the relative AS position, such as spindle surfaces that are in frictional contact during the nut motion. These surfaces are cut into equidistant segments, see Fig. 7.3. One heat flow can be assigned to each segment. Thus it is possible to reconstruct the heat source motion, and thus it is completely consistent with the “local assignment” method in Chap. 16.

Ultimately, the matrices of the thermal FE model (7.2) are exported from ANSYS by means of in-house developed automatic ANSYS export routines (Großmann et al. 2011).

Step 3 Generation of Simulink-AS objects: A special library of “thermo-elastic network models” was developed and implemented (Fig. 7.4) for the block-oriented digital simulation (DBS) domain under Simulink. This library makes it possible to link the AS objects (block “AS”) mapped in a reduced way into the thermo-elastic network model, thereby considering the structural variability (compare Fig. 7.5).

Fig. 7.4

Blocks of the Simulink library “thermo-elastic network models”

Fig. 7.5

Network model of the ball screw based strut axis mapped as SIMULINK block diagram

When creating the AS block, the FE model exported from ANSYS is imported to Matlab/Simulink by using in-house developed routines and transformed into the reduced model by means of the MOR methods mentioned above.

Step 4 Insertion of control blocks: Special control blocks were developed for the library of “thermo-elastic network models”: a “temperature sensor” block makes it possible to define the ambient temperature (see Fig. 7.4); another sensor block, the “heat flow sensor”, provides defined heat flows as outputs.

An axis block represents a feed axis object returning typical axis process parameters, such as the motor torques of the axis drive, as well as the position and velocity in the axis coordinate system (compare Fig. 7.4).

Step 5 Initial positioning: At first, each AS has a local coordinate system (CS). For each AS object, the location of the local CS in the global CS is defined in relation to a “zero-AS arrangement” of the machine tool. Here the zero-AS arrangement means just the pose, in which the relative mutual position of the moved assemblies (AS) is zero. This is coherent to a {0, 0, 0}^T position in the machine coordinate system of an MT.

The positions of the sensor and axis objects in the global CS are specified analogously.

Step 6 Linking into a network model: The AS blocks are linked with each other and, if necessary, with the ambient (sensor) blocks by means of the contact blocks, see Fig. 7.5. The contact block represent a contact-load condition (compare Sect. 7.3.3 “Handling of structural variability”). Depending on the contact type, it is possible to choose among four contact blocks (compare Fig. 7.4).

Step 7 Parameter setting: The transient thermal calculation in the network model is carried out in the AS blocks at the level of reduced models. For this calculation, input signals, which are load parameters of the thermal model, are required. These load parameters are specified in the contact blocks. In the spindle-nut contact block, for instance, the heat flows for spindle and nut are each generated as functions of the axis parameters “position” and “velocity”. Heat conduction between spindle and nut is also considered, and the boundary temperatures of the frictional contact partners enter the heat flow calculation (compare Fig. 7.5).

The thermal network model is ready for simulation after step 7 when the input data (kinematic regime, external heat flows, ambient temperatures, etc.) are supplied.

If the network model is only supposed to be run “off-line”, then it is sufficient to supply input data captured by data logging from real or emulated operational scenarios.

For correction applications, however, the network model has to run “online” directly in the control of an MT. In this case, the input data are read out of the machine’s CNC during the operation in real time, and are transmitted to the network model. This variant was demonstrated successfully for the network model of the hexapod MiniHex at the technical exhibition SPS-IPC-Drives 2013 (Großmann et al. 2013) and at the 2nd Vienna Production Technology Congress (Großmann et al. 2014b). Details about the control core—model interface are described in Chap. 16.

Step 8 Mechanic FE modelling: For the extended thermo-elastic AS network model, the extended measurement matrix $[C_{x}^{{BG_{i} }} ]$ has to be generated according to Eq. (7.12) by means of the FE domain. For this purpose, the AS geometries meshed under step 2 are imported to ANSYS, where they are brought into the pose-specific AS arrangement and the mechanical material data and load parameters are assigned. Afterwards, the pose-dependent stiffness matrices $[K^{{Pose_{j} }} ],[K_{xT}^{{Pose_{j} }} ]$, as well as the static force vectors $\{ F^{{Pose_{j} }} \}$ are exported from ANSYS analogously to step 2. This process is repeated for each pose. For example, for a ball screw, the corresponding matrices are generated for two local poses (compare Fig. 7.2, right).

Step 9 Extension of the AS objects: Analogously to step 3, the mechanical part of the extended thermo-elastic model is imported to Matlab/Simulink and transformed into the reduced form.

Thermo-elastic extension means that the AS block has an additional output$\{ y_{x}^{{}} \}$. This vector consists of triples of part deformation in x, y and z. The superposition of these part deformations provides the thermal deformation at the TCP in the poses considered.

7.3.5 Calculation Results and Performance

The results are demonstrated for two typical MT structures. The first is a column-spindle head structure described in Großmann et al. (2012a) and in Galant (2013), see also Fig. 7.1. The second example is the ball screw based strut axis of the hexapod MiniHex (see Fig. 7.2).

7.3.5.1 ANSYS Versus Matlab/Simulink Calculation

The variable loads due to the movement of the spindle head were simulated on the machine column.

The outcomes of a comparison between a conventional unreduced calculation using ANSYS and the reduced network model calculation are summarised in Fig. 7.6. A more detailed explanation is given in Großmann et al. (2012a, b). The transient simulated temperatures of the unreduced original FE model and the reduced network model are almost congruent; whereby the reduced variant provides savings in computing time of several orders of magnitude (18,000 s. vs. 18 s.).

Fig. 7.6

Outcomes and performance of the unreduced and reduced models in comparison. Temperature (left) and displacement (right) in selected reference points

7.3.5.2 Simulation Versus Experiment: Column-Spindle Head

For the same column-spindle head structure, loads were simulated on the machine column investigated on a test bed with 13 switchable heating films for each guiding rail. The variable loads again resulted from spindle head movement. The test bed is depicted in detail in Großmann et al. (2014a) and in Chap. 21.

The comparison of measurement versus simulation of the reduced network model indicates only slight deviations, see Fig. 7.7.

Fig. 7.7

Column-spindle head structure: measured versus simulated temperatures by using the high-speed reduced model

7.3.5.3 Simulation Versus Experiment: Ball Screw Based Strut Axis

The reduced network model of the MiniHex was immediately implemented into the machine control and validated by measurements in cooperation with the subprojects B04, B07, C04 and C06. The comparison results for simulation versus measurement demonstrated by the temperatures of two strut axes at the same kinematic regime are illustrated in Fig. 7.8 and coincide significantly.

Fig. 7.8

Ball screw feed axis: measured temperatures versus temperatures obtained from simulations using the network model in real time

7.4 Classification Among the Objectives of the CRC/TR 96

The studies and research performed in the subproject A05 regarding the reduced thermo-elastic network model provide essential prerequisites for structure-variable modelling, particularly regarding the performance in terms of calculating time, permitting a structural model-based correction that explicitly represents the overall thermo-elastic functional chain to be implemented in the first place. For this reason, subproject A05 is closely aligned with subproject B07, which deals with structural model-based correction.

Expertise in parameter setting for power dissipations and heat transfers, mainly from the subprojects B04 and C04, is an additional contribution to the activities of subproject A05.

It is essential to validate the algorithms and models from A05 in experiment; this validation was conducted in cooperation with the work carried out in C06 and B07.

Ideas derived from subproject A06, especially regarding the parameter preserving model order reduction studied and developed in A06, were adopted and contributed to the network modelling algorithms.

7.5 Outlook

In the follow-up phases, the subproject A05 will retain its function as a lead project bringing together the partial models, as well as the technologies for modelling and parameter setting. Additional examples of machine tools will be explored, and the complexity of the associated network models is expected to increase significantly.