Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

3.1 Introduction

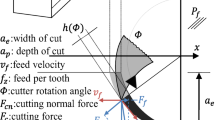
Metal cutting using a geometrically defined cutting edge is a highly sophisticated physical process. The cutting edge penetrates the part material until a critical shear stress value has been overcome. The surface layer removed is then moved across the tool’s rake surface. During the cutting process, most of the mechanical energy required is converted into thermal energy. Thus the metal cutting process is one of the main heat sources in a machine tool. The temperature distributions in the components involved in metal cutting—chip, part and tool—immediately affect the thermo-elastic deformation of tool and part holders, heat radiation into the machine tool’s interior and the metalworking fluid’s temperature. Consequently, the target of the subproject is the derivation of a heat flux distribution model based on parameters. In addition to the pure machining parameters, the parameters characterising different metal cutting processes and various combinations of part and tool materials, are also understood as parameters. The focus of the research is mainly on the milling process.

3.2 Approach

Fourier’s law of thermal conduction is used to determine heat flux through thermal conduction:

$$ q = - \lambda \frac{\partial T}{\partial n} $$
(3.1)

Heat flux q can thus be determined from thermal conductivity λ and the temperature gradient \( \partial {\rm T}/\partial {\text{n}} \) in each normal direction. Since it is impossible to measure the heat fluxes directly, the temperature fields appearing in the components of chip, tool and part during metal cutting are the key to the parameterised model that is sought. To derive the models for the temperature fields, in principal, it is possible to select empirical, analytical or simulation approaches. Empirical models are derived from measurements by means of regression without having to know the physical laws. In simulation and analytical models, these laws are taken into account in the solution to the thermal conduction differential equation. The thermal conduction differential equation can be presented in a generalised form as:

$$ \rho c\frac{\partial T}{\partial t} = \left[ {\frac{\partial }{\partial x}(\lambda \frac{\partial T}{\partial x}) + \frac{\partial }{\partial y}(\lambda \frac{\partial T}{\partial y}) + \frac{\partial }{\partial z}(\lambda \frac{\partial T}{\partial z})} \right] + \Phi $$
(3.2)

For constant thermal conductivity λ, it may be simplified to:

$$ \rho c\frac{\partial T}{\partial t} = \lambda \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial y^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) + \Phi $$
(3.3)

where ρ is the density, c is the specific heat capacity and Φ a term to take into account heat sources in the control volume. As a prerequisite to derive temperature fields for metal cutting, mainly milling, the derived analytical solutions must satisfy the differential equation.

3.3 Results

Prior to the formulation of parameter-based temperature distribution and heat flux models in the metal cutting process, potential analytical solutions Ψ are derived, see Fig. 3.1. These solutions are initially the mathematical solutions to (3.3) and depend not only on the spatial coordinates x and y, but also the model parameters (in Fig. 3.1 named as a, b, …).

Fig. 3.1
figure 1

Scientific approach for determination of heat flow

Full size image

Having adequately identified these model parameters, it is possible to derive temperature distributions during metal cutting T Model . The parameters in these distributions correspond to the cutting parameters (for instance, the cutting speed v c or the feed f). The modelled temperatures are validated by comparing them with the captured values T Mess using the temperature fields found experimentally. Only temperatures are measured rather than heat fluxes. For this reason, the heat flux field can only be validated indirectly. The heat fluxes are obtained from (3.1), differentiating the temperature field equation \( \partial T_{Model} /\partial n \) in the correspondingly chosen normal direction.

3.3.1 Derivation of Analytical Temperature Models in Metal Cutting

Since sensor access to the measured objects is limited, models predicting the temperatures during metal cutting were required very early on. Most of the existing models are empirical ones, and frequently the so-called heat partition coefficient describing the percentage of heat that flows in the tool and the chip is used. Empirical models do not have a physical basis, and it is impossible to predict entire temperature fields. Due to these weaknesses, this type of model is inflexible and difficult to transfer to new cases of application. In contrast, analytical models are based on the solution of the thermal conductivity differential equation and are thus regarded in principle as universal approaches. The model by Komanduri and Hou (2000, 2001a, b) whose approach uses an inclined band heat source, is the last model in this context and includes former models in a special solution. All models that have been provided up to now are based on real solutions of the thermal conductivity differential equation.

In the modelling performed in subproject A02, a potential theory-based model was made available. The potential theory provides methods for a complex solution of the thermal conductivity differential equation. The advantages in comparison with the state of the art result from the simultaneous modelling of the temperature field and the heat fluxes, as well as the flexible modelling opportunities following the tool-kit principle. Using the methodology shown in Fig. 3.1, it is possible to derive a solution for the temperature field in metal cutting. The following complex function is obtained:

$$ \begin{aligned} F(z) & = F_{uniform} + F_{vortex} + F_{corner} \\ & = Aze^{ - i\alpha } + \frac{Bi}{2\pi }\ln (z + z_{sum} ) + C \cdot z_{rot}^{k} \\ \end{aligned} $$
(3.4)

The function is superpositioned from the partial solutions F uniform , F vortex and F corner . Each function can be assigned a physical interpretation analogously to fluid mechanics, which need not be detailed here. For a detailed derivation, see Gierlings and Brockmann (2013). The imaginary part Ψ, which can be interpreted as a function for the temperature field according to the methodology in Fig. 3.1, is given as:

$$ \begin{aligned} \Psi_{total} (x,y) & = A\sin (\alpha ) - \frac{B}{2\pi }\ln (\sqrt {x_{total}^{2} + y_{total}^{2} } ) \\ & \quad + C \cdot [\sqrt {(x\cos \theta - y\sin \theta )^{2} + (x\sin \theta + y\cos \theta )^{2} } ]^{k} \sin (k\theta ) \\ \end{aligned} $$
(3.5)

The parameters A, α, B, C, θ and k can be regarded as constants.

The terms x total and y total are introduced to take into account the heat sources from friction and shearing. Figure 3.2 presents a plot of the calculated temperature field as well as of an exemplary temperature curve along the contact zone. To validate the temperature fields measured, the temperature fields are compared with the measurements. The direct relationship between the solution parameters and the cutting parameters was not determined in the project activities demonstrated; the parameters were chosen so that the qualitative curve of the temperature fields conforms.

Fig. 3.2
figure 2

Model plot and temperature along the contact zone

Full size image

3.3.2 Measurement of Temperature Fields in Metal Cutting

Different commonly available temperature sensor systems were engineered for a metal cutting application to capture temperatures in the metal cutting process. First, indirect measurement techniques and techniques with time-resolution can be distinguished. Indirect measurements, such as the use of temperature-sensitive colours or of powders with a constant melting point, as well as the estimation of metallurgical microsections, are not feasible as temperature measurement techniques applied to science and industry.

The more suitable time-resolved measurement methods, in turn, can be subdivided into thermo-electrical techniques and radiation measurement procedures. Resistance thermometers and thermocouples belong to the first type. These measurement methods were not employed in the subproject, since they are inappropriate for exact measurement of temperature fields in short measurement times.

The thermographic and pyrometric principles categorized as radiation measurement, offer the strength of contactless measurement, which can be distinctly advantageous in metal cutting investigations. Thermographic cameras are capable of recording a complete temperature image, with which it is possible to draw conclusions about a complete temperature field in a single measurement. One disadvantage of the camera technologies currently available, however, is that emissivity of metals, which, in turn, depends on wave length and temperature, is unknown. A real remedy is provided by two-colour pyrometry, based on—in contrast to thermography—the measurement of radiation at two discrete wavelengths. A suitable wavelength selection can allow for a change in emissivity to be neglected to a certain degree and thus guarantee absolute temperature measurement. However, a weakness of this technique is that the measurement is only conducted at one measuring point.

To combine the strengths of the two radiation measurement techniques, an online emissivity calibration method was engineered in the subproject: a spot on the test object is recorded by both sensor systems at the same time. Thus it is possible to compare the digital level of the infrared (IR) camera with the temperature recorded by means of the two-colour pyrometer and use the outcomes for emissivity determination; compare with the diagram in Fig. 3.3.

Fig. 3.3
figure 3

Methodology for online emissivity calibration

Full size image

Since the image rate is limited and dependent on the integration time, it is necessary to specify the location of the common measurement spot in the metal cutting zone. This is especially valid for the zones shown in the IR camera image—rake face, contact zone, chip and chip underside; see upper part of Fig. 3.3. By adjusting the IR images calibrated in the abovementioned manner, model validation by means of accurate measured data can be guaranteed.

3.3.3 Equation for the Heat Flux

To derive the heat flux model based on parameters from the temperature models, it is first necessary to derive the direction of the heat flux. According to (3.1), heat flux is to be determined in the corresponding normal direction. In other words, the field is perpendicular to the isothermals determined by (3.5). Since the equation was derived from a potential function \( F\left( z \right) = \Phi + {\text{i}}\Psi \), the real and imaginary parts of the function are in a mutually vertical position (except in singular points in which the Cauchy-Riemann conditions are not fulfilled). Consequently, the heat flux resulting from the real part Φ of (3.5) is given as:

$$ \begin{aligned} \Phi & {\text{ = Acos(}}\alpha )+ \frac{\text{B}}{ 2\pi }\tan^{ - 1} (\frac{{y_{total} }}{{x_{total} }}) \\ & \quad + C[\sqrt {(x\cos (\theta ) - y\sin (\theta )^{2} + (x\sin (\theta ) + y\sin (\theta )^{2} } ]^{k} \cos (k\theta ) \\ \end{aligned} $$
(3.6)

The meaning of the parameters is identical with those in (3.5). The strength of the heat flux results from the gradient in the direction of this field. Figure 3.4 elucidates the geometric relationships between the isothermal and the heat flux.

Fig. 3.4
figure 4

Heat source field and direction

Full size image

The heat fluxes in x and y directions can be derived from the corresponding derivatives of the Ψ function. To calculate heat flux into the components, heat flux is multiplied by the area considered.

3.4 Classification of Outcomes CRC/TR 96

Parameter-based modelling of the temperature field induced by the metal cutting process is a key parameter for compensation and correction solutions.

The tool holder and part clamping components are immediately affected by the heat flux out of the metal cutting process. Heat is mainly transmitted via contact grooves between tool and tool holder as well as between part and part clamping. The machine interior is also affected directly by heat radiation, which is, in turn, dependent on the temperature of the component’s chip, tool and part. The cooling lubricant that is available in most metal-cutting processes is also heated by convection and thus changes the temperature in the hydraulic circuit. As a whole, complex process representation is created, showing the tool and the part interacting with the cutting process as the heat source to be characterized by parameters (that is, to be changed by cutting parameters, such as cutting speed and feed).

This representation can be employed for process optimisation, on the one hand. On the other hand, the models can be used for specific relationships between energy input and accuracy curves as a function of productivity. In this way, they provide technological support for the overall system of the CRC/TR 96.

3.5 Outlook

The model to predict the temperature fields in the components of tool, part and chip engineered in the subproject A02 needs to be further developed in the ongoing subproject activities. In a first step, the relationship to the cutting parameters is generated explicitly in order to assess the models according to the productivity axis. In a second step, the model is expanded to more general chip geometries and cases of application. This is guaranteed by a method for the application of elementary solutions. Analogously to fluid mechanics, this paradigm is known as panel theory. Initially, the model can only be used for stationary cases in concrete applications. The intention is to extend the approach to unsteady cases by means of the theory of minor disturbances.