Keywords

1 Introduction, the State Feedback (SF)

It is a well known methodology to use the state variable representations (SVR) of linear time invariant (LTI) single input - single output (SISO) systems [1]. The SVR proved to be excellent tool to implement both LQR (Linear system - Quadratic criterion - Regulator) control and pole placement design. The practical applicability required to introduce the observers, which make this methodology widely applied even for large scale and higher dimension plants [3]. Thousands of theoretical considerations mostly concentrate on the irregularities and special structures in the SVR appearing and much less publications deal with the model error properties of these systems.

It is possible to find a proper new way to discuss and investigate the the special properties and limitations of the classical state-feedback (SF), state-feedback/observer (SFO) topologies if someone replaces the SVR by their transfer function representations (TFR) [2].

Consider a SISO continuous time (t) LTI dynamic plant described by the SVR

$$ P=\frac{B}{A} $$
(1)

Here P is the TFR of the open-loop system with the numerator and denominator polynomials

$$ B(s)={s}^n+{b}_1{s}^{n-1}+\cdots +{b}_{n-1} s+{b}_n $$
(2)
$$ A(s)={s}^n+{a}_1{s}^{n-1}+\cdots +{a}_{n-1} s+{a}_n $$
(3)

If we want to express the operation of the SF by equivalent scheme using TFR forms, Fig. 1 can be used, where the feedback regulator R f = K k is obtained from the basic equation (complementary sensitivity function, CSF) of the closed-loop

$$ {T}_{\mathrm{r}\mathrm{y}}(s)=\frac{k_{\mathrm{r}}\kern2.77695pt B(s)}{R(s)}=\frac{k_{\mathrm{r}}\kern2.77695pt B(s)}{A(s)+ K(s)}=\frac{k_{\mathrm{r}}\kern2.77695pt P}{1+{K}_k\kern2.77695pt P} $$
(4)
Fig. 1
figure 1

Equivalent schemes of SF using TFR forms

Full size image

where k r is obtained by requiring that the static gain of T ry should be equal to one. The calibrating factor k r is necessary because the closed-loop using SF is not an integrating one. Equation (4) clearly shows, that the open-loop zeros remain unchanged and the closed-loop poles will be the required ones. The solution formally makes the characteristic polynomial of the closed-loop equal to the desired polynomial ("placed poles")

$$ R(s)={s}^n+{r}_1{s}^{n-1}+\cdots +{r}_{n-1} s+{r}_n $$
(5)

Here it is obtained that

$$ {R}_{\mathrm{f}}={K}_k(s)=\frac{K(s)}{B(s)}=\frac{R(s)- A(s)}{B(s)} $$
(6)

which corresponds to the state feedback vector in the classical SVR.

2 Observer-Based State-Feedback with Equivalent TFR Forms

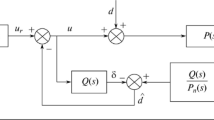
The practical applicability of the SF theory was introduced by the development of the observers capable to calculate the unmeasured state variables. The most general SF/Observer (SFO) topology discussed above can also be given using equivalent TFR forms of SF and is shown in Fig. 2.

Fig. 2
figure 2

Equivalent topology of the general basic SFO scheme using TFR forms

Full size image

The usual classical design goal for the observer is to determine the observer feedback so that its feedback closed-loop system has the characteristic polynomial

$$ Q(s)={s}^n+{q}_1{s}^{n-1}+\cdots +{q}_{n-1} s+{q}_n $$
(7)

The TFR K l (s) = L(s)/B(s) in Fig. 2 corresponds to the observer feedback vector in the classical SVR.

The pole-placement design goals for the SF and observer dynamics require

$$ k(s)= R(s)- A(s)\kern1em a n d\kern1em L(s)= Q(s)- A(s) $$
(8)

After some long, but straightforward block manipulations the equivalent SFO scheme can be transformed into another unity feedback closed-loop form given in Fig. 3.

Fig. 3
figure 3

Reduced equivalent topology of the general basic SFO scheme

Full size image

It is interesting to observe that the transfer function of the closed-loop in Fig. 3 has a very special structure

$$ \frac{P^2{K}_k{K}_l}{1+ P\left({K}_k+{K}_l\right)+{P}^2{K}_k{K}_l}=\frac{P{K}_k}{1+ P{K}_k}\frac{P{K}_l}{1+ P{K}_l}=\frac{K}{R}\frac{L}{Q} $$
(9)

It is formally two simpler closed-loops cascaded, which dynamically completely corresponds to the characteristic equation: R(s) = 0 and Q(s) = 0. The overall transfer function of the SFO system is

$$ {T}_{\mathrm{r}\mathrm{y}}(s)={k}_{\mathrm{r}}\frac{1+ P{K}_l}{P{K}_k{K}_l}\frac{P{K}_k}{1+ P{K}_k}\frac{P{K}_l}{1+ P{K}_l}=\frac{k_{\mathrm{r}} P}{1+ P{K}_k}=\frac{k_{\mathrm{r}} B}{R} $$
(10)

3 Model Error Properties

The above widely applied methodology has a common problem, that in all regulator and observer equations the true process P is used instead of the estimated model \( \hat{P} \) of the process. The equivalent TFR form of the SF using the model of the process is shown in Fig. 4.

Fig. 4
figure 4

The model based SF scheme and error

Full size image

The parallel scheme in Fig. 4 is used to compute the model error. Using (4) the \( {\hat{T}}_{\mathrm{ry}} \) model-based version of T ry is

$$ {\hat{T}}_{\mathrm{r}\mathrm{y}}=\frac{k_{\mathrm{r}}\kern2.77695pt P}{1+{K}_k\kern2.77695pt \hat{P}}=\frac{k_{\mathrm{r}} B}{R}\frac{\hat{A}}{A}={T}_{\mathrm{r}\mathrm{y}}\frac{\hat{A}}{A}\hat{A} $$
(11)

and its relative uncertainty

$$ {\ell}_{\mathrm{T}}=\frac{{\hat{T}}_{\mathrm{ry}}-{T}_{\mathrm{ry}}}{{\hat{T}}_{\mathrm{ry}}}=\frac{\hat{A}- A}{A}={\ell}_A $$
(12)

which shows that ℓ T = 0 for ℓ A  = 0. Introducing the additive \( \varDelta = P-\hat{P} \) and relative plant model error

$$ \ell =\frac{\varDelta}{\hat{P}}=\frac{P-\hat{P}}{\hat{P}} $$
(13)

the modeling error ε k in Fig. 4 can be expressed as

$$ {\varepsilon}_k=\frac{k_{\mathrm{r}}\hat{B}}{B}\ell \kern2.77695pt r={T}_{\mathrm{r}\mathrm{y}}\frac{\hat{B}}{B}\kern2.77695pt \ell \kern2.77695pt r=\hat{P}\kern2.77695pt \ell \kern2.77695pt u $$
(14)

The SFO scheme is widely applied in the practice with model-based SVR, so it is interesting how the model-based scheme in Fig. 5 influences the original modeling error ε k .

Fig. 5
figure 5

Model based SFO scheme with TFR forms

Full size image

After some long but straightforward computations

$$ {\varepsilon}_l=\frac{\hat{P}}{1+{K}_l\hat{P}}\kern2.77695pt \ell \kern2.77695pt u=\frac{\hat{B}}{Q}\ell \kern2.77695pt u=\frac{1}{1+{K}_l\hat{P}}{\varepsilon}_k $$
(15)

is obtained. Equation (15) clearly shows the influence of the SFO scheme, because it decreases the modeling error ε k by (\( 1+{K}_l\hat{P} \)). Selecting fast observer poles, one can reach quite small "virtual" modeling error ε l in the major frequency domains of the tracking task.

Besides the radical model error attenuating behavior of the model-based SFO scheme, unfortunately it has a very important drawback, the nice cascade (9) structure changes to

$$ {\left.\frac{{\hat{P}}^2{K}_k{K}_l\left(1+\ell \right)}{1+\hat{P}\left({K}_k+{K}_l\right)+{\hat{P}}^2{K}_k{K}_l\left(1+\ell \right)}\right|}_{\ell \to 0}=\frac{P{K}_k}{1+ P{K}_k}\frac{P{K}_l}{1+ P{K}_l}=\frac{K}{R}\frac{L}{Q} $$
(16)

which form is not factorable except for the exact model matching case, when ℓ → 0. On the basis of Fig. 5 and (16) it is easy to see that the poles of the observer feedback loop remain unchanged using the placement design equation forms model-based SFO (8), thus the only solution is to use the available model of the process, in this case \( \hat{A} \), i.e.,

$$ K(s)= R(s)-\hat{A}(s)\kern1em \mathrm{a}\mathrm{n}\mathrm{d}\kern1em L(s)= Q(s)-\hat{A}(s) $$
(17)

for the pole placing equations.

Because this design ensures the required poles only for small ℓ (see (16)), a serious robust stability investigation is required first. Next it is important to investigate where the actual pole is located for non zero ℓ, so how big the performance loss is coming from the model based SFR. These steps are usually neglected in most of the published papers, books and applications.

4 Introducing the Observer Based Y oula-Regulator

For open-loop stable processes the all realizable stabilizing (ARS) model based regulator \( \hat{C} \) is the Y oula -parametrized one:

$$ \hat{C}\left(\hat{P}\right)={\left.\frac{Q}{1- Q\hat{P}}\right|}_{\hat{P}\to P}=\frac{Q}{1- Q P}= C(P) $$
(18)

where the "parameter" Q ranges over all proper (Q(ω = ∞) is finite), stable transfer functions [5], [6], see Fig. 6a.

Fig. 6
figure 6

The equivalent IMC structure of an ARS regulator

Full size image

It is important to know that the Y-parametrized closed-loop with the ARS regulator is equivalent to the well-known form of the so-called I nternal M odel C ontrol (IMC) principle [6] based structure shown in Fig. 6b.

Q is anyway the transfer function from r to u and the CSF of the whole closed-loop for \( \hat{P}= P \), when ℓ → 0

$$ {\hat{T}}_{\mathrm{ry}}=\frac{\hat{C} P}{1+\hat{C} P}= Q P{\left.\frac{1+\ell }{1+\left(1- QP\right)\ell}\right|}_{\ell \to 0}= Q P={T}_{\mathrm{ry}} $$
(19)

is linear (and hence convex) in Q.

It is interesting to compute the relative error ℓ T of \( {\hat{T}}_{\mathrm{ry}} \)

$$\begin{array}{ll}{\ell}_{\mathrm{T}}&=\frac{T_{\mathrm{ry}}-{\hat{T}}_{\mathrm{ry}}}{{\hat{T}}_{\mathrm{ry}}}=\frac{T_{\mathrm{ry}}}{{\hat{T}}_{\mathrm{ry}}}-1= Q\left( P-\hat{P}\right)= Q P\frac{\ell }{1+\ell }\\&={T}_{\mathrm{ry}}\frac{\ell }{1+\ell } \end{array}$$
(20)

The equivalent IMC structure performs the feedback from the model error ε Q . Similarly to the SFO scheme it is possible to construct an internal closed-loop, which virtually reduces the model error to

$$\begin{array}{ll} {\varepsilon}_l&=\frac{1}{1+{\hat{K}}_l\hat{P}}\left( y-\hat{P} u\right)=\frac{1}{1+{\hat{K}}_l\hat{P}}{\varepsilon}_Q=\frac{1}{1+{\hat{L}}_l}{\varepsilon}_Q \\&=\hat{H}\kern2.77695pt {\varepsilon}_Q\kern1em ;\kern1em {\hat{L}}_l={\hat{K}}_l\hat{P} \end{array}$$
(21)

and performs the feedback from ε l (see Fig. 7), where \( {\hat{L}}_l \) is the internal loop transfer function. In this case the resulting closed-loop will change to the scheme shown in Fig. 8.

Fig. 7
figure 7

The observer-based IMC structure

Full size image
Fig. 8
figure 8

Equivalent closed-loop for the observer-based IMC structure

Full size image

This means that the introduction of the observer feedback changes the Y oula -parametrized regulator to

$$ {\hat{C}}^{\prime}\left({\hat{P}}^{\prime}\right)=\frac{Q}{1- Q\hat{P}/ \left(1+{\hat{K}}_l\hat{P}\right)}=\frac{Q\left(1+{\hat{K}}_l\hat{P}\right)}{1+{\hat{K}}_l\hat{P}- Q\hat{P}} $$
(22)

The form of \( {\hat{C}}^{\prime } \) shows that the regulator virtually controls a fictitious plant \( {\hat{P}}^{\prime } \) which is also demonstrated in Fig. 8. Here the fictitious plant is

$$ {\hat{P}}^{\prime }=\frac{\hat{P}}{1+{\hat{K}}_l\hat{P}}=\frac{\hat{P}}{1+{\hat{L}}_l} $$
(23)

The closed-loop transfer function is now

$$\begin{array} {ll}{\hat{T}}_{\mathrm{ry}}^{\prime }&=\frac{{\hat{C}}^{\prime } P}{1+{\hat{C}}^{\prime } P}=\frac{QP\left(1+{\hat{K}}_l\hat{P}\right)}{1+{\hat{K}}_l\hat{P}- Q\hat{P}+ QP}\\&={\left. QP\frac{1}{1+ QP\frac{1}{1+{\hat{K}}_l\hat{P}}\kern2.77695pt \frac{\ell }{1+\ell }}\right|}_{\ell \to 0}= Q P={T}_{\mathrm{ry}} \end{array}$$
(24)

The relative error ℓ ′T of \( {\hat{T}}_{\mathrm{ry}}^{\prime } \) becomes

$$ {\ell}_{\mathrm{T}}^{\prime }=\frac{T_{\mathrm{ry}}-{\hat{T}}_{\mathrm{ry}}^{\prime }}{{\hat{T}}_{\mathrm{ry}}^{\prime }}=\frac{T_{\mathrm{ry}}}{{\hat{T}}_{\mathrm{ry}}^{\prime }}-1= Q P\frac{\ell }{1+\ell}\frac{1}{\left(1+{\hat{K}}_l\hat{P}\right)}={\ell}_{\mathrm{T}}\frac{1}{1+{\hat{L}}_l} $$
(25)

which is smaller than ℓ T. The reduction is by \( \hat{H}=1 / \left(1+{\hat{L}}_l\right) \).

5 An Observer Based PID-Regulator

The ideal form of a Youla-regulator based on reference model design [4], [5] is

$$ {C}_{id}=\frac{\left({R}_n{P}^{-1}\right)}{1-\left({R}_n{P}^{-1}\right) P}=\frac{Q}{1- QP}=\frac{R_n}{1-{R}_n}{P}^{-1} $$
(26)

when the inverse of the process is realizable and stable. Here the operation of R n can be considered a reference model (desired system dynamics). It is generally required that the reference model has to be strictly proper with unit static gain, i.e., R n(ω = 0) = 1.

For a simple, but robust PID regulator design method assume that the process can be well approximated by its two major time constants, i.e.,

$$ P\cong \frac{A}{A_2}\kern1em \mathrm{w}\mathrm{h}\mathrm{e}\mathrm{r}\mathrm{e}\kern1em {A}_2=\left(1+ s{T}_1\right)\left(1+ s{T}_2\right) $$
(27)

According to (26) the ideal Youla-regulator is

$$ {C}_{\mathrm{id}}=\frac{R_{\mathrm{n}}{P}^{-1}}{1-{R}_{\mathrm{n}}}=\frac{R_{\mathrm{n}}\left(1+ s{T}_1\right)\left(1+ s{T}_2\right)}{A\kern2.77695pt \left(1-{R}_{\mathrm{n}}\right)}\kern1em ;\kern1em {T}_1>{T}_2 $$
(28)

Let the reference model R n be of first order

$$ {R}_{\mathrm{n}}=\frac{1}{1+ s{T}_{\mathrm{n}}} $$

which means that the first term of the regulator is an integrator

$$ \frac{R_{\mathrm{n}}}{1-{R}_{\mathrm{n}}}=\frac{1/ \left(1+ s{T}_{\mathrm{n}}\right)}{1-1/ \left(1+ s{T}_{\mathrm{n}}\right)}=\frac{1}{1+ s{T}_{\mathrm{n}}-1}=\frac{1}{s{T}_{\mathrm{n}}} $$
(29)

whose integrating time is equal to the time constant of the reference model. Thus the resulting regulator corresponds to the design principle, i.e., it is an ideal PID regulator

$$ {C}_{{PID}}={A}_{{PID}}\frac{\left(1+ s{T}_{{I}}\right)\left(1+ s{T}_{{D}}\right)}{s{T}_{{I}}}={A}_{{PID}}\frac{\left(1+ s{T}_1\right)\left(1+ s{T}_2\right)}{s{T}_1} $$
(30)

with

$$ {A}_{{PID}}={T}_1/ A{T}_{{n}}\kern1em ;\kern1em {T}_{{I}}={T}_1\kern1em ;\kern1em {T}_{{D}}={T}_2 $$
(32)

The Youla-parameter Q in the ideal regulator is

$$ Q={R}_{{n}}{P}^{-1}=\frac{1}{A}\frac{\left(1+ s{T}_1\right)\left(1+ s{T}_2\right)}{1+ s{T}_{{n}}} $$
(33)

It is not necessary, but desirable to ensure the realizability, i.e., to use

$$ Q={R}_{{n}}{P}^{-1}=\frac{1}{A}\frac{\left(1+ s{T}_1\right)\left(1+ s{T}_2\right)}{\left(1+ s{T}_{{n}}\right)\left(1+ s T\right)} $$
(34)

where T can be considered the time constant of the derivative action (0.1 T D ≤ T ≤ 0.5 T D). The regulator \( {\hat{C}}^{\prime } \) and the feedback term \( \hat{H} \) must be always realizable. In the practice the PID regulator and the Youla-parameter is always model-based, so

$$ {\hat{C}}_{{PID}}\left(\hat{P}\right)={\hat{A}}_{{PID}}\frac{\left(1+ s{\hat{T}}_1\right)\left(1+ s{\hat{T}}_2\right)}{s{\hat{T}}_1}\kern1em ;\kern1em {\hat{A}}_{{PID}}=\frac{{\hat{T}}_1}{\hat{A}\kern2.77695pt {T}_{{n}}} $$
(35)
$$ \hat{Q}={R}_{{n}}{\hat{P}}^{-1}=\frac{1}{\hat{A}}\frac{\left(1+ s{\hat{T}}_1\right)\left(1+ s{\hat{T}}_2\right)}{1+ s{T}_{{n}}} $$
(36)

The sheme of the observer based PID regulator is shown in Fig. 9, where a simple PI regulator

$$ {\hat{K}}_l={A}_l\frac{1+ s{T}_l}{s{T}_l} $$
(37)

is applied in the observer-loop. Here T l must be in the range of T, i.e., considerably smaller than T 1 and T 2.

Fig. 9
figure 9

An observer based PID regulator

Full size image

Note that the frequency characteristic of \( \hat{H} \) cannot be easily designed to reach a proper error suppression. For example, it is almost impossible to design a good realizable high cut filter in this architecture. The high frequency domain is always more interesting to speed up a control loop, so the target of the future research is how to select \( {\hat{K}}_l \) for the desired shape of \( \hat{H} \).

6 Simulation Examples

The simulation experiments were performed in using the observer based PID scheme shown in Fig. 9.

Example 1

The process parameters are: T 1 = 20, T 2 = 10 and A = 1. The model parameters are: \( {\hat{T}}_1=25 \), \( {\hat{T}}_2=12 \) and \( \hat{A}=1.2 \). The purpose of the regulation is to speed up the basic step response by 4, i.e., T n  = 5 is selected in the first order R n . In the observer loop a simple proportional regulator \( {\hat{K}}_l=0.01 \) is applied. The ideal form of Q (33) was used. Figure 10 shows some step responses in the operation of the observer based PID regulator.

Fig. 10
figure 10

Step responses using the observer based PID regulator

Full size image

It is easy to see that the \( {\hat{T}}_{\mathrm{ry}}^{\prime } \) very well approximates R n in the high frequencies (for small time values) in spite of the very bad model \( \hat{P} \).

Example 2

The process parameters and the selected first order R n are the same as in the previous example. The model parameters are: \( {\hat{T}}_1=30 \), \( {\hat{T}}_2=20 \) and \( \hat{A}=0.5 \). In the observer loop a PI regulator (37) is applied with A l  = 0.001 and T l  = 2. The ideal form of Q (33) was used. Figure 11 shows some step responses in the operation of the observer based PID regulator.

Fig. 11
figure 11

Step responses using the observer based PID regulator

Full size image

It is easy to see that the \( {\hat{T}}_{\mathrm{ry}}^{\prime } \) well approximates R n in the high frequencies (for small time values) in spite of the very bad model.

7 Conclusions

The TFR of the classical methods are introduced to get a simple and useful tool to analyze and explain further behaviors, which are difficult to obtain using SVR. Using TFR it was shown, if the SVR used in the SFO scheme is model-based then the original (without observer) model error decreases by the sensitivity function of the observer feedback loop. This model error reducing capability gives the theoretical background of the success of practical model-based SFO applications.

Finally the SFO method was applied for the classical IMC structure, opening a new class of methods for open-loop stable processes. This new method combines the classical Youla-parametrization based regulators with the SFO scheme. Using this new approach an observer based PID regulator was also introduced. This regulator works well even in case of large model errors as some simulations showed.