High Temperature and Density in Lattice QCD

Abstract

These lectures provide an introduction to lattice gauge theory calculations of the properties of strongly interacting matter at high temperatures and densities. Such an environment is produced in heavy ion collisions and was most likely present in the early universe. Emphasis is placed, not on formalism, rather on an intuitive understanding of the nature of the crossover from the confined, chiral-symmetry-broken phase to the deconfined, chiral-symmetry-restored phase. Illustrations are taken from results of recent numerical simulations. Connections with phenomenology are discussed.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

$$\displaystyle{\fbox{$\mathbf{Lecture\ 1:\ The\ strong-coupling,\ high-temperature\ limit\ and\ the\ Potts\ model\ paradigm}$}}$$

In this first lecture we survey the phenomenology and offer an intuitive understanding of the phase transitions by appealing to approximate models of lattice QCD applicable at high temperature, strong coupling, and large mass.

6.1 Introduction

6.1.1 Why Study High T and High Density QCD?

Moments after the “big bang”, before the formation of hadrons, the universe passed through a phase in which quarks and gluons (as well as leptons and photons) existed in a plasma-like phase. It is conceivable that, even today, a deconfined state of matter occurs at the cores of very dense stars. This form of strongly interacting matter is not well understood and surely holds interesting surprises. Understanding the properties of matter under such extreme conditions involves both experiment and theory. To study strongly interacting matter under these conditions, we try to recreate it in a microcosm in heavy-ion accelerator laboratories at the Relativistic Heavy Ion Collider at Brookhaven, the Large Hadron Collider at CERN, and at the Facility for Antiproton and Ion Research (FAIR) in Darmstadt, Germany. What we learn provides insights into the origin of matter and the phenomenology of dense stars.

6.1.2 Phenomenology of the Quark-Gluon Plasma

Theoretical studies of the “quark-gluon plasma” have used approximate models, resummed perturbation theory, and nonperturbative numerical simulation to develop some understanding of the properties and behavior of quark-gluon matter at high temperature and density. Some of what we know is well founded in theory and experiment, but much is speculative. Here is a list of the main phenomenologocial properties:

• Deconfinement. At high temperature or density, quarks and gluons are no longer confined in distinct color-singlet combinations.

• Phase transition or crossover. The transition between confined and deconfined matter at zero baryon density is only a crossover and not a true phase transition at physical values of the quark masses.

• Chiral symmetry restoration. The loss of confinement is accompanied by an approximate restoration of chiral symmetry.

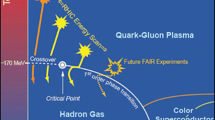
• Phase diagram 1. Figure 6.1 gives a speculative phase diagram as a function of temperature and baryonic chemical potential. The figure indicates a phase boundary between confined matter (hadron gas) and deconfined matter (quark-gluon plasma) as well as some unusual and highly speculative phases at very high density. Sketched are the paths taken as matter evolves in a heavy-ion collision and in the cooling of the early universe.

• Phase diagram 2. Figure 6.2 shows the phase structure as a function of quark mass at zero chemical potential. In this case the regions show for what ranges of quark masses a phase transition of any sort is possible at some temperature. One should imagine a third, temperature axis extending out of the plane. Then what is shown is a projection of phase diagram surfaces onto the quark mass plane. What we see is that at very high quark masses, a first-order phase transition occurs at some temperature. This region is bounded by a second-order line in the Z(2) universality class. At quite low quark masses, there is, again, a first-order phase transition, also bounded by a second order line. This line merges with the m _s axis and extends to infinity. Between these first-order regions there is only a crossover.

Fig. 6.1

Speculative phase diagram for QCD as a function of temperature and baryonic chemical potential. (right) phase structure as a function of the degenerate up/down quark mass and the strange quark mass

Fig. 6.2

Speculative phase structure for QCD as a function of the degenerate up/down quark mass and the strange quark mass

As we have emphasized, these figures mix some solid theoretical results with considerable speculation. So far, there is fairly good agreement about what happens at low baryon number density. There are several open questions: (1) What happens at high density is not well established. (2) At moderately low density, Fig. 6.1 shows a critical point at the end of the first-order line. Is this correct? Is it experimentally accessible? (3) At low up and down quark masses, Fig. 6.2 indicates some uncertainty about whether, at fixed physical strange quark mass, we should encounter a first order phase transition at a nonzero value of the up/down quark mass. Present indications are that, if so, that mass is quite small.

How can we make further progress addressing these questions? They all require a nonperturbative treatment of quantum chromodynamics (QCD). Although the underlying field theory for QCD is well-known and widely accepted, the only reliable method we have for answering nonperturbative questions is through numerical simulation via lattice QCD. This approach is properly called ab initio, since the reliability of its results can be improved indefinitely by decreasing the lattice size (and finding a larger computer!). The lattice version of QCD is not just an approximation. It is a well-defined regularization procedure with a high-momentum cut off that can be removed in the same way as in any standard regularization scheme.

Some disclaimers are in order, however. The numerical methods used to date have their limitations. First, lattice QCD is most naturally designed to describe matter in thermal equilibrium with small perturbations from there. But heavy ion collisions are naturally dynamic. Thus, for example, lattice QCD is not designed for modeling the expansion and cooling of the quark-gluon plasma. Instead, lattice QCD can provide the equilibrium properties of the plasma, which then become inputs to phenomenological models (e.g. hydrodynamic models) of the expansion.

These lectures are intended to give an overview of lattice QCD applied to quark and gluon matter at high temperature and high density. To help develop some intuition about high-temperature lattice QCD, we begin in this lecture by discussing the strong-coupling, high-temperature limit of the theory, making connection with the statistical mechanical three-state, three-dimensional Potts model.

6.2 Lattice QCD at Strong Coupling

We assume familiarity with the basics of lattice gauge theory from chapter “Lattice QCD: A Brief Introduction”.

6.2.1 Partition Function

The imaginary-time Feynman path integral formulation is ideally suited for thermodynamics. With suitable boundary conditions in the imaginary (Euclidean) time dimension, namely, periodic for bosonic fields and antiperiodic for fermionic fields, the integration over classical histories naturally gives us the quantum partition function

$$\displaystyle{ Z =\,\mathrm{ Tr}\exp (-H/T) =\int [\mathit{dU}][d\psi d\bar{\psi }]\exp (-S)\,. }$$

(6.1)

In this notation H is the QCD hamiltonian, T is the temperature, [dU] is the Haar measure over the gauge-field (gluon) links, $[d\psi d\bar{\psi }]$ is the Grassmann measure over the quark and antiquark fields, and S is the classical Euclidean action for QCD.

The temperature is related to the Euclidean time extent of the lattice:

$$\displaystyle{ T = 1/(N_{\tau }a)\,, }$$

(6.2)

where the lattice spacing is a and the number of lattice sites in the Euclidean time direction is N _τ . Thus we can vary the temperature by varying N _τ and by varying a. The latter approach is most widely used.

6.2.2 Wilson Action and Noether Current

The Wilson lattice action S consists of a gauge-field part and a fermion part:

$$\displaystyle{ S = S_{G} + S_{F}\,, }$$

(6.3)

where¹

$$\displaystyle\begin{array}{rcl} S_{G}& =& \frac{6} {g^{2}}\sum _{x,\mu <\nu }[1 -\mbox{ Re}\,\mathrm{Tr}U_{P}(x;\mu,\nu )/3]\,,{}\end{array}$$

(6.4)

$$\displaystyle\begin{array}{rcl} S_{F}& =& \sum _{x}\bar{\psi }(x)\psi (x) \\ & -& \kappa \sum _{x,\mu }[\bar{\psi }(x)(1 +\gamma _{\mu })U_{\mu }(x)\psi (x+\hat{\mu }) +\bar{\psi } (x+\hat{\mu })(1 -\gamma _{\mu })U_{\mu }^{\dag }(x)\psi (x)]\,.{}\end{array}$$

(6.5)

The gauge coupling is denoted by g, the lattice sites, by the four-vector x, the coordinate directions by μ and ν, the plaquette at site x and plane μ, ν, by U _P (x; μ, ν) and the hopping parameter, by κ, which is related to the bare quark mass M through the relationship $\kappa = 1/(2\mathit{aM} + 8)$.

As discussed in chapter “Lattice QCD: A Brief Introduction”, the fermion action is bilinear in the fields, so it can be written in compact form as

$$\displaystyle{ S_{F} =\sum _{x,x^{{\prime}}}\bar{\psi }(x^{{\prime}})M(x^{{\prime}},x)\psi (x)\,. }$$

(6.6)

We saw that the path integral over the fermion fields in Eq. (6.1) could be carried out explicitly, resulting in the determinant of the fermion matrix M(U), leading to an integral over just the gauge field:

$$\displaystyle{ Z_{W} =\int [\mathit{dU}]\exp [-S_{G}(U)]\det [M(U)]\,, }$$

(6.7)

For Monte Carlo integration it is important that the fermionic determinant be real and positive so it can be used as a probability weight for importance sampling. This is true for all fermion formulations commonly used in numerical simulation. The Wilson action in Eq. (6.5) satisfies M ^† = γ ₅ M γ ₅, from which we can infer that detM = detM ^† so the determinant is, indeed, real.

For later reference we write the conserved Noether current for Wilson fermions, which follows in the usual way from the U(1) symmetry of the action:

$$\displaystyle{ J_{\mu }(x) =\kappa [\bar{\psi }(x)(1 +\gamma _{\mu })U_{\mu }(x)\psi (x+\hat{\mu }) -\bar{\psi } (x+\hat{\mu })(1 -\gamma _{\mu })U_{\mu }^{\dag }(x)\psi (x)]\,. }$$

(6.8)

6.2.3 External Point Current

Let us consider introducing an external point charge g in the fundamental representation of SU(3) into the action. Let it move along the world line C. It modifies the continuum action through the source term

$$\displaystyle{ \delta S =\int d^{4}xA_{ a}^{\mu }(x)J_{\mu }^{a}(x) = -\mathit{ig}\oint _{ C}\lambda ^{a}A_{ a}^{\mu }\mathit{dx}_{\mu }\,. }$$

(6.9)

Gauge invariance requires that C be closed. When this term is inserted into the path integral for the partition function we get a path-ordered exponential of the integral over the vector potential.

$$\displaystyle{ P\exp [-\mathit{ig}\oint _{C}\lambda ^{a}A_{ a}^{\mu }\mathit{dx}_{\mu }]\,. }$$

(6.10)

On the lattice this turns into a path-ordered product of gauge links:

$$\displaystyle\begin{array}{rcl} Z& =& \int [\mathit{dU}][d\psi d\psi ]\exp (-S)L_{C}{}\end{array}$$

(6.11)

$$\displaystyle\begin{array}{rcl} L_{C}& =& \,\mathrm{Tr}\prod _{x,\mu \in C}(1 +\gamma _{\mu })U_{x,\mu }\,.{}\end{array}$$

(6.12)

(For backward hopping we use the convention, $\gamma _{-\mu } = -\gamma _{\mu }$ and $U_{-\mu }(x) = U_{\mu }^{\dag }(x-\hat{\mu })$.)

Now we consider placing a static charge in the statistical ensemble. The static charge worldline C is fixed at x, moving forward only in imaginary time τ. The term L _C is then

$$\displaystyle{ L_{C} \propto \,\mathrm{ Tr}\prod _{\tau =0}^{N_{\tau }-1}U_{\mathbf{ x},\tau;0}\,. }$$

(6.13)

It is called a “Polyakov loop” (also, sometimes “Wilson line”).

6.2.4 Gauge Theory at Strong Coupling, High T

Taking soluble limits provides insights into the workings of a theory. We recount an old story that bears repeating for its intuitive value: [402, 403]. We consider the strong-coupling, high-temperature limit of the Wilson action for just the gluons, in other words, pure SU(3) Yang-Mills theory.

The temperature is the inverse of the lattice extent in the imaginary time direction, as in Eq. (6.2). To get a very high temperature we consider an anisotropic lattice, i.e., with different lattice constants in time and space (a _t ≠ a _s ). Then the Wilson action takes the form

$$\displaystyle{ S_{G} = \frac{6a_{s}} {a_{t}g^{2}}\sum _{x,i}[1 -\,\mathrm{ Tr}U_{P}(x;0,i)/3] + \frac{6a_{t}} {a_{s}g^{2}}\sum _{x,i>j}[1 -\,\mathrm{ Tr}U_{P}(x;i,j)/3]\,, }$$

(6.14)

where the space-time oriented plaquettes (first term) get a larger weight than the space-space ones (second term). For high temperature we set N _τ  = 1 so $a_{t} = 1/T$, and we want a _t ∕a _s  ≪ 1. So we may drop the space-space term. We then have only U _P (x, 0) and U _P (x, i) and the space-time-oriented plaquette becomes

$$\displaystyle{ \,\mathrm{Tr}U_{P}(x;0,i) =\,\mathrm{ Tr}U_{0}(\mathbf{x},0)U_{i}(\mathbf{x})U_{0}^{\dag }(\mathbf{x +\hat{ i}})U_{ i}^{\dag }(\mathbf{x})\,. }$$

(6.15)

The trace takes its maximum value of 3 when U ₀(x, 0) = z _x I ∈ Z(3), the center of SU(3): {1, exp(±2π i∕3)}. The center elements commute with the space-like link matrices, which then cancel, leaving only the Z(3) elements. So we approximate the integral over the gauge fields by a sum over elements of Z(3):

$$\displaystyle{ Z =\int \prod _{x,\mu }[\mathit{dU}_{\mu }(x)]\exp (S_{G}) \rightarrow \sum _{z_{\mathbf{x}}}\exp \left [ \frac{6a_{s}} {g^{2}a_{t}}\sum _{\mathbf{x,i}}\mbox{ Re}\left (z_{\mathbf{x}}^{{\ast}}z_{\mathbf{ x}+\hat{i}}\right )\right ]\,. }$$

(6.16)

Our approximation has become the classical three-state, three-dimensional Potts model, a popular toy model in statistical mechanics.

The Potts model is a generalization of the familiar Ising model, but here there are three orientations of each spin, rather than just two. Note that the model has a global Z(3) symmetry: z _x  → Y z _x for Y ∈ Z(3). Just as with the Ising model, the Potts model has a ferromagnetic phase transition from a magnetized (ordered) phase at low temperature where the global symmetry is spontaneously broken to a disordered phase at high temperature. The order parameter is the magnetization, proportional to the expectation value of the spins, $\left \langle z\right \rangle$. In this Potts model the phase transition is first order.

In the spin system, we interpret the factor 6a _s ∕(g ² a _t ) as the ratio J∕T _Potts where J is the coupling strength between neighboring spins, and T _Potts is the spin-lattice temperature. So the Potts temperature T _Potts is proportional to g ² at fixed a _t ∕a _s . Now in QCD the renormalization group tells us that the lattice spacings a _t and a _s must decrease as we decrease g. So at fixed a _t ∕a _s , small g ² corresponds to a high QCD temperature $T_{\mathrm{QCD}} = 1/a_{t}$ and a low Potts model temperature T _Potts.

So from these considerations we expect to find a first order phase transition in SU(3) Yang-Mills theory with an ordered phase at high (QCD) temperature and a disordered phase at low temperature. The order parameter of the transition is TrU ₀(x), the Polyakov loop in this N _τ  = 1 example. For a more extended lattice, it is still the “Polyakov loop”:

$$\displaystyle{ L(\mathbf{x}) = P\exp \left [\int \mathit{ig}A_{0}(\mathbf{x},\tau )d\tau ]\right ]\,. }$$

(6.17)

This quantity should have a zero expectation value in the low-temperature, disordered phase and a nonzero expectation value in the spontaneously broken, ordered high-temperature phase.

6.2.5 Chemical Potential

Before extending the strong-coupling, high-temperature analysis to fermions, we show how to introduce chemical potentials so we can discuss the high temperature approximation at nonzero baryon number density as well.

The conserved charges on the lattice are the flavor numbers (Q _f ) (including baryon number). In the grand canonical ensemble, the partition function is

$$\displaystyle{ Z_{W} =\,\mathrm{ Tr}\exp \left (-H/T +\sum _{f}\mu _{f}Q_{f}/T\right )\,. }$$

(6.18)

The Noether current in Eq. (6.8) gives us the conserved charge density

$$\displaystyle{ \rho _{f}(x) =\kappa [\bar{\psi }_{f}(x)(1 +\gamma _{0})U_{0}(x)\psi _{f}(x +\hat{ 0}) -\bar{\psi }_{f}(x +\hat{ 0})(1 -\gamma _{0})U_{0}^{\dag }(x)\psi _{ f}(x)]\,, }$$

(6.19)

from which we may calculate the contribution to the exponential in the partition function as

$$\displaystyle{ \mu _{f}Q_{f}/T =\mu _{f}\int \sum _{\tau }Q_{f} =\sum _{x}\mu _{f}\rho _{f}(x)\,. }$$

(6.20)

Note that this term is just like the time-like kinetic term in the action except for a sign. We get a factor (1 + a μ) for forward hopping and (1 − a μ) for backward. It is more natural to use e ^{±μ a} for these factors. So we replace

$$\displaystyle\begin{array}{rcl} \bar{\psi }(x)(1 +\gamma _{0})U_{0}(x)\psi (x +\hat{ 0})& \rightarrow & \bar{\psi }(x)(1 +\gamma _{0})U_{0}(x)\psi (x +\hat{ 0})e^{\mu a}\,,{}\end{array}$$

(6.21)

$$\displaystyle\begin{array}{rcl} \bar{\psi }(x +\hat{ 0})(1 -\gamma _{0})U_{0}^{\dag }(x)\psi (x)& \rightarrow & \bar{\psi }(x +\hat{ 0})(1 -\gamma _{ 0})U_{0}^{\dag }(x)\psi (x)e^{-\mu a}\,.{}\end{array}$$

(6.22)

An important consequence of a nonzero chemical potential is that the fermionic determinant detM(μ) is no longer real. We can guess this would happen if we observe that the γ ₅ symmetry we used to prove reality now reads $M^{\dag }(\mu ) =\gamma _{5}M(-\mu )\gamma _{5}$. So $\det [M(\mu )]^{{\ast}} =\det [M(-\mu )]$. It cannot be used directly as a Monte Carlo probability weight. A common expedient is to use the magnitude of the determinant as a probability weight and average over the phase. But the phase oscillations grow with the volume of the system V. So one cannot take the thermodynamic limit V → ∞ with that method.

This vexing problem is called the “sign” problem. It appears in strongly-coupled electron systems as well, when one considers doping to move away from a half-filled conduction band.

6.2.6 Fermions at Strong Coupling, Large Mass, High T

Let’s see what happens to the Potts model approximation when we include fermions. We write the Wilson fermion action for an anisotropic lattice (a _t ≠ a _s ), and we include the chemical potential μ for completeness:

$$\displaystyle\begin{array}{rcl} S_{F}& =& \sum _{x}\bar{\psi }(x)\psi (x) \\ & -& \kappa \sum _{x}[\bar{\psi }(x)(1 +\gamma _{0})U_{0}(x)e^{-\mu a_{t} }\psi (x +\hat{ 0}) \\ & & \qquad \qquad \qquad \qquad +\bar{\psi } (x +\hat{ 0})(1 -\gamma _{0})U_{0}^{\dag }(x)e^{\mu a_{t} }\psi (x)]\, \\ & -& \frac{\kappa a_{t}} {a_{s}}\sum _{x,i}[\bar{\psi }(x)(1 +\gamma _{i})U_{i}(x)\psi (x +\hat{ i}) +\bar{\psi } (x +\hat{ i})(1 -\gamma _{i})U_{i}^{\dag }(x)\psi (x)]\,.{}\end{array}$$

(6.23)

The relationship between bare quark mass and hopping parameter is now

$$\displaystyle{ 1/\kappa = 6a_{t}/a_{s} + 2 + 2\mathit{Ma}_{t}\,. }$$

(6.24)

At very high temperature with N _τ  = 1 we have $a_{t}/a_{s} = 1/(a_{s}T) \rightarrow 0$, so we drop the space-like term in the action. The fermion matrix is then diagonal in space-time with values on each spatial site

$$\displaystyle{ 1 -\kappa (1 +\gamma _{0})ze^{-\mu a_{t} } -\kappa (1 -\gamma _{0})z^{{\ast}}e^{\mu a_{t} }\,, }$$

(6.25)

where we have introduced the Z(3) variable as before.

At large mass (small κ) the fermionic determinant becomes

$$\displaystyle{ \exp \left [h_{0}(\kappa,\mu ) + h(\kappa,\mu )\sum _{\mathbf{x}}\mbox{ Re}z_{\mathbf{x}} + \mathit{ih}^{{\prime}}(\kappa,\mu )\sum _{\mathbf{ x}}\mbox{ Im}z_{\mathbf{x}}\right ]\,, }$$

(6.26)

where

$$\displaystyle{ h(\kappa,\mu ) \approx 24\kappa \cosh (a_{t}\mu )\,,\qquad h^{{\prime}}(\kappa,\mu ) \approx 24\kappa \sinh (a_{ t}\mu )\,. }$$

(6.27)

So our modified Potts model is now

$$\displaystyle{ H = -J\sum _{\mathbf{x,i}}\mbox{ Re}\left (z_{\mathbf{x}}^{{\ast}}z_{\mathbf{ x}+\hat{i}}\right ) -\sum _{\mathbf{x}}[h\,\mbox{ Re}z_{\mathbf{x}} -\mathit{ih}^{{\prime}}\,\mbox{ Im}z_{\mathbf{ x}}] }$$

(6.28)

for values of h, h′ given by Eq. (6.27). So the fermions introduce “external” magnetic fields into the spin system. In the Ising system there is only one magnetic field, but because there are three states in this Potts model, we can have two. In this case the two fields combine to make a complex field. The quark mass introduces an external real magnetic field, and the chemical potential gives rise to an imaginary magnetic field. In the Ising system any nonzero external magnetic field removes the continuous phase transition, resulting in a crossover. At zero field the Potts system has a first order transition, which weakens as the external field is turned on. Eventually, it, too becomes a continuous transition at a critical point and, at higher fields, a crossover. These properties are demonstrated in a numerical simulation of the Potts model [403]. Results are shown in Fig. 6.3. The imaginary field further weakens the transition.

Fig. 6.3

Magnetization vs. inverse Potts temperature in the presence of an external field h. Notice that the first order phase transition disappears with increasing field [403]

The Potts model gives a good understanding of the large-mass portion (upper right corner) of the phase diagram of Fig. 6.2. The first order phase transition degrades into a crossover as the quark masses are decreased. These suggestive features of the approximate model are confirmed in simulations of QCD [404].

6.2.7 Three-Dimensional Flux-Tube Model of QCD

Some years ago, Appoorva Patel introduced an intuitively appealing toy model that imitates strong-coupling, large mass, high-temperature lattice QCD [405, 406], called the “flux-tube model”. The model is equivalent to the three-dimensional three-state Potts model that we have been discussing, but the degrees of freedom are quite different.

The flux-tube model on a cubic lattice places quantized Z(3) electric fluxes ℓ _x, i on next-neighbor links and Z(3) charges n _x on sites. A charge of + 1 on a site represents a quark, − 1, an antiquark, and 0 is an empty site. Fluxes and charges are required to satisfy Gauss’ law mod 3:

$$\displaystyle{ \sum _{i}(\ell_{\mathbf{x},i} -\ell_{\mathbf{x},-i})\mod 3 = n_{\mathbf{x}}\,. }$$

(6.29)

The hamiltonian is, then simply

$$\displaystyle{ H =\sigma \sum _{\mathbf{x,i}}\vert \ell_{\mathbf{x}},i\vert + m\sum _{\mathbf{x}}\vert n_{\mathbf{x}}\vert \,. }$$

(6.30)

where σ is the energy of a flux link and m is the mass of a quark. States of the model must be “singlets” because of the Gauss’ law constraint. As illustrated in Fig. 6.4, there are meson-like states, baryon-like states, and glueball-like states consisting of only a flux loop.

Fig. 6.4

Possible “hadrons” in the flux tube model. Shown are a “meson”, “baryon”, and “glueball”

The grand-canonical ensemble for this classical flux-tube model is defined by the partition function

$$\displaystyle{ Z =\sum _{n_{\mathbf{x}},\ell_{\mathbf{x,i}}}\exp [-(H -\mu N)/T]\,, }$$

(6.31)

where the sum is over configurations that satisfy Gauss’ law and N = ∑ _x n _x . Note that there is no complex phase problem at nonzero chemical potential in this representation.

The equivalence between the flux-tube model and three-dimensional three-state Potts model is easy to show. The essential step in the derivation replaces the Gauss’ Law constraint in the partition function with the Z(3) identity on each lattice site:

$$\displaystyle{ \frac{1} {3}\sum _{z}z^{\ell} =\delta _{\ell,0}\,. }$$

(6.32)

The z’s become the Potts spins. The flux-tube parameters σ, m, and μ map to the Potts model parameters.

There are some amusing features of the deconfined phase of the flux-tube model. At very large quark mass, most of the configurations consist of a continuous fabric of flux links. At low temperature, there are not enough flux links to create a continuous fabric. So one could say at low temperature we have a gas of hadrons, which grow in size as the temperature increases until they connect, leading to the deconfined phase. Quarks terminate flux lines. At lower quark mass there are enough quarks that the fabric is not connected at any temperature, so the phase transition is lost.

We learn from this example that we can solve at least part of the sign problem by a change of basis. In the field basis (gauge links), the complex phase comes from the imbalance between forward time-like and backward time-like hopping, combined with the presence of complex time-like gauge links. Integration over the time-like gauge links enforces Gauss’ Law at each lattice site. Changing from the field basis to the hadron basis eliminates the complex phase.

With SU(3) it is much more difficult to formulate the path integral with a basis change because there are an infinite number of irreducible representations of SU(3). Moreover, there will still be a fermion sign problem, just as with electrons in condensed matter physics. Our simple models don’t expose it. Finally, and probably most importantly, while the Potts and flux-tube models capture the deconfinement aspects of the high temperature phase transition, the strong coupling and large mass approximation doesn’t capture chiral symmetry or its restoration, aspects of the transition that are most important for high temperature physics at physical quark masses.

Exercise 1

In mean field theory we consider the statistical mechanics of a single site, assuming that the neighbors of the site take on the same mean value. So for the Potts model we have a single-site partition function

$$\displaystyle{ Z(\bar{z}) =\sum _{z}\exp [-H(z,\bar{z})/T_{\mathrm{Potts}}]\,, }$$

(6.33)

where the single-site $H(z,\bar{z})$ is obtained from the full H by setting all spins to the mean value $\bar{z}$, except for one site, which carries variable spin z.

We then impose self-consistency by calculating the output mean value of the spin on the single site and requiring that it equal the input mean value.

Do this for the 3D 3-state Potts model with $h = h^{{\prime}} = 0$, and show that there is one real solution for low J∕T and three real nonzero solutions for sufficiently high J∕T. (In the latter case, the middle one happens to be unstable.) Then show that the transition is first order.

Maple, Mathematica, or gnuplot can help with the numerics here.

$$\displaystyle{\fbox{$\mathbf{Lecture\ 2:\ Deconfining\ transition}$}}$$

In this second lecture we consider a variety of deconfinement features of the high temperature transition, including the free energy of a static charge, the strange quark number susceptibility, insights from dimensional reduction, and the survivability of hadrons at high temperature. The equation of state is another, but we defer discussion of that to the last lecture.

6.3 Signals for Deconfinement

6.3.1 Free Energy of a Static Charge

The free energy of a static charge at position x is measured through the expectation value of the Polyakov loop operator, which we introduced in the first lecture:

$$\displaystyle{L(\mathbf{x}) = P\exp \left [\int \mathit{ig}A_{0}(\mathbf{x},\tau )d\tau \right ]}$$

Here $A_{0}(\mathbf{x}) =\sum _{a}\lambda _{a}A_{0}^{a}(\mathbf{x})/2$ is the time component of the color vector potential and P represents path ordering. Its expectation value on the lattice is

$$\displaystyle{ \left \langle L(\mathbf{x})\right \rangle =\int [\mathit{dU}]L(\mathbf{x})\left.\exp [-S_{\mathrm{eff}}(U)]\right /\int [\mathit{dU}]\exp [-S_{\mathrm{eff}}(U)]\,. }$$

(6.34)

As we observed in the first lecture, this operator inserts a static external point source at position x, so its expectation value gives the difference F ₀ in free energy between the ensemble plus an additional static charge and the unmodified ensemble:

$$\displaystyle{ \exp (-F_{0}/T) = \left \langle L\right \rangle \,. }$$

(6.35)

Actually F ₀ = F ₀(a, T) depends on the lattice spacing and temperature. It is ultraviolet divergent ( ∼ const∕a), just as in quantum electrodynamics. Usually, we renormalize it so

$$\displaystyle{ F_{0}(T) \equiv F_{0}(a,T) - F_{0}(a,T_{0}) +\mathrm{ const}\,. }$$

(6.36)

Exercise 2

The Wilson fermion action for a fermion of bare mass m is

$$\displaystyle\begin{array}{rcl} S_{F}& =& \sum _{x,x^{{\prime}}}\bar{\psi }(x)M(x,x^{{\prime}})\psi (x^{{\prime}}) =\sum _{ x}\bar{\psi }(x)\psi (x) \\ & -& \kappa \sum _{x,\mu }[\bar{\psi }(x)(1 +\gamma _{\mu })U_{\mu }(x)\psi (x+\hat{\mu }) +\bar{\psi } (x+\hat{\mu })(1 -\gamma _{\mu })U_{\mu }^{\dag }(x)\psi (x)]\,,{}\end{array}$$

(6.37)

where $\kappa = 1/(8 + 2\mathit{ma})$. The fermion propagator is M ⁻¹(x, x ^′).

Note that $M = 1 -\kappa H$, where H is called the “hopping matrix”. For large bare mass (small κ) the propagator, $[1 -\kappa H]^{-1}$, can be evaluated as a geometric series (hopping parameter expansion). Find the propagator in leading order in κ for a static quark over the time interval [0, t].

The partition function in the presence of a static quark at x is

$$\displaystyle{ \int [\mathit{dU}]\exp [-S_{\mathrm{eff}}(U)]\,\mathrm{Tr}M^{-1}(\mathbf{x},1/T;\mathbf{x},0)\,, }$$

(6.38)

where the trace of the propagator is over color and spin.

So show that $\exp (-F_{0}/T)$ is proportional to the Polyakov loop operator, where F ₀ is the free energy of a static quark, i.e., the difference in the free energies of the ensembles with the static quark and without.

6.3.2 Free Energy of a Pair of Static Charges

Fig. 6.5

Free energy of a static quark/antiquark pair as a function of separation in units of the string tension $R\sqrt{\sigma }$ for a variety of temperatures [407]. Results were calculated with three degenerate flavors of light quarks with masses am _q  = 0. 1 fixed in lattice units. σ is the string tension. The band of lines indicates the Cornell phenomenological heavy quark potential, appropriate at zero temperature. Deviations from this potential with increasing temperature can be interpreted as a weakening of confinement

The free energy of a pair of static charges is constructed in an obvious way from the product of Polyakov loops:

$$\displaystyle{ \exp [-F(\mathbf{R},T,a)/T] = \left \langle L(\mathbf{x})L^{{\ast}}(\mathbf{x + R})\right \rangle \,. }$$

(6.39)

At zero T this is the same as the potential V (R) of separation of a static quark/antiquark pair. Numerical results are shown in Fig. 6.5. If there are no sea quark-antiquark pairs, confinement requires that at large separation

$$\displaystyle{ \lim _{R\rightarrow \infty }F(R) =\sigma R\,. }$$

(6.40)

This form of the free energy is equivalent to the statement that the expectation value of the product of two Polyakov loops at separation R falls exponentially with the area of the region between the loops. Since they are as long as the temporal extent 1∕T of the lattice, the area is R∕T. So $\exp [-F(\mathbf{R},T,a)/T] \rightarrow \exp (-\sigma R/T)$.

When sea quark-antiquark pairs are included in the ensemble, they screen the static charges, as illustrated in Fig. 6.6 (upper left), so we always have, asymptotically, twice the free energy of a single static quark. The result is finite at any temperature:

$$\displaystyle{ F(R,T,a) \rightarrow 2F_{0}(a,T)\,. }$$

(6.41)

When sea quark-antiquark pairs are absent, as in pure Yang-Mills theory, there is no screening, as sketched in Fig. 6.6 (lower right) so F ₀(a, T) is infinite at low temperature. Above the deconfinement temperature the free energy is finite. In pure Yang-Mills theory there is a first-order phase transition separating the deconfined and confined phases. The static quark free energy is an order parameter for the transition.

If we introduce dynamical sea quarks into the ensemble, the static quark free energy is finite at any temperature, but, as long as the quark masses are large, we still see a dramatic decrease in the free energy as we cross the transition temperature. For sufficiently large masses, the transition is still first-order, but as the sea quark masses are decreased, the transition weakens, and eventually there is only a crossover, as shown in Fig. 6.7. In that case the static quark free energy is only a qualitative indicator of deconfinement.

Fig. 6.6

Yellow indicates sea quarks. Brown lines indicate color electric flux. Left, upper: static quarks screened in the presence of sea quarks and lower, unscreened in the absence of sea quarks. Right, upper: static quark at high temperature, screened in the presence of sea quarks and lower, screened by thermal gluon fluctuations in the absence of sea quarks

Fig. 6.7

Free energy of a static quark F _q (T) as a function of temperature in the presence of sea quarks [408]. It drops steadily through the transition temperature between 150 and 200 MeV. There are light sea quarks, so the transition is only a crossover

6.3.3 Strange Quark Number Susceptibility

The number of strange quarks in the ensemble N _s can fluctuate. A measure of fluctuation is the strange quark number susceptibility,

$$\displaystyle{ \chi _{s} = \left \langle N_{s}^{2}\right \rangle /(\mathit{VT})\,. }$$

(6.42)

It is another qualitative indicator of deconfinement, since fluctuations are controlled by the Boltzmann factor. In the low temperature, confined phase, strangeness fluctuations come from fluctuations in the number of strange hadrons. At high temperature they come from fluctuations in the number of strange quarks. Since strange hadrons are heavier than strange quarks, we expect the fluctuations to increase with deconfinement. Results from a numerical simulation are shown in Fig. 6.8.

Fig. 6.8

Strange quark number susceptibility [408], showing a rapid rise in the transition region between 150 and 200 MeV

6.3.4 Dimensional Reduction

Since temperature is determined by the inverse temporal extent of the lattice, high temperature corresponds to a small temporal extent. At sufficiently high temperature, the four-dimensional Euclidean space-time lattice becomes, effectively, a three-dimensional Euclidean lattice. This is called “dimensional reduction.”

Euclidean time boundary conditions

$$\displaystyle\begin{array}{rcl} A_{\mu }^{a}(\mathbf{x},\tau )& =& A_{\mu }^{a}(\mathbf{x},\tau +1/T)\ \ \ \mbox{ periodic}{}\end{array}$$

(6.43)

$$\displaystyle\begin{array}{rcl} q(\mathbf{x},\tau )& =& -q(\mathbf{x},\tau +1/T)\ \ \ \mbox{ antiperiodic}\,,{}\end{array}$$

(6.44)

lead to different behavior for bosons and fermions in the dimensionally reduced lattice. This can be seen from a Fourier decomposition in imaginary time τ:

$$\displaystyle\begin{array}{rcl} A_{\mu }^{a}(\mathbf{x},\tau )& =& \sum _{ n=-\infty }^{\infty }\exp (i\omega _{ b,n}\tau )A_{\mu,n}^{a}(\mathbf{x})\ \ \ \mbox{ for $\omega _{ b,n} = 2\pi n\,T$}{}\end{array}$$

(6.45)

$$\displaystyle\begin{array}{rcl} q(\mathbf{x},0)& =& \sum _{n=-\infty }^{\infty }\exp (i\omega _{ f,n}\tau )q_{n}(\mathbf{x})\ \ \ \mbox{ for $\omega _{f,n} = 2\pi (n + \frac{1} {2} )\,T$}\,.{}\end{array}$$

(6.46)

For free fields the mass-shell condition becomes

$$\displaystyle{ p_{x}^{2} + p_{ y}^{2} + p_{ z}^{2} +\omega _{ n}^{2} + m^{2} = 0\,, }$$

(6.47)

where the fermion Matsubara frequencies are ω _f, n , and the boson Matsubara frequencies are ω _bn .

In a Euclidean world, any direction can be called imaginary time. So we swap z and τ and let E = ip _z . Then the free-field mass-shell condition becomes

$$\displaystyle{ E^{2} = p_{ x}^{2} + p_{ y}^{2} +\omega _{ n}^{2} + m^{2}\,. }$$

(6.48)

We get a tower of 3D bosonic fields, one for each Matsubara frequency:

$$\displaystyle{ E_{n}^{2} = p_{ x}^{2} + p_{ y}^{2} + m_{ b}^{2} + (2\pi \mathit{nT})^{2}\,. }$$

(6.49)

Likewise, we get a tower of 3D fermionic fields, one for each Matsubara frequency:

$$\displaystyle{ E_{n}^{2} = p_{ x}^{2} + p_{ y}^{2} + m_{ f}^{2} + [2\pi (n + \frac{1} {2} )T]^{2}\,. }$$

(6.50)

The result is a three-dimensional Euclidean field theory in which the original time components of the vector potentials A _n, 0 ^a become scalar fields, the original spatial components A _n, i ^a become 3D vector fields and the fermions q _n have effective masses that increase with T. At high T all fermion fields have high mass regardless of m _f , and they are rare. Only the n = 0 bosons are massless when m _b  = 0.

So at high temperature we get a confining zero-temperature 3D Euclidean gauge-Higgs field theory! The 3D coupling is $g\sqrt{T}$. Since it is confining, we get an area law for the Wilson loop, which corresponds to a space-like Wilson loop in 4D. We expect confinement effects for momenta less than g ² T. The confined states in 3D correspond to spatial screening in 4D:

$$\displaystyle{ \left \langle A(0)B(\mathbf{r})\right \rangle \rightarrow \exp (-\mu r)/r\,. }$$

(6.51)

For a quark bilinear, $A =\bar{ q}\varGamma q$, the screening mass at high T is twice the effective mass of the lightest 3D quark (n = 0), or μ ≈ 2π T. Note, also that QCD exhibits “spatial confinement” even at the highest T!

The thermodynamic potential can be calculated in low order QCD perturbation theory. It has the form

$$\displaystyle{ \varOmega (T) = c_{0}(T) +\alpha _{s}c_{1}(T) +\alpha _{ s}^{3/2}c_{ 3/2}(T) +\alpha _{ s}^{2}c_{ 2}(T) +\ldots \,. }$$

(6.52)

Because of spatial confinement, we expect nonperturbative contributions to enter at order α _s ³. A simple way to see that is to note that confinement affects states moving with low momenta, such that p < g ² T. The corresponding volume of phase space goes like g ⁶ T ³.

6.3.5 Hadrons in the Thermal Medium

Another anticipated aspect of deconfinement is that hadrons dissociate. Given that the transition is a crossover, the dissolution should occur gradually as the temperature is increased through the transition. Indeed hadrons might persist as quasi-bound states or resonances at temperatures above the transition. (In a statistical ensemble at any temperature, there are no true bound states because scattering with the medium destroys any initial state.)

The static quark potential in Fig. 6.5 shows short-range attraction even at 1. 15T _c . Of course these results are for static quarks, so they do not account for the response of the medium to the motion of light quarks. Still, they suggest, at least, that heavy quarks might bind, since they move slowly in a bound state, in which case the Born-Oppenheimer approximation might apply.

There is a way, albeit difficult, to study the survival of a hadronic state in a thermal plasma without making the Born-Oppenheimer approximation. This method involves extracting the real-frequency spectral response from the Euclidean time correlator that excites the hadronic state in question. We start with the thermal correlator

$$\displaystyle{ \left \langle \mathcal{O}^{\dag }(\mathbf{x},0)\mathcal{O}(\mathbf{y},\tau )\right \rangle }$$

(6.53)

and do the spatial Fourier transform (using momentum conservation)

$$\displaystyle{ C(p,\tau,T) = \left \langle \mathcal{O}^{\dag }(\mathbf{p},0)\mathcal{O}(\mathbf{p},\tau )\right \rangle \,. }$$

(6.54)

where p =  | p | . The real-frequency spectral decomposition of the correlator reads

$$\displaystyle{ C(p,\tau ) = \frac{1} {2\pi }\int _{0}^{\infty }d\omega \,\rho (\omega,p,T)K(\omega,\tau,T)\,, }$$

(6.55)

where the kernel function is

$$\displaystyle{ K(\omega,\tau,T) = \frac{\cosh \omega (\tau -1/2T)} {\sinh (\omega /2T)} \,. }$$

(6.56)

The spectral density ρ(ω, p, T) has peaks in ω marking resonances that couple to the operators in the correlator. An example for the J∕ψ is shown in Fig. 6.9.

Fig. 6.9

Charmonium spectral density as a function of frequency (energy) at 1. 2T _c (left) and 2. 4T _c (right) from [409], suggesting that charmonium survives at 1. 2T _c , but possibly not at 2. 4T _c

Although the method is interesting, it is numerically extremely challenging. The correlator C(p, τ, T) is measured only for discrete $\tau = 0,1,\ldots,N_{\tau } - 1$. In fact, because of symmetries under τ → N _τ −τ, there are only $N_{\tau }/2 + 1$ independent points (for even N _τ ). But ρ(ω, p, T) has values on the real ω line. Thus solving for the spectral density is an ill-posed problem. To get a meaningful resolution in frequency, one needs a high precision determination of the correlator and many imaginary time points. (An anisotropic lattice with a _t  ≪ a _s helps.) To reduce the ambiguity in the result, it is popular to add extra constraints. A common one goes by the name “maximum entropy” [410]. Essentially, it favors a spectral density that deviates from a default spectral density only as much as required by the data – essentially an Occam’s razor or Bayesian prior. Of course, the result then depends to some extent on the choice of the default spectral density.

The same method is used to extract transport coefficients, such as the electrical conductivity and shear and bulk viscosity, important for hydrodynamics [411, 412]. These quantities control the behavior of the spectral density of the correlator of the electromagnetic current and the stress-energy tensor, respectively, close to zero frequency.

$$\displaystyle{\fbox{$\mathbf{Lecture\ 3:\ Chiral\ symmetry\ restoration}$}}$$

In this third lecture we consider features of the high temperature transition related to the partial restoration of chiral symmetry, including the behavior of the chiral condensate, the chiral susceptibility, and the hadron spectrum. Also discussed is the question of the restoration of the gauge anomaly and an analysis of the universal critical behavior.

6.4 Signals for Chiral Symmetry

Let us recall what is meant by “chiral symmetry”. We start with the continuum Euclidean fermion action for N _f flavors in the presence of a color vector field:

$$\displaystyle{ S_{F} =\sum _{ f=1}^{N_{f} }\int d^{4}x[\bar{\psi }_{ f}(x)\gamma _{\mu }(\partial _{\mu } + \mathit{ig}A_{\mu }^{a}\lambda ^{a}/2)\psi _{ f}(x) + m_{f}\bar{\psi }_{f}(x)\psi _{f}(x)]\,. }$$

(6.57)

If all masses are degenerate, the action is invariant under an SU(N _f ) × U(1) transformation. That is, the action is invariant under an infinitesimal change in the fermion fields ψ(x) → ψ(x) +δ ψ(x), given by

$$\displaystyle{ \delta \psi (x) = \left (i\theta ^{0}/2 + i\theta ^{k}\tau ^{k}/2\right )\psi (x)\,, }$$

(6.58)

where τ ^k are generators of SU(N _f ). A consequence of this symmetry is that hadrons appear in degenerate flavor multiplets.

When the fermion masses are zero the symmetry increases to SU(N _f ) _L ×SU(N _f ) _R × U(1) × U _A (1). The action is invariant under the infinitesimal change

$$\displaystyle\begin{array}{rcl} \delta \psi (x)& =& \left (i\theta ^{0}/2 + i\theta ^{k}\tau ^{k}/2 + i\phi ^{0}\gamma _{ 5}/2 + i\phi ^{k}\tau ^{k}\gamma _{ 5}/2\right )\psi (x)\,,{}\end{array}$$

(6.59)

$$\displaystyle\begin{array}{rcl} \delta \bar{\psi }(x)& =& \bar{\psi }(x)\left (-i\theta ^{0}/2 - i\theta ^{k}\tau ^{k}/2 + i\phi ^{0}\gamma _{ 5}/2 + i\phi ^{k}\tau ^{k}\gamma _{ 5}/2\right )\,.{}\end{array}$$

(6.60)

One might expect larger hadron multiplets as a consequence of this symmetry, but how it is realized in the hadron spectrum depends on mechanisms that break it, as we discuss next.

At zero temperature the U _A (1) symmetry (ϕ ⁰ term) is broken by the gauge anomaly, a quantum effect that appears at one-loop order. Then the axial chiral symmetry (ϕ ^k terms) is broken spontaneously at zero temperature. The breaking of the symmetry results in a nonvanishing expectation value of the “chiral condensates” for each flavor:

$$\displaystyle{ \left \langle \bar{\psi }_{f}\psi _{f}\right \rangle \neq 0\,. }$$

(6.61)

The spontaneous breaking of the ϕ ^k symmetry gives rise to N _f ² − 1 Goldstone bosons. Had the U _A (1) symmetry been spontaneously broken, we would have had one more Goldstone boson.

Since, in nature, the up and down quarks are nearly massless, let us examine in more detail the N _f  = 2 case and consider the transformation of quark bilinears under the chiral symmetry. We define the interpolating operators (f ₀ ≡ σ; a ₀ ≡ δ)

$$\displaystyle\begin{array}{rcl} \pi ^{k} =\bar{\psi }\tau ^{k}\gamma _{ 5}\psi \,,\quad f_{0} =\bar{\psi }\psi \,,& &{}\end{array}$$

(6.62)

$$\displaystyle\begin{array}{rcl} a_{0}^{k} =\bar{\psi }\tau ^{k}\psi \,,\quad \eta =\bar{\psi }\gamma _{ 5}\psi \,.& &{}\end{array}$$

(6.63)

Then under an SU(2) axial transformation

$$\displaystyle\begin{array}{rcl} \delta \pi ^{k} = i\phi ^{k}f_{ 0}\,,\quad \delta f_{0} = i\phi ^{k}\pi ^{k}\,,& &{}\end{array}$$

(6.64)

$$\displaystyle\begin{array}{rcl} \delta a_{0}^{k} = i\phi ^{k}\eta \,,\quad \delta \eta = i\phi ^{k}a_{ 0}^{k}\,,& &{}\end{array}$$

(6.65)

and under a U _A (1) (axial) transformation

$$\displaystyle\begin{array}{rcl} \delta \pi ^{k} = i\phi ^{0}a_{ 0}^{k}\,,\quad \delta f_{ 0} = i\phi ^{0}\eta \,,& &{}\end{array}$$

(6.66)

$$\displaystyle\begin{array}{rcl} \delta a_{0}^{k} = i\phi ^{0}\pi ^{k}\,,\quad \delta \eta = i\phi ^{0}f_{ 0}\,.& &{}\end{array}$$

(6.67)

The mixing of the bilinears under both transformations is mapped in Table 6.1.

Table 6.1 Mixing pattern of quark bilinears for two flavors under SU(2) _L ×SU(2) _R and U _A (1) transformations

6.4.1 Chiral Effective Theory and Symmetry Restoration

When quark masses are not zero, but only small, the Goldstone bosons still have small masses, and they dominate the physics of QCD at low temperature and long wavelength. This observation leads to a low-energy description of QCD, the “chiral effective theory” based on N _f ² − 1 Goldstone bosons, π ^k. The nonlinear version of this theory is usually formulated in terms of the SU(N _f ) fields:

$$\displaystyle{ U =\exp \left (i\hat{\pi }_{k}\tau _{k}/f\right )\,. }$$

(6.68)

Here f is a low energy constant (closely related to the pion decay constant). In terms of these fields the chiral effective Lagrange density is

$$\displaystyle{ \mathcal{L} = \frac{f^{2}} {4} \,\mathrm{Tr}\left (\partial _{\mu }U\partial _{\mu }U^{\dag }\right ) + f^{2}B\,\mbox{ Re}\,\mathrm{Tr}(\mathit{MU})\,, }$$

(6.69)

where M = diag{m ₁, m ₂, …} contains the quark masses. B is another low-energy constant. When M = 0, the Lagrange density is invariant under the chiral transformation

$$\displaystyle{ U \rightarrow V _{R}UV _{L}^{\dag }\,. }$$

(6.70)

If we put the low energy theory on a lattice with spacing a and make the masses degenerate, we can approximate the partial derivatives with

$$\displaystyle{ \partial _{\mu }U(x) \approx [U(x + a\hat{\mu }) - U(x - a\hat{\mu })]/(2a)\,. }$$

(6.71)

If for N _f  = 2 we write $U(x) = u_{0}(x) + i\sum _{k=1}^{3}u_{k}(x)\sigma _{k}$, where u ⋅ u = 1, then the kinetic energy term in the Lagrange density becomes

$$\displaystyle{ \frac{f^{2}} {4a}\left [2 - 2\sum _{\mu }u(x) \cdot u(x + a\hat{\mu })\right ] + 2f^{2}\mathit{Bm}u_{ 0}(x)\,. }$$

(6.72)

This is the Lagrange density for a 3D O(4) ferromagnet. The external field is proportional to the quark mass m, and the magnetization is proportional to $u_{0} =\,\mathrm{ Tr}U/2$. These observations lead to some important consequences for the chiral effective theory and, therefore, for QCD:

• 1. The chiral model behaves like a ferromagnetic spin system. For N _f  = 2 it is equivalent to an O(4) model.

• 2. Quark masses play the role of a magnetic field. Re TrU plays the role of magnetization. It is the analog of $\left \langle \bar{\psi }\psi \right \rangle$.

• 3. At low temperatures we expect spontaneous symmetry breaking, and at high temperatures we expect symmetry restoration, just as with a ferromagnet.

• 4. Restoration of SU(N _f ) _L ×SU(N _f ) _R at high T in QCD, therefore seems certain.

• 5. Restoration of the chiral symmetry is certainly associated with a phase transition. At nonzero quark masses there need not be a phase transition, and the restoration is found to be gradual (a ‘crossover’); at sufficiently high mass we expect no chiral phase transition.

Whether the U _A (1) symmetry is restored is a separate question and depends on the fate of the anomaly at high T. We have not included this symmetry in the simple chiral effective theory above. Pisarski and Wilczek [413] did this and concluded that the nature of the chiral phase transition depends on N _f and on whether the U _A (1) symmetry is simultaneously restored:

• 1. For N _f  ≥ 3 the phase transition is first order.

• 2. The U _A (1) symmetry should be restored at least asymptotically at high T, but its restoration need not occur at the same temperature as that of SU(N _f ) _L ×SU(N _f ) _R .

• 3. For N _f  = 2, the nature of the phase transition depends on what happens with U _A (1).

• 4. If U _A (1) is effectively restored at the same temperature as SU(N _f ) _L ×SU(N _f ) _R , the transition can be a fluctuation-driven first-order transition.

• 5. Otherwise, it is continuous (second order).

Fig. 6.10

A cartoon showing the character of the QCD high temperature phase transition as a function of the light, degenerate (up and down) quark masses and the strange quark mass [414]. Key features are the expected first-order phase transition when all three quark masses are small, the second-order phase transition at zero light quark masses (left axis) when the strange quark mass is large, the first order deconfinement transition when the quark masses are so large, we recover, approximately, the Yang-Mills theory, and the crossover region for intermediate quark masses. Where the physical masses are located in this picture is uncertain, as indicated. In one case, at fixed strange quark mass, there is a first order phase transition at low light quark mass. In the other case there is only a second order transition at zero light quark mass

These observations allow us to characterize the QCD high temperature phase transition as a function of the light quark masses, as shown in Fig. 6.10. The figure is only a sketch. To make it quantitative requires a lattice QCD simulation, which can tell us (1) whether there is a phase transition at the physical (nonzero) values of the light (up and down) quark masses or only at zero quark masses, (2) how large the masses can be before the phase transition is lost, and (3) at what temperature the U _A (1) symmetry is (at least effectively) restored?

6.4.2 Signals of Chiral Symmetry Restoration

We list a variety of indicators of chiral symmetry restoration:

• 1. Chiral condensates $\left \langle \bar{\psi }_{f}\psi _{f}\right \rangle$ The light quark chiral condensate is an order parameter for chiral symmetry. At zero mass it should vanish when the symmetry is restored. If quark masses are not zero, we can still use it as an indicator, even if it is not, strictly, an order parameter.

• 2. Chiral susceptibility $\chi _{f} = \partial \left \langle \bar{\psi }_{f}\psi _{f}\right \rangle /\partial m$ The susceptibility should peak at the transition (or crossover) temperature.

• 3. Hadron correlators Hadron correlators, which imply, also, hadron masses, should become equal. For SU(2) _L ×SU(2) _R we have $C_{\pi }(x) = C_{f_{0}}(x)$.

  $$\displaystyle\begin{array}{rcl} C_{f_{0}}(x)& =& \left \langle f_{0}(x)f_{0}(0)\right \rangle {}\end{array}$$

  (6.73)
  $$\displaystyle\begin{array}{rcl} C_{\pi }(x)\delta _{k,k^{{\prime}}}& =& \left \langle \pi ^{k}(x)\pi ^{k^{{\prime}} }(0)\right \rangle \,. {}\end{array}$$

  (6.74)

  Similarly $C_{\eta }(x) = C_{a_{0}}(x)$. With restoration of U _A (1) we also have $C_{\pi }(x) = C_{a_{0}}(x)$ and $C_{f_{0}}(x) = C_{\eta }(x)$.

We turn, now, to results from lattice simulations that reflect restoration of chiral symmetry. The lattice implementation of chiral symmetry depends on the fermion formulation: The Wilson/clover fermionic actions break chiral symmetry explicitly. The staggered (asqtad, HISQ) fermions preserve a remnant of chiral symmetry. Finally, the overlap and domain wall fermions aim to treat chiral symmetry exactly. For illustration, here, we discuss results for staggered fermions.

The chiral condensate at nonzero quark mass is ultraviolet divergent, which can be seen at one-loop order in QCD perturbation theory:

$$\displaystyle{ \left \langle \bar{\psi }_{f}\psi _{f}\right \rangle = m_{f}/a^{2} +\ldots \,. }$$

(6.75)

Since this divergence appears for each flavor, it can be removed at this order by subtracting the light quark (m _u  = m _d ) and strange quark condensates, leading to the “subtracted condensate”.

$$\displaystyle{ D_{\mathit{ud},s}(T) = [\left \langle \bar{\psi }\psi \right \rangle _{\mathit{ud}} - m_{\mathit{ud}}/m_{s}\left \langle \bar{\psi }\psi \right \rangle _{s}]\,. }$$

(6.76)

The chiral condensate is also subject to a multiplicative renormalization (independent of temperature). This effect can be removed in the ratio

$$\displaystyle{ \varDelta _{\mathit{ud},s}(T) = D_{\mathit{ud},s}(T)/D_{\mathit{ud},s}(T = 0)\,, }$$

(6.77)

before comparing results from different calculations. The resulting quantity from a lattice simulation is shown in Fig. 6.11. We see a rapid decrease in the chiral condensate as temperature is increased through the crossover region. Results for the chiral susceptibility are shown in Fig. 6.12.

Fig. 6.11

Subtracted, normalized chiral condensate as a function of temperature [415]. We see a rapid decrease in the crossover region 150–180 MeV, indicating a partial restoration of chiral symmetry

Fig. 6.12

Unrenormalized chiral (disconnected) susceptibility as a function of temperature [415]. We see a peak in the crossover region 150–180 MeV, an indication of partial restoration of chiral symmetry

As we have remarked above the restoration of the U _A (1) symmetry leads to the equality of the π and a ₀ correlators (of the corresponding local bilinears), C _π (x) and $C_{a_{0}}(x)$. There is a particularly useful connection between the symmetry of the correlators and the spectral density of the Dirac matrix at zero eigenvalue [416]. This is seen by considering the related susceptibilities,

$$\displaystyle{ \chi _{S} = \left \langle \int C_{a_{0}}(x)d^{4}x\right \rangle \,,\quad \chi _{ P} = \left \langle \int C_{\pi }(x)d^{4}x\right \rangle \,, }$$

(6.78)

which must also be equal. The susceptibilities are particularly useful, because they are related to the eigenspectrum of the lattice Dirac matrix:

$$\displaystyle\begin{array}{rcl} \left \langle \bar{\psi }\psi \right \rangle & =& -m\int _{-\infty }^{\infty }d\lambda \frac{\rho (\lambda )} {\lambda ^{2} + m^{2}}{}\end{array}$$

(6.79)

$$\displaystyle\begin{array}{rcl} \chi _{P} -\chi _{S}& =& \int _{-\infty }^{\infty }d\lambda \frac{2m^{2}\rho (\lambda )} {(\lambda ^{2} + m^{2})^{2}}{}\end{array}$$

(6.80)

where m is the degenerate up and down quark mass and ρ(λ) is the eigenvalue density. These expressions can be derived from a spectral decomposition of the quark propagators involved in the correlators. As the quark masses are decreased to zero, we get

$$\displaystyle{ \lim _{m\rightarrow 0}\left \langle \bar{\psi }\psi \right \rangle = -\pi \rho (0)\,, }$$

(6.81)

also known as the Banks-Casher relation [31]. Restoration of the SU(2) _L ×SU(2) _R symmetry implies that $\left \langle \bar{\psi }\psi \right \rangle = 0$, so then ρ(0) = 0. If a gap opens in the spectrum at λ = 0, then certainly $\chi _{P} -\chi _{S} = 0$ in the limit of zero mass. If, instead, the spectral density vanishes as ρ(λ) = A λ ^α, with suitable α, we can have vanishing $\left \langle \bar{\psi }\psi \right \rangle$ and nonvanishing χ _P −χ _S .

Thus a study of the eigenvalue density at small eigenvalue can help in testing the restoration of the U _A (1) symmetry. An example of a numerical test of these ideas is given in Figs. 6.13 and 6.14 [416]. Lattice results thus far suggest that the U _A (1) symmetry is not restored at the same temperature as SU(2) _L ×SU(2) _R , but more work is needed [417]. For a recent domain wall study on smaller lattices, see [418].

Fig. 6.13

Eigenvalue density as a function of eigenvalue for various temperatures [416]. There appears to be a zero for T > 168 MeV indicating restoration of the SU(2) _L ×SU(2) _R chiral symmetry

Exercise 3

In terms of the Euclidean Dirac matrix $M = m + D\!\!\!\!/\,$, the chiral condensate is

$$\displaystyle{ \left \langle \bar{\psi }\psi \right \rangle =\,\mathrm{ Tr}M^{-1}\,. }$$

(6.82)

The eigenvalues and eigenvectors of D​​​​∕ satisfy M u _n  = i λ _n u _n . Assume that the antihermitian D​​​​∕ operator also satisfies the anticommutation relation $\{D\!\!\!\!/\,,\gamma _{5}\} = 0$.

Prove that (Banks-Casher)

$$\displaystyle{ \left \langle \bar{\psi }\psi \right \rangle = -m\int _{-\infty }^{\infty }d\lambda \frac{\rho (\lambda )} {\lambda ^{2} + m^{2}}\,. }$$

(6.83)

where the spectral density is constructed from $1/V \sum _{n} \rightarrow \int d\lambda \rho (\lambda )$.

Then show that at zero mass $\left \langle \bar{\psi }\psi \right \rangle = -\pi \rho (0)$.

Fig. 6.14

Eigenvalue density as a function of eigenvalue for various temperatures [416]. Whether the apparent gap for T > 240 MeV is significant remains to be studied further [417]

6.4.3 Universality and Critical Behavior

The theory of critical phenomena places systems in universality classes according to their symmetries and spatial dimension. They alone determine the critical exponents and universal scaling functions that control scaling and the functional dependence of key quantities close to the critical point.

For the remainder of this lecture we will assume that the critical point appears only at T = T _c ⁰ and m _ud  = 0. Since the relevant chiral symmetry is SU(2) _L ×SU(2) _R , equivalent to O(4), QCD is expected to fall into the 3D O(4) universality class. Staggered fermion implementations preserve a reduced symmetry, suggesting an O(2) behavior at nonzero lattice spacing. The critical behavior of these two universality classes is very similar.

We discuss the critical behavior in QCD by rescaling T and m _ud to give t and h:

$$\displaystyle\begin{array}{rcl} t& =& \frac{1} {t_{0}} \frac{T - T_{c}^{0}} {T_{c}^{0}} \,,{}\end{array}$$

(6.84)

$$\displaystyle\begin{array}{rcl} h& =& \frac{1} {h_{0}}H\ \ \mbox{ for $H = m_{\mathit{ud}}/m_{s}$}\,,{}\end{array}$$

(6.85)

where m _ud ∕m _s is the ratio of light to strange quark masses. The quantities t ₀ and h ₀ are constants. These variables correspond to the temperature and magnetic field in the O(4) spin system.

The free energy density as a function of quark masses and temperature in the vicinity of a critical point has two contributions, a universal singular part and a regular part.

$$\displaystyle{ f = -\frac{T} {V }\log Z \equiv f_{\mathrm{sing}}(t,h) + f_{\mathrm{reg}}(T,m_{\mathit{ud}},m_{s})\;\,. }$$

(6.86)

Up to a rescaling of the variables (via h ₀ and t ₀), the singular part is universal. It can be expressed in terms of a universal function of a single scaling variable $z = t/h^{1/\beta \delta }$ where δ and β are universal critical exponents. The singular part is then

$$\displaystyle{ f_{\mathrm{sing}}(t,h) = h^{1/\delta }f_{ s}(z)\,, }$$

(6.87)

where f _s (z) is universal. (In the condensed matter literature, it is often called the “equation of state”.) So, for example, the scaling function f _s (z) in the 3D O(4) model is the same as the QCD scaling function.

The free energy is thermodynamically fundamental, since most physical observables can be expressed as derivatives of the free energy. For many observables the singular part dominates over the regular part close to the critical point. Where this happens is called the Landau region. The size of this region is not universal.

The chiral condensate plays the role of magnetization in QCD. We define

$$\displaystyle{ M_{b} \equiv \frac{m_{s}\left \langle \bar{\psi }\psi \right \rangle _{\mathit{ud}}} {T^{4}} \,, }$$

(6.88)

where

$$\displaystyle{ \left \langle \bar{\psi }\psi \right \rangle _{\mathit{ud}} = T/V \partial \log Z/\partial m_{\mathit{ud}}\,. }$$

(6.89)

Then

$$\displaystyle{ M_{b}(T,H) = h^{1/\delta }f_{ G}(t/h^{1/\beta \delta }) + f_{ M,\mathrm{reg}}(T,H)\,, }$$

(6.90)

where the function f _G is universal. The chiral susceptibility is the derivative

$$\displaystyle{ \chi _{\mathit{ud}} = \frac{\partial } {\partial m_{\mathit{ud}}}\left \langle \bar{\psi }\psi \right \rangle _{\mathit{ud}}\,. }$$

(6.91)

We get a scaling expression for it by differentiation

$$\displaystyle{ \frac{\chi _{\mathit{ud}}} {T^{2}} = \frac{T^{2}} {m_{s}^{2}}\left ( \frac{1} {h_{0}}h^{1/\delta -1}f_{\chi }(z) + \frac{\partial f_{M,reg}(T,H)} {\partial H} \right )\,, }$$

(6.92)

where

$$\displaystyle{ f_{\chi }(z) = \frac{1} {\delta } \left [f_{G}(z) -\frac{z} {\beta } f_{G}'(z)\right ]\,. }$$

(6.93)

So the behavior of $\left \langle \bar{\psi }\psi \right \rangle _{\mathit{ud}}$ and χ _ud is governed by the same singular function.

A fit to lattice measurements using this analysis is shown in Fig. 6.15. The universal scaling function used in the fit was taken from a separate study of the O(4) spin model. To obtain the agreement shown, it was necessary to include a regular part, parameterized with its leading-order Taylor expansion in the scaling variables. A byproduct of this analysis was the value T _c  = 154(9) MeV for the crossover temperature at physical quark masses

Fig. 6.15

Fit to the chiral condensate (left) and susceptibility (right) to the same scaling function plus a small regular part [415]

$$\displaystyle{\fbox{$\mathbf{Lecture\ 4:\ Connection\ with\ phenomenology}$}}$$

In this fourth and last lecture we consider a variety of observables of more direct interest to the phenomonology of heavy ion collisions, including the equation of state at zero and nonzero density, the charm quark contribution to the equation of state, and fluctuations in conserved charges.

6.5 Equation of State

6.5.1 Models at Low and High Temperature

At extremes of temperatures some approximations are possible. We discuss the hadron resonance gas model, applicable at low temperature and the Stefan-Boltzmann gas model, at high temperature.

6.5.1.1 Hadron Resonance Gas Model

The hadron resonance gas model is a simple (simple-minded!) model often used as an approximation to the low temperature behavior of QCD. Introduced by Hagedorn, it approximates the QCD ensemble as a noninteracting gas of mesons and baryons, including resonances. All particles (and resonances) listed in the Particl Data Group summary are included. One stops at some cut off mass M. Interactions are treated only in the sense that resonances are included. One expects the model to be good for T ≪ m _π , the lowest mass. If the density of states grows as $\mathit{dN}/\mathit{dm} = C\exp (m/T_{c})$ then the partition function diverges for T > T _c (Hagedorn limiting temperature). At this point one has to change the model by switching to quark and gluon degrees of freedom for T > T _c .

In the low temperature limit we get an explicit expression for the partition function for mesons/baryons (M/B):

$$\displaystyle{ \log \mathcal{Z} =\sum _{i}\log \mathcal{Z}^{\mathcal{M}} +\sum _{ i}\log \mathcal{Z}^{\mathcal{B}}\,. }$$

(6.94)

For the ith meson or baryon we have

$$\displaystyle\begin{array}{rcl} \log \mathcal{Z}_{M_{i}}^{M/B}& =& \mp \frac{\mathit{Vd}_{i}} {2\pi ^{2}} \int _{0}^{\infty }\mathit{dk}k^{2}\log (1 \mp z_{ i}e^{-\varepsilon _{i}/T})\; \\ & =& \frac{\mathit{VT}^{3}} {2\pi ^{2}} d_{i}\left (\frac{M_{i}} {T} \right )^{2}\sum _{ k=1}^{\infty }(\pm 1)^{k+1}\frac{z_{i}^{k}} {k^{2}} K_{2}(\mathit{kM}_{i}/T)\,,{}\end{array}$$

(6.95)

where d _i is a multiplicity factor.

6.5.1.2 Stefan-Boltzmann Limit

In the high temperature limit the QCD running coupling is expected to be small, so we can treat the quarks and gluons as approximately noninteracting and massless, leading to the relativistic ideal gas limit (Stefan-Boltzmann gas). In the presence of a chemical potential μ _f for conserved flavor number N _f , the Stefan-Boltzmann pressure is

$$\displaystyle\begin{array}{rcl} \frac{p_{\mathit{SB}}} {T^{4}} = \frac{8\pi ^{2}} {45} + \frac{7\pi ^{2}} {20} +\sum _{f=u,d,s}\left [\frac{1} {2}\left ( \frac{\mu _{f}} {T}\right )^{2} + \frac{1} {4\pi ^{2}}\left ( \frac{\mu _{f}} {T}\right )^{4}\right ]\,.& &{}\end{array}$$

(6.96)

6.5.2 Equation of State at Zero Density

More generally, at any temperature thermodynamic identities relate the energy density and pressure to the partition function as follows:

$$\displaystyle\begin{array}{rcl} \varepsilon & =& \frac{T^{2}} {V } \left.\frac{\partial \log Z} {\partial T}\right \vert _{V }{}\end{array}$$

(6.97)

$$\displaystyle\begin{array}{rcl} p& =& T\left. \frac{\partial } {\partial V }\log Z\right \vert _{T}\,.{}\end{array}$$

(6.98)

To calculate them separately on the lattice is a bit involved. It is more convenient to calculate the “interaction measure”

$$\displaystyle{ I =\varepsilon -3p = -\frac{T} {V } \frac{d\log Z} {d\log a} \,. }$$

(6.99)

For the Wilson gauge action we get

$$\displaystyle{ I = -T/V (d\log g^{2}/d\log a)\left \langle S_{ G}\right \rangle \,. }$$

(6.100)

We must subtract the vacuum value to remove an ultraviolet divergence. From now on, we assume this has been done and drop the Δ.

$$\displaystyle{ \varDelta I = I(T) - I(0)\,. }$$

(6.101)

Exercise 4

The previous discussion gives the thermodynamic identities that relate the energy density and pressure to derivatives of the ensemble free energy with respect to temperature and volume, respectively. On a lattice of a fixed number of sites N _s ³ × N _t , the volume is given in terms of the spatial and temporal lattice constants a _s and a _t by N _s ³ a _s ³, and the inverse temperature is given by a _t N _t . So we can relate the derivatives in the thermodynamic identities to derivatives with respect to a _s and a _t . To relate these derivatives to the lattice action, one must take care to include the appropriate factors of a _s and a _t in the expression for the lattice action and to remember that the gauge coupling g ² also depends on the lattice constants.

With these preliminaries in mind, show that

$$\displaystyle{ I \equiv \varepsilon -3p = -T/V (d\log g^{2}/d\log a)\left \langle S_{ G}\right \rangle \,. }$$

(6.102)

For sufficiently large volume the pressure is independent of volume:

$$\displaystyle{ \log Z = \mathit{pV }/T\,. }$$

(6.103)

so the interaction measure is

$$\displaystyle{ I = -\frac{T} {V } \frac{d(\mathit{pV }/T)} {d\log a} \,, }$$

(6.104)

and, if the temperature is varied by varying a with fixed N _τ , we can determine the pressure from it by integrating from low temperature (large a = a ₀) to high temperature (small a).

$$\displaystyle{ p(a)a^{4} - p(a_{ 0})a_{0}^{4} = -\int _{\log a_{0}}^{\log a}\varDelta I(a^{{\prime}})(a^{{\prime}})^{4}\,d\log a^{{\prime}}\,. }$$

(6.105)

At sufficiently low T ₀ we may take p(a ₀) = 0, or take its small value from the hadron resonance gas model.

Exercise 5

Derive the integral expression for the pressure in Eq. (6.105).

For illustration we show some lattice results for a variety of thermodynamic quantities obtained in the past few years. To find the most recent results, the proceedings of the annual Lattice conferences are a good place to start.²

Fig. 6.16

Interaction measure $\varepsilon -3p$ as a function of temperature [408]. As the lattice spacing is decreased the peak softens a bit

Fig. 6.17

Energy density and three times pressure as a function of temperature from [408]. We see a strong increase in the temperature range 150–200 MeV. These results are for higher than physical mass and for nonzero lattice spacing

Fig. 6.18

Entropy density as a function of temperature from [408]

Fig. 6.19

Speed of sound from [408]

Results for the interaction measure are shown in Fig. 6.16. The corresponding energy density and pressure are shown in Fig. 6.17. Next, the entropy density $s = (\varepsilon +p)/T$ is shown in Fig. 6.18. Finally, the speed of sound is

$$\displaystyle{ c_{s}^{2} = \frac{\mathrm{d}p} {\mathrm{d}\epsilon } =\epsilon \frac{\mathrm{d}(p/\epsilon )} {\mathrm{d}\epsilon } + \frac{p} {\epsilon } \,. }$$

(6.106)

It is illustrated in Fig. 6.19. All of these quantities are of importance for hydrodynamic modeling of the quark-gluon plasma. However, it should be noted that these results are for higher than physical mass and for nonzero lattice spacing and require extrapolation to physical values to be realistic.

6.5.3 Equation of State at Nonzero Density

We observed in the first lecture that we cannot simulate directly at μ ≠ 0, because the fermion determinant is complex. For heavy ion collisions, the chemical potentials are small. Therefore, one is led to a Taylor series expansion for small μ. For the 2 + 1 flavor case, the expansion reads

$$\displaystyle{ \frac{p} {T^{4}} =\sum _{ n,m=0}^{\infty }c_{\mathit{ nm}}(T)\left (\frac{\mu _{\mathit{ud}}} {T} \right )^{n}\left ( \frac{\mu _{s}} {T}\right )^{m}\,, }$$

(6.107)

The coefficients are evaluated at $\mu _{\mathit{ud}} =\mu _{s} = 0$

$$\displaystyle{ c_{\mathit{nm}}(T) = \left. \frac{1} {n!} \frac{1} {m!} \frac{1} {T^{3}V } \frac{\partial ^{n+m}\log Z} {\partial (\mu _{\mathit{ud}}/T)^{n}\partial (\mu _{s}/T)^{m}}\right \vert _{\mu _{\mathit{ud},s}=0}\,. }$$

(6.108)

The derivatives are expectation values of combinations of traces of the inverse of the lattice Dirac matrix. An example of a calculation at nonzero chemical potential is given in Fig. 6.20. As in this figure, the results are often shown at fixed ratios of entropy density to baryon density. Since in heavy ion collisions the strange number density n _s is zero, it is necessary to tune $\mu _{\ell} =\mu _{u} =\mu _{d}$ and μ _s to get n _s  = 0 at fixed s∕n _B . The tuned trajectories are shown in Fig. 6.21. One often assumes an isentropic formation and expansion of the plasma. The equation of state at constant entropy along the trajectories plotted in Fig. 6.21 is shown in Fig. 6.20.

Fig. 6.20

Isentropic equation of state: energy density as a function of temperature at three constant ratios s∕n _B of entropy density to baryon number density from [419]

Fig. 6.21

Tuned values of the light quark chemical potential μ _ℓ and strange quark chemical potential μ _h as a function of temperature giving zero strangeness density at three fixed ratios s∕n _B of entropy density to baryon number density [420]

6.5.4 Charm Quark Contribution

It is interesting to consider how charm quarks contribute to the equation of state. Whether the quark plasma in a heavy ion collision has time to equilibrate charm is an open question, but in the early universe it certainly does. The charm contribution to the equation of state can be done without including charm quarks explicitly in the statistical ensemble (quenched charm) with the result shown in Fig. 6.22. We see that charm effects start to become visible above about T = 200 MeV. The stout and p4 action results are a bit smaller than the result from the asqtad action.

Fig. 6.22

Contribution of the charm quark to the equation of state [419]

6.6 Fluctuations of Conserved Charges

In a neutral ensemble, conserved charges still fluctuate about zero.

$$\displaystyle{ \delta N_{X} \equiv N_{X} -\overline{N_{X}}\,. }$$

(6.109)

So we define susceptibilities of the generic form,

$$\displaystyle{ \chi _{2}^{X} =\langle (\delta N_{ X})^{2}\rangle /(\mathit{VT}^{3})\,, }$$

(6.110)

for X = baryon number B, strangeness S, and electric charge Q. They can be derived from the second-order Taylor coefficients in the expansion of the pressure in terms of the chemical potentials:

$$\displaystyle\begin{array}{rcl} \chi _{2}^{X}& =& \left.\frac{\partial ^{2}p/T^{4}} {\partial \hat{\mu }_{X}^{2}} \right \vert _{\boldsymbol{\mu }=0}\,,{}\end{array}$$

(6.111)

$$\displaystyle\begin{array}{rcl} \chi _{11}^{\mathit{XY}}& =& \left.\frac{\partial ^{2}p/T^{4}} {\partial \hat{\mu }_{X}\partial \hat{\mu }_{Y }} \right \vert _{\boldsymbol{\mu }=0}\,,{}\end{array}$$

(6.112)

where $\hat{\mu }_{X} = \mu _{X}/T$. Results for these quantities are shown in Fig. 6.23.

Fig. 6.23

Fluctuations in baryon number B, electric charge Q, and strangeness S as a function of temperature from [421]. Plotted is the lattice susceptibility divided by the hadron-resonance-gas susceptibility. The magenta bars and cyan bands show results of two extrapolations to zero lattice spacing. We see that the HRG agrees reasonably well for B and Q, but not S

Conclusions

What has lattice QCD taught us about the behavior of QCD at high temperature and density?

• 1. We have learned a great deal about the qualitative behavior of QCD in thermal equilibrium at low chemical potential for a few flavors and nonzero quark masses. This reach of lattice QCD is illustrated in Fig. 6.24.

• 2. We have fairly good control of a variety of important quantities needed for hydrodynamic modeling.

• 3. We have good quantitative predictions for fluctuations in conserved charges.

What might lattice QCD still teach us?

• 1. We need better ideas/methods for dealing with higher baryon density.

• 2. We hope to learn more about whether the critical endpoint is accessible to experiment.

• 3. We expect to learn more about transport properties: viscosity, electric conductivity, etc. This is difficult, though.

• 4. We do not yet have a completely satisfactory understanding of what happens at the chiral critical point at low m _u  = m _d , but this will come.

• 5. We expect to learn more about the behavior of the QGP in strong magnetic fields.

Fig. 6.24

A speculative phase diagram for high temperature and density QCD. The shaded region indicates the current reach of lattice QCD