Two Simple Constructive algorithms for the Distributed Assembly Permutation Flowshop Scheduling Problem

Abstract

Nowadays, it is necessary to improve the management of complex supply chains which are often composed of multi-plant facilities. This paper proposes a Distributed Assembly Permutation Flowshop Scheduling Problem (DAPFSP). This problem is a generalization of the Distributed Permutation Flowshop Scheduling Problem (DPFSP) presented by Naderi and Ruiz (Comput Oper Res, 37(4):754–768, 2010). The first stage of the DAPFSP is composed of f identical production factories. Each center is a flowshop that produces jobs that have to be assembled into final products in a second assembly stage. The objective is to minimize the makespan. Two simple constructive algorithms are proposed to solve the problem. Two complete sets of instances (small-large) are considered to evaluate performance of the proposed algorithms.

1 Introduction

Assembly systems have been widely studied in the last decade given their practical interest and applications. An assembly flowshop is a hybrid production system where various production operations are independently and concurrently performed to make parts that are delivered to an assembly line [4]. Tozkapan et al. [8] considered a two-stage assembly scheduling problem by minimizing the total weighted flow time as an objective function. Al-Anzi and Allahverdi [1] addressed the model presented by [8] and minimized the total completion time of all the jobs by using metaheuristics to solve their model. This is just a small extract of the many existing papers in this regard.

From a manager’s point of view, scheduling in these systems is more complicated than in single-factory settings. In single-factory problems, the only objective is to find a job schedule for a set of machines, while an important additional decision in the distributed problem is allocating jobs to suitable factories.

In this paper, flowshop scheduling is used as a production system for each factory or supplier in the distributed problem. The flowshop scheduling problem (FSP) is composed of a set of M of m machines where each job of a set N of n jobs must be processed in each machine. The number of operations per job is equal to the number of machines. The i ^th operation of each job is processed in machine i. Therefore, one job can start in machine i only after it has been completed in machine i−1, and if machine i is free. The processing times of each job in the machines are known in advance, non-negative and deterministic. In FSPs, a number of assumptions are made [2].

In the FSP, there are n! possible job permutations for each machine. Therefore, the total number of solutions for a flowshop problem with m machines is (n!)^m. To simplify the problem, it is assumed that all machines have the same job permutation. With this simplifying assumption the FSP is referred to as Permutation Flowshop Scheduling Problem (PFSP) with n! possible solutions. This problem is one of the most researched topics in the scheduling literature [6, 7, etc.]. The DPFSP can be viewed as a generalized version of the PFSP.

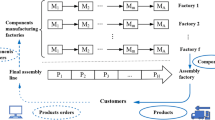
This paper studies the Distributed Assembly Permutation Flowshop Scheduling Problem (DAPFSP). It is a combination of the DPFSP and the Assembly Flowshop Scheduling Problem (AFSP), and consists of two stages: production and assembly. The first stage comprises of a set F of f factories or production centers where a set N of n jobs has to be scheduled. All factories are capable of processing all jobs and each factory is a PFSP with a set M of m machines. Factories are assumed to be identical. Processing times are denoted by ${p_{ij}},,j \in N$. The second stage is a single assembly factory with an assembly machine, M _A , which assembles jobs by using a defined assembly program to make a set T of t different final products. Each product has a defined assembly program. N _h and J _i are used, respectively, to represent product’s h assembly program and the jobs that belong to the product’s h assembly program, ${N_h}:\left\{ {{J_j}} \right\},\,J \in {N_h}$. Each product h has N _h jobs and job j is needed for the assembly of one product. Therefore, $\sum\limits_{h = 1}^t {\left| {{N_h}} \right| = n}$. Product h assembly can start only when all jobs that belong to N _h have been completed in the different factories. The considered objective is to minimize the makespan at the last assembly factory.

Despite the innumerable literature related to PFSP and AFSP, it seems that there are few studies about the DPFSP. Naderi and Ruiz [5] presented the DPFSP for the first time and developed six different MILPs , proposed two simple factory ­assignment rules and 14 heuristics based on dispatching rules, effective constructive heuristics and VND methods. To the best of our knowledge, no further literature exists on DAPFSP, so this is the first effort that considers the assembly flowshop problem in a distributed manufacturing setting.

The next section presents introduces two simple constructive algorithms, Sect. 3 describes a complete computational evaluation of the proposed algorithms. Finally, Sect. 4 offers conclusions, remarks and venues for future research.

2 Heuristic Methods

As mentioned in the paper of [5], the DPFSP is an NP-Complete problem (if n>f); accordingly, the DAPFSP with an additional assembly stage is certainly an NP-Complete problem (or rather, one should say that the associated decision problem is). Therefore, it is necessary to develop a heuristic approach to solve large-sized problems.

For the assignment of jobs to factories, the two rules (NR ₁, NR ₂), of [5] are used. Using these two factory allocation rules, two heuristics are presented to schedule jobs.

2.1 Heuristic 1

We first introduce some necessary notation. An example with n = 9, m = 2, f = 2 and t = 3, this is, 9 jobs, 2 factories with a flowshop of two machines each and three products to assemble, is employed to explain expressions and heuristics in some detail. The processing times of the 9 jobs on the first and second machines on factories are {1, 5, 7, 9, 9, 3, 8, 4, 2} and {3, 8, 5, 7, 3, 4, 1, 3, 5}, respectively. Assembly processing times of products on assembly machine are 6, 19 and 12 respectively. The products’ assembly programs are: N₁ = {3,4,6}, N₂ = {1,2,8,9} and N₃ = {5,7}. π represents a product sequence, e.g., π = {1,3,2} is a possible product sequence for the given example. As mentioned before, each product h is made up of |N_h| jobs and π_h is the partial job sequence of product h, e.g., π₁:{6,4,3}, π₂:{1,9,8,2}, π₃:{7,5}. A complete job sequence, π_T, is constructed by putting together all partial job sequences, following the product sequence π, e.g., π_T:{6,4,3,7,5,1,9,8,2}.

The shortest processing time (SPT) is a well-known dispatching rule for the PFSP. Hence the SPT is used to determine the product sequence in the assembly machine.

Heuristic 1 begins by applying the SPT rule for the assembly operation times to obtain π, π = {1,3,2}. A heuristic which is based on [3] heuristic (FL) is applied on the jobs that belong to a given product.

The heuristic evaluates the completion times of the jobs that belong to product h, for example if, h = 1. Set R_h is made by sorting jobs in ascending order of ­completion times, R ₁ = {6,3,4}. Where completion times for set of jobs of the product 1, N ₁ = {3,4,6} are C ₂₃ = 12, C ₂₄ = 16, C ₂₆ = 7. The first two jobs of R_h are selected and inserted into S_h, S ₁ = {6,3}. All jobs’ pairwise exchanges in S_h are checked and it is updated with the one that results in the best makespan, C _max({6,3}) = 15 and C _max({3,6}) = 16, S ₁:{6,3}. The next step is removing the third job of R_hand inserting it in all possible positions of S_h , C _max({4,6,3}) = 25, C _max({6,4,3}) = 24 and C _max({6,4,3}) = 26. The sequence with the best makespan will be selected, S ₁ is updated to {6,4,3}. All possible sequences by carrying out pairwise exchanges between jobs are evaluated again, C _max({4,6,3}) = 25, C _max({6,4,3}) = 24, C _max({3,4,6}) = 27. If a better makespan is obtained, then S_h is updated. The process continues until all jobs have been considered. S_h is the partial job sequence for product h, (π_h), π₁ = {6,4,3}. By following the same method, the partial job sequences for the other products are: π₂ = {1,9,8,2} and π₃ = {5,7} with partial makespans of 20 and 18, respectively. π_T is constructed by putting together all π_h and jobs are assigned to factories from π_T by using NR₁ or NR₂, which respectively result in the H₁₁ or H₁₂ heuristics. Hence π_T is {6,4,3,5,7,1,9,8,2}. The final step is to assign jobs in π_T to factories by using NR ₁/NR ₂ to obtain the H ₁₁/H ₁₂. C _max of H ₁₁ and H ₁₂ are 55 and 53, respectively. The Gantt chart of the considered example after applying H ₁₁ is shown in Fig. 1.

2.2 Heuristic 2

The idea of the second heuristic is to give priority to products whose jobs are completed in the production stage sooner. This concept is noted as the earliest start time to assemble product h, E _h . The procedure that is used in H ₁₁ and H ₁₂ to find partial job sequences of products (π_h) also is used in heuristic 2. E _h , is calculated by using NR ₁ or NR ₂ to assign jobs in each partial job sequence to factories. For example, the earliest start times for assembling products by considering NR ₂ are E ₁ = 15, E ₂ = 15, E ₃ = 12. π is built by sorting E _h in ascending order.

Fig. 1

Gantt chart of H ₁₁ for the example

3 Computational Evaluation

Two complete sets of instances have been generated to test the proposed heuristics. Four instance factors (n.m, f,t) are combined at the levels provided for small and large instances. In small instances, number of jobs (n) is tested at 5 levels, 8, 12, 16, 20 and 24, number of machines (m) has 4 levels, 2, 3, 4 and 5, both factors of number of factories (f) and number of products (t) have 3 levels, 2, 3 and 4. In the large instances, all factors have 3 levels and are; n = {100, 200, 500}, m = {5, 10 20}, f = {4, 6, 8} and t = {30, 40, 50}.

Processing times in the production stage are fixed to $\cup \;[1,99]$as it is usual in the scheduling literature. The assembly processing times depend on the number of jobs assigned to each product h as $U\left[ {1 \times \left| {{N_h}} \right|,99 \times \left| {{N_h}} \right|} \right]$. The total number of combinations in the small and large instances are $5 \times 4 \times {3^2} = 180$ and ${3^4} = 81$, respectively. There are five replications per combination for small instances and ten replications for every large combination. Therefore, the total number of instances is 900 and 810, respectively. All instances are available at soa.iti.es.

3.1 Heuristics Evaluation on Small Instances

The four proposed methods (H ₁₁,H ₁₂,H ₂₁,H ₂₂) are tested. A MILP model is constructed for the small instances are solved with two commercial solver packages (CPLEX 12.3 and GUROBI 4.6.1). Serial (1 thread) and parallel (2 threads) and two time limits (900 and 3600 s) are tested with the solvers.

As the proposed heuristics are not expected to find an optimal solution, the Relative Percentage Deviation (RPD), is measured for comparisons. We measure RPD as follows: using the optimal solution or the best known solution, (OPT _best ) and ALG _SOL , which reports the makespan obtained by a given algorithm for a given instance:

$$RPD = \frac{{AL{G_{SOL}} - OP{T_{best}}}}{{OP{T_{best}}}} \times 100$$

Table 1 provides the summarized results of the MILP and the average algorithm deviations from the best known solution for the small instances. They are grouped by n and f

Table 1 Relative Percentage Deviation (RPD) of MILP and proposed algorithms over the best known solution for the small instances

MILP reports better results when compared to the proposed heuristics. CPU times to solve small instances with the proposed algorithms are negligible while most of the instances that are solved with the MILP. Therefore, the 3 % average deviation of ${H_{22}}$ needs to be contextualized.

In order to identify the best algorithm, a means plot and Tukey’s Honest Significant Difference (HSD) intervals (99 % confidence) for the four simple constructive heuristics is shown in Fig. 2. The second heuristic performs better in comparison with the other simple constructive heuristic and there is no significant difference between the rules used to assign jobs to factories.

3.2 Heuristics Evaluation on Large Instances

In this case, for calculating the RPD, only the best known solution is used as the MILP cannot be employed. A summarized result of the average RPD, considering number of factories, number of products and number of jobs, is shown in Table 2. Figure 2 shows a means plot (99 % confidence level Tukey’s HSD intervals) of the proposed algorithms for large instances.

Table 2 Relative Percentage Deviation (RPD) for the proposed algorithms over the best known solution for the large instances

The second proposed algorithm performs better than the first one also for the large instances. NR ₂ as a job assignment rule, reports better results on the first algorithm while job assignment rule on second algorithms does not have any significant effect. It is clear on Table 2, generally when the number of factories and jobs increases, finding a better solution becomes easier, while this trend has a reverse effect when the number of products increases. Proposed simple constructive algorithms use a very short time in order to solve problems (less than 0.01 s on average), therefore the details are not reported.

Fig. 2

Means plot and 99 % confidence level Tukey’s HSD intervals of the relative percentage deviation for simple constructive heuristic methods for small instances on the left and for large instances on the right

4 Conclusion and Future Research

To the best of our knowledge, this paper is the first attempt to generalize the Distributed Permutation Flowshop Scheduling Problem to the Distributed Assembly Permutation Flowshop Scheduling Problem, where there is more than one production center to process jobs and a single assembly center to make final products from produced jobs. Two constructive algorithms are proposed.

Computational evaluations were performed with two groups of small and large instances. Results show that in small instances MILP reported results perform better than the proposed algorithms. On the other side, the proposed methods consume very little CPU time in comparison with the MILP while they still produce reasonable solutions.

For future works, the setup time and distinct production factories can be considered in the presented model to make it more realistic. Applying metaheuristics like a Genetic Algorithm, Tabu Search, etc., may report better solutions if compared to our proposed simple heuristics.