Keywords

The solution of the wave propagation problem in plate-like composites in the case of excitation by piezoelectric actuators modelled using a pin-force model is obtained as a sum of propagating Lamb wave modes. It is calculated in the frequency-wavenumber domain and then transformed into the time–space domain. The harmonic wave responses of composite plates and corresponding energy flows are analyzed for various excitation sources at the surface of some composites.

1 Introduction

In recent years composites become to be widely used in civil, mechanical, and aerospace engineering due to their high strength and lightness in comparison with metals. Due to the sensitivity of composites to impact actions small damages in the form of cracks or delaminations are practically unavoidable. These small damages could potentially result in the destruction of the construction. In the field of structural health monitoring (SHM) [1] there has been a growing interest in the recent decade in developing computer-aided systems for the detection of mechanical defects and the forecasting of destruction [2] in composite structures. It is hoped that SHM systems will be able to regularly scan high-duty structural components (e.g. wind power rotor blades, aircraft panels and wings) and issue warnings concerning the formation of defects as well as provide an estimate of the remaining useful life. The use of SHM systems can increase safety and can allow for a change of the maintenance procedure for aircraft from schedule-driven to condition-based, can reduce the fuel costs and the costs of maintenance significantly, and decrease the time required for the structure to be off-line [3].

One of the promising approaches for SHM consists of applying guided elastic waves since the waves excited or reflected by damages provide significant information on the nature and properties of the defect. An improved inspection potential of guided waves over other ultrasonic methods is due to their sensitivity to different type of flaws, their propagation over long distances and their capability to follow curvature and to reach hidden and/or buried parts. The level of understanding which has been reached in an application of elastic waves for NDT (non-destructive testing) and SHM is documented in review works [2] and [4], respectively. A clear understanding of quantitative connections between the waves and their sources is essential for the development of algorithms to detect defects. Moreover, information about the structure in its undamaged state is required since by relating the measured response with one in the same but undamaged structure allows the considerable improvements in the precision of quantitative damage detection. This is shown in case of the application of an approach based on damage influence maps in [5].

Due to the finite dimensions of structural components the waves reflect from the structural boundaries, i.e. the waves guide through the structure. Such structures in many cases can be considered as infinite layers (beams) or plates. The first numerical results which relate to the characteristics of normal waves in a layer can be found in Lamb’s work [6]. He was the first to obtain a dispersion equation linking frequencies and wave numbers. Hence, the waves in layer-like and plate-like structures are usually called (guided) Lamb waves. Theoretical principles of wave propagation in isotropic, anisotropic and layered materials, as well as principles of wave excitation with standard ultrasonic transducers for nondestructive evaluation, are described in many works, e.g. in [7, 8]. The application of elastic waves for NDT was first studied by Viktorov [9]. However, in these works the waveguides are modelled in two dimensions (plane strain problem), i.e. it is assumed that waves are excited by sources whose distribution is infinitely expanded in the direction perpendicular to the cross-section. To accurately model finite source induced wave propagation in anisotropic composite plates, a 3D formulation is required [10]. Dispersion relations for waves in multilayered media with an arbitrary number of flat layers were derived for a plain strain (2D) problem using a transfer [11] and a global [12] matrix method and then extended by Nayfeh [13] to the case of 3D-models of composites in which the layers can have as low as monoclinic symmetry. Up to date, there are many methods for the computation of dispersion properties of laminated composites [14]. Analysis of dispersion properties of Lamb waves in anisotropic composites shows that in addition to the frequency dispersion the angular dispersion of waves should be taken into account. Moreover, some directions are privileged for the transport of energy of the guided waves, i.e. the waves are focussed [15].

Taking into account the dispersion properties of waves the problem of wave propagation excited by surface sources can be studied. For in situ monitoring of structures low-cost surface-coupled [1] or embedded piezoelectric actuators [5] are used. Due to the piezoelectric effect the wafers can be used not only as actuators but also as sensors. The corresponding forced wave propagation problem can be resolved by applying direct numerical methods: conventional FEM [16], spectral FEM [5], strip element method (SEM) [14] and finite difference technique (FD) [17]. A good review of all these direct numerical approaches is given in [18]. The application of direct numerical methods for the modelling of constructions made of composites is the most universal approach, as these yield approximate solution for objects of any form. However, they are also the most expensive with regard to computational resources and do not take into account the wave structure of the solution. An increase in the number of elements is unavoidable in regions of rapid changes of the solutions or characteristics of the medium (angular points, interfaces between contrast layers etc.) and especially in the case of high frequencies. In some papers the FEM is used only for that part of a construction which has a complex form and comparable sizes in all directions, whereas for the part of the construction which is a typical waveguide the solution is constructed as a sum of propagating waves using the mode expansion technique (NME) [19].

The most time-efficient approach for the simulation of piezo-excited wave propagation is the semi-analytical integral approach. The corresponding solutions of wave propagation problem are obtained for 2D-models for isotropic and anisotropic laminates [20] and 3D-models for isotropic laminates under excitation by axis-symmetric sources [21]. The solution of the general 3D-problem for anisotropic laminates is obtained for the far-field area of the excitation source [22] and well approximated for the middle field to the source [23] by applying the integral approach.

In this work the integral approach is used for time-efficient simulations of steady-state piezo-excited Lamb wave propagation in composites and for the investigation of the anisotropy-induced properties of guided waves by computing the peak-to-peak amplitude curves and the power flow corresponding to each Lamb wave mode.

2 Mathematical Background

2.1 Modeling of the Wave Propagation Problem

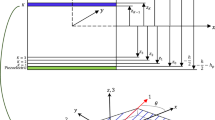
In the absence of body forces the harmonic steady-state motions in each layer of composite plate (Fig. 13.1) after omitting the factor exp(iωt) are expressed in terms of stress and displacement components:

Fig. 13.1
figure 1

N-layered plate under an excitation by a ring-shaped source (inner radius A i , outer radius A o )

Full size image
$$ \frac{{\partial \sigma_{ij} }}{{\partial x_{j} }} = - \rho \omega^{2} u_{i} . $$
(13.1)

The stresses in (13.1) are found using Hooke’s law:

$$ \sigma_{ij} = C_{ijkl} \varepsilon_{kl} ,\quad \quad \varepsilon_{ij} = \frac{1}{2}\left( {u_{i,j} + u_{j,i} } \right), $$
(13.2)

where C ijkl are the components of the stiffness tensor.

The waves are excited in a laminated plate by the force q(x, y) applied in the domain Ω at the upper surface of the plate, whereas the lower boundary is traction-free:

$$ \left. {\sigma_{i3} } \right|_{z = 0} = q\left( {x,y} \right),\;\quad \left. {\sigma_{i3} } \right|_{z = - h} = 0. $$
(13.3)

As surface excitation sources, a circular piezoelectric actuator (Fig. 13.2a), a CLoVER sector (Fig. 13.2b) and MFC actuator (Fig. 13.2c) are considered. A nearly ideal bonding of the actuators to the composite plate is assumed, i.e. the thickness of the glue layer is supposed to satisfy h b → 0 (see Fig. 13.3). The force is transferred over an infinitesimal region at the edges of the patch. The induced strain is assumed to be given by concentrated forces applied at the region ends. This model is also called the pin-force model [24] and was originally derived for isotropic structures under excitation by piezoelectric patches. However, this model proved itself applicable also in 3D-models of piezo-structure interaction and is therefore used in this work.

Fig. 13.2
figure 2

a Circular piezoactuator, b CLoVER sector, c MFC actuator

Full size image
Fig. 13.3
figure 3

2D-Model of piezoactuator bonded by a layer of glue to the plate

Full size image

Then, the corresponding surface load vectors for the first two piezoactuators considered (Fig. 13.2a and b) are given as follows

$$ q_{x} = \tau_{0} \cdot q_{r} \cdot \cos \varphi ,\quad q_{y} = \tau_{0} \cdot q_{r} \cdot \sin \varphi ,\quad q_{z} = 0, $$
(13.4)

where for a circular actuator (Fig. 13.2a) q r is represented by

$$ q_{r} = \delta \left( {r - A_{o} } \right),\quad \forall \left( {r,\varphi } \right), $$
(13.5)

and for a CLoVER sector (Fig. 13.2b) by

$$ q_{r} = \delta \left( {r - A_{o} } \right) - \delta \left( {r - A_{i} } \right),\quad \forall r,\varphi \in \left[ {\varphi_{R} ,\varphi_{L} } \right], $$
(13.6)

respectively.

For MFC actuator (Fig. 13.2c) the load vector is given by

$$ q_{x} = \tau_{0} \left[ {\delta \left( {x - a_{1} } \right) - \delta \left( {x + a_{1} } \right)} \right],\quad q_{y} = 0,\quad q_{z} = 0,\quad y \in \left[ { - a_{2} ,a_{2} } \right] $$
(13.7)

The value of τ 0 is obtained as [24]

$$ \tau_{0} = {{G_{b} \varepsilon_{ISA} } \mathord{\left/ {\vphantom {{G_{b} \varepsilon_{ISA} } {h_{b} \Gamma^{2} a^{2} }}} \right. \kern-0pt} {h_{b} \Gamma^{2} a^{2} }}, $$
(13.8)

here

$$ \Gamma^{2} = \frac{{G_{b} }}{{E_{a} }}\frac{1}{{h_{a} h_{b} }}\frac{\alpha + \psi }{\psi },\quad \quad \psi = \frac{Eh}{{E_{A} h_{a} }},\quad \quad \varepsilon_{ISA} = d_{31} \frac{V\left( t \right)}{{h_{a} }}, $$
(13.9)

where d 31 is the piezoelectric strain coefficient (in m/V) describing the coupling between the vertically polarized electric field and the in-plane induced strains, h a is the thickness of the piezoactuator, E a is its Young’s modulus, G b is the shear modulus of the bonding (adhesive) layer, h b is the thickness of the adhesive layer, h is the thickness of the structure under excitation, E is the Young’s modulus of the structure. Outside of the interval |x| < a, the surface stresses are zero. The modal repartition number α in (13.8) depends on the stress, strain, and displacement distributions across the plate thickness [24] and at low frequencies α = 1 for wave mode S 0, α = 3 for wave mode A 0 and α = 4 in case of simultaneous excitation of both modes. For the accurate calculation of this parameter at high frequencies the readers are referred to the work [3].

2.2 Solution of the Wave Propagation Problem

The problem (13.1–13.3) can be relatively easy solved in the wavenumber-frequency domain [26]. In cylindrical coordinates the displacement vector of the corresponding steady-state problem can be found as the inverse Fourier transform of the product of the Green’s matrix k(r, φ, z, ω) and the load vector q(r, φ) in wavenumber-frequency domain K(α, γ, z, ω) and Q(α, γ), respectively:

$$ u\left( {r,\varphi ,z,\omega } \right) = \frac{1}{{4\pi^{2} }}\int\limits_{0}^{2\pi } {\int\limits_{{\Gamma_{ + } }}^{{}} {K\left( {\alpha ,\gamma ,z,\omega } \right)} } Q\left( {\alpha ,\gamma } \right)e^{{ - i\alpha r\cos \left( {\gamma - \varphi } \right)}} \alpha d\alpha d\gamma . $$
(13.10)

where the contour Γ+ is chosen so that it encloses all the real poles of the integrand in accordance with the principle of limiting absorption. There are two possible time-efficient approaches for the evaluation of the double integral (13.10): the far-field residue integration technique (FFRIT) and the asymptotic expansion (AE). The FFRIT gives an approximate solution in the middle field and an exact solution in the far-field of the excitation source for all types of sources in the following form [23]:

$$ u\left( {r,\varphi ,z,\omega } \right) = \sum\limits_{m = 1}^{\infty } {\left[ {u_{m}^{ + } + u_{m}^{ - } } \right] - d\left( {r,\varphi ,z,\omega } \right)} , $$
(13.11)
$$ u_{m}^{ \pm } \left( {r,\varphi ,z,\omega } \right) = \pm \frac{i}{2\pi }\int\limits_{{\varphi \pm {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}}^{{\varphi + \pi \pm {\pi \mathord{\left/ {\vphantom {\pi 2}} \right. \kern-0pt} 2}}} {b_{m}^{ \pm } \left( {\gamma ,z,\omega } \right)e^{{ - ik_{m}^{ \pm } \left( \gamma \right)r\cos \left( {\gamma - \varphi } \right)}} d\gamma } , $$
(13.12)
$$ d\left( {r,\varphi ,z,\omega } \right) = \frac{1}{2\pi r}\sum\limits_{m = 1}^{\infty } {\left[ {\left. {\frac{{b_{m}^{ \pm } \left( {\gamma ,z,\omega } \right)}}{{k_{m}^{ \pm } \left( \gamma \right)}}} \right|_{{\gamma = \varphi + \frac{3\pi }{2}}} + \left. {\frac{{b_{m}^{ \pm } \left( {\gamma ,z,\omega } \right)}}{{k_{m}^{ \pm } \left( \gamma \right)}}} \right|_{{\gamma = \varphi + \frac{\pi }{2}}} } \right]} + O\left( {r^{ - 2} } \right), $$
(13.13)
$$ b_{m}^{ \pm } \left( {\gamma ,z,\omega } \right) = \left. {{\text{res}}\;K\left( {\alpha ,\gamma ,z,\omega } \right)} \right|_{{\alpha = k_{m}^{ \pm } \left( \gamma \right)}} Q\left( {k_{m}^{ \pm } \left( \gamma \right),\gamma } \right)k_{m}^{ \pm } \left( \gamma \right), $$
(13.14)

where k ± m (γ) are the dependencies of the wave numbers on the angle γ for the fixed frequency ω.

The asymptotic expansion (AE) represents the solution of the wave propagation problem for the far-field points to the excitation source as follows [22]

$$ u\left( {r,\varphi ,z,\omega } \right) = \sum\limits_{m = 1}^{{N_{r} }} {\sum\limits_{p = 1}^{{N_{mp}^{ + } \left( \varphi \right)}} {G_{mp} \left( {r,\varphi ,z,\omega } \right)} } + O\left( {r^{{ - {\raise0.7ex\hbox{$3$} \!\mathord{\left/ {\vphantom {3 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}}} } \right), $$
(13.15)
$$ G_{mp} \left( {r,\varphi ,z,\omega } \right) = \pm \frac{i}{2\pi }\sqrt {\frac{2\pi }{r}} \frac{{b_{m}^{ \pm } \left( {\gamma_{mp}^{ \pm } \left( \varphi \right),z,\omega } \right)}}{{\sqrt { - i \cdot P_{m,\gamma \gamma }^{\prime \prime \pm } \left( {\gamma_{mp}^{ \pm } \left( \varphi \right),\varphi } \right)} }}e^{{irP_{m,\gamma \gamma }^{ \pm } \left( {\gamma_{mp}^{ \pm } \left( \varphi \right),\varphi } \right)}} , $$
(13.16)
$$ P_{m}^{ \pm } \left( {\gamma ,\varphi } \right) = - k_{m}^{ \pm } \left( \gamma \right)\cos \left( {\gamma - \varphi } \right),\quad P_{m,\gamma \gamma }^{\prime \prime \pm } \left( {\gamma_{m}^{ \pm } \left( \varphi \right),\varphi } \right) \ne 0, $$
(13.17)

where γ ± mp (φ) are the stationary points of the phase function (13.16) for the wavenumber curve k ± m (γ).

2.3 Energy Fluxes Corresponding to Lamb Waves

The energy brought into the structure by a surface source and its radiation through the structure to infinity is studied using the definitions of values of power flow and the vector of its power density usually called Poynting (or frequently called Umov-Poynting) vector. The energy brought into a composite plate by the surface source q(x *, y) acting in the domain Ω is obtained as

$$ E_{0}^{\omega } = - \frac{\omega }{2}\text{Im} \int\limits_{0}^{2\pi } {\int\limits_{{\Gamma_{ + } }}^{{}} {\left( {K\left( {\alpha ,\gamma ,z,\omega } \right)Q\left( {\alpha ,\gamma } \right),Q\left( {{\alpha}^{*},\gamma } \right)} \right)} } \alpha d\alpha d\gamma . $$
(13.18)

The density of energy flux through the surface S in the direction of its normal n at a point x ∊ S is given by the scalar product of the displacement vector and the complex stress vector calculated in direction of normal n

$$ E\left( {R,\varphi ,z,\omega } \right) = \left( {u\left( {R,\varphi ,z,\omega } \right),\sigma_{n} \left( {R,\varphi ,z,\omega } \right)} \right)\,{\text{with}}\,\sigma_{n,i} \left( {R,\varphi ,z,\omega } \right) = \sum\limits_{j = 1}^{3} {\sigma_{ij} \cdot n_{j} } . $$
(13.19)

The energy propagating from the source to infinity can be evaluated in the same way. A cylinder is taken outside of the source, which is located inside the circle with a minimum radius A o , i.e. the radius of the cylinder satisfies R > A o while its center is located at the origin. The height of the cylinder is equal to the thickness of the laminated plate h. The total through-thickness power flow for r = R is given by

$$ E_{R,\varphi }^{\omega } \left( {R,\varphi ,\omega } \right) = - \frac{\omega R}{2}\text{Im} \int\limits_{ - h}^{0} {E\left( {R,\varphi ,z,\omega } \right)} dz. $$
(13.20)

While computing the energy flow for different values of R, φ and z using both approaches (13.11–13.13) and (13.15–13.17) the total power density of the energy propagating from the source to infinity can be obtained as

$$ \begin{aligned} E\left( {R,\varphi ,z,\omega } \right) = & \left( {\sum\limits_{j} {u_{j} \left( {R,\varphi ,z,\omega } \right)} ,\sum\limits_{k} {\sigma_{n,k} \left( {R,\varphi ,z,\omega } \right)} } \right) = \sum\limits_{j} {\left( {u_{j} \left( {R,\varphi ,z,\omega } \right),\sigma_{n,j} \left( {R,\varphi ,z,\omega } \right)} \right)} \\ & + \sum\limits_{j,k,j \ne k} {\left[ {\left( {u_{j} \left( {R,\varphi ,z,\omega } \right),\sigma_{n,k} \left( {R,\varphi ,z,\omega } \right)} \right) + \left( {u_{k} \left( {R,\varphi ,z,\omega } \right),\sigma_{n,j} \left( {R,\varphi ,z,\omega } \right)} \right)} \right]} , \\ \end{aligned} $$
(13.21)

i.e. as the sum of contributions to the power density corresponding to wave modes solely and some mixed values of power density.

3 Numerical Results and Discussion

In this section some results of numerical computations of piezo-excited Lamb wave propagation and the corresponding power flows in composite plates are presented. As waveguides three composite specimens are considered. The first one is a cross-ply composite with stacking sequence [0/90]s and all plies manufactured of fiber-reinforced polymer (CFRP-T700GC/M21), whose elastic moduli and density are given in Table 13.1. The second plate is a hybrid plate with stacking sequence [I90/C45/C-45]s, where “I” stands for layers made of IM7-Cycom-977-3 (see Table 13.1) and “C” stands for layers manufactured of CFRP-T700GC/M21. The third plate is a quasi-isotropic plate [0/45/-45/90]2s with layers manufactured of CFRP-T700GC/M21. All values of stiffness for both materials CFRP-T700GC/M21 and IM7-Cycom-977-3 given in Table 13.1 correspond to the well-known Voigt notation for the stiffness tensor C ijkl (13.2). All of the composite plates considered have a total thickness of 1 mm.

Table 13.1 Properties of materials (elastic constants in 1011 Pa, density in 103 kg/m3)
Full size table

In the following example (Fig. 13.4a) the total through-thickness power density of the energy flow is analyzed in dependence of the direction φ. Here the power flow (13.20) is calculated for r = 100 mm and r = 220 mm evaluated using FFRIT for [0/90]s made of CFRP-T700GC/M21 under excitation by the circular source (A o = 10 mm) for f = 300 kHz. In Fig. 13.4a some differences between the distributions of power flow are observed in directions, in which the power flow has its maxima. This is explained by the fact that the distribution in the near-field of the source is mostly formed by the shape of the actuator and the near-field terms, whereas in the far-field the distribution of power flow is mostly conditioned by the anisotropy-induced energy focusing in directions φ = 0°, φ = 7°, etc. [23]. Note that the asymptotic expansion (AE) by its definition gives a distribution of power flow with respect to propagation direction independently of the distance to the excitation source. This means that for a good quantitative description of the wave phenomena in the middle-field for strong focusing of waves the FFRIT has to be used. However, for qualitative analysis the AE is usually enough even for the middle-field area.

Fig. 13.4
figure 4

a The total through-thickness power flow in dependence on φ for r = 100 mm and r = 220 mm calculated using FFRIT for [0/90]s made of CFRP-T700GC/M21 under excitation by the circular source (A o = 10 mm) for 300 kHz. b Out-of-plane amplitudes in dependence on φ and f = ω/2π calculated using FFRIT in a cross-ply [0/90]s plate under an excitation by the circular source (A o = 5 mm) at r = 46 mm for the sum of S 0 and SH 0 wave modes

Full size image

The focusing of waves in Fig. 13.4a in directions φ = 0°, φ = 7° is due to the focusing of the wave modes S 0 and SH 0 in these directions. However, the behavior of the corresponding distribution is frequency-dependent, e.g. for lower frequencies it is mostly influenced by the A 0 wave mode. Moreover, as can be observed in Fig. 13.4b, the distribution of amplitudes and hence of the power flow for S 0 and SH 0 wave modes is also frequency-dependent. For frequencies above 150 kHz these wave modes are strongly focused in directions φ = 0° and φ = 90°, while at lower frequencies this effect is negligible.

Another phenomenon occurring in composite plates under excitation by some types of piezoelectric actuators is the presence of frequency- and direction-dependent anti-resonances. They occur due to the anti-phase action of the boundaries of the piezoactuator, where the interface stresses are concentrated. Since the wavenumbers are frequency- and direction-dependent, resonances and anti-resonances occur for the different directions not simultaneously. This phenomenon is well observed in Fig. 13.5a for the logarithmical surface out-of-plane displacements corresponding to the A 0 wave mode, excited in a cross-ply [0/90]s made of CFRP-T700GC/M21 by a circular actuator of radius A o = 5 mm. Comparing the corresponding logarithmical displacements in the directions of φ = 0°, φ = 45° and φ = 90° (Fig. 13.5b), it is clearly seen that the difference between the anti-resonance frequencies is about 45 kHz. This implies that if the waves are excited for one direction at the anti-resonance, in some other directions no anti-resonance occurs at the given frequency. Moreover, in the case of strong anisotropy of wavenumbers of wave modes in such directions the amplitudes of observed waves can be high. It is concluded that for excitation at frequency higher than the first anti-resonance frequency it is nearly impossible to suppress (or to amplify) the wave propagation of the wave mode in all directions of the composite simultaneously. Note that such a suppression (or amplification) can be easily carried out for isotropic structures [1].

Fig. 13.5
figure 5

a Surface out-of-plane logarithmic displacements (lg|u z (φ, ω)|) at r = 46 mm for the wave mode A 0 calculated using AE for the case of wave excitation by a circular actuator (A o = 5 mm) in a [0/90]s plate with layers made of CFRP-T700GC/M21, b The same displacements in some fixed directions

Full size image

The anti-resonances observed in Fig. 13.5 for the A 0 wave mode for the whole considered frequency range [0, 500] KHz are not observed in this frequency range for the two other fundamental wave modes S 0 and SH 0. The total through-thickness power flow corresponding to the S 0 wave mode is represented in Fig. 13.6a for an excitation by the CLoVER sector (A i = 4 mm, A o = 5 mm, φ R = 22.5°, φ L = 67.5°). The power flow is despite of the use of the CLoVER sector is focussed in the whole range of frequencies below the 500 kHz in the directions φ = 4° and φ = 86°. Comparing Fig. 13.6a with the similar Fig. 13.4b for the circular piezoactuator lets us conclude that the use of a CLoVER sector slightly shifts the maxima of amplitudes (and energy too). For a circular piezoactuator they are φ = 0° and φ = 90°.

Fig. 13.6
figure 6

Total through-thickness power flow for r = 150 mm calculated using AE in dependence on φ and f, calculated for the S 0 wave mode in a cross-ply [0/90]s plate a Under an excitation by a CLoVER sector (A i = 4 mm, A o = 5 mm, φ R = 22.5o, φ L = 67.5°) and a hybrid [I90/C45/C–45] s plate b Under an excitation by a circular source (A o = 5 mm)

Full size image

Another interesting numerical example is shown in Fig. 13.6b. The distribution of the total through-thickness power flow for the S 0 wave mode in a hybrid [I90/C45/C − 45] s plate under an excitation by a circular source (A o = 5 mm) has focusing directions too, but they vary with the frequency. For example, for a frequency of 200 kHz the focusing direction is φ = 50°, whereas for 500 kHz the main focusing direction in the first quarter changes to φ = 60° and, moreover, the power flow in the direction of φ = 50° for a frequency of 500 kHz is quite low. Similarly to the case of a cross-ply plate the focusing of the S 0 wave mode is not observed for low frequencies (below 100 kHz).

The effects of energy focusing observed in composite plates with strong influence of anisotropy are also present in quasi-isotropic composites, however for high frequencies or for the case of the non-axis-symmetric source. In Fig. 13.7a and b the total through-thickness power flows are shown for S 0 (Fig. 13.7a) and for SH 0 (Fig. 13.7b) excited in a quasi-isotropic [0/45/–45/90]2s plate under an excitation by an MFC source (A 1 = 8 mm, A 2 = 2 mm). Here an MFC actuator produces for the S 0 wave mode a power flow mostly in fiber direction in MFC (φ = 0°), i.e. the highest values of amplitudes (power flow) are usually between the directions φ = [−atan(2/8), atan(2/8)] ≈ [−15°, 15°]. However, the energy distribution for S 0 has its frequency- and direction-dependent anti-resonances. For a considerable frequency range [320, 420] KHz the maxima of power flow values are found to be in the direction φ = 60° instead of the normal focusing direction φ = 0°.The focusing properties of power flow for the SH 0 wave mode are much more complicated. The corresponding distribution (Fig. 13.7b) shows that for different values of frequency-thickness the main focusing direction is different. Its value changes from φ = 50° at 100 kHz to φ = 85° at 500 kHz.

Fig. 13.7
figure 7

Total through-thickness energy flow in dependence of φ and f calculated using AE in a quasi-isotropic [0/45/−45/90]2s plate with layers of IM7-Cycom977-3 under an excitation by an MFC source (A 1 = 8 mm, A 2 = 2 mm). Values of energy flow for r = 150 mm for S 0 (a) and for SH 0 (b) wave modes

Full size image

4 Conclusion

In this paper, displacements and the density of power flow excited in composite plates by harmonic surface-bonded sources of finite size are analyzed with the help of the residue theorem based on far-field residue integration technique (FFRIT) and of the asymptotic expansion (AE). Then, the application of these methods is studied using numerical examples. Results of computations show that these methods admit an efficient analysis of the directivity of the excitation source at different excitation frequencies and provide a tool for selective wave mode excitation and for the study of optimal design of the excitation source(s). Due to the complicated distributions of amplitudes and power flows in composite plates, such procedures are of great importance for the practical application of elastic waves for SHM systems and for the understanding of wave phenomena occurring in composites under excitation by piezoelectric sources.