A Framework for ODF Inference by Using Fiber Tract Adaptive MPG Selection

Abstract

The authors propose a method that selects a set of motion probing gradient (MPG) directions, which is adapted for measuring fiber tracts in some specific region of interest (ROI) with smaller number of MPGs. Given a training set of diffusion magnetic resonance (MR) images, the method selects the set of MPG directions by minimizing a cost function, which represents the square errors of the reconstructed oriented distribution functions (ODFs). This selection of MPGs is a combinatorial optimization problem, and a simulated annealing scheme is employed for selecting the MPGs. Experimental results demonstrated that the set of MPG directions selected by our proposed method reconstructed the ODFs more accurately than an existing method based on spherical harmonics and on greedy optimization.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

1.1 Background

High angular resolution diffusion imaging (HARDI ) is a powerful modality among diffusion MRI techniques, which are used for white matter fiber tractography. In HARDI, M different motion probing gradients (MPGs ) are iteratively applied while capturing a diffusion MR image, and a diffusion-weighted signal (DWS ) along the MPG direction is measured at all voxels at each iteration. Using a larger number of M, e.g. M = 256, one can measure diffusion MR images with higher angular resolution. The imaging, though, is more time consuming, when more MPG gradients are applied. It would take, e.g., more than 30 min to take one data set, when M = 256.

Many approaches, hence, have been proposed for shortening the imaging time[1, 2]. One of the main strategies for this time shortening is to capture images in a parallel manner[3–5]. The other main strategy is to reduce the number of MPG directions. The angular resolution is in general degraded, though, if you decrease the number of MPG gradients, M. One approach for suppressing this degrading is to use the framework of the compressed sensing[2, 6]. The other approach is to select a subset of M MPG directions, which is adapted for the measurements of some specific fiber tracts in brains[1]. Such the selection of tract-adaptive MPG directions is highly useful because an imaging target is often limited to a specific fiber tract structure with higher priority. Once the MPG directions are selected, you can improve also the parallel imaging methods by applying only the selected MPG directions. A structure of a specific fiber tract, of course, varies among patients, but the distribution of the directions of the fiber tract is anisotropic. The goal of the study is to obtain one set of MPG directions that is adaptive to each specific fiber tract of any patients. In this article, we propose a method that selects a set of MPG directions adaptive to a specific fiber tract, so that we can reconstruct the ODFs around the tract with less number of MPGs. The problem to be solved for this purpose is stated in the following section. It is a future work to obtain a set of MPG directions that is adaptive to any patients.

1.2 Problem Statement and Objective

Let a unit 3-vector, r _i $(i = 1,2,\cdots \,,M)$, denote the i-th MPG direction used in the HARDI, where M is the total number of the directions. Let $\varOmega _{M} =\{ r_{1},r_{2},\cdots \,,r_{M}\}$ denote a set of all of the MPG directions. Let a diffusion weighted signal (DWS) along r at the j-th spatial location be denoted by s ^j(r), where r is a 3-vector. The distribution of the diffusion coefficients at each spatial location can be represented by a continuous point-symmetry function defined on a unit sphere, and a HARDI measures the DWS along each sampling direction, r _i  ∈ Ω _M , defined on the hemisphere. Once one measures a set of the DWSs, $\{\tilde{{s}}^{j}(r_{i})\vert i = 1,2,\cdots \,,M\}$ at j, one can approximately obtain the continuous distribution of the strength by interpolating the measurements on the sphere.

Let assume that a subset of the MPG directions, Ω _m , is used for the measurements, where m = | Ω _m  | and 0 < m ≤ M, and that the continuous distribution is approximated by interpolating the measurements, $\{\tilde{{s}}^{j}(r_{i})\vert r_{i} \in \varOmega _{m}\}$. Let the approximation be denoted by $\hat{s}_{m}(r)$. The efficiency of the imaging is improved when a smaller number of the MPG directions, m, is used, but the angular resolution of $\hat{s}_{m}(r)$ decreases in general, and the resolution varies depending on the MPG directions included in Ω _m . It makes little sense to find the best combination of m MPG directions, if the distribution of the directions of fiber tracts is isotropic: You can just draw out randomly some of the MPG directions from Ω _M for determining Ω _m (m < M). It does make sense, though, to find the best one, if the distribution is anisotropic and is known in advance.

It was proposed in [1] to find the best set of the MPG directions adapted for measuring the structures of the pyramidal tracts (PYT ). In the method, the best subset, $\varOmega _{m}^{{\ast}}$, is determined by using a set of training data, $\mathcal{S} =\{\tilde{ {s}}^{j}(r_{i})\vert i = 1,2,\cdots \,,M,j = 1,2,\cdots \,,N_{\mathrm{P}}\}$, which are measured at N _P voxels in the pyramidal tracts of multiple cases. These training data are measured by using all of the M MPG directions, and the region of PYT in each measured image is labeled manually by an expert. The best subset, $\varOmega _{m}^{{\ast}}$, is obtained by minimizing the cost function shown below.

$$\displaystyle{ \varOmega _{m}^{{\ast}} =\arg \min _{\varOmega _{ m}}\sum _{j=1}^{N_{\mathrm{P}} }\sum _{i=1}^{M}\|\tilde{{s}}^{j}(r_{ i}) -\hat{ s}_{m}^{j}{(r_{ i})\|}^{2}. }$$

(1)

A set of spherical harmonics (SH ) is used for the interpolation, and a greedy strategy is employed for the minimization in [1]. In the followings, the method proposed in [1] is called as a SHG-method (Spherical harmonics and greedy). The objective of our study was to improve the SHG-method.

The first contribution of our study is that, instead of the DWS itself, the authors determine the best set by using the orientation distribution functions (ODF) in the proposed method. The ODF is commonly used for tracing fiber tracts and for analyzing their structures [7, 8]. Let $\hat{s}_{M}^{j}(r)$ denote a continuous function obtained by the interpolation of the measurements, $\{\tilde{{s}}^{j}(r_{i})\vert i = 1,2,\cdots \,,M\}$. Let $f_{M}^{j}(r)$ and $f_{m}^{j}(r)$ denote the ODFs obtained from $\hat{s}_{M}^{j}$ and $\hat{s}_{m}^{j}$, respectively. The proposed method determines the best set, $\varOmega _{m}^{\dag }$, by minimizing the following cost function (the exact definition of the cost will be shown later):

$$\displaystyle{ \varOmega _{m}^{\dag } =\arg \min _{\varOmega _{ m}}\sum _{j=1}^{N_{\mathrm{P}} }\sum _{i=1}^{M}\|f_{ M}^{j}(r_{ i}) - f_{m}^{j}{(r_{ i})\|}^{2}. }$$

(2)

It is not trivial to unveil if $\varOmega _{m}^{{\ast}}$ and $\varOmega _{m}^{\dag }$ are identical or not. The authors experimentally found that they are different, and believe that the ODFs should be employed for determining the subset of the MPG directions if one uses ODFs for the analysis.

The second contribution is that the method for the interpolation and for the minimization are improved in this study. The problems shown in (1) and (2) are the combinatorial optimizations, for which the greedy approach is too naive. The distributions of the MPG directions in Ω _m are non-uniform in general, and it is not easy to accurately interpolate the measurements without any aliasing errors, if you use the spherical harmonics. For the interpolation, we employ the spherical radial basis functions (SRBF ), which has a scale parameter, and the proposed method adaptively determines not only $\varOmega _{m}^{\dag }$ but also the value of the scale by minimizing the cost function. For the minimization, we applied two methods. In one method, we employed an approach used in a sparse PCA [9]: An approximated sparse solution of a relaxed original problem is obtained by using a lasso. In another method, we employed a simulated annealing. In this article, the latter method is described because it outperformed the former one.

2 Proposed Method

Given a set of the training data, $\mathcal{S}$, the proposed method obtains the subset of the MPG directions, Ω _m , that is appropriate for measuring the structures of PYT.

2.1 Interpolation with SRBF

In the proposed method, the spherical radial basis function (SRBF) is employed for interpolating the measured data, $\{\tilde{{s}}^{j}(r_{i})\vert r_{i} \in \varOmega _{m}\}$. The SRBF is defined as follows [10]:

$$\displaystyle{ \psi (t\vert \gamma ) = \frac{1} {\sqrt{1 {+\gamma }^{2 } - 2\gamma \cos t}},\;\;(0 <\gamma <1), }$$

(3)

where γ is the scale factor. Let $g(r_{i},r_{j})$ denote the geodesic distance between r _i and r _j on the unit sphere. Using SRBF, one can interpolate the measurements as follows:

$$\displaystyle{ \hat{s}_{m}^{j}(r) =\sum _{ r_{i}\in \varOmega _{m}}c_{i}\psi (g(r,r_{i})\vert \gamma ), }$$

(4)

where the coefficients, c _i , are uniquely determined based on the following constraints:

$$\displaystyle{ \hat{s}_{m}^{j}(r_{ i}) =\tilde{ {s}}^{j}(r_{ i}). }$$

(5)

The interpolated function, $\hat{s}_{m}^{j}(r)$, is defined on the unit sphere

2.2 Optimization

The cost function to be minimized is as follows, when you determine the MPG directions using the distribution of DWSs:

$$\displaystyle{ E_{\mathrm{DWS}}(\varOmega _{m},\gamma ) =\sum _{j}\sum _{i=1}^{M}\|\tilde{{s}}^{j}(r_{ i}) -\hat{ s}_{m}^{j}{(r_{ i})\|}^{2}. }$$

(6)

The cost function with the ODFs is as follows:

$$\displaystyle{ E_{\mathrm{ODF}}(\varOmega _{m},\gamma ) =\sum _{j}\sum _{i=1}^{M}\|f_{ M}^{j}(r_{ i}) - f_{m}^{j}{(r_{ i})\|}^{2}, }$$

(7)

where f _M ^j(r) and $f_{m}^{j}(r)$ are the ODFs obtained by applying the Funk-Radon transformation to the apparent diffusion coefficients (ADCs ) corresponding to $\hat{s}_{M}^{j}(r)$ and to $\hat{s}_{m}^{j}(r)$, respectively. In the proposed method, the cost functions are minimized by iteratively updating Ω _m and γ. The Metropolis sampling approach is used for the update.

At the k-th iteration ($k = 1,2,\cdots$) of the minimization process, one of the two propositions shown below is randomly selected, and the proposition is accepted with a probability, p _k . Let the temporal subset and the scale factor at the k-th iteration be denoted by $\varOmega _{m}^{(k)}$ and by γ ^(k).

Proposition I:

The scale factor, γ, is updated. ${\gamma }^{(k+1)} {=\gamma }^{(k)}+\epsilon$, where ε is a random variable, which obeys a uniform distribution, ε ∼ U(−Δ, Δ). The subset is not updated: $\varOmega _{m}^{(k+1)} =\varOmega _{ m}^{(k)}$. The positive value, Δ, is experimentally determined in advance.

Proposition II:

The subset, $\varOmega _{m}^{(k)}$, is updated. One MPG direction is selected from $\varOmega _{m}^{(k)}$ and from its complement, $\bar{\varOmega }_{m}^{(k)}$, and they are interchanged to obtain Ω _m ^(k+1). The scale factor is not updated: ${\gamma }^{(k+1)} {=\gamma }^{(k)}$.

The probability, p _k , is determined as

$$\displaystyle{ p_{k} =\min \left [1,\exp \left \{-\frac{E_{\mathrm{{\ast}}}(\varOmega _{m}^{(k+1)}{,\gamma }^{(k+1)}) - E_{\mathrm{{\ast}}}(\varOmega _{m}^{(k)}{,\gamma }^{(k)})} {{T}^{(k)}} \right \}\right ], }$$

(8)

where * denotes DWS or ODF, and T ^(k) is the temperature that is monotonically decreased while the iteration.

Annealing Minimization:

The training data set, $\mathcal{S}$, is input, and the optimizers of Ω _m and of γ are output.

• 1. Set the value of Δ and the values of ${T}^{(1)}> {T}^{(2)}> \cdots> {T}^{(K)}$, where K is the maximum number of the iteration.

• 2. Set k = 1, compute the initial subset of $\varOmega _{m}^{(1)}$, and set γ ⁽¹⁾ = 0. 5.

• 3. Randomly select one of the propositions, and temporally update to $\varOmega _{m}^{(k+1)}$ and γ ^(k+1).

• 4. Compute p _k , and accept $\varOmega _{m}^{(k+1)}$ and γ ^(k+1) with the probability p _k . If they are not accepted, reset as $\varOmega _{m}^{(k+1)} =\varOmega _{ m}^{(k)}$ and ${\gamma }^{(k+1)} {=\gamma }^{(k)}$.

• 5. Set $k \leftarrow k + 1$, and back to 3 until it converges or k > K.

• 6. Output Ω ^(k) and γ ^(k) as the optimizers.

The initial subset, Ω _m ⁽¹⁾, is obtained by using a greedy minimization method. Let $\varOmega _{n\setminus i} =\varOmega _{n}\setminus r_{i}$, where $r_{i} \in \varOmega _{n}$.

Greedy Minimization:

The training data set, $\mathcal{S}$, is input, and $\varOmega _{m}^{(1)}$ is output.

• 1. Set γ = 0. 5 and set n = M.

• 2. Compute a MPG direction, $r_{{i}^{{\ast}}} \in \varOmega _{n}$ where ${i}^{{\ast}} =\arg \min _{i}\left (E_{\mathrm{{\ast}}}(\varOmega _{n\setminus i},\gamma )-\right.$ $\left.E_{\mathrm{{\ast}}}(\varOmega _{n},\gamma )\right ).$

• 3. Set $n \rightarrow n - 1$ and back to 2 if n > m.

• 4. Output Ω _m .

2.3 Preprocessing

Our method applies a bilateral filter  [11] to given training images to eliminate measurement noises. As mentioned above, all measured points, $\{(r_{i},\tilde{{s}}^{j}(r_{i}))\vert r_{i} \in \varOmega _{m}\}$, are located on the graph of $\hat{{s}}^{j}(r)$. In other words, measurement noises are also reconstructed by the interpolation. A bilateral filter computes the weighted averages of given images as follows:

$$\displaystyle{ \tilde{{s}}^{j}(r_{ i}) \leftarrow \frac{1} {Z}\sum _{u}w_{d}(j,u)w_{s}(j,u)\tilde{{s}}^{u}(r_{ i}), }$$

(9)

where Z is a normalization coefficient. Let the Euclid distance between the voxels, j and u, be denoted by d(j, u). Then the weights, w _d (j, u) and w _s (j, u), are determined as follows:

$$\displaystyle{ w_{d}(j,u) =\exp \{ -\lambda _{1}{d}^{2}(j,u)\},\mbox{ and }w_{ s}(j,u) =\exp \{ -\lambda _{2}\|\tilde{{s}}^{j}(r_{ i}) -\tilde{ {s}}^{u}{(r_{ i})\|}^{2}\}.\quad }$$

(10)

The values of the coefficients, λ ₁ and λ ₂, are experimentally determined.

3 Experimental Method

The performance of the proposed method was compared with that of the SHG-method, which minimizes the following cost function:

$$\displaystyle{ E_{\mathrm{DWS}}^{{\prime}}(\varOmega _{ m}) =\sum _{j}\sum _{i=1}^{M}\|\tilde{{s}}^{j}(r_{ i}) -\hat{ s}_{m}^{j}{(r_{ i})\|}^{2}. }$$

(11)

The difference between E _DWS ^′ and E _DWS in (6) is their arguments: The arguments of $E_{\mathrm{DWS}}^{{\prime}}$ do not include γ, becausethe spherical harmonics (SH) are used for the interpolation of the measurements. Let a m-vector, $\tilde{{s}}^{j} = {[\cdots \,,\tilde{{s}}^{j}(r_{i}),\cdots \,]}^{T}$ (r _i  ∈ Ω _m ), denote the measurements obtained using the MPGs in Ω _m . For obtaining the continuous function, $\hat{s}_{m}^{j}(r)$, the SHG-method interpolates the measurements by projecting $\tilde{{s}}^{j}$ to a subspace, which is spanned by a set of spherical harmonics with lower frequencies. The projection is computed with a L2-regularization. It should be noted that this projection smooths the functions and reduces the measurement noises. The bilateral filtering is, hence, not required.

The greedy algorithm shown in the previous section is used for minimizing $E_{\mathrm{DWS}}^{{\prime}}(\varOmega _{m})$. Once SHG-method obtains the subset of the MPG directions, Ω _m ^∗, then you can compute the ODF, $f_{m}^{j}(r)$, from $\hat{s}_{m}^{j}(r)$.

3.1 Simulation Experiments

Artificial diffusion images were firstly used for comparing the performances between the proposed method and the SHG-method. Setting M = 256 and distributing r _i uniformly on the unit sphere, we firstly generated a set of artificial DWSs using the following equation:

$$\displaystyle{ {s}^{j}(r_{ i}) = s_{0}^{j}\sum _{ l=1}^{{L}^{j} }\alpha _{l}^{j}\exp \{ - b(r_{ i}^{T}T_{ l}^{j}r_{ i})\}, }$$

(12)

where L ^j is the number of fiber tracts at the j-th voxel and α _k determines the mixture proportion of the tracts. $T_{l}^{j} = \mbox{ diag}(1.7,0.3,0.3) \times 1{0}^{-3}$ if fiber tracts exist at the voxel, j. We set b = 1, 500 s/mm² and s ₀ = 10 in the simulation. Then, we added Rician noises to s ^j(r _i ) to obtain the artificial measurements, $\tilde{{s}}^{j}(r_{i})$.

$$\displaystyle{ \tilde{{s}}^{j}(r_{ j}) = \sqrt{{\left ({s}^{j } (r_{i } ) \right ) }^{2 } +{ \left (\mathcal{N}(0{,\sigma }^{2 } ) \right ) }^{2}}, }$$

(13)

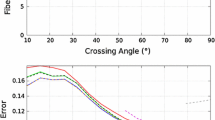
where $\mathcal{N}(0{,\sigma }^{2})$ is a Gaussian, of which the mean is zero and the variance is σ ². We generated a set of artificial diffusion images, of which size was 15 × 15 × 1. Two fiber tracts cross together in each of the images as shown in Fig. 1a. The two tracts cross with 85^∘ at the center of the image, and the corresponding mixture proportion, α ₁:α ₂ = 0.5:0.5. Fixing ${s}^{j}(r_{i})$ and adding the random Rician noises, we generated one set of training images and a set of test ones. Varying the Rician noise level and the structure of the fiber tracts, ${s}^{j}(r_{i})$, we generated multiple sets of training data and test ones. Figure 1b shows an example of the ADC generated at the intersection of the two tracts. An example of the corresponding ODF is shown in Fig. 1c. The blue axes shown in the figure indicate the directions of the fiber tracts at the voxel.

Fig. 1

(a): The distribution of the fiber tract directions in the artificial diffusion images. (b): An ADC profile observed at the cross point. (c): The ODF corresponding to (b). (d): The SRBF with different values of γ. (e): Fiber cup image. (f): Region of interest

The performances were quantitatively evaluated using not only the value of E _ODF in (7) but also the locations of the local maxima of the reconstructed ODFs. Let $\bar{r}_{l}^{j}$ $(l = 1,2,\cdots {L}^{j})$ denote the gold standard of the fiber tract directions at the j-th voxel, and let $\hat{r}_{l}^{j}$ denote the local maximum of the ODF closest to $\bar{r}_{l}^{j}$. The distribution of $\delta _{l}^{j} =\hat{ r}_{l}^{j} -\bar{ r}_{l}^{j}$ was evaluated, because the local maxima of ODFs are often detected in tractography for estimating the directions of fiber tracts. $\delta _{l}^{j}$ becomes closer to zero, when the local maximum is more reliable.

3.2 Phantom Experiments

A phantom data, Fiber cup  [12], was then used for evaluating the performances of the methods. One of the advantages of using phantom data is that the gold standard of the fiber tracts structures in the image is available. Figure 1e shows the image. A ROI was manually labeled as shown in Fig. 1f. The subsets, $\varOmega _{m}^{{\ast}}$ and $\varOmega _{m}^{\dag }$, were computed from the measurements in the ROI of the Fiber cup image. In addition, randomly selecting m MPG directions from the M = 64 ones, we obtained another subset, $\varOmega _{m}^{\bullet }$. Using these subsets of MPG directions, we reconstructed the ODFs, $f_{{m}^{{\ast}}}^{j}$, $f_{{m}^{\dag }}^{j}$, and $f_{{m}^{\bullet }}^{j}$ for each voxel in the ROI, respectively. The RMS errors between the gold standard, $f_{M}^{j}(r)$, and the reconstructed ones were evaluated as shown in (7). In addition, we verified if the subset, $\varOmega _{m}^{\dag }$, was adapted for measuring the fiber tract structures of a ROI. Another subset, $\varOmega _{m}^{\ddag }$, was computed by the proposed method not from the ROI but from the whole tract regions in the image. The ODF, $f_{{m}^{\ddag }}^{j}$, were reconstructed for each voxel in the ROI, and its RMS error was evaluated for comparing that of $f_{{m}^{\dag }}^{j}$.

3.3 Clinical Image Experiments

Clinical four diffusion weighted images (DWI) captured by a Siemens 1.5T scanner (Avanto) were used for the performance evaluation. The b-value was 1,000 s/mm². The spatial resolution was 3 mm, the total number of the MPG directions, M, was 256, and TR and TE were 5,000 and 97 ms, respectively. We manually labeled the left PYT region in each of the DWIs. The number of the labeled voxels was about 1,500 in each DWI. Leave-one-case-out cross validation was applied for the performance evaluation. The RMS errors of the reconstructed ODFs were evaluated in an analogous way described above.

4 Experimental Results

4.1 Simulation Experiments

The graph shown in Fig. 2a shows the RMS errors. In the graph, the x-axis shows the number of the MPG directions, m, and the y-axis shows the RMS. As shown in the graph, the subset, Ω _m ^†, selected by the proposed method reconstructed the ODFs more accurately than Ω _m ^∗ selected by the SHG-method. The Wilcoxon signed-rank test showed that the difference between the RMS errors that correspond to $\varOmega _{m}^{\dag }$ and to Ω _m ^∗ was statistically significant at p < 0. 05.

The proposed method can select not only the m MPG directions but also the appropriate scale factor for the SRBF, γ. The selected scale factor decreased as m increased, as shown in Fig. 2b. In other words, more narrow SRBF was selected for interpolating more dense measurements. The SRBFs with different values of γ are shown in Fig. 1c. In the figure, the blue, green, and the red curves correspond to γ = 0. 6, 0.5, and 0.4, respectively. Examples of the reconstructed ODFs are shown in Fig. 2d, e. Both results were obtained when m = 30. In the figures, the red points indicate the local maximum points. The ODF shown in (e) was obtained by the SHG-method and that in (f) was obtained by the proposed method. The latter one had higher angular resolution. They were obtained at the identical voxel with the ODF shown in Fig. 2c, which was computed from the original signals.

Fig. 2

(a): The relationships between m and the RMS errors in artificial images. Red: SHG-method, Blue: Proposed method. (b): The change of γ in Eq. (3) with respect to m. (c): An example of the ODF computed from the original signal measured at the intersection between two tracts. (d): The ODF reconstructed by SHG-method. (e): The ODF by the proposed method

Fig. 3

Examples of the distributions of δ _l ^j, which represents the error of the estimated fiber tract direction. (a) The SHG-method. (b) The proposed method

The graphs indicated in Fig. 3 show some examples of the distributions of $\delta _{l}^{j} =\hat{ r}_{l}^{j} -\bar{ r}_{l}^{j}$ obtained at the intersection point of the two fiber tracts. Let Π denote the plane spanned by the two tracts near the intersection point. The x axis of each graph denotes the error in Π, and the y axis denotes the error along the direction perpendicular to Π. The distribution localizes on the origin (the center of the graph), when the local maximum accurately locates at the fiber tract direction. As shown in the figure, the distribution of δ _l ^j was widely spread when the SHG-method was used. When the proposed method was used, on the other hand, the local maxima were extracted near the correct tract direction.

Fig. 4

(a) The relationships between m and the RMS errors in phantom images. Green: Random selection, Red: SHG-method, Blue: Proposed method. (b) The RMS errors of $f_{{m}^{\dag }}^{j}(r)$ (blue) and of $f_{{m}^{\ddag }}^{j}(r)$ (red). (c) The ROIs set by manually labeling the pyramidal tracts. (d) The relationships between m and the RMS errors in clinical images. Red: SHG-method, Blue: Proposed method

4.2 Phantom Experiments

The RMS errors of the ODFs were evaluated for $\varOmega _{m}^{{\ast}}$, $\varOmega _{m}^{\dag }$, and $\varOmega _{m}^{\bullet }$. The random selection of the MPG directions for $\varOmega _{m}^{\bullet }$ was iterated 100 times, and the RMS error was evaluated at each iteration for estimating the statistical distribution of the RMS errors. The graph shown in Fig. 4a shows the results. In the graph, x-axis shows the value of m and the y-axis shows the RMS errors. The green, red, and blue graphs indicate the results obtained from $\varOmega _{m}^{\bullet }$, $\varOmega _{m}^{{\ast}}$, and $\varOmega _{m}^{\dag }$, respectively. The vertical bars in the green graph shows the range of ±σ. The MPG directions selected by the proposed method reconstructed the ODFs most accurately.

The graph shown in Fig. 4b shows the RMS errors of $f_{{m}^{\dag }}^{j}$ and $f_{{m}^{\ddag }}^{j}$ evaluated using the identical set of voxels in the image. As shown by the graph, the RMS errors of $f_{{m}^{\dag }}^{j}$ were smaller than that of $f_{{m}^{\ddag }}^{j}$. The Wilcoxon signed-rank test showed that the difference of the RMS errors was statistically significant at p < 0. 05. This results mean that the subset of the MPG directions adapted for the ROI is successfully obtained by the proposed method.

4.3 Clinical Image Experiments

Labelling the pyramidal tracts, we set the ROI as shown in Fig. 4c. The measurements in the ROI were used as the training set. The resultant graph of the RMS errors are shown in Fig. 4d. As shown in the graph, the subset of the MPG directions computed by the proposed method reconstructed the ODFs in the PYT more accurately than that computed by SHG-method. The Wilcoxon signed-rank test showed that the difference of the RMS errors was statistically significant at p < 0. 05.

5 Conclusion

A new method is proposed that selects a subset of MPG directions, which is adapted for measuring fiber tracts in some specific ROI. The method interpolates the non-uniformly sampled measurements using SRBF, and selects the subset based on the accuracy of the reconstructed ODFs. The selection of the MPG directions is combinatorial optimization problem, and a simulated annealing approach is employed for solving it. Experimental results with artificial images, phantom ones, and clinical ones demonstrated that the proposed method can select the subset that can reconstruct the ODFs more accurately than the existing SHG-method. Future works include to improve the optimization algorithm, and to apply the proposed method to more clinical images for evaluating the performance. As mentioned above, it is a future work to obtain a set of MPG directions that is adaptive to any patients. Applying the proposed method to training data obtained from many patients, you would be able to select such the set of MPG directions.