Keywords

1 Introduction

A definition of economic dispatch is the operation of generation facilities to produce energy at the lowest cost to reliably serve consumers, recognizing any operational limits of generation and transmission facilities.

An electric network consists of many generation nodes with various generating capacities and cost functions, lines of transmission and nodes of power demand. The MOED problem is made up by unit commitment problem [1] and optimal power flow that is seen as an economic dispatch (ED) [2–4]. Both subproblems have been studied for many years and there are many algorithms to found good solutions with different complexity. Most of the authors consider both problems separately. In the typical unit commitment (UC), the transmission network is not considered and in ED, the transmission network is modeled in but only a single time period is considered.

Since the MOED problem is a NP-hard MINLP, for large power systems, it is extremely difficult to obtain the exact optimal solution [1]. Because of this, we present an alternative to solve a MOED based on a generalized cross decomposition (GCD) [5] strategy in order to reduce the computational effort.

This decomposition simultaneously utilizes primal and dual subproblems by exploiting the advantages of lagrangean relaxation [6] and generalized benders decomposition (GBD) [7]. The practical motivation of Cross Decomposition is to replace the hard primal master problem with the easier dual subproblem to the largest possible extent.

The proposed decomposition strategy shows good convergence properties for this application, the number of iterations required to attained convergence is typically low, so the computation time is less.

2 Problem Description

MOED problem is defined as determining the mix of generators and their estimated output level to meet the expected demand of electricity over a given time horizon (a day or a week), while satisfying the load demand, spinning reserve requirement and transmission network constraints.

In this work we addresses a MOED problem based on [8] notation, where network constraints are represented through a DC model [2] and considers a multiperiod time horizon.

2.1 Nomenclature

Constants

\( A_{j} \) :

Start up cost of power plant \( j \)

\( B_{nm} \) :

Susceptance of line \( n - m \)

\( C_{nm} \) :

Transmission capacity limit of line \( n - m \)

\( D_{nk} \) :

Load demand at node \( n \) during period \( k \)

\( E_{j} (t_{jk} ) \) :

Nonlinear function representing the operating cost of power plant \( j \) as a function of its power output in period \( k \)

\( E_{j1} \) :

Linear coefficient of operating cost for the plant \( j \)

\( E_{j2} \) :

Quadratic coefficient of operating cost for the plant \( j \)

\( F_{j} \) :

Fixed cost of power plant \( j \)

\( V_{jk} \) :

Parameter which is equal to 1 when plant \( j \) is committed in period k after dual subproblem is solved in \( \varphi \) iteration

\( Y_{jk} \) :

Parameter which is equal to 1 when plant \( j \) is started up at the beginning of period k after dual subproblem is solved in \( \varphi \) iteration

\( K_{nm} \) :

Conductance of line \( n - m \)

\( R_{k} \) :

Spinning reserve requirement during period \( k \)

\( \overline{{T_{j} }} \) :

Maximum power output of plant \( j \)

\( \underline{{T_{j} }} \) :

Minimum power output of plant \( j \)

\( nr \) :

Reference node with angle cero

Variables

\( t_{jk} \) :

Power output of plant \( j \) in period \( k \)

\( v_{jk} \) :

Binary variable, which is equal to 1 when plant \( j \) is committed in period

\( y_{jk} \) :

Binary variable, which is equal to 1 when plant \( j \) is started up at the beginning of period \( k \)

\( \delta_{nk} \) :

Angle of node \( n \)in period \( k \)

\( \lambda_{nk} \) :

Lagrangean multiplier associated to a power balance constraint

\( \mu_{k} \) :

Lagrangean multiplier associated to a spinning reserve requirement

\( \gamma_{nk} ,\beta_{nk} \) :

Lagrangean multipliers associated to transmission capacity limits

Sets

J :

Set of indices of all plants

K :

Set of period indices

N :

Set of indices of all nodes

\( \Uplambda_{n} \) :

Set of indices of the power plants j at node n

\( \Upomega_{n} \) :

Set of indices of nodes connected and adjacent to node n

\( \Upphi \) :

Set of Generalized Cross Decomposition iterations

The objective is minimises a function that includes fixed cost, start up cost and operating cost. A second order polynomial describes the variable costs as a function of the electric power.

$$ Min\,Z = \sum\limits_{k \in K} {\sum\limits_{j = J} {[F_{j} v_{jk} + A_{j} y_{jk} + E_{j} (t_{jk} )]} } $$
(1)

There is a power balance constraint per node and time period. In each period, the production has to satisfy the demand and losses in each node. Line losses are modeled through cosine approximation and it is assumed that the demand for electric energy is known and is discretized into t periods.

$$ \begin{aligned} &{\sum\limits_{{j \in \lambda_{n} }}^{{}}{t_{jk} + \sum\limits_{{m \in \omega_{n} }}^{{}} {B_{nm}[\delta_{mk} - \delta_{nk} ]} } - \sum\limits_{{m \in \omega_{n}}} {K_{nm} [1 - \cos (\delta_{mk} - \delta_{nk} } )] = D_{nk} \, }\\ &{\forall n \in N,\forall k \in K} \\ \end{aligned} $$
(2)

Spinning reserve requirements are modeled. In each period the running units have to be able to satisfy the demand and the prespecified spinning reserve.

$$ \sum\limits_{j \in J} {\overline{{T_{j} }} v_{jk} } \ge \, \sum\limits_{{{\text{n}} \in {\text{N}}}} {{\text{D}}_{\text{nk}} + R_{k} } \quad \forall k \in K $$
(3)

Each unit has a technical lower and upper bound for the power production.

$$ \underline{{T_{j} }} v_{jk} \le t_{jk} \le \overline{{T_{j} }} v_{jk} \quad \forall j \in J,\forall k \in K $$
(4)

Transmission capacity limits of lines avoid dynamic stability system problems.

$$ - C_{nm} \le B_{nm} [\delta_{mk} - \delta_{nk} ] \le C_{nm} \quad \forall n \in N,\forall k \in K,\forall m \in \Upomega_{n} $$
(5)

This constraint holds the logic of running, start-up and shut-down of the units. A running unit cannot be started-up.

$$ y_{jk} \ge v_{jk} { - }v_{jk - 1} \quad \forall j \in J,\forall k $$
(6)

Angle in all buses has a lower and upper bound.

$$ - \pi \le \delta_{nk} \le \pi \quad \forall n \in N/\left\{ {nr} \right\},\forall k \in K $$
(7)

3 Solution Approach

Because the MOED is a MINLP Np-hard problem, there is an exponential increase in solution time with the number of time periods as well as with the number of generation nodes. Therefore, in order to solve this problem in better solution time than other methods, we apply GCD strategy.

The basic GCD [5] consists of two phases, that is the primal and dual subproblem phase (phase I), and the master problem phase (phase II), and appropriate convergence tests. In phase I the primal subproblem provides an upper bound of the optimal solution for the MOED (1-7) and lagrange multipliers for the dual subproblem. The dual subproblem provides lower bound on the solution of MOED and supplies binary variables for the primal subproblem.

Both, the primal and the dual subproblem generate cuts for the master problem in phase II. At each iteration of the GCD, primal and dual subproblems are solved, and a primal convergence test is applied on binary variables, while a dual convergence test is applied on lagrange multipliers. If any convergence test fails, then we enter phase II that features the solution of master problem and return subsequently to phase I. The convergence tests of the GCD provide information about an upper bound improvement and a lower bound improvement. Upper bound improvement corresponds to a decrease in the upper bound obtained by the primal subproblem. A lower bound improvement corresponds to an increase in the lower bound obtained by the dual subproblem.

In this work we present a strategy for the implementation of the GCD that avoid the use of master problem. This is because the master problem is known to be a more difficult and cpu time consuming problem, than the primal and dual subproblems of phase I. The key idea is to make extensive use of phase I (primal and dual subproblems). For this, we use a MINLP and NLP solvers to solve primal and dual subproblems respectively. These solvers ensure the convergence of each subproblem solution in less time than the solution of master problem.

Therefore, the MOED is divided into one primal problem (9) and one dual subproblem (8), which is a classic economic dispatch. The algorithm initialized with a set of lagrange multipliers, which are defined heuristically as a result of the knowledge of the original problem. Then, the dual subproblem is solved and provides integer variables for the primal subproblem and a lower bound of the original problem (MOED) in the \( \varphi \) iteration of GCD.

Later, the primal subproblem is solved and provides the lagrangean multipliers (that are fixed in the next dual subproblem) and an upper bound for the MOED problem in the \( \varphi \) iteration of GCD.

To conform the dual subproblem we used a nodal decomposition of the original problem [9] to relax the system constraints power balance (2), spinning reserve (3) and transmission capacity limits of lines (5). Dualizing these constraints produces a dual subproblem that is less expensive to solve and speed up the solution of this subproblem.

A primal convergence test and dual convergence test are used to check a bound improvement and to verify when an optimal solution is reached. We describe the dual subproblem and primal subproblem for MOED.

Dual subproblem

$$\begin{aligned} & \mathop {\hbox{min} }\limits_{{t_{jk} ,v_{jk},y_{jk} ,\delta_{nk} }} D_{sub}^{\varphi } \Big \{ \sum\limits_{k \in K}{\sum\limits_{{j \in \lambda_{n} }} {[F_{j} v_{jk} + A_{j} y_{jk}+ E_{j} (t_{jk} )]} } \\ & + \sum\limits_{k \in K} {\lambda_{k}\Big[D_{nk} - } \sum\limits_{{j \in \lambda_{n} }} {t_{jk} } -\sum\limits_{{m \in \omega_{n} }} {B_{nm} (\delta_{mk} -\delta_{nk} )} + \sum\limits_{{m \in \omega_{n} }} {K_{nm} (1 -\cos (\delta_{mk} - \delta_{nk} } )\Big] \\ & + \sum\limits_{k \in K}{\mu_{k} \Big[D_{nk} + R_{k} - } \sum\limits_{j \in J} {\overline{{T_{j}}} v_{jk} }\Big ] + \sum\limits_{k \in K} {\gamma_{k} \Big[C_{nm} - }\sum\limits_{{m \in \omega_{n} }} {B_{nm} (\delta_{mk} -\delta_{nk} )} \Big] \\ & + \sum\limits_{k \in K} {\beta_{k}\Big [ - }\sum\limits_{{m \in \omega_{n} }} {B_{nm} (\delta_{mk} -\delta_{nk} )} - C_{nm}\Big ] \, \Big \} \\ \end{aligned}$$
(8)

subject to constraints (2), (4) and (6).

Primal subproblem

$$ \begin{array}{*{20}l} {\mathop {Min}\limits_{{t_{jk} ,\delta_{nk} }} P_{sub}^{\varphi } = \sum\limits_{k \in K} {\sum\limits_{j = J} {[E_{j} (t_{jk} )]} } } \hfill \\ {subject \, to:} \hfill \\ {\sum\limits_{{j \in \Uplambda_{n} }} {t_{jk} + } \sum\limits_{{m \in \Upomega_{n} }} {B_{nm} [\delta_{mk} - \delta_{nk} ]} \, - \sum\limits_{{m \in \Upomega_{n} }} {K_{nm} [1 - \cos (\delta_{mk} - \delta_{nk} } )] = D_{nk} } \hfill \\ {\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \forall n \in N,\forall k \in K} \hfill \\ {\underline{{T_{j} }} v_{jk} \le t_{jk} \le \overline{{T_{j} }} v_{jk} \quad \forall j \in J,\forall k \in K} \hfill \\ { - C_{nm} \le B_{nm} [\delta_{mk} - \delta_{nk} ] \le C_{nm} \quad \forall n \in N,\forall k \in K,\,\forall m\,\Upomega_{n} } \hfill \\ { - \pi \le \delta_{nk} \le \pi \quad \forall n \in N/\{ nr\} ,\forall k \in K} \hfill \\ {v_{jk} = V_{jk}^{\varphi } } \hfill \\ {y_{jk} = Y_{jk}^{\varphi } } \hfill \\ \end{array} $$
(9)

In all cases available solution data include total generation costs, on/off status of every thermal unit per hour, power output of every plant per hour, angle of every node per hour.

4 The Computational Tool

Two test systems are presented to evaluate the performance of the proposed decomposition strategy. The IEEE 24 bus test system with 24 nodes, 24 thermal units and 38 transmission lines [10], and a portion of bus electric energy system of Mainland Spain with 104 nodes, 62 thermal units and 160 transmission lines [8].

The mathematical model of MOED and the decomposition strategy were implemented in GAMS [11] using the solver DICOPT [12] for solving the MINLP problems (dual subproblems).

DICOPT solves a series of NLP and MIP subproblems. These subproblems can be solved using any NLP or MIP solver that runs under GAMS, for this case we use CONOPT [13] for solving the NLP problems (primal subproblems) and CPLEX 12 [14] for MIP problems. All the models have been solved on an AMD Phenom ™ II N970 Quad-Core with a 2.2 GHz processor and 8 GB RAM.

5 Results

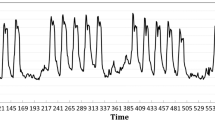
The graphics in the Figs. 1 and 2 show GCD iterations were needed to solve IEEE 24 bus test system, and 104 nodes system. E-optimum corresponds to optimal value of the full scale model (MOED) obtained directly with DICOPT solver. Additionally, the graphics present total CPU time required for solving two test systems. We compared direct solution with DICOPT true GAMS with the GCD strategy. The decomposition strategy proposed yield better solutions to the addressed problem (Table 1).

Fig. 1
figure 1

Generalized cross decomposition of the IEEE 24 bus test system

Full size image
Fig. 2
figure 2

Generalized cross decomposition of the 104 nodes electric energy system of Mainland Spain

Full size image
Table 1 Solution time results obtained by generalized cross decomposition strategy and by DICOPT solver
Full size table

6 Conclusions

Several works revealed that the computational effort of multiperiod optimal economic dispatch models grows exponentially with the number of time periods and nodes. Therefore, in order to reduce the computational effort of the problem special techniques must be employed. The proposal was to apply generalized cross decomposition strategy, which exploits the structure of the problem, to reduce solution time by decomposing the model (MOED). It was not necessary to solve a master problem since in the subproblem phase, NLP and MINLP solvers were tuned to obtain solutions with a 10 % of optimality. In case the primal subproblem (NLP subproblem) are very difficult, using a combination of NLP solvers under GAMS has been found to be effective. The solution of proposed strategy showed a significant reduction in computational effort with respect to the full-scale MINLP solver.