A Three-Dimensional SPH Approach for Modelling the Collision Process Between Liquid Drops: The Formation of Clusters of Unequal-Sized Drops

Abstract

In this chapter, we present three-dimensional simulations of the coalescence collision and clustering of unequal-sized water drops in vacuum, using the method of Smoothed Particle Hydrodynamics (SPH). The thermodynamics of the problem is represented by a Mie-Grüneisen equation of state. Depending on the magnitude of the collision velocity three different outcomes are observed: permanent coalescence, permanent coalescence accompanied by fragmentation into satellite droplets, and drop clustering with no coalescence (flocculation). When the inertial forces prevail and the surface tension forces are too low permanent coalescence with or without fragmentation into satellite droplets is observed, but for low collision velocities of 0.5 mm/ms, or less, the simulations predict drop flocculation. In this latter case, the drops remain attached to one another, forming a drop clustering.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

The study of the coalescence collision of liquid drops has important natural and industrial applications as, for example, in emulsification, combustion of fuel sprays, spray coating, waste treatment, and raindrop formation among many others. The coalescence of liquid drops has been studied extensively both numerically and experimentally. However, most existing numerical simulations have considered binary drops in two-space dimensions or, in the best case, constrained by axi-symmetry (Foote 1974; Chen 1985; Li 1994; Nobari et al. 1995; Eow and Ghadiri 2003a, b; Mashayek et al. 2003; Meleán and Sigalotti 2005).

A first attempt to simulate head-on collisions of equal-sized drops for small Weber numbers (We $<$ 5) was reported by Foote (1974). The occurrence of bouncing and permanent coalescence from the head-on collision of binary drops was further investigated by Nobari et al. (1995). In more recent times, the coalescence produced by the collision of axi-symmetric binary drops was simulated by Mashayek et al. (2003), who investigated the effects of varying Reynolds numbers, impact velocity, drop size ratio, and internal circulation on binary coalescence for low Weber numbers ($\approx$1). These calculations were extended to off-centre collisions of binary drops by Meleán and Sigalotti (2005), using Smoothed Particle Hydrodynamics (SPH). On the other hand, Chen (1985) and Li (1994) studied the coalescence of two small bubbles or drops using a model for the dynamics of the film thinning behaviour, in which both London-van der Waals and electrostatic double-layer forces are taken into account. In particular, the model proposed by Chen (1985) describes the film profile evolution and predicts the film stability, timescale, and film thickness, depending on the radius of the drops and the physical properties of the fluids and surfaces, while Li (1994) proposed a general expression for the coalescence time in the absence of the electrostatic double-layer forces.

Experimental studies of the binary collision of alkane droplets were carried out by Ashgriz and Givi (1987, 1989). They found that for near head-on collisions with increasing We, the impact can result in permanent coalescence, bouncing, and permanent coalescence again followed by reflexive separation into two or more drops. As We is further increased, reflexive separation may result in a string of three or more drops, whereas for very high impact velocities the collision may result in shattering separation in which the colliding drops disintegrate into a cluster of much smaller droplets. Similar experimental studies of binary collision of equal-sized alcohol droplets were carried out by Brenn and Frohn (1989). Ashgriz and Poo (1990) conducted experimental studies of the off-centre and grazing binary collision of water droplets for a wide range of We and impact parameters. In general, they found permanent coalescence and bouncing at low and moderate We, reflexive separation for higher We and low impact parameters ($\le$0.4), and stretching separation for both higher We and higher impact parameters. The collision of equal-sized water and normal-alkane drops for $1 \le \mathrm{We} \le 100$ and radius of 0.1 mm have also been studied experimentally by Jiang et al. (1992). Although different fluids were used, these experiments were quite similar to those conducted by Ashgriz and Poo (1990). However, there was a discrepancy in the experimental observations on head-on collisions of water drops between the two studies. In the former case permanent coalescence was always observed, while in the latter experiments reflexive separation was observed.

Fig. 1

Time sequence showing the evolution of the collision of four drops (permanent coalescence) with $\mathrm{V}_{\text {col}}=15.0\,\text {mm/ms}$. Time is given in milliseconds. The origin of the coordinate system coincides with the centre of each panel

In the petroleum refineries, coalescence of fine oil mist is sometimes attained using electric fields to break up the emulsions. With this in mind, Eow and Ghadiri (2003a) investigated the behaviour of a liquid-liquid interface and drop-interface coalescence under the influence of an electric field. The measurement of the electric current can be used to monitor and control the behaviour of a liquid-liquid interface, thus providing an optimum condition for instantaneous and single-staged drop-interface coalescence. In a companion chapter, Eow and Ghadiri (2003b) studied the effects of the direction of the applied electric field as well as the geometry of the electrodes. From this study it follows that the premature drop-drop coalescence in an electric field is influenced by the natural mechanical vibration and cavitation within the drops.

Recent numerical simulations by Acevedo-Malavé and García-Sucre (2011a, b, c, 2012) considered the coalescence process of liquid drops in three-space dimensions, using SPH methods. For binary drop collisions, they found that depending on the impact velocity three possible outcomes may arise: drop flocculation, in which the drops remain attached without fragmenting, for low impact velocities; permanent coalescence into a bigger drop; and permanent coalescence with fragmentation into satellite droplets for higher impact velocities. In this chapter, we extend these previous simulations to multiple collisions of unequal-sized drops, where smaller drops are made to collide with a bigger one for impact velocities in the range $0.5 \le \mathrm{V}_{\text {col}} \le 30\,\text {mm/ms}$.

Fig. 2

Velocity vector field during the collision of four drops at ${ t} = 1.5\times 10^{-4}\,\mathrm{ms}$ (permanent coalescence) with $\mathrm{V}_{\text {col}} = 15.0\,\text {mm/ms}$

Fig. 3

Time sequence showing the evolution of the collision of four drops (fragmentation) with $\mathrm{V}_{\text {col}}=30.0\,\text {mm/ms}$. Time is given in milliseconds. The origin of the coordinate system coincides with the centre of each panel

Fig. 4

Velocity vector field for the collision of four drops with $\mathrm{V}_{\text {col}}=30.0\,\text {mm/ms}$ (permanent coalescence with fragmentation) at ${ t}=8.7\times 10^{-5}\,\mathrm{{ms}}$

Fig. 5

Time sequence showing the evolution of the collision of four drops with $\mathrm{V}_{\text {col}}=0.5\,\text {mm/ms}$ (flocculation). Time is given in milliseconds. The origin of the coordinate system coincides with the centre of each panel

Fig. 6

Velocity vector field for the collision of four drops at ${ t}=7.2\times 10^{-3}\,\mathrm{{ms}}$ with $\mathrm{V}_{\text {col}}=0.5\,\text {mm/ms}$ (flocculation)

2 Basic Formulation and Numerical Methods

Here, we present only a brief description of the method, and refer the reader to Acevedo-Malavé and García-Sucre (2011a, b, c, 2012) for more details. SPH is a fully Lagrangian particle method used for simulations of discontinuous flows with large deformations (Monaghan 1985). It solves the laws of mass, momentum, and energy conservation.This equations are discretized through the use of an interpolating kernel function W that gives the estimate of the field variables at a set of particles suitably chosen to represent the fluid elements (Monaghan 1985). In practice, the mean value $A_{s}(\mathbf{r})$ of a function A(r) is expressed by the convolution integral of the exact function with the kernel interpolant so that

$$\begin{aligned} A_{s} \left( \mathbf{r } \right) = \int A\left( \mathbf{r } \right) W\left( \mathbf{r }\, - \mathbf{r }^{\prime } ,h \right) d\mathbf{r }^{\prime }, \end{aligned}$$

(1)

where the integration is performed over all space and h is the smoothing length which determines the spatial resolution. In the limit when h tends to zero, the smoothing function W becomes a Dirac delta function, and the smoothed representation $A_{s}(\mathbf{r})$ tends to A(r).

In SPH, Eq. (1) is then approximated as a sum over all neighbouring particles. For instance, the mass density at the position of particle i, say $\mathbf r _{i}$ with $i=1,{\ldots }, N$, where N is the total number of neighbours, is given by

$$\begin{aligned} \rho _i =\sum _j {m_j W(\mathbf{r}_i -\mathbf{r}_j ,h)} , \end{aligned}$$

(2)

where the subscripts denote particle labels, $m_{j}$ is the mass of neighbouring particle j, and $W(\mathbf r _{i}-\mathbf r _{j}, { h}$) is a spherically symmetric kernel function here given by the cubic B-spline kernel of Monaghan (1985).

The position and velocity of particle i are given by the SPH representations

$$\begin{aligned} \frac{d\mathbf{r}_i }{dt}&=\mathbf{v}_i , \\ \frac{d\mathbf{v}_i^\alpha }{dt}&=\sum \limits _{j=1}^N {m_j \left( {\frac{\sigma _i^{\alpha \beta } }{\rho _i^2 }+\frac{\sigma _j^{\alpha \beta } }{\rho _j^2 }} \right) }\!\cdot \nabla W_{ij}^h , \end{aligned}$$

(3)

where $\sigma$ is the total stress tensor. Here the Greek indices are employed to denote the components of the vector and tensor fields.

Water drops are simulated using a general Mie-Grüneisen equation of state with different analytic forms for the states of compression ($\rho /\rho _{0}-1) > 0$ and tension ($\rho /\rho _{0}-1) < 0$ (Acevedo-Malavé and García-Sucre 2011a).

3 Coalescence, Fragmentation, and Flocculation of Drops

We simulate the impact of three unequal-sized water drops on a bigger drop. We consider spherical drops of diameters $5$, $8$, $12$, and $20\,\upmu \mathrm{m}$ represented by 4,456, 10,728, 15,504, and 34,040 SPH particles, respectively. The impacting drops have all collision velocities that are directed towards the centre of the coordinate system.

For a collision velocity of 15.0 mm/ms, Fig. 1 shows that at ${ t}=8.7\times 10^{-5}\,\mathrm{{ms}}$ a flat circular section appears after the drops enter in contact with one another, which then increases in diameter as coalescence proceeds. At ${ t}=1.5\times 10^{-4}\,\mathrm{{ms}}$, the fluid of the smaller drops begins to penetrate into the bigger drop. By ${ t}=3.5\times 10^{-4}\,\mathrm{{ms}}$ the smallest drop has already coalesced with the bigger one, while the other two drops are already in the process of coalescing. Although we have terminated the calculation at this time, the evolution will eventually end with the formation of a big drop oscillating about a spherical shape (permanent coalescence). Figure 2 shows the velocity vector field inside the colliding drops as well as in the region of contact between them at ${ t}=1.5\times 10^{-4}\,\mathrm{{ms}}$. Inside the drops, the fluid velocity tends to a value close to the impact velocity of 15.0 mm/ms, while in their areas of contact maximum velocities of about 30.0 mm/ms are observed.

For impact velocities as high as 30.00 mm/ms, the evolution is similar except that an outwardly directed flow develops in the contact region perpendicular to the direction of incidence of the drops, which may eventually condense into satellite droplets (see Fig. 3). While some of this liquid may return to the coalescing system, some other may condense into independent small droplets; the final process leading to permanent coalescence into a big drop accompanied by fragmentation into much smaller droplets. In Fig. 4 we show the velocity vector field inside the drops at $8.7\times 10^{-5}\,\text {ms}$. Maximum velocities are 25 mm/ms in the bigger drop and 32 mm/ms in the smaller ones, while in the zones of contact between them the fluid reaches velocities as high as 40 mm/ms.

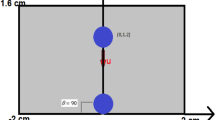
When the impact velocity is lowered to $\mathrm{V}_{\text {col}}=0.5\,\text {mm/ms}$, the smaller drops do not coalesce but rather remain attached to the bigger one as shown in Fig. 5. In this case, the drops interact only through their deformed surfaces of contact, forming a clustering (drop flocculation). The stretching of the drop surfaces at contact is due to the fact that the surface tension forces prevail and the inertial forces are too low to induce permanent coalescence. Figure 6 shows the velocity vector field at ${ t}=7.2\times 10^{-3}\,\mathrm{{ms}}$ during the flocculation process. The maximum fluid velocity inside the drops is now around 0.47 mm/ms for the bigger one and 0.3 mm/ms for the smaller drops. In the zones of drop contact the maximum velocity is about 0.12 mm/ms.

4 Conclusions

In this chapter, we have presented numerical simulations of the coalescence collision of unequal-sized multiple drops in three-space dimensions, using the method of Smoothed Particle Hydrodynamics (SPH). For impact velocities in the range of 0.5 $\le {\text {V}}_{\text {col}} \le 30\,\text {mm/ms}$, the simulations predict three different outcomes: (a) the formation of a clustering of drops (flocculation), where the smaller drops do not undergo coalescence but remain attached to the bigger one, for low impact velocities; (b) permanent coalescence for moderate impact velocities; and (c) permanent coalescence accompanied by fragmentation into much smaller satellite droplets, as a consequence of an outflow of liquid along the plane of contact between the drops, for higher impact velocities. Future work in this direction will explore the ability of the present SPH scheme to follow the collision process for much higher impact velocities ($\le$30 mm/ms) in order to study shattering separation for colliding drops of similar size and penetration of small drops into bigger ones.