Experimental Investigation of Thermal Diffusion in Binary Fluid Mixtures

Abstract

The mass transport of chemical species in response to a temperature gradient, referred to as the Soret effect or thermal diffusion, leads under certain conditions to a separation of the chemical constituents. The Soret coefficient is the ratio of the thermodiffusion coefficient to the molecular diffusion coefficient. This effect along with molecular diffusion occurs in many natural phenomena and engineering systems. One early application of this effect was the separation of isotopes. Understanding the Soret effect is also important for exploring the mechanics of crude oil extraction and its reservoir characterization, as well as in the research of the global circulation of see water. It has also been used for polymer characterization by thermal field flow fractionation. Moreover, recent studies on the Soret effect of bio-systems, like protein and DNA solutions, indicate that it might help revealing the mechanisms behind the mysterious phenomenon of life. Many experimental techniques have been developed for investigation of the Soret effect: thermogravitational columns, thermal lens, diffusion cells, thermal diffusion forced Rayleigh scattering, thermal field flow fractionation, and microfluidic fluorescence. In this chapter, we focus on the investigation of thermal diffusion behaviour in simple liquid mixtures by a thermal lens method. The big advantage of the thermal lens method is that it is fast, simple, and the experimental set-up is much cheaper compared to other methods. In particular, a calibrated two-beam mode-mismatched thermal lens experiment is used for determining the Soret coefficient for isopropanol/water and ethanol/water mixtures.The fitting curves show a very good agreement between the theoretical model and the experimental data. The experimental results have also shown good agreement with available thermodiffusion coefficient data.

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

1 Introduction

Thermal diffusion, known also as the Ludwig–Soret effect, plays an important role in our understanding of the properties of liquid mixtures (Sitzber 1856; Soret 1879). It characterizes the flux of matter in response to a temperature gradient, which leads to the formation of a concentration gradient (Bierlein 1955). This stationary concentration gradient is given by

$$\begin{aligned} \nabla c=-S_{T}c_{0}(1-c_{0})\nabla T, \end{aligned}$$

(1)

where $S_{T}=D_{T}/D$ is the Soret coefficient, $D$ the mass-diffusion coefficient, $D_{T}$ the thermal diffusion coefficient, $T$ the temperature, $c$ the molar fraction of component 1 (the heaviest component), and $c_{0}$ its equilibrium value (Tyrell 1961).

The thermal lens method (TL) is a powerful method that can be used to study the Soret effect in transparent liquid mixtures. The TL measures the amount of heat deposited in a medium after the absorption of light. Immediately after the absorption of photons, the spatial heat distribution resembles the intensity distribution of the beam spot. Later on, the thermal diffusion spreads the heat over distances more than $1$ order of magnitude larger than the excitation beam spot radius. Since the refractive index depends on temperature, a spatial distribution of the refractive index of a similar extent is generated in the absorbing medium. In addition to the temperature-dependent refractive index gradient, the Soret effect can produce refractive index changes and influence the total signal (Giglio and Vendramini 1974). For CW excitation the generation of a stationary TL can take milliseconds to several seconds, depending on the beam spot radius and the thermal diffusivity of the sample. The TL alters the propagation of the probe beam through the medium by generating a phase shift on the beam wavefronts. Since the first report on the thermal lens effect, the sensitivity of the technique has been improved by changing the experimental configuration. Early experimental arrangements used a single-beam configuration, which employed a laser beam to excite the TL and probe it (Whinnery 1974). The use of a second probe beam for testing the TL has improved the versatility and sensitivity of the technique (Long et al. 1976; Shen et al. 1992; Marcano et al. 2006; Cabrera et al. 2009a). The dual-beam configuration provides the possibility to use signal processing devices, e.g. lock-in amplifiers, to improve the signal-to-noise ratio and hence the sensitivity of the TL measurement. In addition, detection optics and detectors can be optimized for a single, convenient probe laser wavelength rather than requiring detection in what may be a more difficult spectral region, which is a convenient choice for generating continuous scanning TL spectra (Shen et al. 1992).

An advantage of the thermal lens method compared to the diffusion cell is the short duration of a typical experiment (short equilibration times) due to small distances on the order of the focal beam width. Furthermore, in thermal lens experiments typical temperature changes are on the order of $10^{-2}\,{-}\,10^{-5}\,{^{\circ }}$C (Gordon et al. 1965; Whinnery 1974). This allows to work with extremely small temperature and concentration gradients, so that the addition of a dye can be avoided by using the natural absorption of the molecules. Such advantages make the Soret coefficient independent of the effects of convection. In the same way, the sensitivity to convection may be neglected for fast diffusing systems such as, for example, water/organic solvent mixtures.

In this work, a calibrated two-beam mode-mismatched thermal lens experiment, where the pump beam is tightly focused and the probe beam is collimated, was used for determining the Soret coefficient of alcohol-water systems. This particular set-up provides the maximum possible response in terms of the amplitude of the signal in a CW photothermal experiment (Marcano et al. 2006). In addition, the alignment procedure, the experiment itself as well as its calibration, and the interpretation of the experimental results are simpler than working with the mode-matched configuration (Long et al. 1976).

2 Theoretical Model

In the mode-mismatched dual-beam thermal lens experiment when an infinite medium is illuminated, at time $t=0$ along the $z$-axis, with a light beam of Gaussian intensity $I(r,z)=[2P_{e}/\ \pi \omega _{e}^{2}(z)]\exp [-2r^{2}/\omega _{e}^{2}(z)]$, in the limit of small absorption values, the temperature distribution is given by Shen et al. (1992)

$$\begin{aligned} \varDelta T(r,z,t)=\frac{2P_{e}\alpha }{\pi \rho C_{p}\omega _{e}^{2}}\int \limits _{0}^{t}\frac{t_{c}}{t_{c}+2t'} \exp \left[ -\frac{2t_{c}r^{2}}{\omega _{e}^{2}(t_{c}+2t')} \right] \mathrm{{d}}t', \end{aligned}$$

(2)

where $P_{e}$ is the excitation power, and $\alpha$, $\rho$, and $C_{p}$ are, respectively, the absorption coefficient, the density, and the specific heat of the medium. The quantity $\omega _{e}(z)=\omega _{0e}[1+(z-a_{e})^{2}/z^{2}_{e}]^{1/2}$ is the excitation beam radius at the sample cell, where $a_{e}$, $\omega _{0e}$, $z_{e}=\pi \omega _{0e}^{2}/\lambda _{e}$, and $\lambda _{e}$ are the waist position, the radius at the waist, the Rayleigh parameter, and the excitation wavelength, respectively. The coordinate $z$ is the sample position, $r$ is the coordinate radius, $t_{c}(z)=\omega _{e}^{2}(z)/4D_{{ th}}$ is the characteristic thermal time constant, with $D_{{ th}}=k/\rho C_{p}$ and $k$ being the thermal diffusivity and thermal conductivity, respectively.

If the refractive index $n$ of the liquid mixture satisfies the condition $\varDelta n/n<<1$ (Gordon et al. 1965), its change with temperature and concentration is given by (Bierlein 1955)

$$\begin{aligned} \varDelta n(r,z,t)=\frac{\partial n}{\partial T}\varDelta T(r,z,t)+\frac{\partial n}{\partial c}\varDelta c(r,z,t), \end{aligned}$$

(3)

while the concentration change is (Bierlein 1955)

$$\begin{aligned} \varDelta c(r,z,t)=-S_{T}c_{0}(1-c_{0})\varDelta T(r,z,t)\varGamma (z,t), \end{aligned}$$

(4)

with

$$\begin{aligned} \varGamma (z,t)=1-\sum \limits _{i=1}^{\infty }\frac{4}{(2i-1)\pi }\sin \left[ \frac{(2i-1)\pi }{2}\right] \exp \left[ -(2i-1)^{2}\frac{t}{t_{D}(z)}\right] , \end{aligned}$$

(5)

where $t_{D}(z)=\omega _{e}^{2}(z)/4D$ is the mass-diffusion time (Arnaud and Georges 2001).

The expansion in Eq. (5) converges rapidly. In order to obtain an accuracy better than $1$ % it is sufficient to retain terms up to $i=4$ in the summation. When $t>>t_{D}$, the exponential term vanishes and $\varGamma =1$, and so Eq. (4) reduces to Eq. (1).

The change of the refractive index acts as an optical element producing a phase shift $\varPhi$ on the wavefronts of the probe beam. Inserting Eq. (4) into Eq. (3) and then using Eq. (3), we obtain for the phase shift (Marcano et al. 2002; Cabrera et al. 2009a)

$$\begin{aligned} \varPhi (r,z,t)&=\frac{2\pi }{\lambda _{p}}l[\varDelta n(r,z,t)-\varDelta n(0,z,t)]\nonumber \\&=\frac{2\pi }{\lambda _{p}}l \left[ \frac{\partial n}{\partial T}-\frac{\partial n}{\partial c}S_{T}c_{0}(1-c_{0})\Gamma (z,t)\right] \nonumber \\&\quad \times [\varDelta T(r,z,t)-\varDelta T(0,z,t)], \end{aligned}$$

(6)

where $l$ is the sample cell length and $\lambda _{p}$ is the wavelength of the probe field. Substituting Eq.( 2) into Eq.( 6), $\varPhi$ can be written as (Marcano et al. 2002; Cabrera et al. 2009a)

$$\begin{aligned} \varPhi (g,z,t)&=\frac{\phi _{s}\varGamma (z,t)- \phi _{{th}}}{2}\nonumber \\&\quad \times \int \limits _{\left( 1+2t'/t_{c}\right) ^{-1}}^{1} \frac{[1-\exp (-2m(z)g\tau )]}{\tau }\mathrm{{d}}\tau , \end{aligned}$$

(7)

where $\phi _{s}=(\partial n/\partial c)[P_{e}\alpha lS_{T}c_{0}(1-c_{0})/k\lambda _{p}]$ is the induced concentration phase shift amplitude and $\phi _{\text {th}}=(\partial n/\partial T)(P_{e}\alpha l/k\lambda _{p})$ is the induced thermal lens phase shift amplitude. In the above equation, the ratio $m(z)=[\omega _{p}(z)/\omega _{e}(z)]^{2}$ accounts for the level of mode-matching between the beams, $g=r/\omega _{p}(z)$ is a dimensionless parameter, and $\omega _{p}(z)=\omega _{0p}[1+(z-a_{e})^{2}/z^{2}_{p}]^{1/2}$ is the probe beam radius at the sample cell, with $a_{p}$, $\omega _{0p}$, and $z_{p}=\pi \omega _{0p}^{2}/\lambda _{p}$ being the waist position, the radius at the waist, and the Rayleigh parameter.

The phase shift is added to the wavefront of the propagating probe light. At the exit of the sample the amplitude of the probe light is (Marcano et al. 2002)

$$\begin{aligned} E_{p}(r,z,t)=\frac{\sqrt{2P_{p}/\pi }}{\omega _{p}(z)}\exp \left[ -\frac{r^{2}}{\omega _{p}(z)}- ik_{p}z-i\frac{k_{p}r^{2}}{2R(z)}+i\arctan \left( \frac{z-a_{p}}{z_{p}}-i\varPhi \right) \right] \!, \end{aligned}$$

(8)

where $P_{p}$ is the total power of the probe light beam, $k_{p}=2\pi /\lambda _{p}$ is the probe light wave number, and $R(z)=[(z-a_{p})^{2}+z_{p}^{2}]/z$ is the radius of curvature of the probe beam at the sample position $z$.

Behind the sample cell the probe beam propagates freely up to the position of the aperture. The next step is to calculate the probe beam amplitude at the position of the detector. The Fresnel diffraction approximation provides the solution of this problem. It is given by the convolution of the probe field amplitude $E_{p}(r,z,t)$ at the exit of the sample with the impulse response of free space propagation (Marcano et al. 2002).

Finally, the time-dependent total signal can be calculated using the definition (Shen et al. 1992):

$$\begin{aligned} S(z,t)=\frac{I(z,t)-I_{0}}{I_{0}}, \end{aligned}$$

(9)

where $I(z,t)=2\pi \int _{a}|E_{p}(r,z,t)|^{2}r{ {d}}r$ is the transmission of the aperture in the presence of the excitation beam, $I_{0}$ is its transmittance in the absence of the excitation beam, and $a$ represents the aperture surface. If we consider a small phase shift ($\varPhi <<1$) and aperture dimensions much smaller than the probe beam spot, a simple solution can be obtained by means of Eq. (8) and the Fresnel diffraction approximation. Considering the Soret effect in liquid mixtures, the time-dependent total signal which is the sum of the pure thermal lens plus the Soret concentration lens can be expressed as follows (Marcano et al. 2002; Cabrera et al. 2009a):

$$\begin{aligned} S_{{total}}(z,t)=S_{th}-S_{s}=\frac{P_{e}\alpha lK(z,t)}{k\lambda _{p}}\left[ \frac{\partial n}{\partial T}- \frac{\partial n}{\partial c}S_{T}c_{0}(1-c_{0})\varGamma (z,t)\right] \!, \end{aligned}$$

(10)

with

$$\begin{aligned} K(z,t)=\arctan \left\{ \frac{4m\nu t/t_{c}}{\nu ^{2}+ [1+2m]^{2}+[1+2m+\nu ^{2}]2t/t_{c}}\right\} \!, \end{aligned}$$

(11)

$$\begin{aligned} \varGamma (z,t)&=1-\sum \limits _{i=1}^{\infty }\frac{4}{(2i-1)\pi }\sin \left[ \frac{(2i-1)\pi }{2}\right] \nonumber \\&\quad \times \exp \left[ -(2i-1)^{2}\frac{t}{t_{D}(z)}\right] \!, \end{aligned}$$

(12)

where $\nu (z)=(z-a_{p})/z_{p}+(z_{p}/L-z)[1+(z-a_{p})^{2}/z_{p}^{2}]$ is the geometrical parameter of the probe beam and $L$ denotes the position of the plane detector.

The mode-mismatched scheme optimizes the value of the stationary total signal when $K(z,t)$ in Eq. (10) reaches its maximum value of $\pi /2$. In the stationary situation ($t\rightarrow \infty$), this value is reached at $z=0$ for $z_{p}>>L>>z_{e}$. This corresponds to a situation with a collimated probe beam and a tightly focused pump beam. Under these conditions $K(z,t)=\pi /2$ , $\varGamma =1$, and Eq. (10) can be re-written as (Marcano et al. 2006; Cabrera et al. 2009a)

$$\begin{aligned} S_{{{ total}}\infty }=S_{{ th}}-S_{s}=\phi _{{ th}}\frac{\pi }{2}-\phi _{s}\frac{\pi }{2}= \frac{P_{e}\alpha l\pi }{k\lambda _{p}2}\left[ \frac{\partial n}{\partial T}- \frac{\partial n}{\partial c}S_{T}c_{0}(1-c_{0})\right] . \end{aligned}$$

(13)

Equation (13) provides a relation between the total signal $S_{{{ total}}\infty }$ and the Soret coefficient $S_{T}$. Measuring the total signal and calculating the thermal lens signal, the Soret signal can be obtained, which is then used to determine the Soret coefficient whenever the rest of the parameters are known. However, the ratio of the Soret signal and the pure thermal lens signal provides the more compact expression (Polyakov and Wiegand 2009; Cabrera et al. 2013):

$$\begin{aligned} S_{T}=\frac{\frac{\partial n}{\partial T}}{\frac{\partial n}{\partial c}c_{0}(1-c_{0})}\frac{S_{s}}{S_{{ th}}}. \end{aligned}$$

(14)

In this relation there are three unknown parameters: the Soret coefficient $S_{T}$, the thermal lens signal $S_{th}$, and the Soret signal $S_{s}$. With the use of Eq. (14) we do not need to determine the absorption coefficient, and so avoid the addition of dye to increase the absoption. This particular property reduces the uncertainty in the determination of the Soret coefficient.

We can obtain the Soret signal $S_{s}$ as the difference between the final steady-state total signal $S_{{{ total}}\infty }$ and the value of the pure thermal lens signal $S_{{ th}}$, which is obtained by extrapolating the fit of the thermal lens contribution from Eq. (10) in the $0{\text {--}}500$ ms range. Finally, the Soret coefficient $S_{T}$ is calculated using Eq. (14).

3 Experimental Method

The dual-beam thermal lens experimental set-up (see Fig. 1) has recently been used for the measurement of the Soret effect (Cabrera et al. 2009a, b, 2013). The system is composed of two blocks as follows:

• 1. Probe beam and recording block. The He–Ne laser ($\lambda _{p}=632.8\,\mathrm{nm }$, $P_{p}=10\,\mathrm{mW }$, Spectra Physics) generates the probe beam. This beam passes through a 1 cm $L_{1}$ and 30 cm $L_{2}$ focal-length lenses, resulting in a $6\,\mathrm{mm }$ width near-collimated probe beam. This beam is reflected by mirror $E_{1}$, passes through the dichroic beam combiner DivD, the sample M (contained in a 1 cm quartz cuvette), and the interference filter $F_{1}$ (central wavelength $\lambda =632.8\,\mathrm{nm }$, Thorlabs). The dichroic mirror $E_{2}$ then reflects the beam towards the 0.3 mm pinhole A and the photodetector D (model DET 110/M, Thorlabs). The output signal of the photodetector is transformed by the current pre-amplifier Amp (model SR570, Stanford Research Systems) and introduced into the digital oscilloscope Osc (model TDS 3052, Tektronix), where the signal is digitized, saved, and processed statistically. The radiant flux of the probe beam at the sample surface is 0.2 mW.

• 2. Excitation beam block. The second harmonic of a diode pumped neodymium yttrium aluminum garnet (Nd:Yag) CW laser (model GSF32–200,$\lambda _{e}=532.8$ nm, $P_{e}=200$ mW, Intelite) delivers the excitation beam through the shutter Sh (model 846, Newport Corporation), the beam splitter Div, and the 180  mm focal length lens $L_{3}$ to the beam combiner DivD, which reflects it to the sample M. The excitation beam passes from the left to the right through the sample cell. The interference filter F and the dichroic mirror $E_{2}$ block the excitation beam preventing it from reaching the pinhole A and the photodetector. The beam reflected from the beam splitter Div is sensed by the photodetector Ref (model DET 110/M, Thorlabs), which transforms the incident radiant flux into a synchronization signal for the oscilloscope.

Fig. 1

Experimental set-up. Lenses $L_{1}$ and $L_{2}$: form the beam expander, $E_{1}$: mirror, DivD: dichroic beam combiner, M: sample, F: interference filter, $E_{2}$: dichroic mirror, A: pinhole, D: photodetector, Amp: current pre-amplifier, Osc: digital oscilloscope, Sh: shutter, Div: beam splitter, $L_{3}$: lens, and Ref: reference photodetector

Measurements were taken according to the following procedure: the shutter Sh modulates the beam with a period of $10$ s, and for each sample the signal was obtained from the average of $128$ recordings at the digital oscilloscope. In order to measure the value of the final steady-state total signal $S_{{{ total}}\infty }$, we have recorded the relative change of the transmission of the probe light through the aperture according to the definition given by Eq. (9), which allowed us to determine $S_{{ th}}$, $S_{s}$, and $S_{T}$.

The water/isopropanol and water/ethanol mixtures were prepared using distilled and de-ionized water (with a purity of better than 99 %) and Fisher Scientific chemical organic components (with a purity of 99.8 %).

4 Results and Discussion

The evolution of the total experimental signal with time is shown in Fig. 2 for a water/isopropanol mixture with an initial mass fraction of isopropanol $c_{0}=0.5$ (at $298$  K). Using Eq. (10), the best fit to the experimental data gives $S_{T}=-5.2\times 10^{-3}$ $K^{-1}$, when the fitting parameters are: $\lambda _{e}=532.8\,\mathrm{nm }$, $\lambda _{p}=632.8$ $\mathrm{nm }$, $z_{p}=100,000$ $\mathrm{cm }$, $z_{e}=0.0001\,\mathrm{cm }$, $a_{e}=0$, $a_{p}=0$, $L=50$  $\mathrm{cm }$, $m=10,000$, $\partial n/\partial T=-3.474\times 10^{-4}$ $K^{-1}$ (Mialdun et al. 2012), $P_{e}=73$ $mW$, $\alpha =2\times 10^{-4}$ $cm^{-1}$, $l=1$ $cm$, $k=3\times 10^{-3}$  $Wcm^{-1}K^{-1}$, $\partial n/\partial c=-0.0364$ (Mialdun et al. 2012), $c_{0}=0.5$, and $t_{D}=1$ $\mathrm{s }$. If we cut the fit at $t_{c}=500$ ms, only the pure thermal lens signal takes place (first term of Eq. (10), represented by the red line).

Fig. 2

Time evolution of the total experimental signal ($S_{{{ total}}\infty }=-0,041$) for a water/isopropanol mixture with $c_{0}=0.5$ at $T=298$ $\mathrm{K }$. The red line is the best fit of the first term of Eq. (10) to the experimental data and represents the pure thermal lens signal. The inset box shows the build-up of the initial thermal lens effect in a 2 s period with $t_{c}=500$ ms

As we may see from this figure, the signal first shows a rapid reduction due to the pure thermal lens effect, followed by a further, much slower, decrease due to the build-up of the Soret concentration gradient. Both processes can be easily separated because the Soret component builds up with a time constant which is much greater ($t_{d}=1$ s) than the characteristic time constant of the thermal lens ($t_{c}=500$ ms) (Arnaud and Georges 2001; Cabrera et al. 2009a). The separation of the time scales allows for an analysis of the temporal build-up of the pure thermal lens, which is shown in expanded scale in the inset box of Fig. 2. The fit was limited to a short period, typically $500$ ms, within which mass diffusion is inoperative and the signal is only governed by the temperature-dependent refractive index gradient. The fit allowed the determination of the transient steady-state thermal lens signal ($S_{\text {th}}=-0.036$), from which the Soret signal ($S_{s}=0.005$) was taken as the difference between the final steady-state total signal ($S_{{{ total}}\infty }=-0,041$) and the steady-state pure thermal lens signal extrapolated from the fit using only the first term of Eq. (10). Then we have determined the Soret coefficient ($S_{T}=-5.34\times 10^{-3}$ $K^{-1}$) by means of Eq. (14) with $c_{0}=0.5$, $\partial n/\partial T=-3.474\times 10^{-4}$ $K^{-1}$ (Mialdun et al. 2012), and $\partial n/\partial c=-0.0364$ (Mialdun et al. 2012). The Soret coefficient obtained from the fitting procedure ($S_{T}=-5.2\times 10^{-3}$ $K^{-1}$) does coincide with the calculated one using Eq.( 14) ($S_{T}=-5.34\times 10^{-3}$ $K^{-1}$). This result demonstrates that the model predictions are in good agreement with the experimental data.

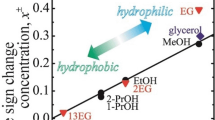
We have applied a similar procedure to determine the Soret coefficients for different concentrations of water/isopropanol mixtures. The results are summarized in Fig. 3  (Cabrera et al. 2013). For comparison, the data for the Soret coefficients from recent measurements by Mialdun et al. (2012) and Mialdun and Shetsova (2008), using three different instrumental techniques, and from early measurements by Poty et al. (1974), using flowing cell methods, are also displayed in Fig. 3. These results show a reasonably good agreement with ours in the region $0.2<c_{0}<0.8$, except for the Soret coefficient reported by Poty et al. (1974) for $c_{0} = 0.7$, which being too high, deviates significantly from all other data. In the region with low water content ($c_{0}<0.2$), our results also disagree with those reported by Poty et al. (1974). In addition, at low water concentrations the contrast factors are very low, which means that the concentration variations become invisible to the optical techniques and so the measurements of the transport properties are subject to large errors. The results of the measurements in this region are not shown in Fig. 3 because they were considered to be unreliable. Note that the Soret coefficient changes sign at low and high isopropanol concentrations. In Fig. 3 we also compare our experimental results with the predictions of the viscous energy model developed by Abbasi et al. (2009). A reasonably good agreement is also observed.

Fig. 3

Soret coefficient of water/isopropanol mixtures as a function of the mass fraction of water (black circles: present work). The open blue squares represent the experimental data reported by Mialdun and Shetsova (2008), while open red circles correspond to data from Poty et al. (1974). The green squares are the predicted values of the viscous energy model developed by Abbasi et al. (2009). The continuous orange line is a spline fit to all available data (Mialdun et al. 2012)

We have also applied our technique to mixtures of ethanol and water at $298$ $\mathrm{K }$. The solid red circles in Fig. 4 show the measured Soret coefficients $S_{T}$ as a function of the mass fraction of ethanol. Positive Soret coefficients are observed for low ethanol contents. By increasing the ethanol content, the Soret coefficient decays and changes sign at $c\sim 0.3$. In a mixture with high ethanol content, $S_{T}$ is negative (because the ethanol molecules migrate to the hot side), whereas at low ethanol content, $S_{T}$ is positive (in this case, the ethanol molecules migrate to the cold side). For comparison, Fig. 4 also depicts the experimental results reported by Kolodner et al. (1988), Zhang et al. (1996), and Kita et al. (2004). In addition, we also compare the results with the predictions of Abbasi et al. (2009). We see that the agreement between these three data sets, the viscous energy model, and our results is excellent.

Fig. 4

Soret coefficient as a function of the mass fraction of ethanol. Solid red circles refer to the experimental data measured in the present work. Cross black circles represent previous results from Kolodner et al. (1988), green solid circles from Zhang et al. (1996), and open blue squares from Kita et al. (2004). The continuous black line draws the predictions of the viscous energy model developed by Abbasi et al. (2009)

We notice that for both mixtures the change of sign in the Soret coefficient occurred at an alcohol mass fraction of $c\sim 0.3$. Regarding this fact, a model for the calculation of thermodiffusion in associating mixtures was proposed. In this model a new approach for calculating the viscous energy and the ratio of the evaporation energy to the viscous energy was developed (Abbasi et al. 2009). Thus, the variation of the viscous energy of the organic component is considered to control the sign change in the Soret coefficient. In these two mixtures, the viscous energy of the organic component decreases sharply with its concentration, which leads to a sign change in the Soret coefficient. It then increases gradually with decreasing water concentration in the systems. For the isopropanol-water mixture, the isopropanol viscous energy increases to the point where a second change of sign occurs. However, the viscous energy of ethanol does not increase enough to cause a second change of sign in the thermodiffusion factor (Abbasi et al. 2009).

5 Conclusions

We have used an optimized thermal lens experiment that allowed the precise determination of the values of the Soret coefficient for isopropanol/water and ethanol/water mixtures. Our experimental results were seen to compare well with existing data in the literature. We observed that the Soret coefficient of alcohol/water mixtures depends strongly on the concentration, with a change of sign at alcohol mass fractions of $c\sim 0.3$. In addition, for the isopropanol/water mixture, the isopropanol viscous energy increased to the point where a second change of sign occurred for the Soret coefficient. These results suggest a relation with the variation of the activation energy of the organic component. While there is not a unique technique for measuring the Soret coefficient, the results obtained here shows that a calibrated two-beam mode-mismatched thermal lens experiment represents an additional independent method, which provides new reliable benchmark data that agree quite well with previously reported measurements in the literature.