Keywords

1 Background

Complex systems have undergone intense, interdisciplinary study in recent decades, with network science [3, 28] having emerged as a viable framework for understanding complexity in domains ranging from economics and finance [15, 16, 22, 23, 26], to ‘wicked’ social problems such as human trafficking and terrorism [21, 24, 25, 40]. Communication networks, as well as many other natural and social networks that are modeled as complex systems, have the scale-free topology in common. The preferential attachment model [8, 44] has been suggested as a candidate network evolution or ‘growth’ model to yield such topologies in complex networks by formalizing the intuition that highly connected nodes increase their connectivity faster than their less connected peers. The degree distribution of such networks exhibits power-law scaling [20].

While early studies in network science tended to be limited to lower-order structures like dyadic links or edges [14, 32, 34, 37] (and later, triangles), a recent and growing body of research has revealed that deep insights can be gained from the systematic study of non-simple networks, multi-layer networks [33] and ‘higher-order’ structures [46] in simple networks [1, 5, 13, 19, 43].

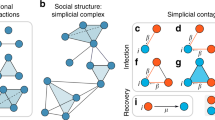
One such higher-order structure that continues to undergo study is a simplicial complex (often just referred to as a ‘complex’) [4, 17, 42]. The study of simplicial complexes first took root in mathematics (especially, algebraic topology) [6, 10, 27, 30, 31], but in the last several years, have found practical applications in network science (as discussed in Related Work). Figure 1 provides a practical example of two such simplicial complexes that have been studied in the literature, especially in theoretical biology and protein interaction networks. Due to space limitations, we do not provide a full formal definition; a good reference is [9], who detailed some of their properties and even proposed centrality measures due to their importance. An S-complexFootnote 1 is defined by a ‘central’ edge A-B, with one or more triangles sharing that edge. A T-complex is similar but the central unit is a triangle (A-B-C). Furthermore, non-central (or peripheral) triangles in a T-complex should not also participate in quads with the central triangle i.e., given central triangle A-B-C and peripheral triangle A-B-V3, there should be no link between V3 and C in a valid T-complex. As we detail subsequently, the adjacency factor of either an S*- or T*-complex is the number of triangles flanking the central structure (an edge or triangle respectively).

Fig. 1.
figure 1

Illustration of an S* simplicial complex and T* simplicial complex, defined in the text.

Full size image

Simplicial complexes have been widely used to analyze aspects of diverse multilayer systems, including social relation [45], social contagion [35], protein interaction [39], linguistic categorization [12], and transportation [29]. New measurements, such as simplicial degree [39], simplicial degree based centralities [9, 38], and random walks [36] have all been proposed to not only measure the relevance of a simplicial community and the quality of higher-order connections, but also the dynamical properties of simplicial networks.

However, to the best of our knowledge, the distributional properties of such complexes, especially in the context of communication networks, have not been studied so far. A methodology for conducting such studies has also been lacking. Therefore, given the growing recognition that these two structures play an important role in real networks, and with this brief background in place, we propose to investigate the following research questions (RQs):

RQ1: In real-world communication networks, what are the respective distributions of S*- and T*-complexes? Can good functional fits be found for these distributions?

RQ2: Can (and to what extent) the scale-free network growth model (with triad formation) accurately capture these distributions? Or are additional parameters and steps (beyond triad formation) needed to model these higher-order structural properties in real-world networks?

2 Methodology

Since our primary goal in this paper is to understand whether (and to what extent) the scale-free network growth (with triad formation) model can accurately and empirically capture the two simplicial complexes described in the introduction, we first briefly recap the details of the growth model below. Full details are provided in [18].

2.1 Scale-Free Network Growth with Triad Formation

Networks with the power-law degree distribution have been classically modeled by the scale-free network model of Barabási and Albert (BA) [2]. In the original BA model, the initial condition is a network with \(n_0\) nodes. In each growth timestep, an incoming node v is connected using m edges to existing nodes in the network. The connections are determined using preferential attachment (PA), wherein an edge between v and another node w in the network is established with probability proportional to the degree of w.

The growth model informally described above is known to generate a network with the power-law degree distribution; however, other work has found that such networks lack triadic properties (including observed clustering coefficient) in real networks. In order to incorporate such higher-order properties, the growth step in BA model was extended by [18] to include a triad formation (TF) step. Specifically, given that an edge between nodes v and w was attached using preferential attachment, an edge is also established from v to a random neighbor of w with some probability. If all neighbors of w are connected to v, this step does not apply.

In summary, when a ‘new’ node v comes in, a PA step will first be performed, and then a TF step will be performed with probability \(P_t\) (in other words, the probability of PA without TF is \(1-P_t\)). These two steps are performed repeatedly per incoming node until m edges are added to the network. \(P_t\) is the control parameter in the model. It has been shown to have a linear relationship with the network’s average (over all nodes) clustering coefficientFootnote 2.

Table 1. Details on five real communication networks (including average clustering coefficient) used in this paper.
Full size table

2.2 Adjacency Factor

To understand the distributional properties of the S*- and T*- complexes in the generated network versus real communication networks, we use the notion of the adjacency factor. From the earlier definition, we know that an S*-complex is defined by a ‘central’ edge (A-B in Fig. 1 (a)) that is adjacent to a certain number of triangles. Given an edge in the network, therefore, we denote the adjacency factor (with respect to S*-complexes) as the (maximal) number of triangles adjacent to that edge. For example, the adjacency factor of edge A-B in Fig. 1 (a) would be 3, not 1 or 2. While we record adjacency factors of 0 alsoFootnote 3 to obtain a continuous distribution, only cases where adjacency factor is greater than 0 constitute valid S*-complexes.

Similarly, the adjacency factor (with respect to T*-complexes) applies to triangles in the network. For every triangle A-B-C (see Fig. 1 (b)), the adjacency factor is the (maximal) number of triangles adjacent to itFootnote 4 in the T*-complex configuration. If no (non-quad) triangles are adjacent to any of the edges of the central A-B-C triangle, then the adjacency factor is 0, meaning that the triangle does not technically participate in a T*-complex.

Hence, depending on whether we are studying and comparing S*- or T*-complex distributions, an adjacency factor can be computed for each edge and each triangle (respectively) in the network. We compute a frequency distribution over these adjacency factors to better contrast these higher-order structures in the grown versus the actual networks from a distributional standpoint.

3 Experiments

Fig. 2.
figure 2

Frequency distribution of adjacency factors (described in the text) of S*-complexes in the real Email-EU, Email-DNC, and University of Kiel email networks (distributions for the other two datasets are qualitatively similar) and the generated networks with the PA-TF generated networks sharing the same number of nodes, edges, and average clustering coefficient (Table 1) as their real counterparts. In all plots, the actual adjacency-factors distribution is always shown as a solid line and the corresponding estimated function with best-fit parameters (Eqs. 1) as a dashed line. Both figures are on a log-log (with base 10) scale.

Full size image
Fig. 3.
figure 3

Frequency distribution of adjacency factors (described in the text) of T*-complexes in the real Email-EU, Email-DNC, and University of Kiel email networks (distributions for the other two datasets are qualitatively similar). The actual adjacency-factors distribution is shown as a solid line, and the corresponding estimated function with best-fit parameters (Eqs. 2) as a dashed line.

Full size image

We use five publicly available communication networks in our experiments, including Enron email communication network (Email-EnronFootnote 5), 2016 Democratic National Committee email leak network (Email-DNCFootnote 6), a European research institution email data network (Email-EUFootnote 7), the email network based on traffic data collected for 112 d at University of Kiel, Germany [7], and a mobile communication network [41]. Details are shown in Table 1. These networks are available publicly and some (such as Enron) have been extensively studied, but to our knowledge studies involving simplicial complexes and their properties have been non-existent with respect to these communication networks. While our primary goal here is not to study these properties for these specific networks, a secondary contribution of the results that follow is that they do shed some light on the extent and distribution of such complexes in these networks.

In the Introduction, we had introduced two separate (but related) research questions. Below, we discuss both individually, although both rely on a shared set of results.

RQ1: For each network, using the numbers of nodes and edges, and the observed average clustering coefficient, we generate 10 networks using the PA-based growth model (with TF). We obtain the frequency distributions (normalized to resemble a probability distribution) of adjacency factors of T*- and S*-complexes in both the real and generated networks, and visualize these distributions inFootnote 8 Fig. 2 and 3. Besides the direct comparison between the distribution curves, the figures suggest two functions that could fit the distributions (for the S*- and T*-complexes respectively):

$$\begin{aligned} f_{S*}(x; a, b, c) = c(bx^{-a})^{\log x} \end{aligned}$$
(1)
$$\begin{aligned} f_{T*}(x;\mu , \lambda , \sigma ) = \frac{\lambda }{2}e^{\frac{\lambda }{2}(2\mu +\lambda \sigma ^2-2x)}erfc(\frac{\mu +\lambda \sigma ^2-x}{\sqrt{2}\sigma }) \end{aligned}$$
(2)

where \(erfc(x) = \frac{2}{\sqrt{\pi }}\int _{x}^{\infty } e^{-t^2}dt\).

Both functional fits were discovered empirically using the Enron dataset as a ‘development’ set; however, as we show in response to RQ2, the functions fit quite consistently for all five datasets (but with different parameters, of course), although the first function diverges after a point (when the long tail begins). A theoretical basis for the functions is an interesting open question. We note that the second function is an Exponentially modified Gaussian (EMG) distribution, which is an important and general class of models for capturing skewed distributions. It has been broadly studied in mathematics, and has found empirical applications as well [11].

Table 2. Best-fit parameter estimates for Eq. 1 in both the real / generated network. The MND and reference baseline is described in the text.
Full size table
Table 3. Best-fit parameter estimates for Eq. 2 in both the real / generated network. The MND and reference baseline is described in the text.
Full size table

RQ2: We tabulate the best-fit parameters for each real world network, and the generated networks, in Table 2 and 3. For the real world networks, there is only one set of best-fit estimates. For the generated networks there are ten best-fit estimates per parameter (since we generate 10 networks per real-world network), for which we report the average in the table. We also compute a 2-tailed Student’s t-test and found that, for all parameters and all networks, the generated networks’ (averaged) parameter is significantly different from the corresponding real network’s best-fit parameter at the 99% level. This suggests, intriguingly, that despite the distributional similarities between Fig. 2 (a) and (b) (i.e., between the real and generated networks) the best-fit parameters are significantly different in both cases.

Of course, this does not answer the question as to whether the functions that we empirically discovered and suggested in Eqs. 1 and 2 are good approximations or models for the actual distributions. To quantify such a ‘goodness of fit’ between an actual frequency distribution curve (whether for the real network or the generated networks) and the curve obtained by using the models suggested in Eq. 1 or 2 (with best-fit parameter estimates), we compute a metric called Mean Normalized Deviation (MND). This metric is modeled closely after the root mean square error (RMSE) metric. Given an actual curve f and a modeled curve \(f'\), defined on a common supportFootnote 9 (x-axis) \(X=\{x_1, x_2, \ldots x_n\}\), the MND is given by:

$$\begin{aligned} \small MND(f,f', X) = \frac{1}{|X|} \sum _{x \in X} \frac{|f'(x)-f(x)|}{f(x)} \end{aligned}$$
(3)

Note that the lower the MND, the better \(f'\) fits f on support X. The MND can never be negative for a positive function f, but it has no upper bound. Hence, a reference is needed. Since we are not aware of any other candidate functional fits for the simplicial complex distributions in the literature, we use a simple (but functionally effective) baseline, namely the horizontal curve \(y=c\), where c is a constant that is selected to roughly coincide with the long-tail of the corresponding real network’s distribution.

In Table 2, we report not just the MNDs of the real and grown networks, but also the corresponding reference MND. Because of the significant long tails in Fig. 2, this MND is already expected to be low. We find, however, that with only three exceptions (over both equationsFootnote 10) for the generated networks (and none for the real networks) does the reference fit the actual distributions better than our proposed models (through a lower MND), despite being optimized to almost coincide with the long tail. Interestingly, Eq. 2 has (much) lower MND scores for the real network compared to the grown networks, as well as the reference function. As we noted earlier, Eq. 1 did not seem to be capturing the long tail accurately. We hypothesize that a piecewise function, where Eq. 1 is only used for modeling the short tail of the S*-complex frequency distribution, may be a better fit. In all cases, investigating the theory of this phenomenon is a promising area of investigation for complex systems research.

Fig. 4.
figure 4

The best-fit parameter a and \(\lambda \) in the estimated function of S*- (left) and T*-complexes (right) in generated networks with different numbers of nodes (N) and edges (M) configurations. P denotes the probability of TF step.

Full size image

In our exploration, we further visualized the relationship between the estimated function’s parameter of two simplices distribution and the configuration setting P of the generated network in Fig. 4. Intriguingly, despite variations in the configuration of the generated networks, the best-fit estimates seem to exhibit convergence behavior. Specifically, as different settings for the probability of TF steps in network generation are applied, the parameter, such as \(\lambda \) in T*-simplices distribution estimation, tends to stabilize towards a consistent value. This observed consistency may hint at some inherent properties of the two high-order structures. Such invariance across diverse network configurations not only underscores the potential utility and reliability of the parameter estimation but also points towards deeper, fundamental characteristics of these structures.

4 Conclusion

Simplicial complexes have become important in the last several years for modeling and reasoning about higher-order structures in real networks. Many questions remain about these structures, including whether they are captured properly by existing (and now classic) growth models. In this paper, we showed that, for two well-known complexes, the PA-model with triad formation captures the distributional properties of the complexes, but the best-fit parameters are significantly different between the grown networks and the real communication networks. It remains an active area of research to better understand the theoretical underpinnings of our proposed functional fits for the simplicial complex distributions, and also to deduce what could be ‘added’ to the growth model to bring its parameters into alignment with the real-world network. We are also investigating the properties of other growth models with respect to accurately capturing these distributions. Finally, understanding the real-world phenomena modeled by these complexes, which are fairly common motifs in all five networks we studied, continues to be an interesting research avenue in communication (and other complex) systems.