Keywords

1 Introduction

In the last two decades, a plethora of computational and experimental studies dealing with the design of biocompatible 3D printing scaffolds suitable for bone repair in severe fractures, have appeared in the literature [1,2,3,4]. However, despite the intensive work a clear answer on which is the proper scaffold’s structure that enhances cell viability and promotes cellular proliferation and differentiation has not been provided so far. Although well-tailored in vitro and in vivo experiments need to be carried out to answer the above question, computational models remain a robust tool for the design of those experiments due to their remarkable potential to explain and predict experimental results in scaffold-aided bone healing processes [5,6,7,8].

For long bones, the most popular computational model used for fracture healing predictions is by Prendergast [9], known as the mechanobioregulatory model, where the octahedral shear strain in the solid phase of the bone and the fluid velocity in the interstitial fluid phase are used as regulators of the tissue differentiation process [10,11,12]. Analogously, the mechanobioregulatory computational model of Prendergast has been exploited by many investigators for providing scaffold-aided bone regeneration predictions [13,14,15,16]. However, octahedral shear strain and interstitial fluid velocity concern cell differentiation regulators valid for the bone fracture biological environment and not for the initial cell proliferation and differentiation at the surface of a scaffold structure. At this early stage, all cells being attached at the surface of the scaffold experience only the surface deformation and the wall shear stress imposed by the loading of the scaffold and the surrounding interstitial flow, respectively. Therefore, Hendrikson et al. [15, 16] proposed the octahedral volumetric strains and interstitial fluid velocity be replaced by the new regulators corresponding to surface strains and shear wall stress, respectively.

Most of the scaffolds tested so far for tissue regeneration concern architectures with cylindrical fibers made of biocompatible polymers. All those 3D fused filament fabricated scaffolds are usually made up of layers containing parallel struts with the same or different orientation for each layer, with the most common being that with a 0/900 stacking sequence. However, such scaffolds appear problems associated with strut bending between two supports, disturbances of the shape and the volume of the pores, and degradation of the mechanical performance of the scaffold. To resolve this issue, multi-layer deposition of polymeric or particulate composite polymeric filaments has been adopted in the fabrication of rectangular and staggered 0/90 scaffolds [17,18,19,20,21,22,23]. Along with the filament deposition, strut’s material properties, and scaffold geometry, the pore size is an important parameter that influences drastically the scaffold-aided bone regeneration [24]. As it is mentioned in all cited works, scaffolds should exhibit mechanical properties that approach those of a physiological bone and adequate permeability to facilitate cell adhesion and proliferation, nutrient transport, and vascularization. Large, interconnected pores promote permeability but degrade the mechanical properties of the scaffold. Thus, scaffolds with multi-layer particulate composite polymeric filaments provide a compromised solution between mechanical and permeability requirements.

In the context of this work, the mechanoregulatory model of Hendrikson et al. [15, 16] is employed to explore the possible location of the early-stage cell attachment in a four-layer orthogonal scaffold with isometric pores made of polylactic acid PLA/316L with 5% stainless steel particle content when subjected to three-point bending. For the evaluation of surface strains and shear wall stresses, a hybrid computational mechanics framework is proposed based on conventional numerical simulation and Physics-Informed Neural Networks (PINNs) predictions. More precisely, the Boundary Element Method (BEM) is utilized to evaluate the displacement and the surface strain distributions at the surface points of the scaffold [25,26,27]. A PINN framework is further implemented, as a reduced order model (ROM), taking as input the surface displacement of the scaffold provided by the BEM boundary solutions and the material properties, to compute the displacement field in the internal domain of the scaffold [28, 29]. Moreover, the Element-based Finite Volume Method (EbFVM) [30] is utilized to simulate the Navier Stokes equations and calculate the velocity and wall shear stresses imposed by the interstitial blood flow at the surface of the scaffold. The goal of the present work is to show that conventional numerical methods like the BEM and EbFVM in conjunction with PINN algorithms are able, through mechanoregulatory models, to provide a robust numerical tool for scaffold-aided bone regeneration simulations.

The paper is structured as follows: Sect. 2 presents the geometry, the material composition, and the structure of the scaffold studied in the present work. Section 3 addresses in brief the numerical modeling of the problem via the BEM and the PINN, as well as the solution to the CFD problem with the EbFVM. Section 4 provides the numerical results dealing with the displacements, and the surface strain distribution, as well as the velocity, and wall shear stresses on the scaffold surface. These results are introduced in the mechanoregulatory model of Hendrikson et al. [15, 16] to provide predictions for the early-stage viability and differentiation of the cells attached at the surface of the scaffold. Finally, the main conclusions of the present work and thoughts about future steps are provided in Sect. 5.

2 Scaffold Design

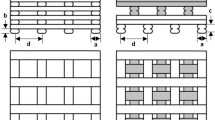
In this work, an orthogonal scaffold with a rectangular, four-layer strut design has been studied. The scaffold is composed of 9 filament rows, with a 0°/90° stacking sequence. Each strut is of width w = 0.142 mm and height h = 0.125 mm. The length of the scaffold is Ls = 3.375 mm, its width is Ds = 1.875 mm, and its height equals Hs = 1.125 mm. The distance between the struts is equal to 0.238 mm (Fig. 1i). The scaffold porosity percentage, defined by the volume of the scaffold and the total volume of a solid cube that has the same outline as the size of the designed scaffold, equals 65% [31].

Fig. 1.
figure 1

Geometric representation of the rectangular and four-layer scaffold. The geometric details of the designed scaffold are indicated in i) isometric, ii) upper side, and iii) left side view.

Full size image

The composite material of the scaffold is PLA enhanced with steel nanoparticles. PLA is a biodegradable polymer suitable for fabricating porous scaffolds in bone tissue engineering [20]. To improve the mechanical behavior of the PLA, steel particles are added into the PLA matrix, with specific content, and construct composite scaffolds. In the present work, the designed scaffold is made of PLA/316L with stainless steel particle content of 5 vol%. We consider that the steel particle number is large and randomly distributed and therefore, the composite material is assumed to be isotropic and linearly elastic. This is a realistic assumption since the cooling of each filament prevents the movement of the metallic powder inside and the four-layer composition of each strut ensures the uniform distribution of the steel particles in the internal space [22]. The Young modulus of the PLA when the steel powder is close to 5%, equals E = 0.28 GPa [32], while the Poisson ratio for the PLA is v = 0.37 [22].

This particular type of scaffold was chosen for the following reasons: (i) Due to the multi-layer fabrication of the rectangular struts and their reinforcement with steel particles, compromises pore size, mechanical performance, and blood flow requirements. (ii) The PLA/iron scaffold appears remarkable resistance against defect formation and layer delamination [22]. (iii) A PLA scaffold with a tetragonal structure presents the best mechanical behavior with quicker tissue growth compared to other scaffolds with different compositions and geometry [33]. (iv) The considered scaffold appears lower surface-to-volume ratio, compared to the corresponding one-layer rectangular scaffold, a fact that promotes better cell migration, proliferation, and differentiation [24].

3 Numerical Modeling

In this section, the computational tools and the problems solved to numerically study the designed scaffold are described. In the first subsection, a brief description of the BEM is provided, while in the second subsection, the PINN-based ROM framework employed for the fast computation of the displacements in the interior of the scaffold is presented. Finally, in the third subsection, the CFD tools, used to study the interaction of the scaffold with a fluid flow field, are briefly described.

3.1 Boundary Element Method (BEM)

In this work, the BEM is utilized for all the calculations regarding the structural behavior of the scaffold. The BEM is a robust numerical tool for solving linear elastic problems [26, 34]. Two well-known advantages of the BEM are the accurate evaluation of stresses and the dimensionality reduction of the problem since only the boundary of the domain needs to be discretized. In this section, the machinery for the numerical solution of elastostatic problems with the BEM is described.

The equilibrium equation for an isotropic and homogeneous linear elastic body is given as follows,

$$ \mu \partial_{ii} u_{i} \left( {\mathbf{x}} \right) + \left( {\lambda + \mu } \right)\partial_{j} \partial_{i} u_{i} \left( {\mathbf{x}} \right) = 0 $$
(1)

where \(u_{i} \left( {\mathbf{x}} \right)\) are the Cartesian components of the displacement vector at a point x of the elastic body with volume V and external boundary S, \(\partial_{i}\) denotes differentiation with respect to Cartesian coordinate \(x_{i}\), while λ and μ are the Lame parameters.

A well-posed boundary value problem for linear elasticity, requires appropriate boundary conditions for the displacement and traction vectors u and t, respectively, at the boundary S of the body, i.e.,

$$ \begin{aligned} u_{i} \left( {\mathbf{x}} \right) = & \overline{u}_{i} \left( {\mathbf{x}} \right), \, {\mathbf{x}} \in S_{u} \\ \,t_{i} \left( {\mathbf{x}} \right) = & \overline{t}_{i} \left( {\mathbf{x}} \right), \, {\mathbf{x}} \in S_{t} \\ \end{aligned} $$
(2)

where \(\overline{u}_{i}\), \(\overline{t}_{i}\) denote prescribed displacement and traction values with \(S_{u} \cup S_{t} = S\) and \(S_{u} \cap S_{t} = \emptyset\). The solution of Eq. (1) is represented in an integral form as follows [24],

$$ C_{ij} \left( {\mathbf{x}} \right)u_{j} \left( {\mathbf{x}} \right) + \int\limits_{S} {T_{ij}^{*} \left( {{\mathbf{x}},{\mathbf{y}}} \right)u_{j} \left( {\mathbf{y}} \right)dS_{{\mathbf{y}}} } = \int\limits_{S} {U_{ij}^{*} \left( {{\mathbf{x}},{\mathbf{y}}} \right)t_{j} \left( {\mathbf{y}} \right)dS_{{\mathbf{y}}} } $$
(3)

where \({\mathbf{x}}\) denotes the collocation point and \({\mathbf{y}}\) denotes the field point, while \(C_{ij} \left( {\mathbf{x}} \right)\) is the jump tensor obtaining the values \(C_{ij} \left( {\mathbf{x}} \right) = \delta_{ij}\) when \({\mathbf{x}} \in \Omega\), and \(C_{ij} \left( {\mathbf{x}} \right) = \frac{1}{2}\delta_{ij}\) when \({\mathbf{x}}\) belongs to a smooth part of the boundary \(S\), with \(\delta_{ij}\) denoting the components of the identity matrix. The expressions for the kernel tensor functions, \(U_{ij}^{*} \left( {{\mathbf{x}},{\mathbf{y}}} \right)\) and \(T_{ij}^{*} \left( {{\mathbf{x}},{\mathbf{y}}} \right)\), appearing in Eq. 3 can be found for 3D elastic problems in [34, 35].

In the BEM formulation, integral Eq. (3) is utilized along with the boundary conditions (2) for the solution of the problem. Assuming that the boundary of the body is discretized into \(N_{E}\) boundary elements, with each element e defined by \(N_{F}^{\left( e \right)}\) nodes, Eq. (3) obtains the following form for a collocation point \({\mathbf{x}}_{k}\):

$$ {\mathbf{C}}_{k} {\mathbf{u}}_{k} + \sum\limits_{e = 1}^{{N_{E} }} {\sum\limits_{i = 1}^{{N_{F}^{\left( e \right)} }} {{\mathbf{H}}_{kei} \cdot {\mathbf{u}}_{i} } } = \sum\limits_{e = 1}^{{N_{E} }} {\sum\limits_{i = 1}^{{N_{F}^{\left( e \right)} }} {{\mathbf{G}}_{kei} \cdot {\mathbf{t}}_{i} } } $$
(4)

where \({\mathbf{u}}_{k} = {\mathbf{u}}\left( {{\mathbf{x}}_{k} } \right)\), and the matrices \({\mathbf{H}}_{kei}\) and \({\mathbf{G}}_{kei}\) contain the integrals appearing in Eq. (3). A challenge for the application of BEM is the computation of the boundary integrals, which exhibit singular behavior when \({\mathbf{x}} \to {\mathbf{y}}\) [34]. Collocating Eq. (4) for all the nodes of the boundary the following linear system of equations can be obtained:

$$ {\mathbf{H}} \cdot {\mathbf{u}} = {\mathbf{G}} \cdot {\mathbf{t}} $$
(5)

where the vectors \({\mathbf{u}}\) and \({\mathbf{t}}\) contain all the displacements and tractions for the nodes of the boundary. By applying the boundary conditions of the problem, a linear system of equations \({\mathbf{A}} \cdot {\mathbf{x}} = {\mathbf{b}}\) is obtained, where the matrix \({\mathbf{A}}\) is dense and non-symmetric.

In the conventional BEM, the fully populated matrix \({\mathbf{A}}\) requires O(N2) operations for its buildup and O(N3) operations for the solution of the final linear system of equations through typical LU-decomposition solvers. The dense nature of the A matrix has traditionally confined the BEM to small-scale problems, where the degrees of freedom N cannot be more than a few hundred of thousand. To overcome this limitation, various accelerated BEM implementations have been proposed, employing hierarchical matrices and Adaptive Cross Approximation (ACA) techniques [26, 36,37,38,39], combined with an iterative Generalized Minimum Residual (GMRES) solver. These BEM implementations, partition the geometry into clusters and utilize algebraic or hybrid algorithms to compress the submatrices of \({\mathbf{A}},\) which contain the values of the integrals corresponding to certain cluster combinations of collocation points and boundary elements. Using these techniques, the assembly time for the matrix \({\mathbf{A}}\), the required memory for its storage, as well as the solution time of the final linear system of equations can be significantly reduced.

In a post-processing step, using Eq. (3) with \(C_{ij} = \delta_{ij}\) the displacement of an interior point \({\mathbf{x}}\) can be calculated, using the previously computed boundary values of the tractions and the displacements. Furthermore, for a point \({\mathbf{x}}\), lying on a smooth part of the boundary, the strain can be calculated through the displacement gradient computed with the following integral equation [35],

$$ \frac{1}{2}\partial_{k} u_{i} \left( {\mathbf{x}} \right) + \int\limits_{S} {P_{kij}^{*} \left( {{\mathbf{x}},{\mathbf{y}}} \right)u_{j} \left( {\mathbf{y}} \right)dS_{{\mathbf{y}}} } = \int\limits_{S} {Q_{kij}^{*} \left( {{\mathbf{x}},{\mathbf{y}}} \right)t_{j} \left( {\mathbf{y}} \right)dS_{{\mathbf{y}}} } $$
(6)

which can be derived by applying the gradient operator to Eq. (3). Having computed the displacement gradient, the strain is given as \(\varepsilon_{ij} \left( {\mathbf{x}} \right) = \frac{1}{2}\left( {\partial_{i} u_{j} \left( {\mathbf{x}} \right) + \partial_{j} u_{i} \left( {\mathbf{x}} \right)} \right)\). The mathematical expressions for the tensor kernels \(P_{kij}^{*} \left( {{\mathbf{x}},{\mathbf{y}}} \right)\) and \(Q_{kij}^{*} \left( {{\mathbf{x}},{\mathbf{y}}} \right)\) are given in [34, 35].

Fig. 2.
figure 2

Boundary conditions and mesh grid of the designed scaffold for the numerical solution of the structural problem.

Full size image

To simulate a three-point bending loading scenario of the scaffold structure, a vertical compressive load is imposed on the upper, central face of the scaffold with magnitude p = 5 MPa, as it is shown in Fig. (2). The bottom left and right faces of the scaffold are kept fixed. For the BEM simulation, an in-house developed software using fast solvers for integral equations is employed [26, 39].

3.2 Physics-Informed Neural Networks (PINNs)

In recent years, ROMs [40] or deep learning-based solvers, such as PINNs [41] are commonly employed to obtain approximate solutions for parameterized, large-scale PDEs in a limited amount of time. A PINN is a meshless method for solving PDEs that utilizes an artificial neural network (ANN) to approximate in an unsupervised or semi-supervised manner the solution of a boundary value problem [42]. The method integrates the information from the physical laws of the boundary value problem, by including the PDEs that described the problem in the loss function during the training of the ANN.

In general, an ANN, also known as a multi-layer perceptron, approximates the functional relation among a set of inputs and outputs. It contains several layers with numerous neurons. The first and last layers represent the input and output layers, respectively and the intermediate layers are called hidden layers. When the ANN contains more than one hidden layer, it is called a deep neural network. Each layer performs a transformation by combining a linear mapping, with the application of a non-linear activation function. Based on a well-known extension of the universal approximation theorem, an ANN consisting of an arbitrary number of hidden layers, each of them containing an arbitrary number of neurons, can approximate a function with respect to some accuracy.

In the frame of this work, a multilayer ANN is employed for the fast computation of the displacements at the interior of the scaffold, taking as input the coordinates, the material properties, and the pressure load combined in a single vector \({\mathbf{x}}_{I} = (x,y,z,E,\nu ,p)\) while predicting the displacement vector \({\tilde{\mathbf{u}}} = (\tilde{u},\tilde{v},\tilde{w})\). The ANN approximation can be expressed as follows,

$$ {\mathbf{u}}({\mathbf{x}}_{I} ) \approx {\tilde{\mathbf{u}}}({\mathbf{x}}_{I} ) = \varphi_{f} ({\mathbf{x}}_{I} ;{\mathbf{w}}_{f} ,{\mathbf{b}}_{f} ) $$
(7)

where \({\mathbf{w}}_{f} ,{\mathbf{b}}_{f}\) are the vectors containing the weight and bias parameters, and \(\varphi\) is a (non)-linear mapping \(N:{\mathbf{\mathbb{R}}}^{6} \to {\mathbf{\mathbb{R}}}^{3}\). The entries of the weight matrices and bias vectors constitute the parameters of the neural network \([{\mathbf{w}}_{f} ,{\mathbf{b}}_{f} ]\), which are computed using optimization techniques so that the neural network approximates the functional relation of interest with respect to certain criteria imposed by a predefined loss function. The derivatives of the ANN parameters can be calculated with automatic differentiation using well-known libraries (e.g., PyTorch, TensorFlow).

In the context of this work, to include the equations related to the physics of the problem in the training of the PINN, the PDE along with the boundary conditions are incorporated into the loss function. More specifically, a PINN framework is implemented to predict the solution of the homogenous Navier-Cauchy equations (Eqs. 1, 2), and provide the displacement distribution in the interior of the scaffold geometry (Fig. 4). The developed PINN framework is further used as ROM since the ANN is trained by including the material properties and the bending load to the input vector. The loss function that includes the governing equations and the boundary conditions can be expressed as [28, 29, 43, 44],

$$ L = L_{PDE} + L_{BC} $$
(8)

Regarding the loss of the boundary conditions, we get the numerical solution of the variable u on the boundaries from the BEM solutions. Therefore the \(L_{BC}\) term obtains the following form:

$$ L_{BC} = \,\frac{1}{{N_{bc} }}\sum\limits_{i = 1}^{{N_{bc} }} {[(\tilde{u} - u^{BEM} )^{2} } + (\tilde{v} - v^{BEM} )^{2} + (\tilde{w} - w^{BEM} )^{2} ]_{(i)} $$
(9)

where \(u^{BEM} ,v^{BEM} ,w^{BEM}\) are the data provided by the high-fidelity BEM solutions on the boundaries and \(N_{bc}\) is the number of the training points uniformly sampled from the mesh on the scaffold surface. While the loss derived from the PDE, \(L_{PDE}\) is written as follows (Fig. 3),

$$ \begin{aligned} L_{PDE} = & \frac{1}{{{\rm N}_{p} }}\sum\limits_{i = 1}^{{{\rm N}_{p} }} {\left[ {\left( {\mu \left( {\frac{{\partial^{2} \tilde{u}}}{{\partial x^{2} }} + \frac{{\partial^{2} \tilde{u}}}{{\partial y^{2} }} + \frac{{\partial^{2} \tilde{u}}}{{\partial z^{2} }}} \right) + (\lambda + \mu )\left( {\frac{{\partial^{2} \tilde{u}}}{{\partial x^{2} }} + \frac{{\partial^{2} \tilde{\upsilon }}}{\partial y\partial x} + \frac{{\partial^{2} \tilde{w}}}{\partial z\partial x}} \right)} \right)^{2} } \right.} + \\ & \left( {\mu \left( {\frac{{\partial^{2} \tilde{\upsilon }}}{{\partial x^{2} }} + \frac{{\partial^{2} \tilde{\upsilon }}}{{\partial y^{2} }} + \frac{{\partial^{2} \tilde{\upsilon }}}{{\partial z^{2} }}} \right) + (\lambda + \mu )\left( {\frac{{\partial^{2} \tilde{u}}}{\partial x\partial y} + \frac{{\partial^{2} \tilde{\upsilon }}}{{\partial y^{2} }} + \frac{{\partial^{2} \tilde{w}}}{\partial z\partial y}} \right)} \right)^{2} + \\ & \left. {\left( {\mu \left( {\frac{{\partial^{2} \tilde{w}}}{{\partial x^{2} }} + \frac{{\partial^{2} \tilde{w}}}{{\partial y^{2} }} + \frac{{\partial^{2} \tilde{w}}}{{\partial z^{2} }}} \right) + (\lambda + \mu )\left( {\frac{{\partial^{2} \tilde{u}}}{\partial x\partial z} + \frac{{\partial^{2} \tilde{\upsilon }}}{\partial y\partial z} + \frac{{\partial^{2} \tilde{w}}}{{\partial z^{2} }}} \right)} \right)^{2} } \right]_{(i)} \\ \end{aligned} $$
(10)

where \(N_{p}\) is the number of the training points uniformly sampled from the scaffold mesh. Where the notation \((i)\) denotes that the function is applied for each point \(i.\)

Fig. 3.
figure 3

Schematic diagram of the PINN framework for the Navier-Cauchy equations. The PINN is used as a ROM, taking as inputs the coordinates, the material properties, and the boundary conditions, derived through the BEM, aiming to predict the deformation in the scaffold domain.

Full size image

The adaptive moment estimation (ADAM) optimizer, a version of stochastic gradient descent is utilized for the optimization process of the ANN. The PINN is trained for 10000 epochs, with a batch size of 2000 and a learning rate equal to 0.001. All the parameters of the ANN are tuned using a hypermeter optimization analysis. Regarding the ANN architecture, 10 hidden layers are employed, each including 30 neurons, selected in an ad-hoc manner, while the tanh is used as an activation function. Regarding the computational times, the BEM needs 30 min to compute a high-fidelity solution and provide the boundary results to the PINN framework. The PINN requires 1 h of training using an Intel Core i7 @ 2.20GHz, NVIDIA Ge-Force GTX 1050 Ti GPU computer.

3.3 Element-Based Finite Volume Method (EbFVM)

As a second step, we examine the interaction of the scaffold with a fluid flow to further elucidate the mechanism of the scaffold design in the early-stage cell differentiation procedure. The objective is to compute the distribution of the wall shear stress on the scaffold surface, as this is a quantity that is often linked to the differentiation of the cells on the scaffold [16, 45]. To this end, high-fidelity CFD simulations are performed with the EbFVM [30], using the flow solver available in the commercial software SIEMENS Simcenter 3D.

The steady-state incompressible fluid flow within a volume \(\Omega \subset {R}^{d}\), satisfies the Navier-Stokes equations,

$$ \rho {\mathbf{v}}\left( {\mathbf{x}} \right) \cdot \nabla {\mathbf{v}}\left( {\mathbf{x}} \right) + \nabla p\left( {\mathbf{x}} \right) - \mu \nabla^{2} {\mathbf{v}}\left( {\mathbf{x}} \right) = {\mathbf{0}}, \, {\mathbf{x}} \in \Omega $$
(11)
$$ \nabla \cdot {\mathbf{v}}\left( {\mathbf{x}} \right) = 0, \, {\mathbf{x}} \in \Omega $$
(12)

where \({\mathbf{v}}\left( {\mathbf{x}} \right):\Omega \to R^{d}\), is the velocity field,\(\rho\) is the fluid density, \(p\left( {\mathbf{x}} \right):\Omega \to R\) is the pressure field, and \(\mu \in R^{ + }\) is the dynamic viscosity.

We consider a Newtonian fluid with density ρ = 1000 \(kg/{m}^{3}\) and dynamic viscosity \(\mu = 0.001 \, Pa \cdot s.\) The laminar inlet flow is perpendicular to the top plane of the scaffold, with a magnitude \(v_{in} = 3 \, mm/s\). Symmetry conditions are imposed on the z-axis to decrease the computational time, and zero pressure on the outlet face, while no-slip condition (zero velocity) is applied to the remaining boundary faces (Fig. 4).

Fig. 4.
figure 4

Mesh grid of the designed scaffold and boundary conditions for the computational fluid dynamics problem.

Full size image

4 Numerical Results

In this section, the numerical results of the computational mechanics simulations including the CSM and CFD solutions using the BEM, the PINN, and the EbFVM around the scaffold geometry are presented.

4.1 Computational Structural Mechanics (CSM) Analysis

In this subsection, the main results are presented for the structural behavior of the scaffold. Regarding the utilized mesh grid, it consists of 1,010,880 isoparametric, linear, quadrilateral elements and 1,010,200 nodes on the scaffold surface (Fig. 2). The mean element size of the discretization is equal to 0.01mm and has been derived after a convergence analysis. The resulting number of degrees of freedom for this problem is about 3 million and cannot be solved with the conventional BEM. To overcome this problem a BEM implementation based on Hierarchical Matrices and ACA has been employed [26, 39]. For the solution of the final linear system of equations, the GMREs iterative solver has been utilized.

Fig. 5.
figure 5

Displacement magnitude obtained through the BEM and the PINN on the scaffold geometry (top) and the half (bottom). The results are scaled x2 to better visualize the results.

Full size image

In Fig. 5 the magnitude of the displacement computed through the BEM simulations, as well as the PINN results obtained using the BEM boundary solutions, are provided. The PINN framework is utilized as a ROM aiming to provide the solution in the scaffold domain given the material properties and the boundary conditions. In particular, the high-fidelity solution of the BEM on the scaffold surface is given as a boundary condition to the PINN framework. To compare the BEM and PINN results in the domain with the BEM, based on the surface mesh we generate a volume mesh for the scaffold. In a second step, the displacements at the interior nodes are obtained with the BEM in a post-processing step using Eq. (3), since the displacements and tractions at the boundary of the domain have already been computed. Similarly, the PINN is utilized for the computation of the displacements on the interior nodes of the scaffold. The results for both methods, presented in Fig. 5, are in very good agreement. As expected, the larger values of the displacement are obtained on the top middle strut of the filament row, located on the region of the bending load.

As soon as the surface displacements and the tractions are known, using Eq. (6) the strains are evaluated with BEM for the boundary points. The computed strains are then transformed, to calculate the surface shear strain on each element face defined as follows [16],

$$ \gamma_{srf} = \frac{1}{2}\left( {\varepsilon_{1} - \varepsilon_{2} } \right) $$
(13)

where \(\varepsilon_{1}\) and \(\varepsilon_{2}\) are the principal strains on the element surface. To compute the principal strains on the surface of each element the strain tensor is rotated with respect to a coordinate system \(\left( {{\mathbf{n}},{\mathbf{s}}_{1} ,{\mathbf{s}}_{2} } \right)\) where n is the unit normal vector of each element, and \({\mathbf{s}}_{1}\),\({\mathbf{s}}_{2}\) are the unit vectors on the plane of each element. The orthogonal projection of the rotated strain tensor on the surface of the element is the \(2 \times 2\) part of the rotated matrix with components corresponding to the unit vectors \({\mathbf{s}}_{1}\) and \({\mathbf{s}}_{2}\). The obtained eigenvalues of this matrix are the values of \(\varepsilon_{1}\) and \(\varepsilon_{2}\) used in Eq. (13).

The calculated surface shear strains are presented in Fig. 6. It is shown that significant surface strains are obtained as expected in the middle strut of each filament row due to the increased deformations in that region. The results reveal a more localized surface strain distribution, at the crossings of the fibers with a pick value close to 0.1. This is to be expected, due to the non-uniform, bending loading condition.

Fig. 6.
figure 6

Surface strain distribution on the scaffold geometry obtained by the BEM solution.

Full size image

4.2 Computational Fluid Dynamics (CFD) Analysis

In this section, the velocity, and wall shear stress distributions imposed by the fluid flow on the scaffold surface are presented. A fine mesh grid has been employed for the CFD analysis, including 26,219,072 tetrahedral solid elements, resulting in 4,620,051 nodes. A local refinement is used near the scaffold area, with the mean element size being equal to 0.01 mm (Fig. 4).

In Fig. 7, the magnitude of the velocity contour in the domain is presented. It is observed that the maximum velocity is approximately six times higher than the inlet velocity, indicating the acceleration of the blood flow due to the variability in the inlet area and the scaffold region [46]. Observing the streamlines contour, leads us to consider that the geometry and the inlet velocity, significantly affect the blood flow within the scaffold.

Fig. 7.
figure 7

Velocity contour on the scaffold geometry obtained through the CFD analysis.

Full size image

In Fig. 8 the wall shear stresses of the fluid flow on the scaffold geometry are displayed. High values are observed on the top faces of each strut along the filament row, and side faces of the scaffold. The pick values are obtained on those faces, which are parallel to the fluid flow, and further present the largest velocity values (Fig. 7) [47]. The wall shear stress distribution is uniform, with a maximum value close to 0.9 Pa.

Fig. 8.
figure 8

Wall shear stress contour on the scaffold geometry obtained through the CFD analysis.

Full size image

4.3 Mechanoregulatory Model for the Early-Stage Cell Differentiation

The cell differentiation on the scaffold surface can be computed based on the following mechanoregulatory model [16] which considers both the surface shear strain, and the fluid wall shear stress as follows,

$$ S = \frac{{\gamma_{srf} }}{\alpha } + \frac{\tau }{b} $$
(14)

where \(S\) is the cell stimulus, \(\gamma_{srf}\) is the surface strain calculated in Ch. 4.1, \(\tau\) is the wall shear stress obtained in Ch. 4.2, while \(a = 0.0375\) and \(b = 0.01\,Pa,\) are constants influencing the behavior of the model [16] (Fig. 9). Based on the cell stimulus values the cell types on the surface of the scaffold are characterized [16]. In particular, the cell stimulus S values thresholds are \(0 \le S < 0.001\) for resorption, revealing that in this case the cell stimulus is too low and cannot induce any differentiation to the cell, \(0.001 \le S < 1\) for bone generation, \(1 \le S < 3\) for cartilage, \(3 \le S < 6\) for fibrous tissue, and \(S \ge 6\) for necrosis, indicating that the stimuli are too intense to induce any differentiation.

Fig. 9.
figure 9

Cell differentiation stimulus distribution on the scaffold surface.

Full size image

In Fig. 9, it is observed the highest values of the cell stimulus are observed on the regions of the pick wall shear stress. Therefore, the utilized cell differentiation prediction model [16], based on a combination of the surface shear stress and the wall shear stress, reveals that for the current loading setup, the fluid flow affects more the cell stimulus value than the bending load. In particular, based on the obtained values of the surface shear strain and the fluid wall shear stress, for a distribution of cells on the scaffold, about 0.67% of the cells would correspond to resorption, 45.56% to bone, 9.58% to cartilage, 6.60% to fibrous tissue and 37.56% to necrosis.

5 Conclusions

In the present work, an innovative, hybrid methodology based on numerical simulation and deep learning is developed, to study the mechanical behavior of a composite scaffold made of PLA/316L with 5% stainless steel particle content. The BEM was used to evaluate the structural behavior of the scaffold when a bending load is applied and compute the displacement and the surface shear strain on the scaffold. It is shown that the BEM is an ideal methodology for the calculation of the surface strain for a linear elastic material. Furthermore, a PINN framework is developed as a ROM to provide the solution given the materials properties and the boundary conditions. It is proven that the PINN is a promising methodology for constructing reduced order models which explicitly incorporate the physics of the problem, while its training can be achieved by utilizing information obtained from numerical methods such as the BEM. In terms of accuracy, both the BEM and PINN results of the displacements in the scaffold domain are in good agreement.

Regarding the CFD calculations, the obtained wall shear stress has higher values in the areas parallel to the fluid flow. The predicted CFD and CSM results are used to exploit the efficiency of the scaffold design by calculating the cell differentiation stimulus and obtaining the regions of possible tissue development. It is shown that for the developed numerical approach and the designed geometry, most of the scaffold surface is predicted in the bone generation while the minority belongs to resorption.

Future steps, amongst others, include the implementation of ROMs for the calculation of the surface strains and the wall shear stresses for various material properties, pores size, and boundary conditions.