Change Point Detection for Time Dependent Counts Using Extended MDL and Genetic Algorithms

Abstract

This article introduces an extension for change point detection based on the Minimum Description Length (MDL) methodology. Unlike traditional approaches, this proposal accommodates observations that are not necessarily independent or identically distributed. Specifically, we consider a scenario where the counting process comprises observations from a Non-homogeneous Poisson process (NHPP) with a potentially non-linear time-dependent rate. The analysis can be applied to the counts for events such as the number of times that an environmental variable exceeded a threshold. The change point identification allows extracting relevant information on the trends for the observations within each segment and the events that may trigger the changes. The proposed MDL framework allows us to estimate the number and location of change points and incorporates a penalization mechanism to mitigate bias towards single regimen models. The methodology addressed the problem as a bilevel optimization problem. The first problem involves optimizing the parameters of NHPP given the change points and has continuous nature. The second one consists of optimizing the change points assignation from all possible options and is combinatorial. Due to the complexity of this parametric space, we use a genetic algorithm associated with a generational spread metric to ensure minimal change between iterations. We introduce a statistical hypothesis t-test as a stopping criterion. Experimental results using synthetic data demonstrate that the proposed method offers more precise estimates for both the number and localization of change points compared to more traditional approaches.

1 Introduction

Identifying change points in time series is paramount for several analysis that helps understanding the underlying dynamic or performing some practically capital tasks as forecasting. A prime example of the latter is on the scenario of cybersecurity, where the focus lies in monitoring the instances of breaching a predefined threshold for data transfer volume over a network. This study employs a cutting-edge model for identifying the number of change point and their values in a time series of counts, such as the threshold breaches as a function of time.

The literature consistently emphasizes a fundamental flaw in many models designed to detect change points in time series. These models tend to assume equal and independent distribution of the data points within a segment, which fundamentally contradicts their inherent nature. As eloquently discussed in [9], this research endeavor ingeniously sidesteps the aforementioned assumption by considering a flexible family of non-homogeneous Poisson processes.

This investigation leverages a genetic algorithm to ascertain the optimal solution for the time series groupings (segments) in the overall observation time interval. A possible grouping is ingeniously represented as individuals (also referred to in the literature as chromosomes, creatures, or organisms) consisting of binary vectors, with a value of one indicating the time when we have a change point and zero otherwise. The evolutionary principles of selection, mutation, mating, evaluation, and replacement are deftly applied, drawing inspiration from the realms of probability, Bayesian computational methods, and information theory.

Pre-specifying the number of generations originated by the algorithm can lead to unnecessary evaluation of the objective function, [14]. In this study, a judicious stopping criterion is established, underpinned by a simple yet effective decision rule involving a t statistic. Moreover, this research achieves a higher rate of accurately pinpointing the number and location of change points, employing the same principle as in [14], which relies on counting the exceedances to a threshold value instead of using the measurements per se. Additionally, the algorithm provides insights into the composition of the intensity function parameters governing the Non-Homogeneous Poisson process (NHPP), shedding light on the non-linear tendencies inherent in the observational emission patterns.

In this work we assume that the NHPP has a decaying and non-linear intensity described by a Weibull distribution, however, the methodology can easily be extended to broader cases that can include some other possible families of intensities. The decision to adopt the Weibull distribution as the intensity function is primarily based on the interpretative potential of the Weibull’s shape parameter and the wealth of experience gained from prior seminal works such as [1,2,3], and [13].

Through computation experiments, we observe that this approach exhibits superior efficacy in identifying change points, particularly when confronted with extreme data scenarios.

2 Non-homogeneous Poisson Process

A Non-Homogeneous Poisson process (NHPP) extends the ordinary Poisson process allowing the average rate can vary with time. Many applications that generate counts (random points) are more faithfully modeled with such NHPP with the cost of losing the practically convenient property of stationary increments.

NHPPs are an excellent tool for modeling counting processes of the number of occurrences at time t due to their easy interpretability. In particular, the focus of this study is to count the number of times a threshold is exceeded, with each occurrence referred to as an “exceedance”. Therefore, this process generates a new series of count observations that records, per unit of time, the number of exceedance up to t, denoted as N(t).

We consider the stochastic process N(t) as an NHPP, where the increments $N(t+s)-N(t)$ follow a Poisson distribution with a parameter $\left( m(t+s)-m(t)\right)$ that depends on time t. This condition allows for the change points identification without assuming that the observations are equally distributed. Therefore, the probability that starting at time t, the time to the next exceedance is greater than a length of time s is denoted as G(t; s). In other words, the probability of no exceedances occurring in the interval $(t,t+s]$ is given by

$$ G(t;s)=P(N(t+s)-N(t)=0)=\exp \left\{ -[m(t+s)-m(t)]\right\} . $$

Then, the probability that starting at time t, the time to the next exceedance is less than s is given by

$$ F(t;s)=1-G(t;s)=1-\exp \left\{ -[m(t+s)-m(t)]\right\} . $$

The probability density function of the interval to the next exceedance is denoted as

$$ f(t;s)=\lambda (t+s)\exp \left\{ -[m(t+s)-m(t)]\right\} , $$

where $\lambda (t)$ is the intensity function that characterizes an NHPP and relates to the process parameters as

$$\begin{aligned} m(t_{i+1})-m(t_{i})=\int _{t_i}^{t_{i+1}}\lambda (u)du. \end{aligned}$$

(1)

According to [5], for time-dependent Poisson processes, the intervals between successive events are independently distributed. The probability, starting at $t_i$, that the next exceedance occurs in the interval $(t_{i+1},t_{i+1}+\varDelta t]$ is given by

$$\begin{aligned} \lambda (t_{i+1})\exp \left\{ -[m(t_{i+1})-m(t_{i})]\right\} \varDelta t+o(\varDelta t) \end{aligned}$$

(2)

If a series of successive exceedances is observed in the time interval (0, T], occurring at $\textbf{D}=\{t_1,t_2,\ldots ,t_n\}$, the likelihood function, which will be part of the objective function in the genetic algorithm, is expressed as

$$\begin{aligned} \left[ \prod _{i=1}^{n} \lambda (t_{i})\exp \left\{ -[m(t_{i})-m(t_{i-1})]\right\} \right] \exp \left\{ -[m(T)-m(t_{n})]\right\} , \end{aligned}$$

(3)

with $t_0=0$. The last element in (3) is the survival probability $G(t_n; (T-t_n))$ since the interval $(t_{n},T]$ do not register any exceedance.

Since $m(0)=0$ and $m(T)=\int _{0}^{n}\lambda (u)du$, we can simplify the previous likelihood to

$$ L(\textbf{D}|\phi ) \propto \left\{ \prod _{i=1}^{n}\lambda (t_{i})\right\} \exp \left\{ -m(T)\right\} . $$

The parameter $\phi$ specify the model and it is present in the intensity $\lambda (t)$ and cumulative mean, m(t). Hence we can explicitly express this fact using the following expression for the likelihood

$$\begin{aligned} L(\textbf{D}|\phi ) \propto \left\{ \prod _{i=1}^{n}\lambda (t_{i}\mid \phi )\right\} \exp \left\{ -m(T\mid \phi )\right\} . \end{aligned}$$

(4)

The estimation of parameters $\phi$ is one of the main objectives of this study. However, there is another key characteristic we want to infer and this is the point where we can have regimen changes (hence different $\phi$ values). These points are called change points and we denoted them as $\boldsymbol{\tau }=\{\tau _1,\tau _2,\ldots ,\tau _J\}$, $J\in \mathbb {N}$, where $0\le \tau _i\le T$ for $i=1,\ldots ,J$.

The overall likelihood based on the observations $\textbf{D}$ during the period of time (0, T] of a NHPP with known change points $\boldsymbol{\tau }$ corresponds to

$$\begin{aligned} L(\textbf{D}|\phi , \boldsymbol{\tau }) \propto & \left[ \prod _{i=1}^{N_{\tau _1}}\lambda (t_i\ | \ \phi _1) \right] \exp \left\{ -m(\tau _1 | \phi _1)\right\} \nonumber \\ & \times \left[ \prod _{j=2}^{J} \left( \prod _{i=N_{\tau _{j-1}}+1}^{N_{\tau _j}}\lambda (t_i |\phi _j)\right) \exp \left\{ -[m(\tau _j |\phi _j)-m(\tau _{j-1} | \phi _{j-1} )]\right\} \right] \nonumber \\ & \times \left[ \prod _{i=N_{\tau _{J}}+1}^{n}\lambda (t_i|\phi _{J+1})\right] \exp \left\{ -[m(T |\phi _{J+1})-m(\tau _{J}|\phi _{J} )]\right\} , \end{aligned}$$

(5)

where $N_{\tau _i}$ is the cumulative number of observations up to time $\tau _i$, $\phi _i$ is the parameter that describes the NHPP during $(\tau _{i-1},\tau _i]$, $i=1,\ldots , n$, (with $\tau _0=0$), and $\phi _{J+1}$ describes the NHPP during the last observe regimen in $(\tau _{n},T]$. For more details see [13].

If we know the change points number and location, as in (5), we can select the parameter $\phi$ that characterize the model that better fit the data using the Bayesian paradigm. The log-posterior distribution, that describes the updated information on the parameter $\phi$ is

$$\begin{aligned} \ln f(\phi |\textbf{D}, \boldsymbol{\tau })\propto \ln (L(\textbf{D}|\phi , \boldsymbol{\tau })) + \ln (f(\phi | \boldsymbol{\tau })), \end{aligned}$$

(6)

where $f(\phi |\textbf{D}, \boldsymbol{\tau })$ is the posterior distribution and $L(\textbf{D}|\phi , \boldsymbol{\tau })$ is the likelihood (5) regarding the parameter $\phi$ as the variable, and $f(\phi | \boldsymbol{\tau })$ contains the prior information we have on the real value of $\phi$ for given values of $\boldsymbol{\tau }$.

The expression (6) defines the posterior distribution for the parameters, and we use the value of the parameter that maximizes it. This is called the maximum a posteriori or MAP. With the genetic algorithm approach, we compute the MAP among each generation and use them to compute to select the best individuals for the following generation.

Now we proceed to describe the proposed method for the overall model with unknown change points. For this, we require to determine the change points $\boldsymbol{\tau }$ before estimating the rest of the parameters involved. That is, the first step is selecting the number and location of the change points. This involves a model selection that will be handled with by the MDL approach.

3 MDL

The Minimum Description Length (MDL) combines Occam’s razor and information theory to determine the model that better fits the data. It first appeared on [11], but has been widely explored both theoretically [7] and in many popular applications such as PCA [4].

In the early days of mathematical modeling, simple models, such as linear ones, were the only ones explored to ‘fit’ the data. Since then, not only richer models are being used but also some different criteria for selecting their parameters have been developed. One of them is rooted in the information theory, which focuses on encoding the data to describe the contained information. From a computational point of view, data is encoded in many ways which include arrays, matrices, and many kinds of structures. However, any kind of representation costs a number of bits in memory space, this number of bits is what we call the code length. Different representations might require a different code length and when encoding data, shorter codes are preferred over longer ones as they take less memory space. For efficiency, one of the main tasks consist in assigning a model that has the shortest code and in the change point detection problem, we need to encode the number and location of the change points, as well as the model to fit the data within each regimen between consecutive change points. The MDL principle is used to give a numeric value to the code length associated with different assignations of the change points.

The MDL code length is divided into two summands.

$$\begin{aligned} MDL(\boldsymbol{\tau }) = -\ln {f(\hat{\phi }|\textbf{D},\boldsymbol{\tau })} + P(\boldsymbol{\tau }). \end{aligned}$$

(7)

The first summand is a term related to the fitted model considering the data and selected change points $\boldsymbol{\tau }$. This term corresponds to the negative of the logarithm of the MAP for $\phi$ and measures how well the model fits the data on each regimen, given $\boldsymbol{\tau }$. When considering the model associated with the posterior (6), we notice that the length of the parameter $\phi =(\phi _1,...,\phi _J)$ is fixed if we know the number of change points $|\boldsymbol{\tau }|=J$. However, as $\boldsymbol{\tau }$ is also a parameter to fit, the parametric space for $\phi$ must consider spaces with different dimensions. That is, the number of parameters is not constant. For estimating all parameters $\phi$ and $\boldsymbol{\tau }$, in the complex parametric space they are defined, we use a non-parametric approach to select $\boldsymbol{\tau }$ and then we harness the posterior distribution and MAP to establish a criterion for selecting all the parameters using (7).

Fixing the number of change points, we stablish the number of parameters required, however, we still have to determine where to locate them as the posterior depends on it to be properly defined. The second summand in (7) is meant to control both, the number of change points and their location. It can be seen as a penalization function that increases with the number of parameters that are to be encoded in the model and their location in the selected model. Explicitly, the penalization function takes the form of (8) which is an upgrade from [14].

$$\begin{aligned} P(\boldsymbol{\tau ^*}) = R \sum _{i=1}^{j^*+1} \frac{\ln {(\tau _i^*-\tau _{i-1}}^*)}{2} + \ln {(j^*+1)} + \sum _{i = 2}^{j^*} \ln (\tau _i^*), \end{aligned}$$

(8)

where $\boldsymbol{\tau ^*}=(\tau _1^*,\ldots ,\tau _{j^*}^*)$ is a set of possible change points with $j^*$ different elements, and R is the number of parameters the model has on each regimen.

In [14], the term $\ln (j^*+1)$ was $\ln (j^*)$. So when there is no change point, gave a value of $-\infty$ which made the single regimen model automatically win over any other change point configuration. Because of this, this the single regimen had to be explicitly excluded. Now with $\ln (j^* + 1)$ we can naturally incorporate this case. This means that the single regimen model can also be incorporated and compared against any other one models with multiple change points.

Let us notice that for evaluating (7) we need to calculate $\hat{\phi }$ for a given value of the vector $\boldsymbol{\tau }^*$. This procedure for the MDL classifies as a bi-level optimization problem, where a problem is embedded within another. We refer to the embedded and outer problems as inner and outer optimization, respectively. In this case, the optimization for the MAP, $\hat{\phi }$, is the inner problem and the MDL approach corresponds to the outer optimization problem. For a more mathematical description of this kind of problem, the reader can refer to [8].

It is worth noting that the discrete nature of the location and number of change points makes this optimization problem harder to solve using continuous techniques such as gradient descent or the Newton Method, and in some cases, these techniques may be completely inapplicable. Consequently, a genetic algorithm proves to be a valuable tool for effectively exploring the parametric space.

4 Genetic Algorithm Details

The genetic algorithm is one of the so-called bio-inspired optimization algorithms based on evolution theory that aims to find the optimal value of a function. In our case, to identify the change point and parameters that better describe the data we use, we minimize (7).

The basic elements and tasks are done on the proposed genetic algorithm are:

• Individual. We codify each individual as a logical vector of the length of the observed times. “True” means that the corresponding time is a change point, and “False”, otherwise. Though the beginning and end of the scope of time are not properly change points, the coding should start and finish with “True” to define at least one regimen. The algorithm in [14] is considered to directly enlist the proposed ordered times as change points, but this new individual encoding is more convenient in terms of memory space and genetic operators.

• The scope of time. We consider the data that we want to estimate its change points as equidistant and discrete observations for exceedances in equal and non-overlapping units of time. Then the scope of time is equal to the length of data observations.

• Parameter estimation. Typical genetic algorithms do not include this step. Once an individual is defined, the change points are given and (6) can be optimized to find the MAP. The optimization can be done using any preferred method being Nelder-Mead our selected choice. The values for the parameters are part of the coding of an individual and are attached to the logical vector once they are estimated.

• A population. Consists of a fixed number of individuals and remains constant for different generations. This number is denoted by n.

• Fitness function. Once the parameter estimation is done, we can compute the MDL (7). This plays the role of the fitness function that induces a ranking for the individuals a generation. Based on this ranking, for each generation, we order the individuals to have an increasing ranking.

• Individual Generator. The first generation is generated with random individuals. Each logical value in each individual is assigned the same distribution where “True” is drawn as the “Success” in a distribution Bernoulli($\alpha =0.06$). In consequence, the number of change points in each individual has a binomial distribution with an average of six percent.

• Parents selection. In genetic algorithms, reproduction is simulated to generate new individuals. For this task, a pair of parents are selected with replacement with a weighted probability according to their rank. That is if i is the rank of i-th individual in the current population, it is selected with probability $i/ \sum _{j=1}^n j$.

• Crossover operator. The child will inherit all the change points from both parents. Then we keep each of these change points with probability 0.5.

• Corrector operator. In practice, it is inadequate to consider change points to be right next to each other. This operator prevents this from happening. In this scenario, one of the consecutive change points is randomly discarded. This excludes the first and last elements in the individual that must remain “True”.

• Mutation operator. Each of the new individuals is submitted to the mutation operator, where each change points is assigned a value of $-1,0$ or 1 with probabilities 0.4, 0.3 and 0.3 respectively. Then, the change points are modified accordingly by moving them one place to the left if the $-1$ value was assigned, unchanged if the 0 value is selected, and one place to the right if the 1 value is selected. This modification excludes the first and last elements of each individual.

Evolutionary algorithms start by setting an initial population of individuals. Since its selection involves some randomness, in an early stage, these individuals have a huge spread on the feasible space (see example in Fig. 1a) with respect to the best individual (red dot). This spreading is useful as it promotes the exploration of the search space. However, as generations pass, this spreading reduces considerably (Fig. 1b). While the typical genetic algorithm relies on a fixed number of iterations, an alternative is proposed that takes advantage of this behavior.

Fig. 1.

Individuals in $\mathbb {R}^2$ at different generations of the genetic algorithm (Color figure online)

We define the Average Generational Spread (AGS) as a measure of the dispersion of individuals in a generation. It is formally defined as:

$$\begin{aligned} \text{ AGS }(k) = \frac{1}{n} \sum _{i=1}^n \Vert \boldsymbol{x}^{(k)}_i -\boldsymbol{x}^{*(k)} \Vert ^2 \end{aligned}$$

(9)

where $\boldsymbol{x}^{*(k)}$ is the individual with the best value according to the fitness function MDL in the k-th generation, and $\boldsymbol{x}^{(k)}_i$ is the i-th individual in k-th generation. The individual codified as a logical vector makes the AGS function be evaluated very quickly using bit operations.

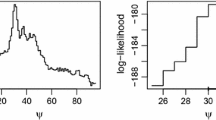
The AGS metric decreases rapidly in the first stages of the genetic algorithm and more slowly in the latter stages. See Fig. 2. To exploit this phenomenon, we propose using linear regression for the AGS values and the last K generations, where K is a fixed number. The idea is to determine an approximate value for the AGS slope $\psi$ for these last K generations. As a linear model is adjusted via linear regression, it can be determined, with a given significance, if there is evidence that the slope is still decreasing.

Fig. 2.

AGS value through generations.

Fig. 3.

Simulated Non-Homogeneous Poisson Process.

It can be seen in Fig. 2, that the values for the AGS have some noise due to the randomness induced by the genetic algorithm. For this reason, a statistical test is ideal for the task. Even more, as AGS is defined as an average, this suggests that it will tend to have a normal distribution. A classical t-test is used to evaluate the null hypothesis $H_0: \psi \le 0$ versus $H_1: \psi > 0$. If we reject $H_0$ we proceed to obtain the next K generations, and we stop otherwise.

Algorithms 1 and 2 present the overall proposed method.

5 Simulated Experiment

We evaluated the proposed algorithm using simulated data for which we know the number and location of its change points.

We generated a non-homogeneous Poisson process that simulates the cumulative counts of events with change points on times 299 and 699 with a scope of time of 1000. In contrast with some popular time series, the simulated times between counting increments are not equally distributed, which is one of the difficulties that our algorithm has to handle.

Figure 3 shows the simulated data. On the x-axis the time at which an event occurred and on the y-axis the cumulative counting process of these. It is shown in blue, orange, and green the three regimens induced by the change points. All three regimens are simulated with a Weibull rate function with parameters $[\alpha ,\beta ]$ equal to [0.4, 0.1], [0.8, 1.0], and [0.4, 0.1] for each regimen, respectively.

Now, to compute the MDL, and more precisely, the posterior density, we require to define the prior for the parameters involved. To do this we consider $\alpha \sim \text {Gamma}(1,2)$ and $\beta \sim \text {Gamma}(3,1.2)$, and an initial guess for parameter estimation we use $\alpha =0.1$ and $\beta =0.5$ for each regimen.

To assess the algorithm stability we ran it 100 times setting $K=10$ and a significance level of 0.05. This allows us to see if it is able to produce results that are consistently close to the true values.

We recorded the fitted number of change points, their location, and the number of generations spent to produce the output.

As for the number of change points, the algorithm was able to identify the true number of change points every single time. Regarding their positions, Figs. 4a and 4b show the histograms for the fitted times for the first and second change points. Both reported values are centered around the true values (lines in red). Mean values and variances are 295.01, 43.65 for the first change point, and 706.82, 151.11 for the second change point. Figure 4c depicts both histograms and makes evident how consistent the produced fitted values are in the 100 algorithm executions, as they present a very low deviation from the true values.

Fig. 4.

Histogram for the first and second reported change points. (Color figure online)

Regarding the algorithm efficiency, we plot the histograms for the number of generations before stopping. The algorithm was allowed to run a maximum of 100 generations, however, as we can see in Fig. 5a, most of the time it stopped before reaching 100 generations, and an important number of times it stopped close to the 20th generation.

Fig. 5.

Resulting number of generations spend and MDL histograms.

Figure 5b shows the histogram of the MDL values reported for the best individual in each of the 100 executions (between 332 and 346). With a red line, we mark the MDL value for an individual having the real values for the change points. It can be observed that our algorithm, achieves acceptable MDL values that are equal or lower than the MDL value at the real change points.

5.1 Comparison with Other Algorithms

The comparison of our method has been done with other four algorithms: (1) MDL2023, (2)Changepoint, (3) Prophet and (4) bcp.

MDL2023 is the version described in [14] and uses the same parameters (maximum number of generations, prior distribution, likelihood function, population size) as in our method. Changepoint, is a method that comes from the library changepoint in R, [10]. This library adjusts a Gaussian distribution to each regimen and, using a probability test determines the location of change points. For doing the fitting there are three options, (a) to detect a change in the mean, (b) to detect a change in variance, and (c) to detect a change in mean and variance. We report the results for these three options. Prophet corresponds to Facebook’s prophet algorithm, which is available for both Python and R, [15]. This method decomposes time series into three components

$$\begin{aligned} y(t) = g(t) + s(t) + h(t) + \varepsilon , \end{aligned}$$

(10)

with g(t) as the trend component, s(t) as the seasonal component, and h(t) as a special day component that considers events, like Easters, that occur every year, but not on the same day. The term $\varepsilon$ is an error with distribution $N(0,\sigma ^2)$. More features about the algorithm are detailed in [15].

Prophet is mainly focused on forecasting and the user can specify the known change points. However, when the change points information is not provided, it runs an algorithm to detect them. We considered four different options for change point detection, the first one runs the default settings. This suggests 25 change points and then uses the trend parameters to decide if these change points are significant or not. For the second option, the number of change points to be detected is given, but we do not specify their position. For this case, we select a number of 500 change points evenly distributed during the observation period. The algorithm establishes which ones are significant. For the fourth option, we set the threshold to a high value to keep more significant change points.

Finally, the fourth competing algorithm is Bayesian Change point, (bcp), [6]. This method is implemented in an R library that fits a Gaussian likelihood to data and assigns a prior density to the location of change points by assuming that whether a time is a change point or not depends on a subjacent Markov process. The output is a list of probabilities for each time to be a change point so we have to give a threshold to discriminate what we consider to be a change point.

We use the previous simulated NHPP data, depicted in Fig. 3, as the input for all the methods and we compare the results in terms of the number and location of the produced change points. The first algorithm, MDL2023, does not have a stopping criterion so the best individual at the last generation is reported.

For comparing the performance of MDL2023 and our proposed genetic algorithms, we ran each algorithm a hundred times. The reason to consider this is that the algorithms can return different results: number of change points and their respective locations. After that, we use all returned change points, for each method, to estimate their density. In a good identification scenario, we would expect a density with values mainly distributed around 299 and 699 (the true change points) and if the methods were similar we expected to have same density high around these values. With this density, we intend to visualize in a single plot, both fitting criteria (number and position) but we can also compare each of the method’s consistency.

Figure 6a shows the density obtained from MDL2023. This method frequently returned more change points than two, and their positions are pretty dispersed. Figure 6b shows the estimated density returned by our algorithm which is much more stable and consistently close to the real position values.

Fig. 6.

Density of change point reported.

As the algorithms Changepoint, Prophet and bcp provide only one possible output, we only required to run them once to evaluate its results, however, some options were explored to compare their performance against our method.

To apply Changepoint, we detrend the series by taking the first-order differences. Its first option (mean) did not report any change point at all. The second option (variance) detected only the change point at 699 which is the true position for one change point. The third option (mean and variance) returns a change point in 816 when the true position of the second change point is 699.

Prophet tends to return many more change points. The first option considered (default parameter values with 25 initial change points) 21 were returned (Fig. 7a). From this 21 there are a pair that are close to the real values of 299 and 699. For the second option, we specify two change points but they are not even close to their real position (Fig. 7b). For the third option, a total of 175 change points are returned (Fig. 7c). By default, the threshold parameter is set to 0.01. In the fourth option, we set again 500 change points, but a threshold of 0.15. The number of change points is reduced to sixteen, but only the value of 699 is caught between the reported change points (Fig. 7d).

For the case of bcp, the method reports 185 change points when setting a threshold of 0.9 for the probability of a time to be a change point.

Fig. 7.

Resulting change points with Prophet using different parameter values: Number of change points (NumCP) and Threshold value (Thr).

5.2 Conclusions and Future Work

One of the important features of the presented algorithm is that it can be used for observations that are similar to NHPP with Weibull rates. This proposal can be extended to other important types of parametric NHPP models, that share the attributes of not having increments that are identically distributed. Our method shows to be capable to identify the correct number of change points and provide good estimates for the change points positions.

On the other hand, the proposed stopping criterion allows the method to be highly efficient without sacrificing its precision. Compared to other competing methods, the results based on the simulated data show that our proposal can be very efficient, consistent, and can closely detect true change points (number and location).

Though the algorithm is giving good results, there still are many features that can be improved.

• 1. Starting point for parameter estimation. We used the same starting point for each individual to be optimized, however, the estimated parameters for the parents could provide a better initial estimate for the parameters of the child.

• 2. Hyper-parameters for the prior distribution. Justifying the parameters of prior distributions is always something to have in mind as they could lead to bias in the estimation. This usually is proposed using previous information, but a cross-validation technique could be applied.

• 3. Other penalization terms. Current penalization comes from [12] and information theory. The penalization used in this paper has made a little upgrade, but this can be improved by penalizing too short or too long regimes or promoting the exploration of other specific and desired properties of the data.

• 4. Prior distribution for $\boldsymbol{\tau }$. MDL can be interpreted from a Bayesian perspective as to give a prior distribution to $\boldsymbol{\tau }$. MDL could be modified using another criterion rather than information theory to give a more informed penalization term.