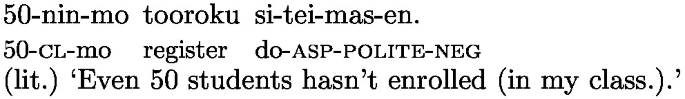Abstract
This paper offers a granularity-based account of the fact that round and non-round numbers may exhibit polarity effects when they are appended by even-type focus particles. The key observation is that non-round numbers appended by mo ‘even’ in Japanese cannot be in the scope of negation, while round numbers exhibit no restriction in scopal relation. Adopting the scope theory of mo and a theory of granularity ([6, 10]), we propose that an asymmetric entailment relation holds between propositions with a non-round and a round number and this entailment relation invites a proposition with a coarser granularity into the set of alternatives in computing the scalar presupposition of mo. Given that the scalar presupposition of mo with numerals is only sensitive to asymmetric entailment, we argue that the availability of asymmetric entailment from the prejacent to this additional alternative proposition is responsible for the polarity effects. We also discuss the related issues such as polarity effects observed in explicit approximators (e.g. about, approximately) and numerals with the contrastive topic marker wa.
We would like to express our gratitude to Stephanie Solt and anonymous reviewers of LENLS 19 for their invaluable comments on an earlier version of the paper. This work is supported by JSPS Grant-in-Aid 21K00525.
Access provided by Autonomous University of Puebla. Download conference paper PDF
Similar content being viewed by others
Keywords
1 Introduction
The recent literature on the polarity phenomena has revealed that vagueness and granularity have an impact on the polarity effect (e.g., [14] on approximators such as approximately and about, [1] on some NP and minimizers). This work is yet another contribution to this trend, reporting an unnoticed contrast between round and non-round numbers when associated with focus particles in Japanese. Our analysis predicts that this phenomenon is sensitive to what granularity is assumed in the context and to whether non-round and round numbers are in competition in the relevant context.
2 Data
It has been acknowledged that mo ‘even’ in Japanese invites different implications when it appears in positive or negative sentences, just like its counterpart in English. The positive version of (1a), for example, implies that Question 2 is hard, while with the negative version of (1a), Q2 is understood to be easy. Footnote 1

When mo is appended to numerals, as in (2a)–(2b), the implications are about how large the interlocutors consider them to be. The positive sentence in (2a) denotes a situation where John solved five problems, and implicates that ‘5’ is considered to be large.

(2b) is ambiguous: in one reading, it is true in a context where the number of problems John solved does not reach 5 (=(3a)), while in the other reading, it becomes true in a context where the number of problems John didn’t solve is five (=(3b)). These readings are associated with different implications: in Context A, ‘5’ is understood to be small, while in Context B, the same number is considered to be large. We call these two readings small and large number readings, respectively.Footnote 2

Even in English behaves differently from its Japanese counterpart in negative sentences. It induces a small-number reading (=Context A), and the large-number reading is very hard to get, if not impossible.Footnote 3

We observe that this ambiguity mysteriously disappears when we use a different number. The key observation here is that the small-number readings available for (2b) and (4) become mysteriously unavailable when the number included is a non-round one, such as 48, while the positive sentence does not exhibit any contrast between 50 and 48, as shown in (5a)–(5b)(see [3]).Footnote 4

This judgment is replicated in English even, in which even with numbers in negative sentences only has a small number reading.

Another interesting aspect of this phenomenon is context sensitivity: in (7), ‘25’ is judged to be weird, because in this case, the conspicuous unit of measure is 12. In other words, in this unit of measure, 25 cannot be a ‘round’ number.

The obvious question here is what makes ‘non-round’ numbers awkward in the negative context with mo. We propose that this contrast arises when the non-round numbers compete with round numbers in the satisfaction of the presupposition induced by mo.
3 The Scope Theory of Mo ‘Even’
We follow [7] and [8] in that Japanese mo is best analyzed in terms of the Scope Theory of even-items ([4]). In this theory, mo introduces a scalar presupposition without contributing to the assertive content, and its scalar meaning is defined by unlikeliness.Footnote 5

It has been argued that the hard/easy implications observed in (1a) are due to this scalar presupposition ([4]). Nakanishi [7] argues that the small and large readings also come from the scalarity of mo, with crucial assumptions that numeral expressions are interpreted to be one-sided, ‘at least n’, and that the unlikeliness is equated with asymmetric entailment, as in (9).Footnote 6

Under this setting, John solved n problems asymmetrically entails a proposition John solved m problems, where m < n.
The scope theory of mo espouses that mo moves to a propositional level at LF, even if it is appended to a numeral or a DP. This produces the following LFs for the sentences in (2a)–(2b):

The LF in (10a) satisfies the presupposition of mo when the set of alternative propositions, C, consists of the propositions that are entailed by the prejacent. This means that the numerals included in the alternative propositions (other than the prejacent) are lower than 5. Since the prejacent proposition includes the largest number among the propositions in C, the large-number reading results.

In (10b), mo scopes over negation, which in turn takes scope over the numeral. To satisfy the presupposition of mo, the alternatives in C should be the ones that have a smaller number than 5, since the negation flips the entailment. This leads to the small number reading.

The configuration in (10c) again results in a large number reading. Since the negation takes a narrower scope than the numeral, the following entailment relation holds: if there are five problems that John didn’t solve, it is true that there are four problems that John didn’t solve. This leads to the large-number reading.

It should be noted here that in the scope theory of even-items, these items have to take scope over negation to yield appropriate interpretations. In Japanese, this is independently motivated by the general property of focus particles, which take a wider scope than negation.Footnote 7 Take dake ‘only’, for example. In (14) below, the only interpretation possible is an interpretation where only takes a wider scope than negation.Footnote 8

The data that concerns us here is now understood in the following way: the contrast between the round and non-round numbers arises when mo takes a proposition in which negation takes scope over numerals (=(15b)).

This generalization is supported by the fact that the contrast is not observed when mo takes a narrower scope than other ‘negative’ operators. In Japanese, mo does not move across a clause boundary ([8]), which is evidenced by the lack of the ‘easy’ reading in (16). If mo takes a proposition within which a ‘negative’ operator does not take scope over a numeral, it is predicted that there will be no contrast between 50 and 48 observed. This prediction seems to be borne out, as shown in (17).


In the next section, we explain why the generalization in (15) holds, based on granularity.
4 Proposal
4.1 Granularity in Number
Before moving to our proposal, we first lay out how round and non-round numbers are treated in this paper.
We have described ‘50’ can be a round number, while ‘48’ is not. In other words, we understand ‘48’ as a precise number when we say ‘Taro solved 48 problems,’ while ‘50’ in ‘Taro solved 50 problems.’ can be understood to denote an exact number Taro solved or an approximate number he solved. Krifka [6] formulates this in terms of the Coarsest Scale Principle in (18): That ‘50’ is on the coarser and finer scales in (19) makes it possible to have an approximate interpretation.


We follow [10] and [14] in that granularity is formulated as a contextual parameter of interpretation. A granularity function,
 is a function that maps a number, n to the interval [n − 1/2 \(\times i\) \(\le \) n \(\le \) n \(+\) 1/2 \(\times i\) ], where i represents the granularity level. Under this formulation, for example, ‘50’ on the coarser scale in (19) denotes the interval from [45–55], and ‘48’ on the finer scale in (19) denotes the interval from [47.5-48.5].
is a function that maps a number, n to the interval [n − 1/2 \(\times i\) \(\le \) n \(\le \) n \(+\) 1/2 \(\times i\) ], where i represents the granularity level. Under this formulation, for example, ‘50’ on the coarser scale in (19) denotes the interval from [45–55], and ‘48’ on the finer scale in (19) denotes the interval from [47.5-48.5].

We can now define the relative coarseness of granularity functions, as in (21).
 is finer than
is finer than
 since the former returns a narrower interval when it is applied to a number than when the latter is applied to the same number.
since the former returns a narrower interval when it is applied to a number than when the latter is applied to the same number.

Under this interpretation of granularity, if there is a context where you can truthfully say (22a), then there should be a context where you can truthfully say (22b). This relation holds when the interval denoted by
 (48) falls within the one denoted by
(48) falls within the one denoted by
 (50).
(50).

The relation between these two is one of entailment: if (22a) is true in a context, then (22b) has to be true in another context. This notion of entailment is thus formulated as follows:

(23) is, in effect, the condition for rounding numbers. Thus ‘48’ can be rounded to ‘50’, but not vice versa.
4.2 Polarity Effects Explained
In the previous section, we made a crucial assumption that the unlikeliness of mo, when appended to numerals, is equated with asymmetric entailment. In other words, mo appended to numerals is sensitive to entailment relation between its possible alternatives. We propose that an alternative set C contains a proposition with a coarser granularity when it satisfies the relation in (23) with the prejacent. In simpler terms, when the numeral in the prejacent can be rounded to another numeral, then C has to include the proposition with the round number as one of the alternative propositions.
Let us now proceed to how this proposal accounts for our data. Consider first the affirmative cases. Since mo does not contribute to the assertive content, we will only consider whether the scalar presupposition is satisfied. (24a) has the prejacent proposition that may be truthfully denoted by a proposition with a round number. Thus the set of alternative propositions in (25b) has to include that proposition (=the underlined one), in addition to the propositions with the same granularity level. Since the prejacent ‘John solved
 problems.’ entails all the other propositions in C, the scalar presupposition of mo is satisfied.
problems.’ entails all the other propositions in C, the scalar presupposition of mo is satisfied.

(24b), in turn, does not include alternatives with different granularity levels, since the prejacent does not entail, say, ‘John solved
 problems.’ The computation of the scalar presupposition goes through as usual, with either of
problems.’ The computation of the scalar presupposition goes through as usual, with either of
 .
.

In the case of negative sentences, two LF are possible, (27b) and (27c).

Let us first consider the wider scope negation reading with ‘48’. Since ‘48’ is a number that conforms to the relation in (23), C has to include a proposition with a different granularity as its member (=the underlined one in (28b)). Since we espouse the ‘at least’ semantics of numerals, the prejacent does not entail ‘\(\lnot \) John solved
 problems.’ (see (29)). This leads to the unsatisfied presupposition, and thus the unacceptability results.
problems.’ (see (29)). This leads to the unsatisfied presupposition, and thus the unacceptability results.


With the numeral taking wider scope, as in (27c), the proposition ‘there are
 problems that John didn’t solve.’ has to be added to the set of alternatives, but this time it does not do any harm: Just like the affirmative case, ‘there are
problems that John didn’t solve.’ has to be added to the set of alternatives, but this time it does not do any harm: Just like the affirmative case, ‘there are
 problems that John didn’t solve’ entails ‘there are 50
problems that John didn’t solve’ entails ‘there are 50
 problems that John didn’t solve’. The scalar presupposition of mo is satisfied in this reading.
problems that John didn’t solve’. The scalar presupposition of mo is satisfied in this reading.
Our proposal that a proposition with a different granularity level is added to the set of alternatives when we compute the scalar presupposition of mo thus predicts the contrast between the round and non-round numbers we observed in Sect. 2.
4.3 Some Predictions
The current proposal is based on the idea that a numeral + mo sounds awkward when it can be rounded without making the sentence false. This reasoning leads to the prediction that if a numeral is not rounded to another one, then it does not exhibit awkwardness. This prediction is actually borne out, as shown in (30b). According to the definition in (23), ‘3’ cannot be rounded to any number with, say,
 :
:

Another consequence of the proposal is that if the context in question makes it easier to access a particular measure of the unit, the numerals that would not show a contrast in other contexts may exhibit a difference in acceptability. (7), repeated here as (31) below, is just the case: In (31), the conspicuous measure of the unit is 12, and thus 25 can be replaced by 24, without making the (affirmative) sentence false.

Putting a proposition with a different granularity level into a set of alternatives when the number can be rounded to another one thus explains apparently mysterious contrasts between round and non-round numbers in negative sentences.
5 Discussion
This section presents some issues that arise from our analysis.
5.1 Approximately N
Solt [14] observes that numerals modified by ‘approximators’ such as approximately, about, roughly avert negative contexts:

Japanese behaves in the same way, in that the reading where the modified numeral has a narrower scope than negation is not available in (33).

The possible scopal relation is confined to the one where negation takes a narrower scope when modified numerals appended by mo:

Our analysis does not seem to predict this distribution. Let us assume that the approximators restrict possible granularity functions to the coarsest possible in the given context (cf. [10, 13]). Since this does not require a proposition with a different granularity in its alternatives, the scalar presupposition of mo should be satisfied.


Solt [14] argues that the PPI-hood of numerals modified by approximators comes from the conversational principle in (37) ([5]) when they are in competition with bare numerals in their structural terms. Under her denotations of modified and bare numerals, these two may not be better than the other from the informational perspective, but the latter is definitely simpler in form and thus better in this respect. So if the speaker uses a proposition with a modified numeral, she/he implicates that an alternative proposition with a bare numeral cannot be asserted.

Suppose we understand that about 50 problems denotes the interval around (precisely) ‘50’. In that case, the negative sentence with the modified numeral causes a contradiction, while the affirmative does not cause any trouble: asserting that John didn’t solve [50-k, 50+k] problems implicates the speaker cannot assert that John didn’t solve 50 problems, which in turn means that John solved 50 problems.
We might thus explain the oddness of (34) with wide-scope negation reading by resorting to the PPI-hood of modified numerals.
5.2 Contrastive Topic Marker Wa and Numerals
Ijima ([3]) has made another observation that when a non-round number is appended by the contrast topic marker wa, the sentence becomes odd whether it is in an affirmative or negative context:

Let us first adopt a scalar analysis of wa ([11]). Sawada [11] claims that wa works as a mirror image of mo ‘even’, proposing the following semantics.

The scalar presupposition in (39b) requires that the prejacent p should be the most likely among the set of alternative propositions C (i.e., p is entailed by all the other alternatives in C.)
If we apply this denotation of wa to (38a), we will get the following results:

Just like the other examples with ‘48’, the alternative set includes a proposition with a different granularity (=the underlined one in (40d)), which is entailed by the prejacent ‘John solved 48-wa problems’. The scalar presupposition is not thus satisfied and the infelicity is predicted as desired.
Unfortunately, the same analysis cannot be extended to the negative sentence in (38b): we predict that the scalar presupposition of wa is satisfied in this case.

In the negative environment, the entailment relationship is reversed, and the underline proposition above entails the prejacent. Thus, the prejacent is the most likely in C, and the scalar presupposition is satisfied.
Let us now adopt a non-scalar analysis of wa ([2]). Hara ([2]) also proposes that wa introduces defindness condition without contributing to the assertion, which requires the existence of at least one stronger proposition than the assertion. Furthermore, this produces an uncertainty implicature where it is possible that the stronger proposition is false.

The application of this analysis to our case does not give us what we want: since there is at least one stronger alternative in C in (42c), say, John solved
 problems, this should not cause any problems, even if we have an alternative with different granularity.
problems, this should not cause any problems, even if we have an alternative with different granularity.

The same holds of the negation, and thus we cannot explain the distribution of ‘48’ with wa.
The above discussions indicate that unlike the cases with mo, the incompatibility of wa with non-round numbers is not due to the entailment relation between round and non-round numbers. Thus, we need a different, non-entailment-based analysis, and we speculate that the uncertainty implicature induced by wa is at odds with the fine granularity of non-round numbers. In (38a) and (38b), the speaker implicates that she or he does not have perfect knowledge about numbers greater/smaller than 48 but at the same time, she or he uses the non-round number, indicating that she or he has sufficient knowledge to choose the fine granularity scale. Given that the choice of the precise scale increases the speaker’s certainty, non-round numbers seem to be incompatible with the contrastive topic marker
 . However, we leave the detailed exposition of this analysis for future work.
. However, we leave the detailed exposition of this analysis for future work.
6 Conclusion
This paper has discussed an unfamiliar polarity effect observed with non-round and round numbers appended by mo and proposes that a proposition with a non-round number has to include a proposition with a number with a coarser granularity. It is important to note here that the contrast reported here is not confined to Japanese mo: as we noted above English exhibits the same contrast. This indicates that this phenomenon could be robust across languages, which we have to leave for future work. We hope that our work will contribute to the understanding of the roles of granularity in polarity effects, which has gained a lot of attention in recent literature.
Notes
- 1.
Mo has several usages as exemplified below. We will confine ourselves to the scalar usage with a similar meaning to ‘even’ in this paper. We do not make any specific assumption about the issue of whether these different usages come from a single source or not.
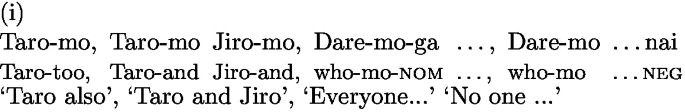
.
- 2.
- 3.
Nakanishi [8, 185] notes that the large-number reading is indeed not impossible in English, as shown in (i):
(i) Al, Bill and Conan always read everything they are assigned, but this time, they each had some books that they didn’t read. Al didn’t read
 book, Bill didn’t read
book, Bill didn’t read
 books and Conan ended up not even reading
books and Conan ended up not even reading
 .
. - 4.
- 5.
Even-items including mo may also introduce an additive presupposition (=(i)), but we will put this component aside in this paper.

.
- 6.
We do not claim that the unlikeliness of mo is always based on asymmetric entailment: this simply makes a wrong prediction. In (i), for example, it has to be the case that Taro came to the party is less expected than, say, Mary came to the party, which is not in entailment relation with the former.

What seems to be the case is that in the case of mo appended to numerals, the unlikeliness based on other than asymmetric entailment is not available.
- 7.
In footnote 2 we pointed out that (2b) has the third reading. The scopal relation involved in this reading should be [\(\lnot>\) mo > n]. This apparent inconsistency to what we claim here is resolved if we consider this reading to be actually a case of external negation. A piece of evidence for this view comes from the fact that this use requires a preceding discourse that refers to the number, as in (i).
(i) A: How many students are enrolled in your class this semester? 50 students have enrolled in mine.
B:
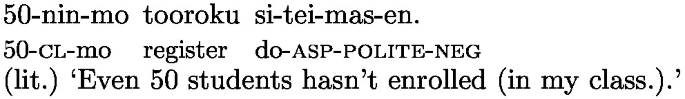
.
- 8.
See [12] for morpho-syntactic reasoning of this obligatory wide-scope reading of focus particles.
References
Goncharov, J., Wolf, L.: Deriving polarity from granularity. In: Proceedings of SALT, vol. 31, pp. 683–702 (2021)
Hara, Y.: Grammer of Knowledge Representation: Japanese Discourse Items at Interfaces. Ph.D. thesis, University of Delaware (2006)
Ijima, M.: Suuryooshi to wa to mo (quantifiers and wa and mo). In: Tsukishima Hiroshi sensei koki kinen kokugogaku ronshu (A Festschrift for Professor Hiroshi Tsukishima on his 70th birthday), pp. 1041–1062. Kyuuko shoin (1995)
Karttunen, L., Peters, S.: Conventional implicature. Syntax Semant. 11, 1–56 (1979)
Katzir, R.: Structurally-defined alternatives. Linguist. Philos. 30, 669–690 (2007)
Krifka, M.: Approximate interpretations of number words: a case for strategic communication. In: Hinrichs, E., Nerbonne, J. (eds.) Theory and evidence in semantics, pp. 109–132. CSLI Publications, Stanford (2009)
Nakanishi, K.: Even, only, and negative polarity in Japanese. In: Proceedings of SALT, vol. 16, pp. 138–155 (2006)
Nakanishi, K.: Scope of Even: A cross-linguistic perspective. In: Proceedings of NELS , vol. 38, pp. 179–192 (2009)
Nakanishi, K.: Focus particle ‘mo’ appended to numerals and negation (suushi toritate-no ‘mo’ to hitei). In: Kato, Y., Yoshimura, A., Imani, I. (eds.) Negation and Linguitic Theory (Hitei to Gengo Riron), pp. 260–284. Kaitakusha (2010)
Sauerland, U., Stateva, P.: Scalar vs. epistemic vagueness: evidence from approximators. In: Proceedings of SALT, vol. 17, pp. 228–245 (2007)
Sawada, O.: The Japanese contrastive Wa: a mirror image of EVEN. In: Proceedings of Berkeley Linguistic Society, vol. 34, pp. 281–292 (2008)
Shibata, Y.: Negative structure and object movement in Japanese. J. East Asian Linguis. 24(3), 217–269 (2015). https://doi.org/10.1007/s10831-014-9131-9
Solt, S.: An alternative theory of imprecision. In: Proceedings of SALT, vol. 24, pp. 514–533 (2014)
Solt, S.: Approximators as a case study of attenuating polarity items. In: Hucklebridge, S., Nelson, M. (eds.) Proceedings of NELS, vol. 48, pp. 91–104 (2018)
Author information
Authors and Affiliations
Corresponding author
Editor information
Editors and Affiliations
Rights and permissions
Copyright information
© 2023 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this paper
Cite this paper
Tanaka, E., Mizutani, K. (2023). Granularity in Number and Polarity Effects. In: Bekki, D., Mineshima, K., McCready, E. (eds) Logic and Engineering of Natural Language Semantics. LENLS 2022. Lecture Notes in Computer Science, vol 14213. Springer, Cham. https://doi.org/10.1007/978-3-031-43977-3_4
Download citation
DOI: https://doi.org/10.1007/978-3-031-43977-3_4
Published:
Publisher Name: Springer, Cham
Print ISBN: 978-3-031-43976-6
Online ISBN: 978-3-031-43977-3
eBook Packages: Computer ScienceComputer Science (R0)





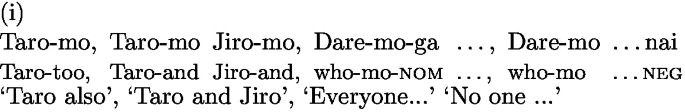
 book, Bill didn’t read
book, Bill didn’t read
 books and Conan ended up not even reading
books and Conan ended up not even reading
 .
.