Logic Operators and Quantifiers in Type-Theory of Algorithms

Abstract

In this work, I introduce the Type-Theory of Algorithms (TTA), which is an extension of Moschovakis Type-Theory of Algorithms and its reduction calculus, by adding logic operators and quantifiers. The formal language has two kinds of terms of formulae, for designating state-independent and state-dependent propositions and predications. The logic operators include conjunction, disjunction, conditional implication, and negation. I add state-dependent quantifiers, for enhancing the standard quantifiers of predicate logic. I provide an extended reduction calculus of the Type-Theory of Acyclic Algorithms, for reductions of terms to their canonical forms. The canonical forms of the terms provide the algorithmic semantics for computing the denotations.

1 Introduction

This paper is part of the author’s work on development of a new type-theory of the mathematical notion of algorithms, its concepts, and potentials for applications to advanced, computational technologies, with a focus on Computational Semantics and Syntax-Semantics-Semantics Interfaces for formal and natural languages.

For the initiation of this approach to mathematics of algorithms, see the original work on the formal languages of recursion (FLR) by Moschovakis [15,16,17]. The formal languages of recursion FLR are untyped systems. The typed version of this approach to algorithmic, acyclic computations was introduced, for the first time, by Moschovakis [18], with the type theory $\text {L}^{\lambda }_{\text {ar}}$. Type theory $\text {L}^{\lambda }_{r}$ covers full recursion and is an extension of type theory of acyclic recursion $\text {L}^{\lambda }_{\text {ar}}$.

For more recent developments of the language and theory of acyclic algorithms $\text {L}^{\lambda }_{\text {ar}}$, see, e.g., [6,7,8]. The work in [11] presents an algorithmic $\eta$-rule with the induced $\eta$-reduction acting on canonical terms in $\text {L}^{\lambda }_{\text {ar}}$, as a special case of ($\gamma ^*$). The algorithmic expressiveness of $\text {L}^{\lambda }_{\text {ar}}$ has been demonstrated by its applications to computational semantics of natural language. Algorithmic semantics of quantifier scope ambiguities and underspecification is presented in [3]. Computational grammar of natural language that coveres syntax-semantics interfaces is presented in [5]. The work in [8] is on fundamental notions of algorithmic binding of argument slots of relations and functions, across assignments in recursion terms. It models functional capacities of neural receptors for neuroscience of language. A generalised restrictor operator is introduced in $\text {L}^{\lambda }_{\text {ar}}$ for restricted, parametric algorithms, e.g., in semantics of definite descriptors, by [9], which is extended in a forthcoming publication. Currying order and limited, restricted algorithmic $\beta$-conversion in $\text {L}^{\lambda }_{\text {ar}}$ are presented by [10].

In this paper, I extend the formal language, reduction calculus, and semantics of $\text {L}^{\lambda }_{\text {ar}}$ and $\text {L}^{\lambda }_{r}$, by adding logic operators and logic quantifiers, with two versions of truth values: pure truth values and state-dependent ones. I introduce the logic operators of conjunction, disjunction, implication, and negation in the formal languages of $\text {L}^{\lambda }_{\text {ar}}$ and $\text {L}^{\lambda }_{r}$ by categorematic, logic constants, which have the benefits of sharing various properties and reduction rules with non-logic constants, while maintaining their logical characteristics.

In Sect. 2, I introduce the extended type-theory $\text {L}^{\lambda }_{\text {ar}}$ and $\text {L}^{\lambda }_{r}$ of acyclic algorithms, by its syntax and denotational semantics. The focus of the rest of the paper is on the acyclic type-theory $\text {L}^{\lambda }_{\text {ar}}$. In Sect. 3, I present the extended system of reduction rules and the induced $\gamma ^{*}$-reduction calculus of $\text {L}^{\lambda }_{\text {ar}}$. The additional reduction rule ($\gamma ^*$) greatly reduces the complexity of the terms, without affecting the denotational and algorithmic semantics of $\text {L}^{\lambda }_{\text {ar}}$, in any significant way. I provide the full, formal definition of the congruence relation between terms, which is part of the reduction system of both $\text {L}^{\lambda }_{\text {ar}}$ and $\text {L}^{\lambda }_{r}$. The reduction calculus of $\text {L}^{\lambda }_{\text {ar}}$ reduces each $\text {L}^{\lambda }_{\text {ar}}$ term to its canonical form. For every term A, its canonical form is unique modulo congruence. The canonical form of every proper $\text {L}^{\lambda }_{\text {ar}}$ term determines the algorithm for computing its denotation and saving the component values, including functions, in memory slots for reuse. Section 4 is on the algorithmic expressiveness of $\text {L}^{\lambda }_{\text {ar}}$. Theorem 2 proves that $\text {L}^{\lambda }_{\text {ar}}$ is a proper extension of Gallin $\textrm{TY}_2$, see Gallin [1]. There are $\text {L}^{\lambda }_{\text {ar}}$ recursion terms that are not algorithmically equivalent to any explicit, $\lambda$-calculus, i.e., $\textrm{TY}_2$ terms. In addition, such $\text {L}^{\lambda }_{\text {ar}}$ recursion terms, provide subtle semantic distinctions for expressions of natural language. The focus of Sect. 5 is on the semantic and algorithmic distinctions between coordinated predication and sentential conjunction. In Sect. 6, I overview some relations between let-expressions for $\lambda$-calculus and $\text {L}^{\lambda }_{\text {ar}}$ recursion terms. I give an explanation why the $\text {L}^{\lambda }_{\text {ar}}$ recursion terms are not algorithmically equivalent to $\lambda$-terms in $\text {L}^{\lambda }_{\text {ar}}$ representing let-expressions. I demonstrate the extended reduction calculus with reductions of terms to their canonical forms, which offer distinctive, algorithmic semantics of natural language expressions.

2 Introduction to Type-Theory of Acyclic Algorithms

Type-theory of algorithms (TTA), in each of its variants of full and acyclic recursion, $\text {L}^{\lambda }_{r}$ and $\text {L}^{\lambda }_{\text {ar}}$, respectively, is a computational system, which extends the standart, simply-typed $\lambda$-calculus in its syntax and semantics.

The basis for the formal languages of $\text {L}^{\lambda }_{r}$ and $\text {L}^{\lambda }_{\text {ar}}$, and their denotational and algorithmic semantics is a tuple $\text {B}^{\lambda }_{\text {r}}= \left\langle \textsf{TypeR}, \textsf{K}, \textsf{Vars}, {\textsf{TermR}}, {\textsf{RedR}}\right\rangle$, where:

• (1) $\textsf{TypeR}$ is the set of the rules that defines the set Types

• (2) $\textsf{K}=\textsf{Consts}$ is a set of constants (2a)

• (3) $\textsf{Vars}$ is a set of variables (2f) of two kinds, pure and recursion (2d)–(2e)

• (4) ${\textsf{TermR}}$ is the set of the rules for the terms of $\text {L}^{\lambda }_{r}$ and $\text {L}^{\lambda }_{\text {ar}}$, given in Definition 1

• (5) ${\textsf{RedR}}$ is the set of the reduction rules given in Sect. 3.2

The focus of this work is on the type-theory $\text {L}^{\lambda }_{\text {ar}}$ of acyclic algorithms (TTAA).

Notation 1

We shall use the following meta-symbols (1)–(2):

• (1) “ $\equiv$” is used for notational abbreviations and definitions, i.e., for literal, syntactic identities between expressions. The equality sign “=” is for the identity relation between objects of $\text {L}^{\lambda }_{\text {ar}}$ ($\text {L}^{\lambda }_{r}$)

• (2) “ $\mathrel {\mathop :}\equiv$” is for the replacement, i.e., substitution operation, in syntactic constructions, and sometimes for definitional constructions

2.1 Syntax

The set $\textsf{Types}$ of $\text {L}^{\lambda }_{\text {ar}}$ is defined recursively, e.g., in Backus-Naur Form (BNF):

The type $\textsf{e}$ is for basic entities and $\text {L}^{\lambda }_{\text {ar}}$ terms denoting such entities, e.g., for animals, people, etc., animate or inanimate objects. The type $\textsf{s}$ is for states that carry context information, e.g., possible worlds, time and space locations, speakers, listeners, etc. The denotations of some expressions of natural language, e.g., proper names and other noun phrases (NPs), can be rendered (translated) to $\text {L}^{\lambda }_{\text {ar}}$ terms of type $(\textsf{s} \rightarrow \textsf{e})$. The type $\textsf{t}$ is for truth values. For any $\tau _{1}, \tau _2 \in \textsf{Types}$, the type $(\tau _{1} \rightarrow \tau _2)$ is for functions from objects of type $\tau _{1}$ to objects of type $\tau _2$, and for $\text {L}^{\lambda }_{\text {ar}}$ terms denoting such functions. We shall use the following abbreviations:

$$\begin{aligned} \widetilde{\sigma } &\equiv (\textsf{s} \rightarrow \sigma ), \quad \text {for state-dependent objects of type }\widetilde{\sigma } \end{aligned}$$

(1a)

$$\begin{aligned} \widetilde{\textsf{e}} &\equiv (\textsf{s} \rightarrow \textsf{e}), \quad \text {for state-dependent entities} \end{aligned}$$

(1b)

$$\begin{aligned} \widetilde{\textsf{t}} & \equiv (\textsf{s} \rightarrow \textsf{t}), \quad \text {for state-dependent truth values}\end{aligned}$$

(1c)

$$\begin{aligned} (\overrightarrow{\tau } \rightarrow \sigma ) &\equiv (\tau _{1} \rightarrow \dots \rightarrow (\tau _{n} \rightarrow \sigma )) \in \textsf{Types}{} (n \ge 1) \nonumber \\ & \text {currying coding, for } \sigma , \tau _i \in \textsf{Types}, \ i = 1, \dots , n \end{aligned}$$

(1d)

Typed Vocabulary of $\text {L}^{\lambda }_{\text {ar}}$: For every $\sigma \in \textsf{Types}$, $\text {L}^{\lambda }_{\text {ar}}$ has denumerable sets of constants, and two kinds of infinite, denumerable sets of pure and recursion variables, all in pairwise different sets:

$$\begin{aligned} & \textsf{K}_{\sigma } = \textsf{Consts}_{\sigma } = \{\textsf{c}^{\sigma }_{0}, \textsf{c}^{\sigma }_{1}, \dots \}; \qquad \qquad \textsf{K} =\textsf{Consts}= {\textstyle \bigcup _{\tau \in \textsf{Types}} K_{\tau }} \end{aligned}$$

(2a)

$$\begin{aligned} & \wedge , \vee , \rightarrow {} \in \textsf{Consts}_{(\tau \rightarrow (\tau \rightarrow \tau ))}, \ \tau \in \{\, \textsf{t}, \, \widetilde{\textsf{t}}\,\} \qquad \qquad \qquad \text {(logical constants)} \end{aligned}$$

(2b)

$$\begin{aligned} & \lnot \in \textsf{Consts}_{(\tau \rightarrow \tau )}, \ \tau \in \{\, \textsf{t}, \, \widetilde{\textsf{t}}\,\} \qquad \qquad \qquad \text {(logical constant for negation)} \end{aligned}$$

(2c)

$$\begin{aligned} & \textsf{PureV}_{\sigma }= \{v^{\sigma }_{0}, v^{\sigma }_{1}, \dots \}; \qquad \qquad \qquad \ \ \textsf{PureV}= {\textstyle \bigcup _{\tau \in \textsf{Types}} \textsf{PureV}_{\tau } } \end{aligned}$$

(2d)

$$\begin{aligned} & \textsf{RecV}_{\sigma } = \textsf{MemoryV}_{\sigma } = \{p^{\sigma }_{0}, p^{\sigma }_1, \dots \}; \quad \, {\textstyle \textsf{RecV}= \bigcup _{\tau \in \textsf{Types}} \textsf{RecV}_{\tau } } \end{aligned}$$

(2e)

$$\begin{aligned} & \textsf{PureV}_{\sigma } \cap {} \textsf{RecV}_{\sigma } = \varnothing ; \quad \textsf{Vars}_{\sigma } = \textsf{PureV}_{\sigma } \cup \textsf{RecV}_{\sigma }; \quad \textsf{Vars}= {\textstyle \bigcup _{\tau \in \textsf{Types}} \textsf{Vars}_{\sigma }} \end{aligned}$$

(2f)

Pure variables $\textsf{PureV}$ are used for $\lambda$-abstraction and quantification. On the other hand, the recursion variables, which are called also memory variables, memory locations (slots, cells), or location variables, play a special role in algorithmic computations, for saving information. Values, which can be obtained either directly by immediate, variable valuations, or by algorithmic computations, via recursion or iteration, can be saved, i.e., memorised, in typed memory locations, i.e., in memory variables, of the set $\textsf{RecV}$, by assignments. Sets of assignments can determine mutually recursive or iterative computations.

I shall use mixed notations for type assignments, $A : \tau$ and $A^{\tau }$, to express that a term A or an object A is of type $\tau$.

In Definition 1, I introduce the logical constants as categorematic constants for conjunction, disjunction, implication, $\wedge , \vee , \rightarrow {} \in \textsf{Consts}_{(\tau \rightarrow (\tau \rightarrow \tau ))}$, and negation, $\lnot \in \textsf{Consts}_{(\tau \rightarrow \tau )}$, in two variants of truth values $\tau \in \{\, \textsf{t}, \, \widetilde{\textsf{t}}\,\}$.

Definition 1

${\textsf{Terms}}= {\textsf{Terms}}(\text {L}^{\lambda }_{\text {ar}}) = \bigcup _{\tau \in \textsf{Types}} {\textsf{Terms}}_{\tau }$ is the set of the terms of $\text {L}^{\lambda }_{\text {ar}}$, where, for each $\tau \in \textsf{Types}$, ${\textsf{Terms}}_{\tau }$ is the set of the terms of type $\tau$, which are defined recursively by the rules ${\textsf{TermR}}$ in (3a)–(3g), in a typed style of Backus-Naur Form (TBNF):

$$\begin{aligned} A &\mathrel {\mathop :}\equiv {} \textsf{c}^{\tau } : \tau \mid x^{\tau } : \tau \qquad \qquad \qquad \qquad \qquad \qquad (\text {constants and variables}) \end{aligned}$$

(3a)

$$\begin{aligned} & \mid B^{(\sigma \rightarrow \tau )}(C^{\sigma }) : \tau \qquad \qquad \qquad \qquad \qquad \qquad \qquad \, (\text {application terms}) \end{aligned}$$

(3b)

$$\begin{aligned} & \mid \lambda (v^{\sigma })(B^{\tau }) : (\sigma \rightarrow \tau ) \qquad \qquad \qquad \qquad \qquad \quad \, (\lambda \text {-abstraction terms}) \end{aligned}$$

(3c)

$$\begin{aligned} & \mid A_{0}^{\sigma _{0}} \mathrel {\textsf{where}} \{ \, p_{1}^{\sigma _{1}} \mathrel {\mathop :}=A_{1}^{\sigma _{1}}, \dots , p_{n}^{\sigma _{n}} \mathrel {\mathop :}=A_{n}^{\sigma _{n}} \, \} : \sigma _{0} \qquad \, (\text {recursion terms}) \end{aligned}$$

(3d)

$$\begin{aligned} & \begin{aligned} & \mid \wedge (A^{\tau }_{2}) (A^{\tau }_{1}) : \tau \, \mid {} \vee (A^{\tau }_{2}) (A^{\tau }_{1}) : \tau \, \mid {} \rightarrow (A^{\tau }_{2}) (A^{\tau }_{1}) : \tau \\ & \ ( \text {conjunction} \ \ / \ \ \text {disjunction} \ \ / \ \ \text {implication terms}) \end{aligned} \end{aligned}$$

(3e)

$$\begin{aligned} &\mid \lnot {} (B^{\tau }) : \tau \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad (\text {negation terms}) \end{aligned}$$

(3f)

$$\begin{aligned} &\mid \forall (v^{\sigma }) (B^{\tau }) : \tau \, \mid {} \exists (v^{\sigma }) (B^{\tau }) : \tau \qquad \qquad \ (\text {pure, logic quantifier terms}) \end{aligned}$$

(3g)

given that

• (1) $\textsf{c} \in K_{\tau } = \textsf{Consts}_{\tau }$

• (2) $x^{\tau } \in \textsf{PureV}_{\tau } \cup \textsf{RecV}_{\tau }$ is a pure or memory (recursion) variable,

  $v^{\sigma } \in \textsf{PureV}_{\sigma }$ is a pure variable

• (3) $A^{\tau }_{1}, A^{\tau }_{2}, B, A_i^{\sigma _i} \in {\textsf{Terms}}$ ($i=0, \dots , n$) are terms of the respective types

• (4) In (3d), for $i = 1$, ..., n, $p_i \in \textsf{RecV}_{\sigma _i}$ are pairwise different recursion (memory) variables; $A_i^{\sigma _i} \in {\textsf{Terms}}_{\sigma _i}$ assigned to $p_i$ is of the same corresponding type; and the sequence of assignments $\{ \, p_{1}^{\sigma _{1}} \mathrel {\mathop :}=A_{1}^{\sigma _{1}}, \dots , p_{n}^{\sigma _{n}} \mathrel {\mathop :}=A_{n}^{\sigma _{n}} \, \}$ is acyclic, by satisfying the Acyclicity Constraint (AC) in Definition 2.

• (5) In (3e)–(3g), $\tau \in \{\, \textsf{t}, \, \widetilde{\textsf{t}}\,\}$ are for state-independent and state-dependent truth values, respectively

Definition 2

(Acyclicity Constraint (AC)). For any $A_{i} \in {\textsf{Terms}}_{\sigma _{i}}$ and pairwise different memory (recursion) variables $p_{i} \in \textsf{RecV}_{\sigma _{i}}$, $i \in \{\,1, \dots , n \,\}$, the sequence (4):

$$\begin{aligned} & \{ \, p_{1}^{\sigma _{1}} \mathrel {\mathop :}=A_{1}^{\sigma _{1}}, \dots , p_{n}^{\sigma _{n}} \mathrel {\mathop :}=A_{n}^{\sigma _{n}} \, \} \quad \text {(}n \ge 0\text {)} \end{aligned}$$

(4)

is an acyclic system of assignments iff there is a function $\textsf{rank}$

$$\begin{aligned} \begin{aligned} &\textsf{rank}: \{p_1, \ldots , p_n\} \rightarrow \mathbb {N},\text { such that,} \text { for all }p_i, p_j \in \{p_1, \ldots , p_n\}, \\ & \text {if }p_j\text { occurs freely in }A_i, \text {then } \textsf{rank}(p_j) < \textsf{rank}(p_i) \end{aligned} \end{aligned}$$

(AC)

Free and Bound Variables. The sets $\textsf{FreeVars}(A)$ and $\textsf{BoundVars}(A)$ of the free and bound variables of every term A are defined by structural induction on A, in the usual way, with the exception of the recursion terms. For the full definition, see [8]. For any given recursion term A of the form (3d), the constant $\mathrel {\textsf{where}}$ designates a binding operator, which binds all occurrences of $p_{1}, \dots , p_{n}$ in A:

$$\begin{aligned} \text {For } A &\equiv A_0 \mathrel {\textsf{where}}\{p_1 \mathrel {\mathop :}=A_1, \ldots , p_n \mathrel {\mathop :}=A_n\} \in {\textsf{Terms}}\end{aligned}$$

(5a)

$$\begin{aligned} \textsf{FreeV}(A) &= \cup _{i=0}^{n}{} (\textsf{FreeV}(A_{i})) - \lbrace \, p_{1}, \ldots , p_{n} \,\rbrace \end{aligned}$$

(5b)

$$\begin{aligned} \textsf{BoundV}(A) &= \cup _{i=0}^{n}{} (\textsf{BoundV}(A_{i})) \cup {} \lbrace \, p_{1}, \ldots , p_{n} \,\rbrace \end{aligned}$$

(5c)

The formal language of full recursion $\text {L}^{\lambda }_{r}$ is by Definition 1 without the Acyclicity Constraint (AC),

• (A) The terms A of the form (3d) are called recursion terms. The constant $\mathrel {\textsf{where}}$ designates a binding operator, which binds the recursion variables $p_1, \ldots , p_n$ in A. Its entire scope is A called $\mathrel {\textsf{where}}$-scope or its local recursion scope. The sub-terms $A_{i}$, $i = 0$, ..., n, are the parts of A and $A_{0}$ is its head part

• (B) We say that a term A is explicit iff the constant $\mathrel {\textsf{where}}$ does not occur in it

• (C) A is a $\lambda$-calculus term, i.e., a term of Gallin $\textrm{TY}_2$, iff it is explicit and no recursion variable occurs in it

Definition 3

(Free Occurrences and Replacement Operation). Assume that $A, C \in {\textsf{Terms}}$, $X \in \textsf{PureV}\cup \textsf{RecV}$ are such that, for some type $\tau \in \textsf{Types}$, $X, C : \tau$.

• (1) An occurrence of X in A is free (in A) if and only if it is not in the scope of any binding operator (e.g., $\xi \in \{\, \lambda , \exists , \forall \,\}$ and $\mathrel {\textsf{where}}$) that binds X

• (2) The result of the simultaneous replacement of all free (unless otherwise stated) occurrences of X with C in A is denoted by $A\lbrace \, X \mathrel {\mathop :}\equiv C \,\rbrace$

• (3) The replacement $A\lbrace \, X \mathrel {\mathop :}\equiv C \,\rbrace$ of X with C in A is free if and only if no free occurrence of X in A is in the scope of any operator that binds some variable having free occurrences in C: i.e., no variable that is free in C becomes bound in $A\lbrace \, X \mathrel {\mathop :}\equiv C \,\rbrace$. We also say that C is free for (replacing) X in A.

Notation 2

Often, we do not write the type assignments in the term expressions.

Sometimes, we shall use different kinds of or extra parentheses, or omit such. Application is associative to the left, $\lambda$-abstraction and quantifiers to the right.

In addition, we shall use abbreviations for sequences, e.g. ($n \ge 0$):

$$\begin{aligned} \overrightarrow{p} \mathrel {\mathop :}=\overrightarrow{A} &\equiv {} p_{1} \mathrel {\mathop :}=A_{1}, \ \dots , \ p_{n} \mathrel {\mathop :}=A_{n} \quad (n \ge 0) \end{aligned}$$

(6a)

$$\begin{aligned} H(\overrightarrow{A}) &\equiv {} H(A_1) \dots (A_n) \equiv {} ( \dots H (A_1) \dots ) (A_n) \qquad \text {(left-association)} \end{aligned}$$

(6b)

$$\begin{aligned} \xi {} (\overrightarrow{v} ) (A) &\equiv {} \xi (v_{1}) \dots \xi (v_{n}) (A) \equiv {} \xi (v_{1}) \bigl [ \ldots \bigl [ \xi (v_{n}) \bigl ( A \bigr ) \bigr ] \bigr ] \ \text {(right-association) }\nonumber \\ & \xi \in \{\, \lambda , \exists , \forall \,\} \quad (n \ge 0) \end{aligned}$$

(6c)

$$\begin{aligned} &\begin{aligned} \overrightarrow{\xi (v)} (A) & \equiv {} \xi _{1} (v_{1}) \dots \xi _{n} (v_{n}) (A) \equiv {} \xi _{1} (v_{1}) \bigl [ \ldots \bigl [ \xi _{n} (v_{n}) \bigl ( A \bigr ) \bigr ] \bigr ], \\ & \xi _{i} \in \{\, \lambda , \exists , \forall \,\}, \, i \in \{ 1, \dots , n \} \quad (n \ge 0) \end{aligned} \end{aligned}$$

(6d)

$$\begin{aligned} \textsf{lgh}(\overrightarrow{X}) & = \textsf{lgh}((X_1) \dots (X_n)) = n, \quad \, \textsf{lgh}(\xi {} (\overrightarrow{v} ) ) = n, \quad \, \textsf{lgh}(\overrightarrow{\xi (v)}) = n \end{aligned}$$

(6e)

2.2 Overview of Algorithmic Semantics in $\text {L}^{\lambda }_{\text {ar}}$ ($\text {L}^{\lambda }_{r}$)

The syntax-semantics interface in $\text {L}^{\lambda }_{\text {ar}}$ ($\text {L}^{\lambda }_{r}$) provides the interrelations between denotational and algorithmic semantics.

Definition 4

(Immediate and Pure Terms). The set of the immediate terms consists of all terms of the form (7), for $p \in \textsf{RecVars}$, $u_i, v_j, \in \textsf{PureVars}$ ($i = 1, \dots , n$, $j= 1, \dots , m$, $m,n \ge 0$), $V \in \textsf{Vars}$:

$$\begin{aligned} T \mathrel {\mathop :}\equiv {} & V \mid p(v_1) \dots (v_m) \mid \lambda (u_1) \dots \lambda (u_n) p(v_1) \dots (v_m), \quad \text {for }m,n \ge 0 \end{aligned}$$

(7)

Every term A that is not immediate is proper.

The immediate terms $T \equiv \lambda (\overrightarrow{u} ) p (\overrightarrow{v} )$ have no algorithmic meanings. Their denotational value $\textsf{den}(T)(g)$ is given immediately, by the valuation functions g for $g( v_i)$, and abstracting away from the values $u_j$, for $\lambda$-bound pure variables $\lambda (\overrightarrow{u} ) p (\overrightarrow{v} )$.

For every proper, i.e., non-immediate, term A, there is an algorithm $\textsf{alg}(A)$ for computing $\textsf{den}(A)(g)$. The canonical form $\textsf{cf}_{\gamma ^*}(A)$ of a proper term A determines the algorithm for computing its denotational value $\textsf{den}(A)(g) = \textsf{den}(\textsf{cf}_{\gamma ^*}(A))(g)$ from the components $\textsf{den}(A_{i})(g)$ of $\textsf{cf}_{\gamma ^*}(A)$. See $\gamma ^*$-Canonical Form Theorem 1, and [6,7,8, 18].

• The type theories $\text {L}^{\lambda }_{\text {ar}}$ have effective reduction calculi, see Sect. 3: For every $A \in {\textsf{Terms}}$, there is a unique, up to congruence, canonical form $\textsf{cf}_{\gamma ^*}(A)$, which can be obtained from A, by a finite number of reductions:

  $$\begin{aligned} A \mathrel {\Rightarrow ^{*}_{\gamma ^*}}\textsf{cf}_{\gamma ^*}(A) \end{aligned}$$

  (8)

• For a given, fixed semantic structure $\mathfrak {A}$ and valuations G, for every algorithmically meaningful, i.e., proper, $A \in {\textsf{Terms}}_{\sigma }$, the algorithm $\textsf{alg}(A)$ for computing $\textsf{den}(A)$ is determined by $\textsf{cf}(A)$, so that:

  $$\begin{aligned} \textsf{den}(A)(g) &= \textsf{den}(\textsf{cf}(A))(g), \ \text {for }g \in G \end{aligned}$$

  (9)

Figure 1 depicts of the syntax-semantics relations between the syntax of Natural Language, their rendering to the terms $\text {L}^{\lambda }_{\text {ar}}$ and the corresponding algorithmic and denotational semantics.

Fig. 1.

Computational Syntax-Semantics Interface for Algorithmic Semantics of Natural Language via Compositional Rendering to $\text {L}^{\lambda }_{\text {ar}}$.

2.3 Denotational Semantics of $\text {L}^{\lambda }_{\text {ar}}$

Definition 5

A standard semantic structure of the formal language $\text {L}^{\lambda }_{\text {ar}}(K)$ is a tuple $\mathfrak {A}(K) = \langle \mathbb {T}, \mathrel {\mathcal {I}}(K) \rangle$, where $\mathbb {T}$ is a frame of sets (or classes) $\mathbb {T} = \{\, \mathbb {T}_{\sigma } \mid \sigma \in \textsf{Types}\,\}$, and the following conditions (S1)–(S3) are satisfied:

• (S1) sets of basic, typed semantic objects:

  • $\mathbb {T}_e \not = \varnothing$ is a nonempty set (class) of entities called individuals

  • $\mathbb {T}_t = \{\, 0, 1, er \,\} \subseteq \mathbb {T}_e$, $\mathbb {T}_t$ is called the set of the truth values

  • $\mathbb {T}_s \not = \varnothing$ is a nonempty set of objects called states

• (S2) $\mathbb {T}_{(\tau _1 \rightarrow \tau _2)} = \lbrace \, f \mid f : \mathbb {T}_{\tau _1} \rightarrow \mathbb {T}_{\tau _2} \,\rbrace$

• (S3) The interpretation function $\mathrel {\mathcal {I}}$, $\mathrel {\mathcal {I}}: K \rightarrow \bigcup \mathbb {T}$, is such that for every constant $\textsf{c} \in K_{\tau }$, $\mathrel {\mathcal {I}}(\textsf{c})=c$, for some $c \in \mathbb {T}_{\tau }$

Definition 6

Assume a given semantic structure $\mathfrak {A}$. The set $G^{\mathfrak {A}}$ of all variable valuations (assignments) in $\mathfrak {A}$ is (10a)–(10b):

$$\begin{aligned} G^{\mathfrak {A}} = \{\, g \mid {} &g : (\textsf{PureV}\cup \textsf{RecV}) \rightarrow \cup \mathbb {T}, \end{aligned}$$

(10a)

$$\begin{aligned} & \text {and } g(x) \in \mathbb {T}_{\tau }, \text { for all }\tau \in Type \text { and }x \in \textsf{PureV}_{\tau } \cup \textsf{RecV}_{\tau } \,\} \end{aligned}$$

(10b)

Definition 7

(Denotation Function). A denotation function $\textsf{den}^{\mathfrak {A}}$ of the semantic structure $\text {L}^{\lambda }_{\text {ar}}(K)$, $\textsf{den}^{\mathfrak {A}} : {\textsf{Terms}}\rightarrow (G \rightarrow \bigcup \mathbb {T})$, is defined by structural recursion, for all $g \in G$:

• (D1) Variables and constants:

  $$\begin{aligned} \textsf{den}^{\mathfrak {A}}(x)(g) &= g(x), \text { for }x \in \textsf{Vars}; \quad \textsf{den}^{\mathfrak {A}}(\textsf{c})(g) = \mathcal {I}(\textsf{c}), \text { for }c \in K \end{aligned}$$

  (11)

• (D2) Application:

  $$\begin{aligned} \textsf{den}^{\mathfrak {A}}(A(B))(g) = \textsf{den}^{\mathfrak {A}}(A)(g)(\textsf{den}^{\mathfrak {A}}(B)(g)) \end{aligned}$$

  (12)

• (D3) $\lambda$-abstraction: for all $x : \tau$, $B : \sigma$, $\textsf{den}^{\mathfrak {A}}(\lambda (x)(B))(g) : \mathbb {T}_{\tau } \rightarrow \mathbb {T}_{\sigma }$ is the function such that, for every $t \in \mathbb {T}_{\tau }$,

  $$\begin{aligned}{}[\textsf{den}^{\mathfrak {A}}(\lambda (x) (B))(g)] \bigl ( t \bigr ) = \textsf{den}^{\mathfrak {A}}(B)(g\{x \mathrel {\mathop :}=t\}) \end{aligned}$$

  (13)

• (D4) Recursion:

  $$\begin{aligned} &\textsf{den}^{\mathfrak {A}} (A_0 \mathrel {\textsf{where}}\{\, \overrightarrow{p} \mathrel {\mathop :}=\overrightarrow{A} \,\}) (g) = \textsf{den}^{\mathfrak {A}}(A_0)(g\lbrace \, \overrightarrow{p_{i}} \mathrel {\mathop :}=\overrightarrow{\overline{p}_{i}} \,\rbrace ) \end{aligned}$$

  (14)

  where $\overline{p}_i \in \mathbb {T}_{\tau _i}$ are computed by recursion on $\textsf{rank}(p_i)$, i.e., by (15):

  $$\begin{aligned} \begin{aligned} \overline{p}_i &= \textsf{den}^{\mathfrak {A}}(A_i)(g\lbrace \, p_{i,1} \mathrel {\mathop :}=\overline{p}_{i,1}, \ldots , p_{i,k_i} \mathrel {\mathop :}=\overline{p}_{i,k_i} \,\rbrace )\\ &\text {for all }p_{i,1}, \dots , p_{i,k_i},\text { such that } \textsf{rank}(p_{i,k}) < \textsf{rank}(p_i) \end{aligned} \end{aligned}$$

  (15)

  The denotation $\textsf{den}(A_{i})(g)$ may depend essentially on the values stored in $p_{j}$, for $\textsf{rank}(p_{j}) < \textsf{rank}(p_i)$.

• (D5) Here, for the denotations of the constants of the logic operators, we shall present the state dependent cases, including the erroneous truth values. The state-independent cases are simpler and straightforwardly similar.

  • (D5a) $\textsf{den}^{\mathfrak {A}} \bigl ( A_{1} \wedge A_{2} \bigr ) (g) : \mathbb {T}_{\textsf{s}} \rightarrow \mathbb {T}_{\textsf{t}}$ is the function such that, for every state $s \in \mathbb {T}_{\textsf{s}}$:

    $$\begin{aligned}{}[\textsf{den}^{\mathfrak {A}}( A_{1} \wedge A_{2}) (g)] (s)&=V \in \mathbb {T}_{\textsf{t}}, \ \text {where }V\text { is as in } (\text {17a})-(\text {17c}) \end{aligned}$$

    (16)

    

  • (D5b) $\textsf{den}^{\mathfrak {A}} \bigl ( A_{1} \vee A_{2} \bigr ) (g) : \mathbb {T}_{\textsf{s}} \rightarrow \mathbb {T}_{\textsf{t}}$ is the function such that, for every state $s \in \mathbb {T}_{\textsf{s}}$:

    $$\begin{aligned}{}[\textsf{den}^{\mathfrak {A}}( A_{1} \vee A_{2}) (g)] (s)&=V \in \mathbb {T}_{\textsf{t}}, \ \text {where }V\text { is as in } (\text {19a})-(\text {19c}) \end{aligned}$$

    (18)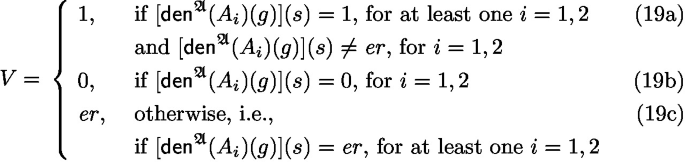

    

  The definition of $\textsf{den}^{\mathfrak {A}}( A_{1} \rightarrow A_{2}) (g)$ is in a similar mode.

• (D6) $\textsf{den}^{\mathfrak {A}} \bigl ( \lnot (A) \bigr ) (g) : \mathbb {T}_{\textsf{s}} \rightarrow \mathbb {T}_{\textsf{t}}$ is such that, for every state $s \in \mathbb {T}_{\textsf{s}}$:

  

• (D7) Pure Universal Quantifier $\forall$:¹

  • (D7a) For the state-independent quantifier $\forall$ ($\tau = \textsf{t}$), the definition is similar to the state dependent one, and we do not present its details

  • (D7b) For the state-dependent quantifier $\forall$ ($\tau = \, \widetilde{\textsf{t}}$), for every state $s \in \mathbb {T}_{\textsf{s}}$:

    $\bigl [ \textsf{den}^{\mathfrak {A}} \bigl ( \forall (v^{\sigma }) (B^{\tau }) \bigr ) (g) \bigr ] (s) = V$, where:

    

• (D8) Pure Existential Quantifier $\exists$:

  • (D8a) For the state-independent quantifier $\exists$, with $\tau = \textsf{t}$, the definition is similar to the state dependent one, and we do not present it here

  • (D8b) For the state-dependent quantifier $\exists$, ($\tau = \, \widetilde{\textsf{t}}$), for every state $s \in \mathbb {T}_{\textsf{s}}$:

    $\bigl [ \textsf{den}^{\mathfrak {A}} \bigl ( \exists (v^{\sigma }) (B^{\tau }) \bigr ) (g) \bigr ] (s) = V$, where:

    

Often, we shall skip the superscript in $G^{\mathfrak {A}}$ and $\textsf{den}^{\mathfrak {A}}$, by writing G and $\textsf{den}$.

3 Gamma-Star Reduction Calculus of $\text {L}^{\lambda }_{\text {ar}}$

I designate the logic operators as a set of specialised, logic constants. In this way, I classify the reduction rules for the terms formed by (3e)–(3f) as special cases of the reduction rule for application terms.

In this section, I extend the set of the $\text {L}^{\lambda }_{\text {ar}}$-reduction rules introduced in [18], by adding:

• (1) the reduction rules ($\xi$) for the quantifier terms (3g) together with the $\lambda$-abstract terms, $\xi \in \{\, \lambda , \exists , \forall \,\}$

• (2) an additional reduction rule, the ($\gamma ^*$) rule, (30a)–(30b), which extends the corresponding rule in [7]

3.1 Congruence Relation Between Terms

Definition 8

The congruence relation is the smallest equivalence relation (i.e., reflexive, symmetric, transitive) between terms $\mathrel {\equiv _{\textsf{c}}}{} \subseteq {\textsf{Terms}}\times {\textsf{Terms}}$, that is closed under:

• (1) operators of term-formation:

  • application, which includes logic constants because we introduced them as categorematic constants

  • $\lambda$-abstraction and pure, logic quantifiers

  • acyclic recursion

    $$\begin{aligned} &\text {If }A \mathrel {\equiv _{\textsf{c}}}A'\text { and }B \mathrel {\equiv _{\textsf{c}}}B', \text { then }A(B) \mathrel {\equiv _{\textsf{c}}}A'(B') \end{aligned}$$

    (ap-congr)
    $$\begin{aligned} &\text {If }A \mathrel {\equiv _{\textsf{c}}}B,\text { and }\xi \in \{\, \lambda , \exists , \forall \,\}, \text { then }\xi (u) (A) \mathrel {\equiv _{\textsf{c}}}\xi (u) (B) \end{aligned}$$

    (lq-congr)
    $$\begin{aligned} &\begin{aligned} &\text {If }A_i \mathrel {\equiv _{\textsf{c}}}B_i,\text { for }i = 0, \dots , n,\text { then: } \\ & \qquad A_{0} \mathrel {\textsf{where}}\{\, p_{1} \mathrel {\mathop :}=A_{1}, \dots , p_{n} \mathrel {\mathop :}=A_{n} \,\} \\ & \mathrel {\equiv _{\textsf{c}}}{} B_{0} \mathrel {\textsf{where}}\{\, p_{1} \mathrel {\mathop :}=B_{1}, \dots , p_{n} \mathrel {\mathop :}=B_{n} \,\} \end{aligned} \end{aligned}$$

    (rec-congr)

• (2) renaming bound pure and recursion variables without variable collisions, by free replacements, see Definition 3

  • (a) renaming pure variables bound by $\lambda$-abstraction and pure, logic quantifiers

    $$\begin{aligned} \begin{aligned} &\xi (x) (A) \mathrel {\equiv _{\textsf{c}}}{} \xi (y) (A\{ x \mathrel {\mathop :}\equiv y\}), \quad \text {for } x, y \in \textsf{PureV}_{\tau }, \xi \in \{\, \lambda , \exists , \forall \,\}\\ & \text {assuming } y \in \textsf{FreeV}(A)\text { and } y\text { is free for (replacing) }x\text { in }A \end{aligned} \end{aligned}$$

    (24a)

  • (b) renaming memory location (variables) bound by the recursion operator $\mathrel {\textsf{where}}$, in assignments

    $$\begin{aligned} \begin{aligned} A\equiv {} & A_{0} \mathrel {\textsf{where}}\lbrace \, p_{1} \mathrel {\mathop :}=A_{1}, \ldots , p_{n} \mathrel {\mathop :}=A_{n} \,\rbrace \\ \mathrel {\equiv _{\textsf{c}}}{} &A'_{0} \mathrel {\textsf{where}}\lbrace \, p'_{1} \mathrel {\mathop :}=A'_{1}, \ldots , p'_{n} \mathrel {\mathop :}=A'_{n} \,\rbrace \end{aligned} \end{aligned}$$

    (25a)
    $$\begin{aligned} \begin{aligned} & \text {assuming } p'_{i}\not \in \textsf{FreeV}(A)\text { and } p'_{i}\text { is free for (replacing) }p_{i}\text { in }A_{j} \\ A'_{j}&\equiv A_{j} \{ p_{1} \mathrel {\mathop :}\equiv p'_{1}, \dots , p_{n} \mathrel {\mathop :}\equiv p'_{n} \} \equiv A_{j} \{ \overrightarrow{p} \mathrel {\mathop :}\equiv \overrightarrow{p'} \}, \ j \in \{ 0, \dots , n \}\\ & i \in \{ 1, \dots , n \}, \ j \in \{ 0, \dots , n \} \end{aligned} \end{aligned}$$

    (25b)

• (3) re-ordering of the assignments within the recursion terms

  $$\begin{aligned} \begin{aligned} & \text {for every permutation }\pi : \{1, \ldots , n \} \mathrel {\xrightarrow [\textsf{onto}]{\mathsf {1-to-1}}}\{1, \ldots , n \} \\ & A_0 \mathrel {\textsf{where}}\lbrace \, p_1 \mathrel {\mathop :}=A_1, \ldots , p_n \mathrel {\mathop :}=A_n \,\rbrace \\ \mathrel {\equiv _{\textsf{c}}}{} & A_0 \mathrel {\textsf{where}}\lbrace \, p_{\pi (1)} \mathrel {\mathop :}=A_{\pi (1)}, \ldots , p_{\pi (n)} \mathrel {\mathop :}=A_{\pi (n)} \,\rbrace \end{aligned} \end{aligned}$$

  (26)

3.2 Reduction Rules of Extended $\text {L}^{\lambda }_{\text {ar}}$

In this section, we define the set ${\textsf{RedR}}$ of the reduction rules of TTA, which are the same for its variants of full and acyclic recursion $\text {L}^{\lambda }_{r}$ and $\text {L}^{\lambda }_{\text {ar}}$, respectively.

$$\begin{aligned} {{\textbf {Congruence}}} & \qquad \qquad \qquad \text {If }A \mathrel {\equiv _{\textsf{c}}}B,\text { then }A \mathrel {\Rightarrow }B \end{aligned}$$

(cong)

$$\begin{aligned} {{\textbf {Transitivity}}} & \qquad \qquad \qquad \text {If }A \mathrel {\Rightarrow }B\text { and } B \mathrel {\Rightarrow }C, \text { then }A \mathrel {\Rightarrow }C \end{aligned}$$

(trans)

• Compositionality Replacement of sub-terms with correspondingly reduced ones respects the term structure by the definition of the term syntax:

  $$\begin{aligned} &\text {If }A \mathrel {\Rightarrow }A'\text { and }B \mathrel {\Rightarrow }B', \text { then } A(B) \mathrel {\Rightarrow }A'(B') \end{aligned}$$

  (ap-comp)
  $$\begin{aligned} &\text {If }A \mathrel {\Rightarrow }B,\text { and }\xi \in \{\, \lambda , \exists , \forall \,\},\text { then }\xi (u) (A) \mathrel {\Rightarrow }\xi (u) (B) \end{aligned}$$

  (lq-comp)
  $$\begin{aligned} \begin{aligned} &\text {If }A_i \mathrel {\Rightarrow }B_i, \text {for }i = 0, \dots , n,\text { then }\\ & \quad \ A_{0} \mathrel {\textsf{where}}\{\, p_{1} \mathrel {\mathop :}=A_{1}, \dots , p_{n} \mathrel {\mathop :}=A_{n} \,\}\\ & \mathrel {\Rightarrow }{} B_{0} \mathrel {\textsf{where}}\{\, p_{1} \mathrel {\mathop :}=B_{1}, \dots , p_{n} \mathrel {\mathop :}=B_{n} \,\} \end{aligned} \end{aligned}$$

  (rec-comp)

• Head Rule Given that, for all $i=1$, ..., n, $j=1$, ..., m, $p_i \not = q_{j}$ and $p_i$ does not occur freely in $B_j$:

  $$\begin{aligned} \begin{aligned} &\bigl (A_{0} \mathrel {\textsf{where}}\lbrace \, \overrightarrow{p} \mathrel {\mathop :}=\overrightarrow{A} \, \rbrace \bigr ) \mathrel {\textsf{where}}\lbrace \, \overrightarrow{q} \mathrel {\mathop :}=\overrightarrow{B} \, \rbrace \\ \mathrel {\Rightarrow }{} & A_{0} \mathrel {\textsf{where}}\lbrace \, \overrightarrow{p} \mathrel {\mathop :}=\overrightarrow{A}, \ \overrightarrow{q} \mathrel {\mathop :}=\overrightarrow{B} \, \rbrace \end{aligned} \end{aligned}$$

  (head)

• Bekič-Scott Rule Given that, for all $i=1$, ..., n, $j=1$, ..., m, $p_i \not = q_{j}$ and $q_j$ does not occur freely in $A_i$

  $$\begin{aligned} & A_{0} \mathrel {\textsf{where}}\lbrace \, p \mathrel {\mathop :}=\bigl (B_{0} \mathrel {\textsf{where}}\lbrace \, \overrightarrow{q} \mathrel {\mathop :}=\overrightarrow{B} \, \rbrace \bigr ), \overrightarrow{p} \mathrel {\mathop :}=\overrightarrow{A} \, \rbrace \nonumber \\ \mathrel {\Rightarrow }{} &A_{0} \mathrel {\textsf{where}}\lbrace \, p \mathrel {\mathop :}=B_{0}, \overrightarrow{q} \mathrel {\mathop :}=\overrightarrow{B}, \ \overrightarrow{p} \mathrel {\mathop :}=\overrightarrow{A} \, \rbrace \end{aligned}$$

  (B-S)

• Recursion-Application Rule Given that, for all $i=1$, ..., n, $p_i$ does not occur freely in B

  $$\begin{aligned} & (A_{0} \mathrel {\textsf{where}}\lbrace \, \overrightarrow{p} \mathrel {\mathop :}=\overrightarrow{A} \, \rbrace \bigr )(B) \mathrel {\Rightarrow }{} A_{0}(B) \mathrel {\textsf{where}}\lbrace \, \overrightarrow{p} \mathrel {\mathop :}=\overrightarrow{A} \,\rbrace \end{aligned}$$

  (recap)

• Application Rule Given that $B \in {\textsf{Terms}}$ is proper and $b \in \textsf{RecV}$ is fresh, i.e., $b \in \bigl [ \textsf{RecV}- \big (\textsf{FreeV}\big (A(B)\big ) \cup \textsf{BoundV}\big (A(B)\big ) \big ) \bigr ]$,

  $$\begin{aligned} A(B) &\mathrel {\Rightarrow }\ A(b) \mathrel {\textsf{where}}\lbrace \, b \mathrel {\mathop :}=B \, \rbrace \end{aligned}$$

  (ab)

• $\lambda$ and Quantifier Rules Let $\xi \in \{\, \lambda , \exists , \forall \,\}$

  

  given that, for every $i = 1$, ..., n ($n \ge 0$), $p'_i \in \textsf{RecV}$ is a fresh recursion (memory) variable, and $A'_i$ ($0\le i \le n$) is the result of the replacement of all the free occurrences of $p_{1}, \dots , p_{n}$ in $A_i$ with $p'_{1}(u), \dots , p'_{n}(u)$, respectively, i.e.:

  $$\begin{aligned} A'_i &\equiv A_i \{ p_{1} \mathrel {\mathop :}\equiv p'_{1}(u), \dots , p_{n} \mathrel {\mathop :}\equiv p'_{n}(u) \} \equiv A_i \{ \overrightarrow{p} \mathrel {\mathop :}\equiv \overrightarrow{p'(u)} \} \ (0\le i \le n) \end{aligned}$$

  (29)

• $\gamma ^*$-Rule

  

given that:

• the term $A \in {\textsf{Terms}}$ satisfies the $\gamma ^*$-condition (given in Definition 9) for the assignment $p \mathrel {\mathop :}=\lambda (\overrightarrow{u})\lambda (v)P : (\overrightarrow{\vartheta } \rightarrow (\vartheta \rightarrow \tau ) )$

• $p' \in \textsf{RecV}_{(\overrightarrow{\vartheta } \rightarrow \tau )}$ is a fresh recursion variable

• for each part $X_i$ of $\overrightarrow{X}$ in ($\gamma ^*$) and (30b) (i.e., for each $X_i \equiv A_i$ in $\overrightarrow{X} \equiv \overrightarrow{A}$, and each $X_i \equiv B_i$ in $\overrightarrow{X} \equiv \overrightarrow{B}$), $X'_i$ is the result of the free replacements $X'_i \equiv X_i\{ \, p(\overrightarrow{u})(v) \mathrel {\mathop :}\equiv p'(\overrightarrow{u}) \, \}$ of all occurrences of $p(\overrightarrow{u})(v)$ by $p'(\overrightarrow{u})$ (in the free occurrences of p), modulo renaming the variables $\overrightarrow{u}, v$, for $i \in \{0, \ldots , n_X \}$, i.e.:

  $$\begin{aligned} \overrightarrow{X'} \equiv \overrightarrow{X}\{ \, p(\overrightarrow{u})(v) \mathrel {\mathop :}\equiv p'(\overrightarrow{u}) \, \} \end{aligned}$$

  (31)

Definition 9

($\gamma ^*$-Condition). Assume that $i=1, \dots , n$ ($n \ge 0$), $\tau , \vartheta , \vartheta _i \in \textsf{Types}$, $u, u_i \in \textsf{PureV}$, $p \in \textsf{RecV}$, $P \in {\textsf{Terms}}$, are such that $u : \vartheta$, $u_i : \vartheta _i$, $p : (\overrightarrow{\vartheta } \rightarrow (\vartheta \rightarrow \tau ) )$, $P : \tau$, and thus, $\lambda (\overrightarrow{u}^{\overrightarrow{\vartheta }} ) \lambda (v^{\vartheta }) (P^{\tau }) : (\overrightarrow{\vartheta } \rightarrow (\vartheta \rightarrow \tau ) )$.

A recursion term $A \in {\textsf{Terms}}$ satisfies the $\gamma ^*$-condition for an assignment $p \mathrel {\mathop :}=\lambda (\overrightarrow{u}^{\overrightarrow{\vartheta }} ) \lambda (v^{\vartheta }) (P^{\tau }) : (\overrightarrow{\vartheta } \rightarrow (\vartheta \rightarrow \tau ) )$, with respect to $\lambda (v)$, if and only if A is of the form (32)

$$\begin{aligned} A &\equiv A_{0} \mathrel {\textsf{where}}\lbrace \, \overrightarrow{a} \mathrel {\mathop :}=\overrightarrow{A}, \ p \mathrel {\mathop :}=\lambda (\overrightarrow{u}) \lambda (v)P, \ \overrightarrow{b} \mathrel {\mathop :}=\overrightarrow{B} \,\rbrace \end{aligned}$$

(32)

with the sub-terms of appropriate types, such that the following holds:

• (1) $P \in {\textsf{Terms}}_{\tau }$ does not have any free occurrences of v, i.e., $v \not \in \textsf{FreeVars}(P)$

• (2) All occurrences of p in $A_{0}$, $\overrightarrow{A}$, and $\overrightarrow{B}$ are free with respect to p (by renaming bound occurrences of recursion variables) and are occurrences in sub-terms $p(\overrightarrow{u})(v)$, which are in binding scope of $\xi _{1} (u_{1}), \dots , \xi _{n} (u_{n}), \xi (v)$, for $\xi _{i}, \xi \in \{\, \lambda , \exists , \forall \,\}$, modulo renaming the bound variables $\overrightarrow{u}, v$, $i=1, \dots , n$ ($n \ge 0$)

Note: If we take away the second part of (2), which requires $p(\overrightarrow{u})(v)$ to be within the binding scopes of $\overrightarrow{\xi (u)}, \, \xi (v)$, the ($\gamma ^*$) rule may remove free occurrences of pure variables, e.g., v in $p(\overrightarrow{u})(v)$, from some of the parts of the terms. This (strong) form of the $\gamma ^*$-condition is introduced in [7].

When a recursion term A of the form (32) satisfies the $\gamma ^*$-condition, given in Definition 9, we also say that the assignment $p \mathrel {\mathop :}=\lambda (\overrightarrow{u}) \lambda (v) P$ satisfies the $\gamma ^*$-condition, for any term $A'$ such that $A' \mathrel {\equiv _{\textsf{c}}}A$, i.e., modulo congruence.

Definition 10

($\gamma ^*$-Rules). We shall call the set ${\textsf{RedR}}$ of the reduction rules (cong)–($\xi$), ($\gamma ^*$), $\gamma ^*$-reduction rules and also, simply $\text {L}^{\lambda }_{\text {ar}}$-reduction rules.

3.3 Reduction Relation

The extended set of reduction rules of $\text {L}^{\lambda }_{\text {ar}}$, (cong)–($\xi$), ($\gamma ^*$), given in Sect. 3.2, defines the extended reduction relation $\mathrel {\Rightarrow ^{*}_{\gamma ^*}}$ between $\text {L}^{\lambda }_{\text {ar}}$-terms, $A \mathrel {\Rightarrow ^{*}_{\gamma ^*}}B$, by the alternatively expressed, equivalent Definition 11 and Definition 12.

Definition 11

The $\gamma ^*$-reduction relation $\mathrel {\Rightarrow ^{*}_{\gamma ^*}}$ between terms is the smallest relation $\mathrel {\Rightarrow ^{*}_{\gamma ^*}}\subseteq {\textsf{Terms}}\times {\textsf{Terms}}$, which is the reflexive and transitive closure of the immediate reductions by any of the reduction rules (cong)–($\xi$), ($\gamma ^*$).

Definition 12

($\gamma ^*$-Reduction). For all $A, B \in {\textsf{Terms}}$, $A \mathrel {\Rightarrow ^{*}_{\gamma ^*}}B$ iff there is a sequence of consecutive, immediate reductions by (cong)–($\gamma ^*$), i.e.:

$$\begin{aligned} A \mathrel {\Rightarrow ^{*}_{\gamma ^*}}B \iff &\text {there exist }A_{i} \in {\textsf{Terms}}, 0 \le i < n,\text { such that:} \nonumber \\ & A \equiv A_{0}, \ A_{n} \equiv B, \text { and } \end{aligned}$$

(33)

$$\begin{aligned} & A_{i} \mathrel {\Rightarrow }A_{i+1}, \text { for some of the rules } \hbox {(cong)}-(\gamma ^*) \nonumber \\ \iff &\text { (abbreviated) } A \equiv A_{0} \mathrel {\Rightarrow }\dots \mathrel {\Rightarrow }A_{n} \equiv B \ (n \ge 0) \end{aligned}$$

(34)

Often, we shall write $A \mathrel {\Rightarrow }B$ instead of $A \mathrel {\Rightarrow ^{*}_{\gamma ^*}}B$, including when applying none or more than one rule.

Lemma 1

($\gamma ^*$-Reducing Multiple, Innessential $\lambda$ -Abstractions in an Assignment). Assume that $A \in {\textsf{Terms}}$ is of the form (35a)–(35b):

$$\begin{aligned} A &\equiv A_{0} \mathrel {\textsf{where}}\lbrace \, \overrightarrow{a} \mathrel {\mathop :}=\overrightarrow{A}, \ b \mathrel {\mathop :}=\lambda (\overrightarrow{u_1}) \lambda (v_1) \dots \lambda (\overrightarrow{u_k}) \lambda (v_k) \lambda (\overrightarrow{u_{k+1}}) B, \end{aligned}$$

(35a)

$$\begin{aligned} & \qquad \qquad \qquad \overrightarrow{c} \mathrel {\mathop :}=\overrightarrow{C} \,\rbrace \end{aligned}$$

(35b)

such that A satisfies the $\gamma ^*$-condition in Definition 9 for the assignment for b in (35a), with respect to all $\lambda$-abstractions $\lambda (v_j)$, for $1 \le j \le k$, $k \in \mathbb {N}$, $k \ge 1$.

Then, the following reductions (36a)– (36b) can be done:

$$\begin{aligned} A \mathrel {\Rightarrow ^{*}_{\gamma ^*}}{} & A_{0}^{k} \mathrel {\textsf{where}}\lbrace \, \overrightarrow{a} \mathrel {\mathop :}=\overrightarrow{A^{k}}, \ b^{k} \mathrel {\mathop :}=\lambda (\overrightarrow{u_1}) \dots \lambda (\overrightarrow{u_k}) \lambda (\overrightarrow{u_{k+1}}) B, \end{aligned}$$

(36a)

$$\begin{aligned} & \qquad \qquad \quad \overrightarrow{c} \mathrel {\mathop :}=\overrightarrow{C^{k}} \,\rbrace \end{aligned}$$

(36b)

where for each part $X_i$ of $\overrightarrow{X}$ in (35a)–(35b) (i.e., for $X_i \equiv A_i$ in $\overrightarrow{X} \equiv \overrightarrow{A}$ or $X_i \equiv C_i$ in $\overrightarrow{X} \equiv \overrightarrow{C}$) $X^{k}_i$ in $\overrightarrow{X^{k}}$ is the result of the replacements (37a)–(37b), modulo renaming the bound variables $\overrightarrow{u_l}, v_j$, for $i \in \{0, \ldots , n_{X} \}$:

$$\begin{aligned} & \begin{aligned} X_i^{k} &\equiv X_i \{ \, b (\overrightarrow{u_1}) (v_1) \dots (\overrightarrow{u_k}) (v_k) (\overrightarrow{u_{k+1}}) \mathrel {\mathop :}\equiv b^{k} (\overrightarrow{u_1}) \dots (\overrightarrow{u_k}) (\overrightarrow{u_{k+1}}) \, \} \\ &\text {for }i \in \{0, \ldots , n_{X} \} \end{aligned} \end{aligned}$$

(37a)

$$\begin{aligned} &\overrightarrow{X^{k}} \equiv \overrightarrow{X^{k}} \{ \, b (\overrightarrow{u_1}) (v_1) \dots (\overrightarrow{u_k}) (v_k) (\overrightarrow{u_{k+1}}) \mathrel {\mathop :}\equiv b^{k} (\overrightarrow{u_1}) \dots (\overrightarrow{u_k}) (\overrightarrow{u_{k+1}}) \, \} \end{aligned}$$

(37b)

Proof

The proof is by induction on $k \in \mathbb {N}$, for $\text {L}^{\lambda }_{\text {ar}}$ extended by ($\xi$) and ($\gamma ^*$) rules, for $\xi \in \{\, \lambda , \exists , \forall \,\}$. We do not provide it here, because it is long. For such a lemma about the $\text {L}^{\lambda }_{\text {ar}}$, without logic operators and pure quantifiers, see [4, 7].    $\square$

Lemma 2

($\gamma ^*$-Reduction of the Assignments of a Recursion Term). For every recursion term $P \equiv {} P_0 \mathrel {\textsf{where}}\lbrace \, \overrightarrow{p} \mathrel {\mathop :}=\overrightarrow{P} \,\rbrace$, (38a), there is a term Q of the form in (38b), such that Q does not satisfy the $\gamma ^*$-condition in Definition 9, for any of its assignments $q_i \mathrel {\mathop :}=Q_i$ ($i = 1, \dots , n$) in (38b), and $P \mathrel {\Rightarrow ^{*}_{\gamma ^*}}Q$, abbreviated by $P \mathrel {\Rightarrow }Q$.

$$\begin{aligned} &P \equiv P_0 \mathrel {\textsf{where}}\lbrace \, p_1 \mathrel {\mathop :}=P_1, \ldots , p_n \mathrel {\mathop :}=P_n \,\rbrace \equiv {} P_0 \mathrel {\textsf{where}}\lbrace \, \overrightarrow{p} \mathrel {\mathop :}=\overrightarrow{P} \,\rbrace \end{aligned}$$

(38a)

$$\begin{aligned} \mathrel {\Rightarrow ^{*}_{\gamma ^*}}{} &Q \equiv Q_0 \mathrel {\textsf{where}}\lbrace \, q_1 \mathrel {\mathop :}=Q_1, \ldots , q_n \mathrel {\mathop :}=Q_n \,\rbrace \equiv {} Q_0 \mathrel {\textsf{where}}\lbrace \, \overrightarrow{q} \mathrel {\mathop :}=\overrightarrow{Q} \,\rbrace \end{aligned}$$

(38b)

Proof

See [4] extended by ($\xi$) and ($\gamma ^*$) rules, for $\xi \in \{\, \lambda , \exists , \forall \,\}$.    $\square$

Definition 13

($\gamma ^*$-Irreducible Terms). We say that a term $A \in {\textsf{Terms}}$ is $\gamma ^*$-irreducible if and only if (39) holds:

$$\begin{aligned} \text {for all }B \in {\textsf{Terms}}, \quad A \mathrel {\Rightarrow ^{*}_{\gamma ^*}}B &\implies A \mathrel {\equiv _{\textsf{c}}}B \end{aligned}$$

(39)

3.4 Canonical Forms and $\gamma ^*$-Reduction

Theorem 1

($\gamma ^*$-Canonical Form: Existence and Uniqueness of Canonical Forms). See [6,7,8, 18]. For every term $A \in {\textsf{Terms}}$, the following hold:

• (1) (Existence of a $\gamma ^*$-canonical form of A) There exist explicit, $\gamma ^*$-irreducible $A_{0}, \dots , A_{n} \in {\textsf{Terms}}$ ($n \ge 0$), such that the term $\textsf{cf}_{\gamma ^*}(A)$ that is of the form (40) is $\gamma ^{*}$-irreducible, i.e., irreducible and does not satisfy the $\gamma$-condition:

  $$\begin{aligned} \textsf{cf}_{\gamma ^*}(A) &\equiv {} A_0 \mathrel {\textsf{where}}\lbrace \, p_1 \mathrel {\mathop :}=A_1 , \ldots , p_n \mathrel {\mathop :}=A_n \,\rbrace \end{aligned}$$

  (40)

  Thus, $\textsf{cf}_{\gamma ^*}(A)$ is $\gamma ^*$-irreducible.

• (2) A and $\textsf{cf}_{\gamma ^*}(A)$ have the same constants and free variables:

  $$\begin{aligned} \textsf{Consts}(A) &= \textsf{Consts}(\textsf{cf}_{\gamma ^*}(A))\end{aligned}$$

  (41a)
  $$\begin{aligned} \textsf{FreeV}(A) &= \textsf{FreeV}(\textsf{cf}_{\gamma ^*}(A)) \end{aligned}$$

  (41b)

• (3) $A \mathrel {\Rightarrow ^{*}_{\gamma ^*}}\textsf{cf}_{\gamma ^*}(A)$

• (4) If A is $\gamma ^*$-irreducible, then $A \mathrel {\equiv _{\textsf{c}}}\textsf{cf}_{\gamma ^*}(A)$

• (5) If $A \mathrel {\Rightarrow ^{*}_{\gamma ^*}}B$, then $\textsf{cf}_{\gamma ^*}(A) \mathrel {\equiv _{\textsf{c}}}\textsf{cf}_{\gamma ^*}(B)$

• (6) (Uniqueness of $\textsf{cf}_{\gamma ^*}(A)$ with respect to congruence) For every $B \in {\textsf{Terms}}$, such that $A \mathrel {\Rightarrow ^{*}_{\gamma ^*}}B$ and B is $\gamma ^*$-irreducible, it holds that $B \mathrel {\equiv _{\textsf{c}}}\textsf{cf}_{\gamma ^*}(A)$, i.e., $\textsf{cf}_{\gamma ^*}(A)$ is unique, up to congruence. We write:

  $$\begin{aligned} A &\mathrel {\Rightarrow _{\textsf{cf}_{\gamma ^*}}}B \iff B \mathrel {\equiv _{\textsf{c}}}\textsf{cf}_{\gamma }(A) \end{aligned}$$

  (42)

Proof

The proof is by induction on term structure of A, in Definition 1, i.e., (3a)–(3g), using reduction rules, and properties of the extended $\gamma ^*$-reduction relation.

Note: the reduction rules don’t remove or add any constants and free variables.    $\square$

Algorithmic Semantics. The algorithmic meaning of a proper $A \in {\textsf{Terms}}$, i.e., a non-immediate, algorithmically meaningful term, is designated by $\textsf{alg}(A)$ and is determined by its canonical form $\textsf{cf}(A)$.

Informally, for each proper $A\in {\textsf{Terms}}$, the algorithm $\textsf{alg}(A)$ for computing its denotation $\textsf{den}(A)$ consists of computations provided by the basic parts $A_{i}$ of its canonical form $\textsf{cf}(A) \equiv {A_0 \mathrel {\textsf{where}}\{p_1:= A_1, \ldots , p_n:= A_n}\}$, according to their structural rank, by recursive iteration.

For every $A \in {\textsf{Terms}}$, $\textsf{cf}(A)$, i.e., $\textsf{cf}_{\gamma ^*}(A)$, is obtained from A by the reduction calculus of $\text {L}^{\lambda }_{\text {ar}}$, introduced in Sect. 3.2.

Definition 14

(Algorithmic Equivalence). Assume a given semantic structure $\mathfrak {A}$. For all $A, B \in {\textsf{Terms}}$, A and B are $\gamma ^{*}$-algorithmically equivalent (i.e., synonymous) in $\mathfrak {A}$, $A \mathrel {\approx _{\gamma ^*}}B$ iff

• A and B are both immediate, or

• A and B are both proper

and, in each of these cases, there are explicit, $\gamma ^{*}$-irreducible terms (of appropriate types), $A_0$, ..., $A_n$, $B_0$, ..., $B_n$, $n \ge 0$, such that:

• (1) $A \mathrel {\Rightarrow ^{*}_{\gamma ^*}}A_{0} \mathrel {\textsf{where}}\{\, p_1 \mathrel {\mathop :}=A_1, \ldots , p_n \mathrel {\mathop :}=A_n \,\} \equiv \textsf{cf}_{\gamma ^*}(A)$

• (2) $B \mathrel {\Rightarrow ^{*}_{\gamma ^*}}B_{0} \mathrel {\textsf{where}}\{\, q_1 \mathrel {\mathop :}=B_1 , \ldots , q_n \mathrel {\mathop :}=B_n \,\} \equiv \textsf{cf}_{\gamma ^*}(B)$

• (3) for all $i \in \{ \, 0, \ldots , n \, \}$:

  $$\begin{aligned} \textsf{den}^{\mathfrak {A}}(A_i)(g) &= \textsf{den}^{\mathfrak {A}}(B_i)(g), \ \text {for every variable valuation }g\in G \end{aligned}$$

  (43a)
  $$\begin{aligned} \textsf{den}^{\mathfrak {A}}(A_i) &= \textsf{den}^{\mathfrak {A}}(B_i) \end{aligned}$$

  (43b)

When $A \mathrel {\approx _{\gamma ^*}}B$, we say that A and B are algorithmically $\gamma ^*$-equivalent, alternatively, that A and B are $\gamma ^*$-synonymous. Sometimes, we skip the label $\gamma ^{*}$.

4 Algorithmic Expressiveness of $\text {L}^{\lambda }_{\text {ar}}$

Moschovakis [18], via Theorem §3.24, proves that $\text {L}^{\lambda }_{\text {ar}}$ is a proper extension of Gallin $\textrm{TY}_2$, see Gallin [1]. Gallin [1], via his Theorem 8.2, can provide an interpretation of Montague IL [14] into $\textrm{TY}_2$. Suitable interpretation can be given in $\text {L}^{\lambda }_{\text {ar}}$ ($\text {L}^{\lambda }_{r}$), too. That is not our purpose in this paper.

Theorem 2, has the same formulation as Theorem §3.24 in [18]. The difference is that Theorem 2 covers the extended $\text {L}^{\lambda }_{\text {ar}}$ and its $\mathrel {\Rightarrow ^{*}_{\gamma ^*}}$ reduction.

Theorem 2

(Conditions for Explicit and Non-Explicit Terms). See Theorem §3.24, Moschovakis [18].

• (1) Necessary Condition for Explicit Terms: For any explicit $A \in {\textsf{Terms}}$, there is no memory (recursion) location that occurs in more than one part $A_{i}$ ($0 \le i \le n$) of $\textsf{cf}_{\gamma ^*}(A)$

• (2) Sufficient Condition for Non-Explicit Terms: Assume that $A \in {\textsf{Terms}}$ is such that a location $p \in \textsf{RecV}$ occurs in (at least) two parts of $\textsf{cf}(A)$, and respectively, of $\textsf{cf}_{\gamma ^*}(A)$, and the denotations of those parts depend essentially on p:

  $$\begin{aligned} &A \mathrel {\Rightarrow ^{*}_{\gamma ^*}}\textsf{cf}_{\gamma ^*}(A) \equiv {} A_0 \mathrel {\textsf{where}}\lbrace \, p_1 \mathrel {\mathop :}=A_1 , \ldots , p_n \mathrel {\mathop :}=A_n \,\rbrace \end{aligned}$$

  (44a)
  $$\begin{aligned} &p \in \textsf{FreeV}(A_{k}), \quad p \in \textsf{FreeV}(A_{l}) \ (k \ne l) \end{aligned}$$

  (44b)
  $$\begin{aligned} & \textsf{den}(A_{k}) (g \{ p \mathrel {\mathop :}\equiv r\}) \ne \textsf{den}(A_{k}) (g \{ p \mathrel {\mathop :}\equiv r'\}), \ \text {for some }r, r' \in \mathbb {T}_{\sigma } \end{aligned}$$

  (44c)
  $$\begin{aligned} & \textsf{den}(A_{l}) (g \{ p \mathrel {\mathop :}\equiv r\}) \ne \textsf{den}(A_{l}) (g \{ p \mathrel {\mathop :}\equiv r'\}), \ \text {for some }r, r' \in \mathbb {T}_{\sigma } \end{aligned}$$

  (44d)

  Then, there is no explicit term to which A is algorithmically equivalent.

The proof of Theorem §3.24, Moschovakis [18] is extended for the logic operators, pure quantifiers and the $\gamma ^*$-reduction.    $\square$

The extended, algorithmic expressiveness of $\text {L}^{\lambda }_{\text {ar}}$ is demonstrated by the terms in the following examples, which provide specific instantiations of algorithmic patterns of large classes and subtle semantic distinctions.

Logic Quantifiers and Reductions with Quantifier Rules: Assume that $\text {L}^{\lambda }_{\text {ar}}$ has $cube , large _{0} \in \textsf{Consts}_{(\widetilde{\textsf{e}} \rightarrow \, \widetilde{\textsf{t}})}$, and $large \in \textsf{Consts}_{((\widetilde{\textsf{e}} \rightarrow \, \widetilde{\textsf{t}})\rightarrow (\widetilde{\textsf{e}} \rightarrow \, \widetilde{\textsf{t}}))}$ as a modifier.

$$\begin{aligned} &\text {Some cube is large} \xrightarrow {\textsf{render}}{} B \equiv {} \exists x ( cube (x) \wedge large _{0} (x) ) \end{aligned}$$

(45a)

$$\begin{aligned} B & \mathrel {\Rightarrow }{} \exists x ( (c \wedge l) \mathrel {\textsf{where}}\{\, c \mathrel {\mathop :}= cube (x), \, l \mathrel {\mathop :}= large _{0} (x) \,\} ) \end{aligned}$$

(45b)

$$\begin{aligned} & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \qquad \ \ \ \mathrm{{2x}}\mathrm {(ap)} \mathrm {\ to\ } \wedge ; \text {(lq-comp)} \nonumber \\ & \mathrel {\Rightarrow }{} \underbrace{ \exists x (c'(x) \wedge l'(x)) }_{B_{0} \text { algorithmic pattern} } \mathrel {\textsf{where}}\{\, \end{aligned}$$

(45c)

$$\begin{aligned} &\qquad \ \underbrace{ c' \mathrel {\mathop :}=\lambda (x) ( cube (x)), \, l' \mathrel {\mathop :}=\lambda (x) ( large _{0} (x)) }_{\text {instantiations of memory slots }c', l' } \,\} \end{aligned}$$

(45d)

$$\begin{aligned} & \equiv {} \textsf{cf}(B) \quad \ \text {from }\text {(45b)},\text { by }(\xi )\text { to }\exists \nonumber \\ &\approx \underbrace{ \exists x (c'(x) \wedge l'(x)) }_{B_{0} \text { algorithmic pattern} } \mathrel {\textsf{where}}\{ \underbrace{ c' \mathrel {\mathop :}= cube , \, l' \mathrel {\mathop :}= large _{0} }_{\text {instantiations of memory slots }c', l'} \} \equiv {} B' \end{aligned}$$

(45e)

$$\begin{aligned} &\begin{aligned} &\text {by Definition}~14 \text { from }\text {(45c)}-\text {(45d)}, \textsf{den}(\lambda (x) ( cube (x))) = \textsf{den}( cube ), \\ & \qquad \qquad \qquad \qquad \qquad \qquad { \textsf{den}(\lambda (x) ( large _{0}(x) ) ) = \textsf{den}( large _{0} ) } \end{aligned} \end{aligned}$$

(45f)

Repeated Calculations:

$$\begin{aligned} &\text {Some cube is large} \xrightarrow {\textsf{render}}{} T, \quad large \in \textsf{Consts}_{((\widetilde{\textsf{e}} \rightarrow \, \widetilde{\textsf{t}})\rightarrow (\widetilde{\textsf{e}} \rightarrow \, \widetilde{\textsf{t}}))} \end{aligned}$$

(46a)

$$\begin{aligned} T &\equiv {} \exists x \bigl [ cube (x) \wedge \underbrace{ large ( cube ) (x) }_{\text {by predicate modification}} \bigr ] \mathrel {\Rightarrow }{} \dots \end{aligned}$$

(46b)

$$\begin{aligned} & \mathrel {\Rightarrow }{} \exists x \bigl [ (c_{1} \wedge l) \mathrel {\textsf{where}}\{\, c_{1} \mathrel {\mathop :}= cube (x), \, l \mathrel {\mathop :}= large (c_{2}) (x), \, c_{2} \mathrel {\mathop :}= cube \,\} \bigr ] \end{aligned}$$

(46c)

$$\begin{aligned} & \qquad \qquad \qquad \qquad \qquad \qquad \qquad \ \text {ab}\text { to }\wedge ; \text {(lq-comp), (B-S)} \nonumber \\ & \mathrel {\Rightarrow }{} \exists x \underbrace{ (c'_{1}(x) \wedge l'(x)) }_{T_{0} } \mathrel {\textsf{where}}\{\, c'_{1} \mathrel {\mathop :}=\lambda (x) ( cube (x)), \, \end{aligned}$$

(46d)

$$\begin{aligned} &\qquad \quad \ \ l' \mathrel {\mathop :}=\lambda (x) ( large (c'_{2}(x)) (x)), \, c'_{2} \mathrel {\mathop :}=\lambda (x) cube \,\} \end{aligned}$$

(46e)

$$\begin{aligned} & \qquad \qquad \qquad \ \text {(46d)}-\text {(46e)}\text { is by }(\xi )\text { on }\text {(46c)}\text { for }\exists \nonumber \\ & \mathrel {\Rightarrow _{\gamma ^*}}{} \exists x (c'_{1}(x) \wedge l'(x)) \mathrel {\textsf{where}}\{\, c'_{1} \mathrel {\mathop :}=\lambda (x) ( cube (x)), \, \end{aligned}$$

(46f)

$$\begin{aligned} &\qquad \quad \ l' \mathrel {\mathop :}=\lambda (x) ( large (c_{2}) (x)), \, c_{2} \mathrel {\mathop :}= cube \,\} \end{aligned}$$

(46g)

$$\begin{aligned} &\equiv {} \textsf{cf}_{\gamma ^*}(T) \qquad \qquad \qquad \text {by }(\gamma ^*)\text { rule to }c'_{2}(x)\text { for }c'_{2} \mathrel {\mathop :}=\lambda (x) cube \nonumber \\ &\approx {} \exists x (c'_{1}(x) \wedge l'(x)) \mathrel {\textsf{where}}\{\, c'_{1} \mathrel {\mathop :}= cube , \, \end{aligned}$$

(46h)

$$\begin{aligned} &\qquad \quad \ l' \mathrel {\mathop :}=\lambda (x) ( large (c_{2}) (x)), \, c_{2} \mathrel {\mathop :}= cube \,\} \end{aligned}$$

(46i)

Proposition 1

The $\text {L}^{\lambda }_{\text {ar}}$-terms $C \approx \textsf{cf}(C)$ in (47a)–(47e), similarly to many other $\text {L}^{\lambda }_{\text {ar}}$-terms, are not algorithmically equivalent to any explicit term.

Therefore, $\text {L}^{\lambda }_{\text {ar}}$ ($\text {L}^{\lambda }_{r}$) is a strict, proper extension of Gallin $\textrm{TY}_2$.

Proof

It follows from (47a)–(47e), by Theorem 2, (2), since $c'$ occurs in two parts of $\textsf{cf}(C)$ in (47e):

$$\begin{aligned} &\text {Some cube is large} \xrightarrow {\textsf{render}}{} C \end{aligned}$$

(47a)

$$\begin{aligned} C & \equiv {} \underbrace{ \exists x \bigl [ c'(x) \wedge large (c') (x) \bigr ] }_{E_{0}} \mathrel {\textsf{where}}\{\, c' \mathrel {\mathop :}= cube \,\} \end{aligned}$$

(47b)

$$\begin{aligned} & \mathrel {\Rightarrow }{} \underbrace{ \exists x \bigl [ \bigl ( c'(x) \wedge l \bigr ) \mathrel {\textsf{where}}\{\, l \mathrel {\mathop :}= large (c') (x) \,\} \bigr ] }_{E_{1}} \mathrel {\textsf{where}}\{\, c' \mathrel {\mathop :}= cube \,\} \end{aligned}$$

(47c)

$$\begin{aligned} & \qquad \quad \ \text {from }\text {(47b)},\text { by }\text {(ap)}\text { to }\wedge \text { of }E_{0}; \text {(lq-comp)}\text { of }\exists ; \text {(rec-comp)} \nonumber \\ &\begin{aligned} & \mathrel {\Rightarrow }{} \bigl [ \underbrace{ \exists x \bigl ( c'(x) \wedge l' (x) \bigr ) \mathrel {\textsf{where}}\{\, l' \mathrel {\mathop :}=\lambda (x) \bigl ( large (c') (x) \bigr ) \,\} }_{E_{2}} \bigr ] \mathrel {\textsf{where}}\{\, \\ &\qquad \qquad \ \ c' \mathrel {\mathop :}= cube \,\} \qquad \qquad \text {from }\text {(47c)},\text { by }(\xi )\text {to}\exists \end{aligned} \end{aligned}$$

(47d)

$$\begin{aligned} & \mathrel {\Rightarrow }{} \underbrace{ \exists x \bigl ( c'(x) \wedge l' (x) \bigr ) }_{C_{0}: \text { an algorithmic pattern} } \mathrel {\textsf{where}}\{\, \underbrace{ c' \mathrel {\mathop :}= cube , \ l' \mathrel {\mathop :}=\lambda (x) \bigl ( large (c') (x) \bigr ) }_{\text {instantiations of memory }c', l' } \,\} \nonumber \\ & \equiv {} \textsf{cf}(C) \quad \text { from }\text {(47d)},\text { by }\text {(head); (cong)}\text { of reordering assignments} \end{aligned}$$

(47e)

5 Expressiveness of $\text {L}^{\lambda }_{\text {ar}}$ for Coordination in Natural Language Phrases

5.1 Coordinated Predication Versus Sentential Conjunction

In this paper, we have extended the algorithmic expressiveness of $\text {L}^{\lambda }_{\text {ar}}$.

We demonstrate it by comparing natural language sentences and their renderings into $\text {L}^{\lambda }_{\text {ar}}$ recursion terms, which express their algorithmic meanings, e.g., (49c)–(49d) and (50j)–(50k). The canonical forms $\textsf{cf}(A)$ in (49c)–(49d) and (50j)–(50k) are denotationally and algorithmically equivalent to the $\lambda$-calculus term A in (49b) and (50a).

In addition, there are $\text {L}^{\lambda }_{\text {ar}}$ recursion terms that are not algorithmically equivalent to any $\lambda$-calculi terms, see (A)–(C), Proposition 2, and also Sect. 6.

Coordinated Predication: a class of sentences with coordinated VPs

$$\begin{aligned} &[\varPhi _{j}]_{{\textsc {np}}} \ \bigl [ [ \varTheta _{L} \text { and } \varPsi _{H}] \ [W_{w}]_{{\textsc {np}}} \bigr ]_{{\textsc {vp}}} \xrightarrow {\textsf{render}}{} A_{0} \end{aligned}$$

(48a)

$$\begin{aligned} A_{0} &\equiv {} \underbrace{ \lambda x_j \bigl [ \lambda y_w \, \big (L (x_j) (y_w) \wedge H(x_j) (y_w) \big ) (w) \bigr ] (j) }_{\text {algorithmic pattern with memory parameters }L, H, w, j} \end{aligned}$$

(48b)

Specific Instantiations of Parametric Algorithms, e.g., (48a)–(48b) and (49c), by (49d):

$$\begin{aligned} &\text {[John]}_j\text { loves and honors [his]}_j\text { wife.} \xrightarrow {\textsf{render}}A \end{aligned}$$

(49a)

$$\begin{aligned} A \equiv {}& \lambda x_j \bigl [\lambda y_w \bigl ( loves (y_w)(x_j) \wedge honors (y_w)(x_j) \bigr ) ( wife (x_j)) \bigr ] ( john ) \end{aligned}$$

(49b)

$$\begin{aligned} \mathrel {\Rightarrow }{}& \dots \mathrel {\Rightarrow }{} \textsf{cf}(A) \equiv {} \underbrace{ \lambda x_j \bigl [ \lambda y_w \, \big (L'' (x_j) (y_w) \wedge H'' (x_j) (y_w) \big ) (w' (x_j)) \bigr ] (j) }_{\text {algorithmic pattern with memory parameters }L'', H'', w', j} \end{aligned}$$

(49c)

$$\begin{aligned} & \qquad \qquad \mathrel {\textsf{where}}{} \{\, L'' \mathrel {\mathop :}=\lambda x_j \lambda y_w \, loves (y_w)(x_j), \, \nonumber \\ &\qquad \qquad \qquad \quad \ H'' \mathrel {\mathop :}=\lambda x_j \lambda y_w \, honors (y_w)(x_j), \,\nonumber \\ & \qquad \qquad \qquad \quad \underbrace{\quad w' \mathrel {\mathop :}=\lambda x_j wife (x_j), \, j \mathrel {\mathop :}= john }_{\text {instantiations of memory }L'', H'', w', j } \, \} \end{aligned}$$

(49d)

The predication by the sentence (49a) is expressed denotationally by the rendering term A in (49b). The algorithm for computing its denotation $\textsf{den}(A)$ in $\text {L}^{\lambda }_{\text {ar}}$, is determined by its canonical form $\textsf{cf}(A)$ (49c)–(49d).

Reduction of Coordinated Relation to Canonical Form. A reduction of the predication term A in (49b) to its canonical form $\textsf{cf}(A)$ (49c)–(49d) is provided by (50a)–(50j):

In contrast to (49a)–(49b), the propositional content of the sentence in (51a), which is a predicative conjunction, can be represented by the following recursion terms (51b)–(51c) of $\text {L}^{\lambda }_{\text {ar}}$. The terms in (51b)–(51c) are algorithmically equivalent (synonymous), by the reduction calculus of $\text {L}^{\lambda }_{\text {ar}}$, and their head parts are conjunction propositions, which is expressed by the sentence (51a) too:

$$\begin{aligned} &\text {[John]}_j\text { loves [[his]}_j\text { wife]}_w \text { and [he]}_j\text { honors [her]}_w \end{aligned}$$

(51a)

$$\begin{aligned} \xrightarrow {\textsf{render}}_{{\textsf {co}\hbox {-}\textsf {index}}_{ar}} \ {} &\bigl [ love (w)(j) \wedge honors (w)(j) \bigr ] \, \mathrel {\textsf{where}}\, \{\, \nonumber \\ & \qquad \qquad \qquad \quad \ j \mathrel {\mathop :}= john , \, w \mathrel {\mathop :}= wife (j) \,\} \end{aligned}$$

(51b)

$$\begin{aligned} \mathrel {\Rightarrow _{\textsf{cf}_{\gamma ^*}}}{} &\bigl [ L \wedge H \bigr ] \, \mathrel {\textsf{where}}\, \{ L \mathrel {\mathop :}= love (w)(j), \, H \mathrel {\mathop :}= honors (w)(j), \, \nonumber \\ &\qquad \qquad \qquad \quad \ j \mathrel {\mathop :}= john , \, w \mathrel {\mathop :}= wife (j) \,\} \end{aligned}$$

(51c)

Proposition 2

• (1) The terms in the reduction sequence (50a)–(50j) are all algorithmically equivalent with each other and with (50k)

• (2) The terms in (50a)–(50j), (50k) are not algorithmically equivalent with the ones in (51b)–(51c)

• (3) The terms (51b)–(51c) are not algorithmically equivalent to any explicit $\text {L}^{\lambda }_{\text {ar}}$, which are $\lambda$-calculus, i.e., Gallin $\textrm{TY}_2$ terms (see (A)–(C) on page 5)

• (4) The terms (51b)–(51c) are not algorithmically equivalent to any $\lambda$-calculus terms that are interpreted IL terms into $\textrm{TY}_2$

Proof

(1)–(2) follow directly from Definition 14 and (43a)–(43b). (3)–(4) follow from Theorem 2, and also from Theorem §3.24 in  [18]. This is because there is a recursion variable (i.e., two, j and w) occurring in more than one part of the $\gamma ^{*}$-canonical form (51c).    $\square$

6 Some Relations Between Let-Expressions and Recursion Terms

Scott [21] introduced the let-expressions by the LCF language of $\lambda$-calculus, which has been implemented by the functional programming languages, e.g., ML, see e.g., Milner [13], Scheme,², Haskell,³ e.g., see Marlow [12], OCaml, etc. Classic imperative languages, e.g., ALGOL and Pascal, implement let-expressions for the scope of functions in their definitions.

A lambda calculus with a formal language that includes terms of let-binding is presented by Nishizaki [19]. A constant $\mathrel {\textsf{where}}$ is used in the formation of terms in Landin [2], which are similar to let-expressions.

The formal language of full recursion $\text {L}^{\lambda }_{r}$, see Definition 1, (3a)–(3d), without the acyclicity (AC), is an extension of the language LCF introduced by Plotkin [20]. The $\lambda$-calculus of LCF has been having a grounding significance in Computer Science, for the distinctions between denotational and operational semantics.

Details of possible similarities and differences between let-expressions in $\lambda$-calculus, and the recursion $\text {L}^{\lambda }_{\text {ar}}$ terms of the form (3d) ($n \ge 1$), in Definition. 1, need carefull representation, which is not in the scope of the work.

In this section, we show that, in general, the recursion $\text {L}^{\lambda }_{\text {ar}}$ terms diverge from the standard let-expressions, in the sense that the reduction calculi of $\text {L}^{\lambda }_{\text {ar}}$ provide algorithmic meanings of the $\text {L}^{\lambda }_{\text {ar}}$ terms via their canonical forms $\textsf{cf}(A)$ and $\textsf{cf}_{\gamma ^*}(A)$, and the $\gamma ^*$-Canonical Form Theorem 1.

The algorithmic semantics by $\text {L}^{\lambda }_{\text {ar}}$ and $\text {L}^{\lambda }_{r}$ is provided by the reduction system, which includes, very importantly, division of the variables into two kinds, proper and recursion, and also of terms as either immediate or proper. Recursion variables $p \in \textsf{RecV}$ are for assignments in the scope of the $\mathrel {\textsf{where}}$ operator. They can not be used for $\lambda$-abstraction, which uses pure variables. To have a correspondence of a recursion term A, e.g. as in (53a), with a let-expression via a sequence of characteristic $\lambda$-abstractions, as in (52a), we can use one-to-one, bijective replacements with fresh pure variables, as in (54a).

The $\lambda$-terms of the form in (52a) are characteristic for the values of the corresponding let-expressions, and can be used as a defining representation of let-expressions:

$$\begin{aligned} & \textsf {let}\; x_{1}=D_{1},\dots ,x_{n}=D_{n}\, \textsf {in}\, D_{0} \equiv \lambda (x_{1}) \bigl ( \dots [\lambda (x_{n}) (D_{0})] (D_{n}) \dots \bigr ) (D_{1}) \end{aligned}$$

(52a)

$$\begin{aligned} & \text {if }x_{j} \in \textsf{FreeV}(D_{i}),\text { then }j < i, \text { i.e., } \textsf{den}(D_i)\text { may depend on } \textsf{den}(x_{j}) \end{aligned}$$

(52b)

Assume that $A \in {\textsf{Terms}}$ is a $\text {L}^{\lambda }_{\text {ar}}$ term of the form (53a), for some $A_{j}\in {\textsf{Terms}}$, $j \in \{0, \dots , n\}$, such that:

• (1) $A_{j}$ has no occurrences of recursion (memory) variables that are different from $p_{i} \in \textsf{RecV}$, $i \in \{1, \dots , n\}$

• (2) $\textsf{rank}$ is such that (53b) holds

$$\begin{aligned} A &\equiv \textsf{cf}_{\gamma ^*}(A) \equiv A_0 \mathrel {\textsf{where}}\{p_1 \mathrel {\mathop :}=A_1, \ldots , p_n \mathrel {\mathop :}=A_n\} \end{aligned}$$

(53a)

$$\begin{aligned} &\textsf{rank}(p_{i}) = i, \ \text {for }i \in \{1, \dots , n\} \end{aligned}$$

(53b)

Note: It can be proved that, for each $\text {L}^{\lambda }_{\text {ar}}$ term (3d), Definition 1, there is at least one such $\textsf{rank}$, see [6]. For any i, j, such that $j < i$, it is not required that $p_{j} \in \textsf{FreeV}(A_{i})$, but this is possible, even for more than one i, see Theorem 2, sentences like (51a) and terms (51b)–(51c).

For the purpose of the demonstration in this section, we introduce specific let-expressions, by the abbreviations (54a)–(54b). We focus on the special case of $n=1$, (56), in the rest of this section.

$$\begin{aligned} & \textsf {let}\; x_{1}=D_{1},\dots ,x_{n}=D_{n}\, \textsf {in}\, D_{0} \end{aligned}$$

(54a)

$$\begin{aligned} \equiv {} & \lambda (x_{1}) \bigl ( \dots [\lambda (x_{n}) (D_{0})] (D_{n}) \dots \bigr ) (D_{1}) \nonumber \\ & x_{i} \in \textsf{PureV}_{\tau _{i}}, x_{i} \not \in \textsf{Vars}(A), n\ge 1, \ \text {for }i \in \{1, \dots , n\} \nonumber \\ D_{j} \equiv {}& A_{j}\{p_{1} \mathrel {\mathop :}\equiv x_{1}, \dots , p_{n} \mathrel {\mathop :}\equiv x_{n} \}, \ \text {for }j \in \{0, \dots , n\} \end{aligned}$$

(54b)

In the special case of $n=1$, with just one assignment: :

$$\begin{aligned} A &\equiv \textsf{cf}_{\gamma ^*}(A) \equiv A_0 \mathrel {\textsf{where}}\{p_1 \mathrel {\mathop :}=A_1\}, \quad p_{1} \not \in \textsf{Vars}(A_{1})\text { for acyclicity} \end{aligned}$$

(55)

$$\begin{aligned} & \textsf {let}\; x_{1}=A_{1}\, \textsf {in}\, A_{0}\{p_{1} \mathrel {\mathop :}\equiv x_{1} \} \equiv \lambda (x_{1}) \bigl ( A_{0}\{p_{1} \mathrel {\mathop :}\equiv x_{1} \} \bigr ) (A_{1}) \end{aligned}$$

(56)

When replacing a memory variable $p \in \textsf{RecV}$ with a pure variable $x \in \textsf{PureV}$, in an explicit, irreducible term A, the result can be reducible term, by (ab). When an immediate term of the form $\lambda (\overrightarrow{u}) p (\overrightarrow{v})$, for $(\textsf{lgh}( \overrightarrow{u} ) + \textsf{lgh}( \overrightarrow{v} ) ) \ge 1$, e.g., p(u), $\lambda (v)p$, $\lambda (v)p(u)$, etc., occurs in an argument position of A. After replacement, $\lambda (\overrightarrow{u}) x (\overrightarrow{v})$ is not an immediate term, by Definition 4.

Lemma 3

Assume that $C \in {\textsf{Terms}}$ is explicit, irreducible, such that (1)–(2):

• (1) $p_{1} \in \textsf{RecV}_{\tau _{1}}$, $\overrightarrow{u}, \overrightarrow{v}, z \in \textsf{PureV}$, such that $(\textsf{lgh}( \overrightarrow{u} ) + \textsf{lgh}( \overrightarrow{v} ) ) \ge 1$

• (2) $p_{1} \not \in \textsf{FreeV}(C)$

Let $A_{0} \equiv \lambda (z) \bigl [ C\bigl (\lambda (\overrightarrow{u}) p_{1} (\overrightarrow{v}) \bigr ) \bigr ]$. Let $x_{1} \in \textsf{PureV}_{\tau _{1}}$ and $x_{1}$ be fresh for $A_{0}$, i.e., $x_{1} \not \in \textsf{Vars}(A_{0})$. Then:

$$\begin{aligned} &C(\lambda (\overrightarrow{u}) p_{1} (\overrightarrow{v})) \text { and } A_{0} \equiv \lambda (z) \bigl [ C\bigl (\lambda (\overrightarrow{u}) p_{1} (\overrightarrow{v}) \bigr ) \bigr ] \text { are explicit, irreducible} \end{aligned}$$

(57a)

$$\begin{aligned} &[C(\lambda (\overrightarrow{u}) p_{1} (\overrightarrow{v}))] \{p_{1} \mathrel {\mathop :}\equiv x_{1} \} \text { and }A_{0}\text { are reducible} \end{aligned}$$

(57b)

Proof

By (2), $C \{p_{1} \mathrel {\mathop :}\equiv x_{1} \} \equiv C$. The following reductions can be done:

$$\begin{aligned} & [C(\lambda (\overrightarrow{u}) p_{1} (\overrightarrow{v})) ] \{p_{1} \mathrel {\mathop :}\equiv x_{1} \} \equiv {} C(\lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v})) \end{aligned}$$

(58a)

$$\begin{aligned} \mathrel {\Rightarrow }{}& C(r_{1}) \mathrel {\textsf{where}}\{\, r_{1} \mathrel {\mathop :}=\lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v}) \,\} \qquad \qquad \ \text { by }\hbox {(ap)} \text { from } \text {(58a)} \end{aligned}$$

(58b)

Then:

$$\begin{aligned} & \begin{aligned} &A_{0}\{p_{1} \mathrel {\mathop :}\equiv x_{1} \} \equiv {} \lambda (z) \bigl [ C\bigl (\lambda (\overrightarrow{u}) p_{1} (\overrightarrow{v}) \bigr ) \bigr ] \{p_{1} \mathrel {\mathop :}\equiv x_{1} \} \\ &\equiv {} \lambda (z) \bigl [ C\bigl (\lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v}) \bigr ) \bigr ] \end{aligned} \end{aligned}$$

(59a)

$$\begin{aligned} &\mathrel {\Rightarrow }{} \lambda (z) \bigl [ C(r_{1}) \mathrel {\textsf{where}}\{\, r_{1} \mathrel {\mathop :}=\lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v})\,\} \bigr ] \qquad \qquad \text { by }\hbox {(ap), (lq-comp)} \end{aligned}$$

(59b)

$$\begin{aligned} &\mathrel {\Rightarrow }{} \lambda (z) \bigl [ C(r'_{1}(z)) \bigr ] \mathrel {\textsf{where}}\{\, r'_{1} \mathrel {\mathop :}=\lambda (z) \lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v}) \,\} \equiv {} A'_{0} \ \text { by }(\xi )\ \text {for }\lambda (z) \end{aligned}$$

(59c)

There are two cases:

Case 1$z \in \textsf{FreeV}(\lambda (\overrightarrow{u}) p_{1} (\overrightarrow{v}))$. Then $A_{0}\{p_{1} \mathrel {\mathop :}\equiv x_{1} \} \mathrel {\Rightarrow }{} A'_{0} \equiv {} \textsf{cf}_{\gamma ^*}(A'_{0})$.

Case 2$z \not \in \textsf{FreeV}(\lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v}))$. Then:

$$\begin{aligned} &A'_{0} \mathrel {\Rightarrow _{(\gamma ^*)}}{} \lambda (z) \bigl [ C(r_{1}) \bigr ] \mathrel {\textsf{where}}\{\, r_{1} \mathrel {\mathop :}=\lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v}) \,\} \equiv {} \textsf{cf}_{\gamma ^*}(A'_{0}) \ \ \, \text { by } (\gamma ^*) \end{aligned}$$

(60a)

$$\begin{aligned} & A_{0}\{p_{1} \mathrel {\mathop :}\equiv x_{1} \} \mathrel {\Rightarrow }{} A'_{0} \mathrel {\Rightarrow _{\gamma ^*}}\textsf{cf}_{\gamma ^*}(A'_{0}) \end{aligned}$$

(60b)

   $\square$

Lemma 4

Assume that $A \in {\textsf{Terms}}$ is as in (61), with the variables as in Lemma 3, Case 2, i.e., $p_{1} \in \textsf{RecV}_{\tau _{1}}$, $\overrightarrow{u}, \overrightarrow{v}, z \in \textsf{PureV}$, for explicit, irreducible $C, A_{1} \in {\textsf{Terms}}$, such that $A_{1}$ is proper, and $p_{1} \not \in \textsf{FreeV}(C)$ ($p_{1} \not \in \textsf{FreeV}(A_{1})$ by acyclicity), $x_{1} \in \textsf{PureV}_{\tau _{1}}$, $x_{1} \not \in \textsf{Vars}(A)$, and $z \not \in \textsf{FreeV}(\lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v}))$:

$$\begin{aligned} A \equiv \textsf{cf}_{\gamma ^*}(A) \equiv {} & \underbrace{ \lambda (z) \bigl [ C\bigl (\lambda (\overrightarrow{u}) p_{1} (\overrightarrow{v}) \bigr ) \bigr ] }_{A_{0}} \mathrel {\textsf{where}}\{\, p_{1} \mathrel {\mathop :}=A_{1} \,\} \end{aligned}$$

(61)

Then, the conversion of the assignment in A into a $\lambda$-abstract over $A_{0}$, applied to $A_{1}$, results in a term, which is not algorithmically equivalent to A (similarly, for Case 1):

(62)

Proof

$$\begin{aligned} A' &\equiv {} \bigl [ \lambda (x_{1}) \bigl ( A_{0}\{p_{1} \mathrel {\mathop :}\equiv x_{1} \} \bigr ) \bigr ] (A_{1}) \end{aligned}$$

(63a)

$$\begin{aligned} &\equiv {} \lambda (x_{1}) \Bigl [ \bigl [ \underbrace{ \lambda (z) \bigl [ C\bigl (\lambda (\overrightarrow{u}) p_{1} (\overrightarrow{v}) \bigr ) \bigr ] }_{A_{0}} \bigr ] \{p_{1} \mathrel {\mathop :}\equiv x_{1} \} \Bigr ] (A_{1}) \end{aligned}$$

(63b)

$$\begin{aligned} &\mathrel {\Rightarrow }{} \lambda (x_{1}) \Bigl [ \lambda (z) \bigl [ C(r_{1}) \bigr ] \mathrel {\textsf{where}}\{\, r_{1} \mathrel {\mathop :}=\lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v}) \,\} \Bigr ] (A_{1}) \end{aligned}$$

(63c)

$$\begin{aligned} &\qquad \ \text {by }\text {(60a), (lq-comp), (ap-comp)} \nonumber \\ &\mathrel {\Rightarrow }{} \Bigl [ \lambda (x_{1}) \bigl [ \lambda (z) \bigl [ C(r^{1}_{1}(x_{1})) \bigr ] \bigl ] \mathrel {\textsf{where}}\{\, r^{1}_{1} \mathrel {\mathop :}=\lambda (x_{1}) \lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v}) \,\} \Bigr ] (A_{1}) \end{aligned}$$

(63d)

$$\begin{aligned} &\qquad \ \ \text { by } (\xi ) \text { for } \lambda (x_{1}), \text {(ap-comp)} \nonumber \\ &\mathrel {\Rightarrow }{} \lambda (x_{1}) \bigl [ \lambda (z) \bigl [ C(r^{1}_{1}(x_{1})) \bigr ] \bigl ] (A_{1}) \mathrel {\textsf{where}}\{\, r^{1}_{1} \mathrel {\mathop :}=\lambda (x_{1}) \lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v}) \,\} \end{aligned}$$

(63e)

$$\begin{aligned} &\qquad \ \ \text { by }\text {(recap)} \nonumber \\ &\mathrel {\Rightarrow }{} \Bigl [ \lambda (x_{1}) \bigl [ \lambda (z) \bigl [ C(r^{1}_{1}(x_{1})) \bigr ] \bigl ] (p_{1}) \mathrel {\textsf{where}}\{ p_{1} \mathrel {\mathop :}=A_{1} \} \Bigr ]\nonumber \\ &\qquad \qquad \qquad \qquad \qquad \ \ \ \mathrel {\textsf{where}}\{\, r^{1}_{1} \mathrel {\mathop :}=\lambda (x_{1}) \lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v}) \,\} \end{aligned}$$

(63f)

$$\begin{aligned} &\qquad \ \text { by }\text {(ap), (rec-comp)} \nonumber \\ & \begin{aligned} &\mathrel {\Rightarrow }{} \lambda (x_{1}) \bigl [ \lambda (z) \bigl [ C(r^{1}_{1}(x_{1})) \bigr ] \bigl ] (p_{1}) \mathrel {\textsf{where}}\\ &\qquad \ \ \{ p_{1} \mathrel {\mathop :}=A_{1}, \ r^{1}_{1} \mathrel {\mathop :}=\lambda (x_{1}) \lambda (\overrightarrow{u}) x_{1} (\overrightarrow{v}) \,\} \equiv \textsf{cf}_{\gamma ^*}(A') \end{aligned} \ \text { by }\text {(head)} \end{aligned}$$

(63g)

Thus, (62) holds: A and $A'$ are not algorithmically equivalent, , which follows, by Definition 14, from (61) and (63g). (Similarly, for Case 1.)    $\square$

Proposition 3

In general, the algorithmic equivalence does not hold between the $\text {L}^{\lambda }_{\text {ar}}$ recursion terms of the form (53a) and the $\lambda$-calculus terms (54a)–(54b), which are characteristic for the corresponding let-expressions in $\lambda$-calculus.

Proof

By Lemma 4, the special set of terms in it provide counterexamples to alleged algorithmic equality between all terms in (53a) and (54a)–(54b).    $\square$

The let-expressions, represented by the specific, characteristic $\lambda$-terms (54a)–(54b) in $\text {L}^{\lambda }_{\text {ar}}$, are only denotationally equivalent to the corresponding recursion terms, but not algorithmically in the most significant cases. The full proofs are the subject of forthcoming papers.

7 Conclusion and Outlook for Future Work

In this paper, I have presented some of the major characteristics of $\text {L}^{\lambda }_{\text {ar}}$, by also developing it for enhancing its mathematical capacities for logic, theoretically, by targeting applications.

Algorithmic Semantics: The essential theoretic features of $\text {L}^{\lambda }_{\text {ar}}$ provide algorithmic semantics of formal and natural languages. Computational semantics by $\text {L}^{\lambda }_{\text {ar}}$ has the fundamental distinction between algorithmic and denotational semantics. The algorithms determined by terms in canonical forms compute their denotations, see Fig. 1.

While the theory has already been quite well developed, with eyes towards versatile applications, it is an open subject with many open and ongoing tasks and perspectives. The greater semantic distinctions of the formal language and calculi of $\text {L}^{\lambda }_{\text {ar}}$ enhance type-theoretic semantics by traditional $\lambda$-calculi. I have demonstrated that, by being a strict extension of Gallin $\textrm{TY}_2$ [1], $\text {L}^{\lambda }_{\text {ar}}$ exceeds also the facilities of Montague [14] IL, e.g., see Sect. 4, Propositions 1–2.

Algorithmic Patterns for Computational Semantics: Memory locations, i.e., recursion variables in $\text {L}^{\lambda }_{\text {ar}}$ terms represent parameters that can be instantiated by corresponding canonical forms, depending on context, the specific areas of applications, and domain specific texts, e.g., as in (45c) and (47d); and (48a)–(48b), as in (50k).

Logical Constants and Quantifiers in $\text {L}^{\lambda }_{\text {ar}}$: Canonical forms can be used for reasoning and inferences of semantic information by automatic provers and proof assistants. This is a subject of future work.