Numerical Simulations of the Lorentz Force Effect on Thermal Convection in an Inclined Square Cavity Filled with a Non-Newtonian Fluid

Abstract

The authors examine the influence of a uniform magnetic field on the characteristics of thermal and dynamic behaviors of non-Newtonian fluid generated by natural convection in a tilted square cavity. The MRT-LBM is employed to elucidate the main physical parameters’ effect, namely, the Hartmann number $Ha$ (from 0 to 50) and the power-law index $n$ (from 0.6 to 1.4), for fixed inclination angle ($\gamma = 45^\circ$) and Rayleigh number ($Ra = 10^{5}$). According to the findings of this study, the flow intensity and the heat transfer are negatively affected by rising either the power-law index or the Hartmann number.

1 Introduction

The heat transfer generated by natural convection in enclosures is one of the main topics of interest due to its involvement in various practical and industrial applications, including, among others, biomedical, chemical, and textile industries. Furthermore, the study of the thermal and dynamic behaviors of a non-Newtonian fluid is complicated by the fact that the shear stress variation with respect to shear rate is non-linear. Commonly, non-Newtonian liquids behave as shear-thickening/(shear-thinning) fluids when their viscosities increase/(drop) with the shear rate.

The literature review shows that numerous studies have been published on fluid flows with specific rheological behaviors, generated by natural convection. The numerical investigation by Kim et al. [1] was conducted on free convection in an enclosure differentially heated and confining a fluid with rheological behavior using the FVM (Finite Volume Method). Their findings show that the flow intensity rises, and the heat transfer is improved by reducing the power-law index of the working fluid. Heat transfer generated by free convection of non-Newtonian fluid in a rectangular enclosure subjected to heating from below by imposing a uniform heat flux was conducted by Lamsaadi et al. [2]. They demonstrated that an approximate analytical solution is feasible for fluids with complex rheological behaviors in such conditions. In another study, Lamsaadi et al. [3] carried out a numerical and theoretical investigation of free convection heat transfer of non-Newtonian fluids in an inclined enclosure subjected to uniform heating. They reported that the cavity’s inclination has a considerable influence on the heat transfer exchanged between the fluid and the active walls of the enclosure. As well, the flow structure and particularly its intensity are visibly dependent on the rheological behavior. Turan et al. [4] used the commercial code FLUENT to study the heat transfer generated by free convection in a differentially heated square cavity and confining a power-law non-Newtonian fluid. They observed that the Nusselt number is negatively affected by the increase of the power law index. More recently, Daghab et al. [5] employed the FVM to investigate natural convection in a square cavity submitted to a destabilizing heat flux from the bottom while its vertical sides were maintained isothermally cold. The non-Newtonian working fluid was thermo-dependent. Their results show that the cooling performance is upgraded by raising the Rayleigh and Pearson numbers and declining the power-law index.

The presence of a Lorentz force acts by controlling the heat transfer generated by convection. In this context, Makayssi et al. [6] employed the FDM (Finite Difference Method) to investigate thermosolutal natural convection in a square enclosure filled with a non-Newtonian fluid and subject to the effect of a tilted magnetic field. Their findings show a significant influence of the tilted magnetic field and its intensity on the resulting heat and mass transfers.

Nowadays, the lattice-Boltzmann method (LBM) is among the most widely used numerical methods for dealing with non-Newtonian flows. This mesoscopic method offers many benefits, such as the ease of calculating the local shear rate, its ease adaptability to parallel computing, and the ease of implementing boundary conditions on complex geometries [7]. The flow of a non-Newtonian fluid driven by two facing lids has been studied using the basic lattice-Boltzmann relaxation approach [8]. Kefayati et al. [9] used a hybrid FD-LBM technique to investigate the combined effects of natural convection and magnetic field on the dynamic and thermal behaviors of a non-Newtonian fluid. Recently, the MRT-LBM has been used to investigate the flow of non-Newtonian fluids in cavities [10, 11].

According to this preliminary bibliographic research, natural convection flows of rheological fluids in inclined cavities under the Lorentz force effect are still poorly documented when using the lattice Boltzmann method as a simulation tool. Thus, the goal of the present study consists to quantify the magnetic field impact on the heat transfer generated by natural convection in a tilted square cavity filled with non-Newtonian fluid.

2 Mathematical Formulation

2.1 Physical Model

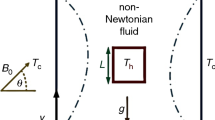
A schematic of the studied 2D physical model is shown in Fig. 1. It is a square cavity, of size $L \times L$, inclined at 45° with respect to the horizontal, with two opposite walls maintained isothermally at different temperatures while the remaining ones are kept insulated. The cavity is filled with a non-Newtonian fluid under the action of an external magnetic field that is maintained parallel to the active walls. The fluid flow is laminar and incompressible, and all the fluid's thermophysical properties are presumed constant, except the density in the buoyancy term that is subject to the Boussinesq approximation.

Fig. 1.

Schematic of the physical model.

2.2 Lattice Boltzmann Method

The MRT lattice Boltzmann method has been used in this study for its stability and many other inherent advantages. To solve the flow field, Eq. (1) is used to determine the distribution function, $f_{k}$, in the presence of the external term force, $F$. This equation is expressed as follows [12, 13]:

$$ \begin{aligned} f\left( {\vec{r} + c_{k} \Delta t,t + \Delta t} \right) & = f\left( {\vec{r},t} \right) - M^{ - 1} S\left( {m\left( {\vec{r},t} \right) - m^{eq} \left( {\vec{r},t} \right)} \right) \\ & \quad + M^{ - 1} \left( {{\mathbb{I}} - S/2} \right)F \\ \end{aligned} $$

(1)

where $M^{ - 1}$ is the inverse of the orthogonal passage matrix and $f = (f_{k} |k = 0 - 8)$ is the local distribution function in the direction $k$ and $c_{k}$ is a discrete velocity, which is defined in the D2Q9 model (exemplified in Fig. 1) as follows:

$$ c_{{k{ }}} = \left\{ {\begin{array}{*{20}l} {\left( {0,0} \right)\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\, k = 0,} \\ {\left( {\cos \left[ {\frac{ - \pi }{2}\left( {1 - {\text{k}}} \right)} \right],\sin \left[ {\frac{ - \pi }{2}\left( {1 - {\text{k}}} \right)} \right]} \right)\quad\, k = 1 - 4,} \\ {\sqrt 2 \left( {\cos \left[ {\frac{\pi }{2}\left( {k - \frac{9}{2}} \right)} \right],\sin \left[ {\frac{\pi }{2}\left( {k - \frac{9}{2}} \right)} \right]} \right)\,k = 5 - 8.} \\ \end{array} } \right. $$

(2)

In Eq. (1), $m = (m_{k} |k = 0 - 8)$ and $m^{eq} = (m_{k}^{eq} |k = 0 - 8)$ are the space moments and their corresponding equilibrium space moments, respectively.

$$ \begin{aligned} m^{eq} & = \left( {\rho , - 2\rho + 3\rho \left( {u^{2} + v^{2} } \right),\rho } \right. \\ & \quad \left. { - 3\rho \left( {u^{2} + v^{2} } \right),\rho u, - \rho u,\rho v, - \rho v,\rho u^{2} - \rho v^{2} ,\rho uv} \right) \\ \end{aligned} $$

(3)

In the moment space, the term force $F = (F_{k} |k = 0 - 8)$ is transformed by Eq. (4) as follows [13]:

$$ F = \left\{ {\begin{array}{*{20}l} {F_{0} = 0} \hfill \\ {F_{1} = 6\rho (F_{x} u + F_{y} v)} \hfill \\ {F_{2} = - 6\rho (F_{x} u + F_{y} v)} \hfill \\ {F_{3} = \rho F_{x} } \hfill \\ {F_{4} = - \rho F_{x} } \hfill \\ {F_{5} = \rho F_{x} } \hfill \\ {F_{6} = - \rho F_{x} } \hfill \\ {F_{7} = 2\rho (F_{x} u - F_{y} v)} \hfill \\ {F_{8} = \rho \left( {F_{y} u + F_{x} v} \right)} \hfill \\ \end{array} } \right. $$

(4)

where $F_{x}$ and $F_{y}$ are the external forces applied in the Ox and Oy directions, respectively. These forces are expressed as follows:

$$ \begin{aligned} F_{x} & = {\text{g}}\beta \left( {T - T_{0} } \right){ }\sin \left( \gamma \right) \\ F_{y} & = {\text{g}}\beta \left( {T - T_{0} } \right){ }\cos \left( \gamma \right) - \frac{{Ha^{2} \mu_{0} }}{{L^{2n} \alpha^{1 - n} }}v \\ \end{aligned} $$

(5)

In Eq. (1), the relaxation diagonal matrix, $S$, is defined as $S = diag\left( {S_{0} ,S_{1} , \cdots ,S_{8} } \right)$, whose elements are such that $S_{0} = S_{3} = S_{5} = 1.0$, $S_{1} = S_{2} = 1.4$, $S_{4} = S_{6} = 1.2$ and $S_{7} = S_{8} = 1 / \tau$. The parameter $\tau$ is the relaxation time, related to the viscosity through the Chapmann-Enskog expansion analysis as follows:

$$ \vartheta = c_{s}^{2} \left( {\tau - 0.5} \right) $$

(6)

The apparent kinematic viscosity for a non-Newtonian fluid is locally variable with the shear rate and obtained as follows:

$$ \vartheta = \frac{{\mu_{0} }}{\rho }\left| {\dot{\gamma }} \right|^{n - 1} $$

(7)

With

$$ \left| {\dot{\gamma }} \right| = \sqrt {2S_{\alpha \beta } S_{\alpha \beta } } $$

(8)

where $\mu_{0}$ and $n$ are the consistency index and power-law index, respectively. The parameter $S_{\alpha \beta }$ is the shear stress, evaluated by Eq. (9) in the MRT model [14].

$$ S_{\alpha \beta } = \frac{ - 3}{{2\rho }}\sum c_{\alpha ,i} c_{\beta ,i} \sum M^{ - 1} SM\left( {f - f^{eq} } \right) $$

(9)

The thermo-physical governing parameters of the present study are:

$$ \begin{array}{*{20}c} {Pr = \left( {\mu_{0} /\rho } \right)L^{2 - 2n} /(\alpha^{2 - n} ){ }} \\ {Ra = g\beta \Delta TL^{2n + 1} /\left( {\left( {\mu_{0} /\rho } \right)\alpha^{n} } \right)} \\ {Ha = B_{0} L^{n} \sqrt {\sigma \alpha^{1 - n} /\left( {\mu_{0} } \right)} } \\ \end{array} $$

(10)

In the numerical simulation, the classical Bounce-Back (BB) condition was adopted to evaluate the unknown density distribution functions along the motionless cavity walls. Finally, the macroscopic quantities like density, $\rho$, and velocity, $\vec{u}$, are calculated as follows:

$$ \rho = \mathop \sum \limits_{k = 0}^{8} f_{k} $$

(11)

$$ \rho \vec{u} = \mathop \sum \limits_{k = 0}^{8} f_{k} \vec{c}_{k} + \frac{{\Delta t\vec{F}}}{2} $$

(12)

Similarly to Eq. (1), the equation used to determine the distribution function, $g_{k}$, for temperature in direction k and for a discrete velocity $c_{k}$ in the D2Q5 model (as shown in Fig. 1) is defined as follows [12, 13]:

$$ g\left( {\vec{r} + c_{k} \Delta t,t + \Delta t} \right) = g\left( {\vec{r},t} \right) - N^{ - 1} Q\left( {n\left( {\vec{r},t} \right) - n^{eq} \left( {\vec{r},t} \right)} \right) $$

(13)

where $n$ is the space moments and $n^{eq}$ is their corresponding equilibrium space moments, defined by Eq. (14). The matrix $N$ is the orthogonal passage matrix for the D2Q5 model.

$$ n^{eq} = \left( {T,uT,vT,aT,0} \right) $$

(14)

In Eq. (13), $Q$ is the relaxation diagonal matrix defined as $Q = diag\left( {Q_{0} ,Q_{1} , \cdots ,Q_{4} } \right)$ and the elements $Q_{i}$ ($i = 0$ to $4$) are such that $Q_{0} = Q_{3} = Q_{4} = 1$ and $Q_{1} = Q_{2} = 1 / \left( {10\alpha /\left( {4 + a} \right) + 0.5} \right)$. In the present study, the constant $a$ is set to −2 [15].

To evaluate the distribution functions g in the physical domain (unknown function) along the rigid walls, we used the following relationship:

$$ g_{w,i} = T_{w} - \mathop \sum \limits_{{j = 0,{ }j \ne i}}^{4} g_{w,j} $$

(15)

Finally, the macroscopic temperature is calculated by:

$$ T = \mathop \sum \limits_{k = 0}^{4} g_{k} $$

(16)

The local Nusselt number rated on the hot wall and its mean value are given, respectively, by the following expressions:

$$ Nu_{L} = - \left. {\frac{\partial T}{{\partial Y}}} \right|_{Y = 0} $$

(17)

And

$$ Nu_{m} = \mathop \smallint \limits_{X = 0}^{X = 1} Nu_{L} dX $$

(18)

2.3 Numerical Validation and Grid Size

To check the reliability of the results provided by the present code, several numerical validation tests have been performed to compare the results obtained by our code with those published in previous studies on natural convection of non-Newtonian fluids. Figure 2 shows results of validation in terms of mean Nusselt number compared to those reported by Turan et al. [4] who considered a cavity differentially heated and filled with a non-Newtonian fluid for $Ra = 10^{5}$ and $Pr = 100$. A fair agreement can be seen from Fig. 2 between both results; the maximum relative difference recorded being within 1.38%.

Fig. 2.

Validation in terms of the mean Nusselt number variations versus $n$.

Prior to the numerical simulations, tests have been conducted to evaluate how the results vary by refining the grid size. Table 1 displays the results obtained in terms of $Nu_{m}$ and $\psi_{max}$ for $Ra = 10^{5}$, $Ha = 50$, $\gamma = 45^\circ$, $n = 0.6$ and different grids. The examination of these results shows that the grid 200 × 200 is suitable for carrying out the present study (the deviations were calculated with respect to 240 × 240 nodes).

Table 1. Effect of the grid size in terms of $Nu_{m}$ and $\psi_{max}$ for $Ra = 10^{5}$, $Ha = 50$, $\gamma = 45^\circ$ and $n = 0.6$.

3 Results and Discussion

The effect of the magnetic field ($0 \le Ha \le 50$) and the power-law index ($0.6 \le n \le 1.4$) on thermal and dynamic aspects of the problem is investigated for $Ra = 10^{5}$, $Pr = 100$ and cavity inclination $\gamma = 45^\circ$. The findings are displayed in terms of streamlines, isotherms and mean Nusselt numbers.

3.1 Streamlines and Isotherms

The effect of the parameters $Ha$ and $n$ is exemplified in Fig. 3 in terms of streamlines. Overall, by decreasing $n$ and $Ha$, the influence of convection on the streamlines becomes increasingly relevant. In fact, for $Ha = 0$, the flow intensity is substantially reduced for the shear thickening fluid ($n > 1$) compared to the Newtonian case (reduction by a factor of 2.42 for $n = 1.4$). In contrast, the flow intensity increases by decreasing the power-law index. Note that, in the absence of the magnetic field, the solution is periodic oscillatory below the critical value $n_{c} = 0.61$. These behaviors result probably from the increase/(decrease) of the fluid apparent viscosity with the shear rate in the case of the shear thinning/(shear thickening) fluid. In the presence of the Lorentz force, the shape of the main flow cell undergoes a big qualitative change favoring the break of the inner streamlines into two cells of comparable sizes and intensities for the shear thinning and Newtonian fluids. Quantitatively, the flow intensity for $n = 1.0$/$1.4$ decreases by 76.96%/58.25% when $Ha$ increases from 0 to 50. Moreover, the oscillatory behavior of the flow observed for $n = 0.6$ in the absence of the magnetic field disappears for $Ha = 50$ and the final flow state becomes stationary.

Fig. 3.

Streamlines versus $Ha$ and $n$ for $Ra = 10^{5}$.

Regarding the thermal aspect of the problem, the effect of $Ha$ and $n$ on the isotherms is illustrated in Fig. 4. This figure shows that the distortions of the isotherms observed in the central part of the cavity for the Newtonian and shear thickening fluids are considerably attenuated with a perceptible relaxation of the isotherms near the active walls for $Ha = 50$. The resulting relaxation of the isotherms is due to the attenuation of the flow intensity accompanying this increase in $Ha$.

3.2 Heat Transfer

Figure 5 depicts the combined effect of the Hartmann number ($Ha$) and the power law index ($n$) on the mean Nusselt number ($Nu_{m}$). The latter drops by increasing either $n$ or $Ha$. Furthermore, when $Ha$ increases, the impact of the power-law index is reduced. In fact, the $Nu_{m}$’s downfall resulting from the increase of $Ha$ is drastic for $n = 0.6$ illustrating the shear thinning fluid (it is of about 67.42% by incrementing $Ha$ from 0 to 50). Comparatively, the reduction of $Nu_{m}$ is very limited for $n = 1.4$ and does not exceed 25.88% for the same increase of $Ha$. Finally, these results illustrate well the known damping role of the magnetic field with a rate that depends both on $Ra$ and $n$.

Fig. 4.

Isotherms versus $Ha$ and $n$ for $Ra = 10^{5}$

Fig. 5.

Mean Nusselt number variations versus $Ha$ and $n$ for $Ra = 10^{5}$.

4 Conclusion

The magnetic field influence on the dynamic and thermal behaviors generated by natural convection in a tilted cavity filled with a non-Newtonian fluid has been investigated numerically using the MRT-LBM. The findings of this study indicate that increasing the Hartmann number and the power law index has a significant impact on the qualitative and quantitative aspects of the outcomes. In the absence of the magnetic field, the solution becomes unsteady and periodic below the threshold value $n_{c} = 0.61$. The magnetic field's dampening action is particularly pronounced in the case of shear-thinning fluid. Globally, this damping role is characterized by a drop in the flow intensity and a reduction in the mean Nusselt number by raising the power law index.