Keywords

1 Introduction

There has been considerable interest in studying the occurrence of rogue waves. The concept of rogue waves, introduced by Drapper (1966), can be generated due to both nonlinear and statistical effects and may occur in infinite and finite water depths (Shukla et al., 2006). Based on two-coupled third-order nonlinear Schrödinger equations (NLSE), Roskes (1976) has studied the instability analysis for surface gravity wave in the presence of second wave in deep water. Dhar and Das (1991) have extended that result starting from the fourth-order nonlinear evolution equation. A further extension of that result to include capillarity has been performed by Dhar and Das (1993). Onorato et al. (2006) have established two-coupled nonlinear Schrödinger equations in the case of two nonlinearly interacting wave systems in infinite water depths and traveling in two different directions. Then, they have studied the instability analysis in the case of unidirectional perturbation. That analysis has been extended by Shukla et al. (2006) to obtain the instability growth rate for bidirectional perturbations. Laine Pearson (2010) has discussed the interaction of two weekly nonlinear wave trains for distinct carrier frequencies and traveling in two separate directions, similar to obliquely interacting waves. He has demonstrated that the instability growth rate for more general two-wave trains can be larger than for short crested waves. Kundu et al. (2013) have also established nonlinear evolutions for two gravity wave packets for a finite depth of water and interacting obliquely on the surface of the water. The creation of rogue waves due to modulational instability of two obliquely propagating wave trains has been discussed by Didenkulova (2011), Gramstad and Trulsen (2010), Hjelmervik and Trulsen (2009), Onorato et al. (2010, 2011). All these investigations that the authors above have performed are for gravity waves. Recently, Manna and Dhar have made a paper on two obliquely acting capillary gravity waves in the water of infinite depth (Manna & Dhar, 2021a), and they have obtained the solutions of coupled third-order NLSE in the (x-t) space (Manna & Dhar, 2021b) for the same problem. The present paper deals with three-coupled third-order nonlinear Schrödinger equations for obliquely interacting capillary gravity waves over finite water depth. In this case, two capillary gravity wave trains travel obliquely and form equal angles with the direction of propagation, which is considered as \(x\) axis. Therefore, this paper is an extension of the work made by Kundu et al. (2013) to include capillarity.

2 Fundamental Equations

We consider the free surface in the undisturbed situation as the \(z = 0\) plane, and \(z\) axis is taken vertically upwards. We take two capillary gravity wave packets of wave numbers \(k_{1} , k_{2}\), respectively, which is traveling in the \(xy\) plane. Next, we take \(z = \eta \left( {x,y,t} \right)\) as the equation of the free surface at time \(t\) in the perturbed state. The perturbed velocity potential \(\phi\) satisfies the three-dimensional Laplace equation

$$\nabla^{2} \phi = 0,{\text{in}}\; - d < z < \eta$$
(1)

The boundary conditions for the wave motion are given by

$$\phi_{z} - \eta_{t} = \phi_{x} \eta_{x} + \phi_{y} \eta_{y} ,{\text{at}}\;z = \eta$$
(2)
$$\phi_{t} + g\eta = - \frac{1}{2}\left( {\nabla \phi } \right)^{2} + \frac{{T\left\{ {\eta_{xx} \left( {1 + \eta_{y}^{2} } \right) + \eta_{yy} \left( {1 + \eta_{x}^{2} } \right) - 2\eta_{xy} \eta_{x} \eta_{y} } \right\}}}{{\left( {1 + \eta_{x}^{2} + \eta_{y}^{2} } \right)^{\frac{3}{2}} }},{\text{at}}\;z = \eta$$
(3)

Also

$$\phi_{z} = 0,{\text{at}}\;z = - d,$$
(4)

where \(T\) is the ratio of the surface tension coefficient to the fluid density and \(g\) represents the acceleration due to gravity.

We look for solutions to the above equations in the form

$$Q = Q_{00} + \mathop \sum \limits_{p = 0}^{\infty } \mathop \sum \limits_{q = 0}^{\infty } \left[ {Q_{pq} e^{{i\left( {p\psi_{1} + q\psi_{2} } \right)}} + c.c.} \right],\quad \left( {p = q \ne 0} \right)$$
(5)

in which \(Q\) represents \(\phi\), \(\eta ,\) and \(c.c.\) indicates complex conjugate and \(\psi_{1} = k_{1} x + k_{2} y - \omega t\), \(\psi_{2} = k_{1} x - k_{2} y - \omega t\). In the above \(\phi_{00} , \phi_{pq} , \phi_{pq}^{*}\) are functions of \(z, x_{1} = \epsilon x, y_{1} = \epsilon y\) and \(t_{1} = \epsilon t\); \(\eta_{00} , \eta_{pq} , \eta_{pq}^{*}\) are functions of \(x_{1} , y_{1}\) and \(t_{1}\). Here, \(\epsilon\) denotes the slow ordering parameter. The linear dispersion relation is given by

$$\omega^{2} - gk\mu \left( {1 + s} \right) = 0,$$
(6)

where \(\mu = \tanh kd, k^{2} = k_{1}^{2} + k_{2}^{2}\) and \(s = \frac{{Tk^{2} }}{g}\).

The group velocity of each of the two-wave packets is as follows

$$c_{g} = \frac{{c_{p} }}{{2\mu \left( {1 + s} \right)}}\left\{ {\mu \left( {1 + 3s} \right) + kd\left( {1 - \mu^{2} } \right)\left( {1 + s} \right)} \right\},$$

where \(c_{p} = \omega /k\) represents the phase velocity.

3 Derivation of Evolution Equations

Following Kundu et al. (2013) and making dimensionless the variables by the relations given by

$$\begin{aligned} & \left( {x_{1} , y_{1} , \eta_{10} , \eta_{01} , d} \right) = \left( {kx_{1} , ky_{1} , k\eta_{10} , k\eta_{01} , kd} \right). \\ & t_{1} = \omega t_{1} , \left( {k_{1} ,k_{2} } \right) = \left( {\frac{{k_{1} }}{k},\frac{{k_{2} }}{k}} \right), \tilde{\phi } = \phi_{00}^{\left( 1 \right)} /\frac{\omega }{{k^{2} }}, \\ \end{aligned}$$
(7)

and finally, using the transformation

$$\xi = x_{1} - \overline{{c_{g} }} t_{1} , \eta = y_{1} , \tau = \epsilon t_{1} ,$$
(8)

we obtain the third-order nonlinear evolution equations consisting of three-coupled equations for crossing sea states

$$\begin{aligned} & 2i\frac{{\partial \eta_{10} }}{\partial \tau } + i\delta_{1} k_{2} \frac{{\partial \eta_{10} }}{\partial \eta } + \delta_{2} \left( {k_{1} \frac{\partial }{\partial \xi } + k_{2} \frac{\partial }{\partial \eta }} \right)^{2} \eta_{10} + \delta_{3} \left( {k_{2} \frac{\partial }{\partial \xi } - k_{1} \frac{\partial }{\partial \eta }} \right)^{2} \eta_{10} \\ & \quad = \left( {\mu_{1} \left| {\eta_{10} } \right|^{2} + \mu_{2} \left| {\eta_{01} } \right|^{2} } \right)\eta_{10} + \eta_{10} P_1\tilde{\phi } \\ \end{aligned}$$
(9)
$$\begin{aligned} & 2i\frac{{\partial \eta_{01} }}{\partial \tau } - i\delta_{1} k_{2} \frac{{\partial \eta_{01} }}{\partial \eta } + \delta_{2} \left( {k_{1} \frac{\partial }{\partial \xi } - k_{2} \frac{\partial }{\partial \eta }} \right)^{2} \eta_{01} + \delta_{3} \left( {k_{2} \frac{\partial }{\partial \xi } + k_{1} \frac{\partial }{\partial \eta }} \right)^{2} \eta_{01} \\ & \quad = \left( {\mu_{1} \left| {\eta_{01} } \right|^{2} + \mu_{2} \left| {\eta_{10} } \right|^{2} } \right)\eta_{01} + \eta_{01} P_2\tilde{\phi } \\ \end{aligned}$$
(10)

and

$$\left( {\gamma_{1} \frac{{\partial^{2} }}{{\partial \xi^{2} }} + \gamma_{2} \frac{{\partial^{2} }}{{\partial \eta^{2} }}} \right)\tilde{\phi } = P_1\left| {\eta_{10} } \right|^{2} + P_2\left| {\eta_{01} } \right|^{2} ,$$
(11)

in which the forms of \(P_1, P_2\) are

$$\begin{aligned} & P_1 \equiv \left\{ {2 + \left( {1 - \mu^{2} } \right)\overline{c}_{g} } \right\}k_{1} \frac{\partial }{\partial \xi } + 2k_{2} \frac{\partial }{\partial \eta }, \\ & P_2 \equiv \left\{ {2 + \left( {1 - \mu^{2} } \right)\overline{c}_{g} } \right\}k_{1} \frac{\partial }{\partial \xi } - 2k_{2} \frac{\partial }{\partial \eta }, \\ & \gamma_{1} = k_{1}^{2} \mu^{2} \overline{c}_{g}^{2} - \frac{\mu d}{{1 + s}}, \gamma_{2} = - \frac{\mu d}{{1 + s}}, \\ \end{aligned}$$
(12)

where \(\overline{{c_{g} }} = c_{g} /c_{p}\) and the coefficients of Eqs. (9) and (10) are available in the Appendix. To render the results acceptable, comparing them with other results is useful. For example, in the absence of surface tension, the Eqs. (9) to (11) reduce to the corresponding equations of S. Kundu et al. (2013). Further, for \(s = 0\) and in the limit \(d \to \infty\), the coefficients appearing on the said equations reduce to those of Onorato et al. (2006) and Shukla et al. (2006).

4 Stability Analysis and Results

The solutions of the uniform wave trains are given by

$$\begin{aligned} & \eta_{10} = \alpha_{0} e^{{ - i\tau \Delta \omega_{1} }} \\ & \eta_{01} = \beta_{0} e^{{ - i\tau \Delta \omega_{2} }} , \overline{\phi } = \overline{\phi }_{0} \\ \end{aligned}$$
(13)

in which \(\alpha_{0} , \beta_{0} , \overline{\phi }_{0}\) are real constants, and the frequency shifts due to nonlinearity are

$$2{\Delta }\omega_{1} = \mu_{1} \alpha_{0}^{2} + \mu_{2} \beta_{0}^{2} , 2{\Delta }\omega_{2} = \mu_{1} \beta_{0}^{2} + \mu_{2} \alpha_{0}^{2}$$
(14)

Next, we consider the small perturbations \(\alpha_{p} , \beta_{p} , \phi_{p}\) given by

$$\eta_{10} = \alpha_{0} \left( {1 + \alpha_{p} } \right)e^{{ - i\tau \Delta \omega_{1} }} , \eta_{01} = \beta_{0} \left( {1 + \beta_{p} } \right)e^{{ - i\tau \Delta \omega_{2} }} , \overline{\phi } = \overline{\phi }_{0} \left( {1 + \phi_{p} } \right).$$
(15)

Inserting (15) in three Eqs. (9), (10), (11), linearizing and taking Fourier transform defined by

$$\overline{g}\left( {\lambda ,\sigma } \right) = \frac{1}{2\pi }\mathop {\smallint \smallint }\limits_{ - \infty }^{ + \infty } g\left( {\xi ,\eta } \right)e^{{ - i\left( {\lambda \xi + \sigma \eta } \right)}} {\text{d}}\xi {\text{d}}\eta ~,$$
(16)

we obtain the nonlinear dispersion relation given by

$$\begin{aligned} & \left[ {\left( {2\overline{\Omega } - \delta_{1} k_{2} \sigma } \right)^{2} - A_{ + } \left\{ {A_{ + } + 2\left( {\mu_{1} + CB_{ + }^{2} } \right)\alpha_{0}^{2} } \right\}} \right]\left[ {\left( {2\overline{\Omega } + \delta_{1} k_{2} \sigma } \right)^{2} - A_{ - } \left\{ {A_{ - } + 2\left( {\mu_{1} + CB_{ - }^{2} } \right)\beta_{0}^{2} } \right\}} \right] \\ & = 4A_{ + } A_{ - } \left( {\mu_{2} + CB_{ + } B_{ - } } \right)^{2} \alpha_{0}^{2} \beta_{0}^{2} , \\ \end{aligned}$$
(17)

where \(\overline{\Omega }\) represents the perturbed frequency and \(A_{ \pm } , B_{ \pm } , C\) are given by

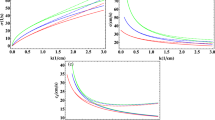
$$\begin{aligned} & A_{ \pm } = \delta_{2} \left( {k_{1} \lambda \pm k_{2} \sigma } \right)^{2} + \delta_{3} \left( {k_{2} \lambda \mp k_{1} \sigma } \right)^{2} , \\ & B_{ \pm } = \left\{ {2 + \left( {1 - \mu^{2} } \right)\overline{{c_{g} }} } \right\}k_{1} \lambda \pm 2k_{2} \sigma ,C = \frac{1}{{\left( {\gamma_{1} \lambda^{2} + \gamma_{2} \sigma^{2} } \right)}}. \\ \end{aligned}$$
(18)

In Figs. 1 and 2, we have plotted a contour plot of the instability growth rate \(G_{r} = \Omega_{i}\). From the figures, we have observed that the instability growth rate increases due to the effect of capillarity. Further, in Fig. 1, we have seen that the instability growth rate is slightly elevated as compared to Fig. 2. Also, in both subfigures of Fig. 3 and the left subfigure of Fig. 4, it is seen that the instability growth rate increases due to the capillarity effect. Furthermore, from these subfigures, we infer that \(G_{r}\) increases with the increment of water depth \(h\) as well as the wave steepness \(\beta_{0}\) of the second wave, whereas \(G_{r}\) decreases as the angle \(\theta\) between the two waves increases. Finally, from the right subfigure of Fig. 4, in the case of infinite depth fluid, the reverse effect of capillarity is noticed, and the instability growth rate is reduced as compared to finite depth fluid.

Fig. 1
figure 1

Contour plot of instability growth rate \(G_{r} = \Omega_{i}\) in \(\left( {\lambda ,\sigma } \right)\) plane for \(\alpha_{0} = \beta_{0} = 0.1,h = 2,s = 0\) (left), \(s = 0.035\) (right)

Full size image
Fig. 2
figure 2

Contour plot of instability growth rate \(G_{r} = {\Omega }_{i}\) in \(\left( {\lambda ,\sigma } \right)\) plane for \(\alpha_{0} = 0.12,\beta_{0} = 0.07,h = 2,s = 0\) (left), \(s = 0.035\) (right)

Full size image
Fig. 3
figure 3

Instability growth rate \(G_{r} = \Omega_{i}\) for \(\alpha_{0} = \beta_{0} = 0.1,\theta = 75^\circ ,h = 3,6,s = 0,0.035\) (left); for \(\alpha_{0} = \beta_{0} = 0.1,h = 2.5,\theta = 10^\circ ,23^\circ ,s = 0,0.035\) (right)

Full size image
Fig. 4
figure 4

Instability growth rate \(G_{r} = \Omega_{i}\) for \(\alpha_{0} = 0.1,h = 2.5,\theta = 15^\circ\), \(\beta_{0} = 0,0.05,0.1,s = 0,0.035\) (left); for \(\alpha_{0} = \beta_{0} = 0.1,h \to \infty ,\theta = 75^\circ ,s = 0,0.035\) (right)

Full size image

5 Conclusion

We have established two-coupled third-order NLSE for obliquely propagating capillary gravity waves over finite depth, which are valid for any water depth values apart from shallow water depth. Based on these NLSE, stability analysis is then made for two Stokes wave systems. Figures that have been drawn demonstrate the instability growth rate for different water depth values and various angles of the interaction of two-wave trains. It is observed from the graphs that the growth rate of instability over a finite depth of water for obliquely interacting wave trains is much elevated than the case of modulation in deep water, and it increases as the water depth decreases. Further, the instability growth rate for obliquely propagating wave trains is again much higher than the case of modulation for single wave trains. We have also investigated the effect of capillarity on modulational instability.