Keywords

1 Introduction

In today’s highly competitive global market, transportation models can maximize profit and minimize costs. Transportation problems (TPs) involve the transportation of items from different origins to different destinations. The classical TP developed by Hitchcock [9] and the transportation costs (TCs), demand, and supply are fixed numbers.

In real-life situations, fixed numbers do not come about naturally. In uncertain environments, Zimmermann [19] elevates a TP to a new model, which he labels as a fuzzy transportation problem (FTP). One FTP was formulated on the basis of the integer–value problem of Chanas and Kuchta [3]. Bellman and Zadeh [18] also aimed to solve FTPs with their technique. Pandian and Natarajan [12] aimed to find the optimal solution to the TCs, demand, and supply, which first requires using trapezoidal fuzzy numbers (TFNs). The optimal solution to any problem depends on the design function.

In the literature, a few initial basic feasible solutions are available, including the northwest corner method (NWCM) [10], the least cost method (LCM) [10], Vogel’s approximation method (VAM) [13], Goyal’s version of VAM (GVAM) [8], and the initial basic feasible solution (IBFS) proposed to the TP [1, 4, 5]. Also, many researchers have modified VAM to obtain an IBFS to the TP. In general, TPs are solved in fixed environments, but fixed environments do not appear in nature.

In the literature [6, 7, 11, 14,15,16,17], TFNs have been converted into fixed values, and researchers have used the robust ranking technique to solve FTPs. In this chapter, a TFN is converted into a fixed number by using the median method of ranking functions to solve FTPs. In this chapter, we present an SFZM and achieve the optimal solution. Our latest results are then compared with those from [10, 12,13,14].

2 Groundwork

In this section, we present a basic definition of TFN and a basic definition of the median ranking method.

2.1 Definition [12]

A fuzzy set \( \overset{\sim }{\rho } \) serves as a fuzzy number whose membership function has the following characteristics:

  • \( {\nu}_{\overset{\sim }{\rho }}\left(\zeta \right):= \rho \to \left[0,1\right] \) is continuous.

  • \( {\nu}_{\overset{\sim }{\rho }}\left(\zeta \right)=0\ \textrm{for}\ \textrm{all}\ \zeta \in \left(-\infty, {\zeta}_1\right]\cup \left[{\zeta}_4,\infty \right). \)

  • \( {\nu}_{\overset{\sim }{\rho }}\left(\zeta \right)\ is\stackrel{\longrightarrow}{\leftarrow} \textrm{strictly}\ \textrm{increasing}\ \textrm{for}\ \left[{\zeta}_1,{\zeta}_2\right]\ \textrm{and}\ \textrm{strictly}\ \textrm{decreasing}\ \textrm{for}\ \left[{\zeta}_3,{\zeta}_4\right]. \)

  • \( {\nu}_{\overset{\sim }{\rho }}\left(\zeta \right)=01\ \textrm{for}\ \textrm{all}\ \zeta \in \left[{\zeta}_2,{\zeta}_3\right],\textrm{where}\ {\zeta}_1<{\zeta}_2<{\zeta}_3<{\zeta}_4. \)

2.2 Definition [12]

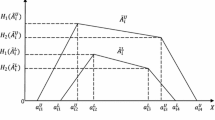
A fuzzy number, \( \overset{\sim }{\rho }=\left({\zeta}_1,{\zeta}_2,{\zeta}_3,{\zeta}_4\right) \), is a TFN if its membership function is given by the following:

$$ {\nu}_{\overset{\sim }{\rho }}\left(\zeta \right)=\left\{\begin{array}{c}\frac{\left(\zeta -{\zeta}_1\right)}{\left({\zeta}_2-{\zeta}_1\right)},{\zeta}_1\le \zeta \le {\zeta}_2,\\ {}1,{\zeta}_2\le \zeta \le {\zeta}_3,\\ {}\frac{\left(\zeta -{\zeta}_4\right)}{\left({\zeta}_3-{\zeta}_4\right)},{\zeta}_3\le \zeta \le {\zeta}_4,\\ {}0,\textrm{otherwise}.\end{array}\right. $$

2.3 Ranking Function [2]

Let \( \overset{\sim }{\rho }=\left({\zeta}_1,{\zeta}_2,{\zeta}_3,{\zeta}_4\right) \) be the TFN, in which case the median ranking method yields \( \mathfrak{R}\left(\overset{\sim }{\rho}\right)=\left(\frac{\zeta_2+{\zeta}_3}{2}\right) \)

3 Proposed Algorithm

In this section, the steps for the SFZM are presented, as follows:

Step 1.

  • An unbalanced FTP refers to a balanced FTP that has zero fuzzy costs (ZFCs), adding minimum fuzzy cost.

Step 2.

  • The total supply ≠ the total demand, so ZFCs are added.

Step 3.

  • 3(a) Select the lowest fuzzy cost (FC) value in each row, and then remove that from the FC values in that row.

  • 3(b) Select the lowest FC value in each column, and then remove that from the FC values in that column. At minimum, one ZFC should now be available in each row and each column.

  • Step 4.

  • 4(a) Confirm that the total fuzzy supply is lower than or equal to the total fuzzy demand.

  • 4(b) Confirm that the total fuzzy demand is now lower than or equal to the total fuzzy supply.

  • 4(c) If Step 4(a) and Step 4(b) have been completed, then jump ahead to Step 7; otherwise, proceed to Step 5.

Step 5.

  • The lowest-level lines are drawn parallel and perpendicular to the ZFCs in Step 3.

Step 6.

  • 6(a) Starting from any cell not enclosed by lines, select the lowest FC.

  • 6(b) Remove each FC in a cell not enclosed by lines.

  • 6(c) Add to each (FC) in a cell enclosed by two lines.

  • 6(d) If an FC in a cell enclosed by lines remains unchanged, then return to Step 4.

Step 7.

  • 7(a) Select the lowest fuzzy TC value from Step 4.

  • 7(b) Select a row single fuzzy-zero cell (RSFZC) and a column single fuzzy-zero cell (CSFZC) for allocation.

  • 7(c) Allocate the maximum possible, and cross off in the usual manner.

  • 7(d) If an RSFZC or a CSFZC does not appear in both rows and columns, then repeat the process from Step 7(a) to Step 7(c) until this requirement has been satisfied.

4 Numerical Examples

4.1 Fuzzy Data for Example 1 [12, 14] (Table 1)

The chosen fuzzy data for Example 1 are balanced. We used the median ranking method for the defuzzification process (Tables 2 and 3).

Table 1 Supply Vs Demand
Full size table
Table 2 Defuzzied data for Example 1
Full size table
Table 3 Northwest corner method (NWCM) [10]
Full size table

The minimum TC value according to the NWCM fixed cost is ₹138.5 (Table 4).

Table 4 Least cost method (LCM) [10]
Full size table

The minimum TC value according to the LCM fixed cost is ₹134.5 (Table 5).

Table 5 Vogel’s approximation method (VAM) [13]
Full size table

The minimum TC value according to VAM’s fixed cost is ₹123.5 (Table 6).

Table 6 Modified distribution method (MODI) [10]
Full size table

The minimum TC value according to the modified distribution method’s fixed cost is ₹121 (Table 7).

Table 7 SFZM
Full size table

The minimum TC value according to the SFZM’s fixed cost is ₹121.

4.2 SFZM with [10, 12,13,14]

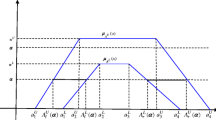
According to a comparison of the SFZM with the methods from [10, 12,13,14], as shown in Table 8, SFZM clearly provides lowest cost and thus the optimal result (Table 9; Figs. 1 and 2).

Table 8 Comparison of SFZM with other methods, including those from [10, 12,13,14]
Full size table
Table 9 The deviation percentage of various methods
Full size table
Fig. 1
A histogram of comparison of the S F Z M. The values and deviation percentage of N W C R is 138.5, 12.65, L C M is 134.5, 10%, 12 is 132.17, 8.5%, V A M is 123.5, 2%, 14 is 122.5, 1.2%, M O D I is 121, and S F Z M is 121, at 0%, respectively.

Comparison to the other existing methods (bar chart)

Full size image
Fig. 2
A line graph of deviation percentage versus existing methods. The line starts with N W C R at 12.6, L C M at 10, V A M at 2, 12 at 8.5, 14 at 1.2, M O D I at 0, and ends at S F Z M at 0.

The deviation percentage of other existing methods (up and down graph)

Full size image

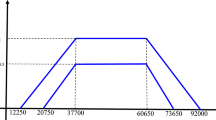
4.3 Fuzzy Data for Example 2 [14] (Tables 10, 11 and 12; Figs. 3 and 4)

Table 10 Fuzzy Supply Vs Fuzzy Demand
Full size table
Table 11 The deviation Value (₹) of various methods
Full size table
Table 12 The deviation percentage of various methods
Full size table
Fig. 3
A histogram of fuzzy data of example 2. The values and deviation percentage of N W C R is 685, 18.2%, L C M is 610, 8.2%, 14 is 577.5, 3.1%, V A M is 560, M O D I is 560, and S F Z M is 560 at 0%, respectively.

The deviation percentage of other existing methods (bar chart)

Full size image
Fig. 4
A line graph of deviation percentage versus existing methods. The line starts with N W C R at 18.2, L C M at 8.2, V A M at 0, 14 at 3.1, M O D I at 0, and S F Z M at 0, respectively.

The deviation percentage of other existing methods (up and down graph)

Full size image

4.4 Merits of Using the SFZM

In this chapter, the SFZM converted TFNs into fixed numbers, and we compared our results with those from [10, 12,13,14], which shows that the SFZM offers better solutions than those offered in [10, 12,13,14]. The SFZM also has the following merits:

  1. 1.

    The SFZM is easy to understand.

  2. 2.

    The SFZM achieves the optimal solution.

  3. 3.

    The SFZM is not needed to find the initial basic feasible solution.

  4. 4.

    SFZM solutions can be compared with [10, 12,13,14] by using fixed numbers.

5 Conclusion

In this chapter, the SFZM used the mean ranking method to convert the TFNs of transportation problems into fixed numbers.

  • For the total cost of Example 1, the results of the SFZM solution, in Table 8, show that value to be ₹121, which is better than the cost of [12] and that of [14], which were ₹132.17 and ₹122.5, respectively.

  • For the total cost of Example 2, the results of the SFZM solution, in Table 11, show that value to be ₹560, which is better than the cost of [14], which was ₹577.5.