Modified EC2 Model for the Shear Strength of RC Beams with Stirrups

Abstract

A modification of the variable strut inclination method of the Eurocode 2 (EC2) for the shear strength calculation of reinforced concrete (RC) beams with stirrups is presented. This model incorporates two (rather than one) variable-inclination compression struts. The upper compression strut may have lower inclination than the lower compression strut, which is indicated by the trend of the principal compressive stress direction. Following the theoretical framework of the EC2 approach, the two inclination angles are determined through the lower-bound theorem of plasticity, by solving an optimization problem. The proposed truss model leads to compact closed-form expressions that can be expediently used for practical design purposes. Based on comparison with experimental results, the proposed model proves to be more accurate than the Eurocode approach to predict the actual shear strength of RC beams with stirrups, especially in the range of low amounts of transverse reinforcement where the EC2 model turns out to be very conservative.

1 Introduction

The most famous and oldest approach for the shear strength calculation of reinforced concrete (RC) elements is the strut and tie model associated with the names of Ritter and Mörsch (Ritter 1899; Mörsch 1908). This model is formed by parallel chords and web members, the latter representing concrete compression struts and steel tensile ties. Despite its simplicity and conceptual meaningfulness, the Ritter- Mörsch truss model was found to underestimate the shear capacity of RC beams (Leonhardt 1973). Indeed, some contributions in the shear transfer mechanism of RC beams with stirrups, such as aggregate interlock and residual tensile stresses across cracks (ACI 445R-99 1988), as well as uncracked concrete contribution in the compression chord (Marí et al. 2015), are ignored in the Ritter-Mörsch model. More importantly, the inclination angle of the compression struts is assumed equal to 45° in the Ritter-Mörsch truss model, whereas experimental evidence reveals that the strut inclination angle at failure θ is generally lower than 45° (Walraven et al. 2013) and is actually variable as the shear force increases. Such experimental findings have motivated the development of so-called variable strut inclination methods, wherein θ is assumed variable and is determined from case to case according to additional criteria. Many options were studied to evaluate an appropriate value of θ, e.g., through compatibility conditions as per the modified compression field theory (MCFT) (Vecchio and Collins, 1986), or exploiting the theory of plasticity (Nielsen & Hoang 1999). According to the lower-bound theorem of plasticity, the angle θ can be established as the angle that, within the class of statically and plastically admissible solutions, maximizes the shear strength. Such plasticity-based approaches are very attractive from a design point of view because they only resort to simple equilibrium conditions without any explicit consideration to compatibility. A plasticity-based variable strut inclination model was adopted in the Model Code 90 (fib 1993) and in the Eurocode 2 (EC2 2005), as well as in the Italian Building Code (NTC 2018), and in the German Building Code (DIN 1045–1 2009).

A drawback of the aforementioned variable strut inclination model of the EC2 (hereinafter called simply “EC2 truss model”) is that one single strut inclination of the compression strut is adopted to describe the shear stress distribution along the beam height. Nevertheless, the shear stresses generally increase in the upper part of the beam, near the uncracked compression chord in the neighbourhood of the crack tip, in comparison to the lower part. According to Mohr’s circle principles and the isostatic lines of compression, this non-uniform shear stress distribution is reflected in a significant rotation of the principal compressive stress direction in the upper portion of the beam compared to the lower portion, which physically motivates the introduction of a second strut with a reduced inclination angle. Based on these mechanical considerations, this contribution presents an upgrade of the EC2 truss model with two (rather than one) variable-inclination compression struts (De Domenico and Ricciardi 2019). The upper compression strut may have lower inclination than the lower compression strut to describe the aforementioned trend of isostatic lines of compression. The two inclination angles are determined through simple equilibrium conditions and the lower-bound theorem of plasticity through closed-form expressions that can be expediently used for practical design purposes. Based on comparison with experimental results from the ACI-DafStb databases (Reineck et al. 2014), the proposed modified EC2 truss model turns out to be more accurate than the EC2 single-strut approach, especially in the range of low amounts of transverse reinforcement where the EC2 model turns out to be very conservative.

2 Mechanical Motivations

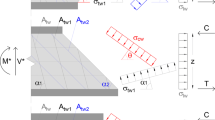
Let us consider a beam subjected to three-point bending test. Let us assume that such beam is designed to fail in shear. As shown in Fig. 1, diagonal cracks develop from the supports to the loading point. Moreover, the concurrent bending effects generate a variability of the crack widths, which decrease from the lower portion going upwards near the compression zone (in the neighbourhood of the crack tip). Hence, as the shear force increases a shear stress redistribution occurs. It has been experimentally observed that at incipient failure the shear stresses in the upper portion of the beam (near the uncracked compression chord) are much higher than in the lower portion (Marí et al. 2016). A preliminary stress analysis under the hypothesis of plane stress conditions is useful to identify the principal compressive stress directions, as shown in Fig. 1.

Fig. 1.

Crack pattern and qualitative shear stress distribution across cracks for a RC beam failing in shear (modified from Regan 1969), along with identification of principal compressive stress direction through Mohr’s circles.

In particular, for a generic element P located in the lower portion of the beam (associated with larger crack widths), the shear stress τ₁ is relatively low. The principal compressive stress direction of point P is denoted $\theta_{1}$ and is generally slightly lower than 45°. Indeed, experimental findings reveal that some cracks having inclinations < 45° pass through the first cracks at around 45° as the shear force increases (Walraven et al. 2013). On the other hand, for an element Q located in the upper portion of the beam (associated with much lower crack width, near the compression zone) the shear stress τ₂ is expected to be much higher than τ₁ for a comparable value of normal stress σ. Based on Mohr’s circles, the higher shear stress of point Q combined with a comparable normal stress gives rise to a reduced inclination angle $\theta_{2} < \theta_{1}$. This is fully consistent with the typical trend of isostatic lines of compression, in which the principal compressive stress directions are more inclined (tending to be almost horizontal) in the upper-mid portion of the beam. These considerations, valid for two generic points P and Q, can be extended to other points, and the trend of principal compressive stress directions is expected to vary gradually along the beam height.

In the EC2 truss model, one single value of the compression struts is allowed (EC2 2005), which is determined through equilibrium conditions and in the framework of the lower-bound theorem of plasticity (Nielsen and Hoang 1999). Consequently, the above-described variability of the principal compressive stress direction due to the shear stress distribution along the beam height cannot be incorporated. As a straightforward extension of the single strut model of the EC2, in this contribution two (rather than one) representative inclination angles of the compressive struts, one for the lower-mid part $\theta_{1}$ and the other for the upper-mid part $\theta_{2} < \theta_{1}$, are introduced. The additional strut inclination $\theta_{2}$ in the upper-mid part of the beam aims to capture, in a simplified manner, the mechanism of shear stress increase in the neighborhood of the crack tip, close to the uncracked compression chord, in comparison to the lower portion of the beam wherein larger crack widths are observed. In line with the variable strut inclination method of the EC2, the determination of the two strut inclination angles $\theta_{1}$ and $\theta_{2}$ at beam failure is carried out by means of the theory of plasticity.

It is worth noting that such variability of the crack width is more pronounced for lightly shear reinforced beams, in which web crushing is preceded by yielding of stirrups and the phenomenon of strut rotation is more evident (He et al. 2015). Instead, as the shear reinforcement increases, the crack openings are controlled by stirrups, so that minimal strut rotations occur because the shear stresses tend to be more uniformly distributed along the beam height. In the latter case, the assumption of $\theta_{1} = \theta_{2}$ (as in EC2 model) is quite reasonable and the additional strut inclination angle introduced by the proposed formulation is not expected to lead to significant variations of the shear strength. This consideration will be verified in the numerical examples shown in the remainder of this paper.

3 Truss Model with Two Strut Inclination Angles

The shear resisting mechanism of the beam can be idealized with a truss model comprising two parallel chords (top concrete stress block having resultant C and bottom longitudinal reinforcement having resultant T) and web members, namely compression struts (representing the stress fields in concrete) and tensile ties (representing the effect of stirrups). The spacing of stirrups is assumed sufficiently small, so that their effect can be modelled with uniform stress fields according to a smeared truss model (Marti 1985), while uniform compressive stress fields are assumed for concrete. Let us denote with $\alpha$ the inclination angle of the transverse reinforcement with respect to the longitudinal axis of the beam, and with θ the compression strut inclination. In the EC2 (EC2 2005) values of $1 \le \cot \theta \le 2.5$ are allowed, which correspond to $21.8^\circ \le \theta \le 45^\circ$. These limitations may change depending on the country (Grandić et al. 2015).

Based on the plasticity theory, the shear strength of a RC beam is determined through simple equilibrium equations considering two different beam segments (according to Ritter’s method), as shown in Fig. 2. First, the vertical equilibrium on a section parallel to the compression strut is written (Fig. 2-top). The regions to which two strut inclinations extend are identified by a parameter $\beta$, with $0 < \beta < 1$: in particular, in the upper portion of depth $\beta z$ ($z$ representing the inner lever arm), the strut inclination angle is $\theta_{2}$, while in the lower portion of complementary depth $(1 - \beta )z$, the strut inclination is $\theta_{1}$. In general, the value of $z$ can be assumed as $0.9d$, where $d$ indicates the effective depth of the beam. Assuming a constant spacing $s$ and denoting with $\sigma_{sw1}$ and $\sigma_{sw2}$ the uniform stress fields of the steel transverse reinforcement in the two portions, and with $A_{sw}$ the area of the corresponding cross section, the vertical equilibrium of the forces acting on the considered beam segment leads to

$$\begin{gathered} V = S_{sv} = S_{sv1} + S_{sv2} = S_{s1} \sin \alpha + S_{s2} \sin \alpha \hfill \\ = [\left( {\sigma_{sw1} /f_{ywd} } \right)(1 - \beta )(\cot \theta_{1} + \cot \alpha ) + \left( {\sigma_{sw2} /f_{ywd} } \right)\beta (\cot \theta_{2} + \cot \alpha )]b_{w} z{\kern 1pt} \nu_{1} f_{cd} \omega_{w} \left( {\sin \alpha } \right)^{2} \hfill \\ \end{gathered}$$

(1)

where the so-called “mechanical ratio of transverse reinforcement” is defined as

$$\omega_{w} = \frac{{A_{sw} }}{{b_{w} s\sin \alpha }}\frac{{f_{ywd} }}{{\nu_{1} f_{cd} }} = \rho_{w} \frac{{f_{ywd} }}{{\nu_{1} f_{cd} }}.$$

(2)

Fig. 2.

Ritter’s method parallel to compression struts (top) and to transverse reinforcement (bottom) to identify internal forces.

In Eqs. (1) and (2), $b_{w}$ denotes the minimum web width, $\rho_{w} = A_{sw} /(sb_{w} \sin \alpha )$ the transverse reinforcement ratio, $f_{ywd}$ is the design yield strength of the transverse reinforcement, $f_{cd}$ is the design value of concrete compressive strength and $\nu_{1}$ a strength reduction factor (or efficiency factor) that synthetically quantifies the reduction of the concrete strength due to cracking in shear. Typical values of $\nu_{1}$ are in a range 0.5–0.6. Assuming the limit condition $\sigma_{sw1} = \sigma_{sw2} = f_{ywd}$ the following expression is obtained

$$V_{Rd,s} = b_{w} z{\kern 1pt} \nu_{1} f_{cd} \omega_{w} \times \left[ {\cot \alpha + cot\theta_{1} + \beta \left( {\cot \theta_{2} - \cot \theta_{1} } \right)} \right]\left( {\sin \alpha } \right)^{2}$$

(3)

which represents the shear strength due to yielding of transverse reinforcement.

As a second step, a section parallel to the transverse reinforcement is considered (Fig. 2-bottom). Again, assuming uniform stress fields $\sigma_{cw1}$ and $\sigma_{cw2}$ of concrete in the lower and upper portion of the beam, the vertical equilibrium of acting forces yields

$$\begin{gathered} V = S_{cv} = S_{cv1} + S_{cv2} = S_{c1} \sin \theta_{1} + S_{c2} \sin \theta_{2} = \hfill \\ \, = b_{w} z{\kern 1pt} \nu_{1} f_{cd} [\left( {\sigma_{cw1} /\nu_{1} f_{cd} } \right)(1 - \beta )\frac{{\left( {\cot \theta_{1} + \cot \alpha } \right)}}{{1 + \left( {\cot \theta_{1} } \right)^{2} }} + \left( {\sigma_{cw2} /\nu_{1} f_{cd} } \right)\beta \frac{{\left( {\cot \theta_{2} + \cot \alpha } \right)}}{{1 + \left( {\cot \theta_{2} } \right)^{2} }}] \hfill \\ \end{gathered}$$

(4)

In the limit condition $\sigma_{cw1} = \sigma_{cw2} = \nu_{1} f_{cd}$

$$V_{Rd,c} = b_{w} z{\kern 1pt} \nu_{1} f_{cd} \times [(1 - \beta )\frac{{\left( {\cot \theta_{1} + \cot \alpha } \right)}}{{1 + \left( {\cot \theta_{1} } \right)^{2} }} + \beta \frac{{\left( {\cot \theta_{2} + \cot \alpha } \right)}}{{1 + \left( {\cot \theta_{2} } \right)^{2} }}]$$

(5)

which represents the shear strength due to crushing of concrete compression struts.

In the following discussions, Eqns. (3) and (5) will be used in dimensionless form by dividing them with the normalization parameter $r = b_{w} z{\kern 1pt} \nu_{1} f_{cd}$. This is convenient for practical design purposes. The obtained dimensionless expressions can be further simplified under the common assumption of vertical shear reinforcement ($\alpha = 90^\circ$, $\cot \alpha = 0$), and $\beta = 1/2$ (meaning that the two strut inclinations are equally extended for a half of the inner lever arm), which leads to

$$\begin{gathered} v_{Rd,s} = \left. {\frac{{V_{Rd,s} }}{r}} \right|_{\alpha = 90^\circ } = \frac{{\omega_{w} }}{2}\left[ {cot\theta_{1} + \cot \theta_{2} } \right] \hfill \\ v_{Rd,c} = \left. {\frac{{V_{Rd,c} }}{r}} \right|_{\alpha = 90^\circ } = \frac{1}{2}\left[ {\frac{{\cot \theta_{1} }}{{1 + \left( {\cot \theta_{1} } \right)^{2} }} + \frac{{\cot \theta_{2} }}{{1 + \left( {\cot \theta_{2} } \right)^{2} }}} \right] \hfill \\ \end{gathered}$$

(6)

The assumption $\beta = 0.5$ not only simplifies the analytical formulation by facilitating the derivation of analytical solutions of the general optimization problem, but it also represents the most logical choice to describe the progressive (and continuous) variation of the principal compressive stress directions along the height of the beam, by placing the transition of the two representative strut inclination angles at the middle of the inner lever arm. The two angles $\theta_{1}$ and $\theta_{2}$ should therefore be interpreted as the average angles in the two lower and upper mid-portions of the beam heights, respectively.

By inspection of Eq. (6), we note that $v_{Rd,s}$ is a linear function of the variables $\cot \theta_{1}$ and $\cot \theta_{2}$, whereas $v_{Rd,c}$ is a nonlinear function of the two cotangent variables. The case $\beta = 0$ (or, equivalently, $\theta_{1} = \theta_{2}$) corresponds to the EC2 single strut model. According to the lower-bound theorem of plasticity theory (Nielsen and Hoang 1999; De Domenico and Ricciardi 2020; De Domenico 2021), the actual shear strength is the smaller value of the two contributions

$$v_{Rd} = v_{Rd} \left( {\omega_{w} ,\theta_{1} ,\theta_{2} } \right) = \min \left( {v_{Rd,s} ,v_{Rd,c} } \right)$$

(7)

and a rational design solution is such that a simultaneous collapse mechanism (concrete crushing and steel yielding) takes place, which is given by

$$v_{Rd,s} \left( {\tilde{\theta }_{1} ,\tilde{\theta }_{2} } \right) = v_{Rd,c} \left( {\tilde{\theta }_{1} ,\tilde{\theta }_{2} } \right)$$

(8)

Similar to the EC2 truss model, when searching the two strut inclination angles some limitations should be taken into account. With regard to the lower strut inclination angle, the same limitation as in the EC2 model can be adopted, namely $1 \le \cot \theta_{1} \le 2.5$ or $21.8^\circ \le \theta_{1} \le 45^\circ$. Instead, the upper strut inclination angle can have a wider range of variability, considering that values $\theta_{2} < \theta_{1}$ can occur, as explained in the previous section (cf. Again Fig. 1). In this paper, a reasonable variation interval $1 \le \cot \theta_{2} \le 5.0$ is assumed. According to the lower-bound theorem of plasticity, the actual shear strength of the RC beam is sought in the class of statically and plastically admissible solutions (i.e., strut inclination angles satisfying equilibrium conditions and leads to stresses nowhere exceeding the yield conditions) according to the following optimization problem

$$\mathop {\max }\limits_{{\theta_{1} ,\theta_{2} }} v_{Rd} (\overline{\omega }_{w} ,\theta_{1} ,\theta_{2} )\quad \quad s.t.\left\{ \begin{gathered} 1 \le \cot \theta_{1} \le 2.5 \hfill \\ 1 \le \cot \theta_{2} \le 5.0 \hfill \\ \end{gathered} \right.$$

(9)

where an additional physical condition is $\theta_{2} < \theta_{1}$

Fig. 3.

Couples of strut inclination angles $\theta_{1}$ and $\theta_{2}$ that allow the simultaneous collapse mode of yielding of stirrups and crushing of compressive struts (rational design solution).

In Fig. 3 the couples of strut inclination angles $\theta_{1}$ and $\theta_{2}$ that allow the simultaneous collapse mode of stirrup yielding and concrete crushing (rational design solution) are depicted for different values of shear reinforcement ratio $\omega_{w}$ in the range 0.10–0.25. The condition $\cot \theta_{2} = \cot \theta_{1}$ is also shown in the plot as a blue dotted line to identify the EC2 design solutions (single strut approach). The physical condition $\theta_{2} < \theta_{1}$ implies that the sector of the plot lying above the bisector line should be excluded. The EC2 rational design solution is expressed by the following condition in terms of strut inclination angle

$$\cot \tilde{\theta }^{{{\text{EC2}}}} = \sqrt {\frac{{1 - \omega_{w} }}{{\omega_{w} }}}$$

(10)

which is represented by the blue circles shown in Fig. 3.

However, there exists a much broader range of admissible rational design solutions allowed by the proposed truss model with two strut inclination angles lying in the admissible domain (i.e., in the shaded rectangular box). This means that the introduction of the second strut inclination angle significantly widens the range of statically admissible solutions (in terms of couples $\theta_{1}$ and $\theta_{2}$) for the assessment of the shear capacity of the RC beam. According to the static theorem of limit analysis, the lower bound to the actual shear capacity is the highest value of shear strength that is associated with the class of statically admissible couples $\theta_{1}$ and $\theta_{2}$. Moreover, while for the EC2 the rational design solutions are represented by a single point for a given $\omega_{w}$ (intersection of two lines $v_{Rd,s} (\theta )$ and $v_{Rd,c} (\theta )$), in the proposed truss model the rational design solutions are represented by a line for a given $\omega_{w}$ (intersection of two surfaces $v_{Rd,s} (\theta_{1} ,\theta_{2} )$ and $v_{Rd,c} (\theta_{1} ,\theta_{2} )$) as shown in Fig. 4. In this figure, the surface $v_{Rd}$ defined in Eq. (9) for a given $\omega_{w} = 0.15$ is plotted in the range $1 \le \cot \theta_{i} \le 5$ (i = 1,2). The solution of the single strut inclination method of the EC2 is represented by the blue circle, lying on the bisector line $\cot \theta_{2} = \cot \theta_{1}$ on the ridge of the surface. This point is characterized by $\tilde{\theta }^{EC2} = 22.79^\circ$ and $v_{Rd}^{EC2} = 0.357$. However, other rational design solutions of the truss model with two strut inclinations are possible, which are represented by the thick black line identified by the condition $v_{Rd,s} (\theta_{1} ,\theta_{2} ) = v_{Rd,c} (\theta_{1} ,\theta_{2} )$ The optimal solution in the framework of the theory of plasticity is the red square point characterized by the highest value of the shear strength along the thick black line. This point is identified by coordinates $\theta_{1}^{opt} = 41.29^\circ$, $\theta_{2}^{opt} = 14.72^\circ$ and shear strength $v_{Rd}^{opt} = 0.371$. Interestingly, the value of the EC2 angle $\tilde{\theta }^{EC2} = 22.79^\circ$ is intermediate between the two strut inclination angles of the proposed truss model for the specific case $\omega_{w} = 0.15$ considered in this example. Although not explicitly reported here for the sake of brevity, it can be demonstrated that the two strut inclination angles as well as the shear strength resulting from the optimization problem (9) can be expressed in closed-form through practical analytical expressions (De Domenico and Ricciardi 2019). Generalizing this procedure to other shear reinforcement ratios $\omega_{w}$, it is possible to construct a curve representing the shear strength versus the shear reinforcement ratio and to compare this curve to the EC2 curve. This comparison is shown in Fig. 5.

The excessive conservative nature of the Ritter-Mörsch truss model is clearly seen in Fig. 5. The figure also shows that the plasticity theory would predict higher shear strength than those of the EC2 truss model in the range of low transverse reinforcement. This is due to the lower bound limitation of the $\theta$ angle in the EC2 approach ($\theta_{\min } = 22.8^\circ$). For all $\omega_{w}$ values < 0.137 (Eurocode 2 design region I) the $\theta$ angle is set as the minimum possible value $\theta = \theta_{\min } = 22.8^\circ$, corresponding to $\cot \theta = 2.5$. For higher shear reinforcement ratios, the curves of the EC2 model and of the plasticity theory coincide.

Different design regions can be identified in the proposed truss model, depending on the amount of transverse reinforcement. In particular, in the so-called design regions 1,2,3 (corresponding to $0 \le \omega_{w} \le 0.0716$, $0.0716 \le \omega_{w} \le 0.1136$ and $0.1136 \le \omega_{w} \le 0.25$, respectively), the shear strength predicted by the proposed truss model is higher than that of the EC2 model, while for $\omega_{w} \ge 0.25$ (design region 4) that two models coincide with each other as the two strut inclination angles determined by solving the optimization problem in (9) are such that $\theta_{1} = \theta_{2}$.

Fig. 4.

Class of rational design solutions and identification of optimal couple of strut inclination angles $\theta_{1}$ and $\theta_{2}$ corresponding to the maximum shear capacity for $\omega_{w} = 0.15$.

Fig. 5.

Shear strength vs shear reinforcement ratio of the improved truss model with two strut inclination angles compared to the EC2 single strut model, plasticity theory and Ritter-Mörsch truss model.

This result, obtained from an analytical point of view, is fully in line with the expectations and has evident physical justifications: excessive amounts of shear reinforcement lead to reduced crack widths and to a mitigation of the shear stress variability along the beam height. As a result, for high values of $\omega_{w}$, the second strut inclination in the upper portion of the beam plays no role and is aligned with the first strut inclination of the lower portion of the beam. Instead, for low amount of shear reinforcement, the crack widths are large and the consequent variability of the shear stresses generates a variability of the principal compressive stress directions.

4 Comparison with Experimental Data

The shear strength predictions of the improved truss model with two strut inclination angles are assessed against experimental results from the literature. Two well established collections of shear test results are considered in this paper, namely the ACI-DafStb databases reported by Reineck et al. (2014), Reineck and Dunkelberg (2017). These databases, characterized by transparent criteria for the selection of the experimental data, include a small database of 87 tests and a larger database (H. 617) of 170 tests. All the beams in the databases had vertical stirrups, were subjected to point loads, and failed in shear. The range of most important geometrical and mechanical parameters of the two databases is listed in Table 1.

Table 1. Range of geometrical and mechanical parameters in the ACI-DafStb databases.

The results are shown in dimensionless form by dividing the experimental shear strength with the normalization parameter $r = b_{w} z\nu_{1} f_{c}$ of each beam. This makes it possible to compare the predictive performance of the two truss models (EC2 and improved EC2) directly in the $\omega_{w} - v$ plane, as illustrated in Fig. 6 for the range of $\omega_{w} < 0.25$. Based on the comparison, it clearly emerges that the improved EC2 truss model (with two strut inclination angles) proposed in this contribution is better able to capture the trend of the experimental data than the EC2 truss model. This is especially true in the range of lightly shear reinforced beams (for $\omega_{w} < 0.1$) where the EC2 model seems to be excessively conservative. As a result, the introduction of the second strut inclination angle has allowed the construction of a wider class of statically admissible solutions and has allowed the achievement of shear strength values that are more in line with the experimental results.

Fig. 6.

Shear strength prediction of improved EC2 truss model with two strut inclination angles and EC2 truss model against experimental results from ACI-DafStb databases.

The better predictive performance of the proposed truss model is confirmed for both the small and the large ACI-DafStb databases. In particular, considering the entire ACI-DafStb small database, the mean $v_{\exp } /v_{pred}$ ratio is 1.39 for the EC2 model and 1.05 for the proposed truss model, and the coefficient of variation is 24.02% for the EC2 model and 18.49% for the proposed truss model. Instead, considering the entire ACI-DafStb large database, the mean $v_{\exp } /v_{pred}$ ratio is 1.56 for the EC2 model and 1.10 for the proposed truss model, and the coefficient of variation is 31.43% for the EC2 model and 23.06% for the proposed truss model. These results demonstrate that the proposed truss model with two strut inclination angles exhibits smaller bias and higher precision than the EC2 truss model in predicting the shear strength of a large number of beams.

5 Conclusions

The EC2 model for the shear strength calculation is based on the theory of plasticity, more precisely, on the static theorem of limit analysis. Indeed, the EC2 approach aims at maximizing the shear strength within the class of statically admissible solutions in terms of compressive strut inclination angle $\theta$. In the author’s opinion, the excessive conservativeness of the EC2 truss model in predicting the shear strength of beams with low amounts of transverse reinforcement is ascribed to the restricted class of statically admissible solutions for a single strut inclination angle. In reality, the principal compressive stress direction (governing the strut inclination angle) is variable along the beam height. This variability is strictly related to the shear stress increase in the upper portion of the beam, due to the concurrent bending effects that affect the crack widths. These variability effects are indeed more pronounced in the case of lightly shear reinforced beams, where the EC2 approach turns out to be over-conservative. In particular, the strut inclination angle should be lower in the upper portion of the beam compared to the lower portion of the beam. Based on these mechanical considerations, in this contribution a modified EC2 truss model with two strut inclination angles $\theta_{1}$ (in the bottom portion) and $\theta_{2} < \theta_{1}$ (in the upper portion) has been introduced. The value of the two inclination angles is determined in the framework of the static theorem of limit analysis, by solving an optimization problem. It can be demonstrated that the optimization problem leads to elegant and very compact closed-form expressions (De Domenico and Ricciardi 2019). In other words, the application of the proposed truss model for design purposes is of comparable simplicity to the EC2 model. The broader class of statically admissible solutions allowed by the modified EC2 truss model leads to higher values of the shear strength in the range of low shear reinforcement ratios. Based on a comparison with a large number of experimental results pertinent to the well-established ACI-DafStb databases, it has been demonstrated that the modified EC2 truss model proposed in this paper exhibits smaller bias and higher precision in comparison to the EC2 model, especially in the range of low amounts of transverse reinforcement.