Optimal Sensor Placement Considering Operational Sensor Failures for Structural Health Monitoring Applications

Abstract

A structural health monitoring (SHM) system acquires sensor measurements from which a structural state can be inferred. An updated understanding of the structural state is crucial in making appropriate maintenance decisions over the life cycle of the structure. However, the inferred structural state may be incorrect if the sensing system that initiates the SHM workflow is unreliable. The operational and environmental conditions that these sensors can face, in addition to normal manufacturing defects, result in varying functionality at different monitoring locations, at different times. Therefore, it is important to account for sensor reliability in the optimal sensor design process for the SHM system at the outset. In this chapter, we propose an optimal sensor design framework that accounts for the time-dependent reliability of the sensor network over the life cycle of the structure. The targeted objective function (Bayes risk) must consider the consequence of unreliable measurements over time, uncertainties in loading, sensor readings, and bias. This makes the Bayes risk a multidimensional integral with a non-linear integrand. The algorithm deploys the Bayesian optimization technique in tandem with univariate dimensional reduction and Gaussian-Hermite numerical approximation of the Bayes risk that catalyzes efficient numerical implementation of an otherwise computationally exhaustive process. We consider monitoring of a miter gate as the demonstration example and focus on the inference of an unknown and uncertain state-parameter(s) (i.e., damage from the loss of contact between the gate and wall, the “gap”) from the acquired sensor data.

14.1 Introduction

This chapter describes a sensor optimization framework with consideration of spatial and time-dependent sensor reliability. That is, the framework considers the possibility of sensors malfunctioning over time. The goal here is to design a reliable sensor network such that the measurements lead to a reliable inference of the damage state over the life cycle of the structure even in a situation where some sensors in the network have malfunctioned. This research is built on the Bayesian optimization-based sensor placement framework that we had developed in our previous works (see Yang et al. [1, 2]). A well-designed data acquisition system leads to an improvement in the Value of Information (see Chadha et al. [3]) and is crucial for reliable decision-making (see Chadha et al. [4]). The sensor optimization algorithm is applied to a complex real-world miter gate structure where different parts of the structure are exposed to different environmental conditions that dynamically change over time.

14.2 Problem Definition

We consider three scenarios of sensor reliability. In scenario 1, the sensor is perfectly functional (hence yields reliable readings) but has standard measurement noise. In scenario 2, the sensor is partially malfunctioning. Therefore, along with the standard measurement noise, the sensor readings also suffer from reliability bias. In scenario 3, the sensor has completely failed. In most cases, the third scenario can be easily recognized and rectified by an on-site repair/replacement. We focus on the second scenario of accounting for sensor reliability over the life cycle of the structure in an optimal sensor placement framework.

Consider a sensor design e ∈ Ω_E consisting of N_sg(e) number of sensors with the measurement ${x}_e(t)\in {\Omega}_{X_e(t)}$. Over its life cycle, a structure is subjected to uncertain loading, denoted by the random vector H(t) with a realization h(t) ∈ Ω_H(t). Let Θ(t) denote a random variable representing the state/damage parameter vector at any time t with a realization denoted by θ(t). Let the random vector ζ_e(t) represent the measurement noise (composed of standard observation noise and reliability bias), with a realization denoted by ${\varepsilon}_e(t)=\left({\varepsilon}_{e1}(t),{\varepsilon}_{e2}(t),\cdots, {\varepsilon}_{e{N}_{\textrm{sg}}(e)}(t)\right)\in {\Omega}_{\zeta_e(t)}$. We consider a general case where the structure is divided into various reliability zones depending on the parts of structures exposed to different environmental conditions [modeled by the loading term denoted by h(t)]. Let Ω_S = {s_unrel, s_rel} denote the set of functional states of the sensor, where s_unrel denotes that a sensor is malfunctional and unreliable (scenario 2) and s_rel represents a fully functional and reliable sensor (scenario 1). The probability mass functions ${P}_{S_{ei}(t)\mid H(t)}\left({s}_{\textrm{unrel}}|h(t)\right)$ and ${P}_{S_{ei}(t)\mid H(t)}\left({s}_{\textrm{rel}}|h(t)\right)=1-{P}_{S_{ei}(t)\mid H(t)}\left({s}_{\textrm{unrel}}|h(t)\right)$ denote the probability of the i-th sensor malfunction or fully functional at time t conditioned upon the loading zone [defined by the load vector h(t) and the sensor location of the i-th sensor in sensor array design e]. Let ${f}_{\zeta_{ei}(t)\mid H(t)}\left({\varepsilon}_{ei}(t)|h(t)\right)$ denote the distribution of observation noise in the i-th sensor conditioned upon the loading zone at which the sensor is installed (which is assumed to be defined in terms of various loading situations). The uncertainty in the measurements is contributed by two effects: (a) the standard observation noise of scenario 1 and (b) the reliability bias as a consequence of the sensor’s partial malfunction. That is,

$$ {\varepsilon}_{ei}(t)=\left\{\begin{array}{c}{\overline{\varepsilon}}_{ei}(t)\kern6.75em \textrm{for}\ \textrm{sensor}\ \textrm{functional}\ \textrm{state}\ {s}_{\textrm{rel}};\\ {}{\overline{\varepsilon}}_{ei}(t)+{n}_{ei}(t)\kern3.25em \textrm{for}\ \textrm{sensor}\ \textrm{functional}\ \textrm{state}\ {s}_{\textrm{unrel}}.\end{array}\right. $$

(14.1)

Here, n_ei(t) is a realization of the random variable η_ei (with the mean ${\mu}_{n_{ei}(t)}$ and standard deviation ${\sigma}_{n_{ei}(t)}$) that models the sensor reliability bias in the i-th sensor of the design e. ${\overline{\varepsilon}}_{ei}(t)$ is the standard observation noise for scenario 1 and it has a standard deviation of ${\sigma}_{{\overline{\varepsilon}}_{ei}(t)}$. The distribution of the measurement noise is then given by:

$$ {\displaystyle \begin{array}{c}{f}_{\zeta_{ei}(t)\mid H(t)}\left({\varepsilon}_{\textrm{e}i}(t)|h(t)\right)={P}_{S_{ei}(t)\mid H(t)}\left({s}_{\textrm{rel}}|h(t)\right)\frac{1}{\sigma_{{\overline{\varepsilon}}_{ei}(t)}}\ \phi \left(\frac{\varepsilon_{ei}(t)}{\sigma_{{\overline{\varepsilon}}_{ei}(t)}}\right)+\\ {}{P}_{S_{ei}(t)\mid H(t)}\left({s}_{\textrm{unrel}}|h(t)\right)\frac{1}{\sqrt{\sigma_{{\overline{\varepsilon}}_{ei}(t)}^2+{\sigma}_{n_{ei}(t)}^2}}\phi \left(\frac{\varepsilon_{ei}(t)-{\mu}_{n_{ei}(t)}}{\sqrt{\sigma_{{\overline{\varepsilon}}_{ei}(t)}^2+{\sigma}_{n_{ei}(t)}^2}}\right).\end{array}} $$

(14.2)

We obtain the observed sensor readings x_e(t) by adding the noise vector ε_e(t) to the exact/ground-truth value of the sensor measurement obtained using the FEM model g_e(θ_true(t), h(t); t). That is,

$$ {x}_e(t)={g}_e\left({\theta}_{\textrm{true}}(t),h(t);t\right)+{\varepsilon}_e(t). $$

(14.3)

Obtaining optimal sensor design using Bayesian optimization requires accessing the posterior distribution of the damage parameter θ(t) for a given measurement reading x_e(t) numerous times. The posterior distribution is obtained using Bayes theorem as ${f}_{\Theta (t)\mid {X}_{\textrm{e}}(t),H(t)}\left(\theta (t)|{x}_e,h\right)\propto {f}_{X_e(t)\mid \Theta \left(\textrm{t}\right)}\left({x}_e|\theta \right).{f}_{\Theta (t)}\left(\theta (t)\right)$. The likelihood is obtained using the measurement model for x_e defined in Eq. (14.1) and the observation noise structure defined in Eq. (14.2) as:

$$ \begin{aligned}{f}_{X_e(t)\mid \Theta \left(\textrm{t}\right)}\left({x}_e|\theta \right)= & \prod_{i=1}^{N_{\textrm{sg}}(e)}\left(\vphantom{\frac{\varepsilon_{ei}(t)-{\mu}_{n_{ei}(t)}}{\sqrt{\sigma_{{\overline{\varepsilon}}_{ei}(t)}^2+{\sigma}_{n_{ei}(t)}^2}}}{P}_{S_{ei}(t)\mid H(t)}\left({s}_{\textrm{rel}}|h(t)\right)\frac{1}{\sigma_{{\overline{\varepsilon}}_{ei}(t)}}\ \phi \left(\frac{\varepsilon_{ei}(t)}{\sigma_{{\overline{\varepsilon}}_{ei}(t)}}\right) \right. \\ & \left. +{P}_{S_{ei}(t)\mid H(t)}\left({s}_{\textrm{unrel}}|h(t)\right)\frac{1}{\sqrt{\sigma_{{\overline{\varepsilon}}_{ei}(t)}^2+{\sigma}_{{\textrm{n}}_{ei}(t)}^2}}\phi \left(\frac{\varepsilon_{ei}(t)-{\mu}_{n_{ei}(t)}}{\sqrt{\sigma_{{\overline{\varepsilon}}_{ei}(t)}^2+{\sigma}_{n_{ei}(t)}^2}}\right)\right). \end{aligned} $$

(14.4)

We use particle filtering technique for Bayesian inference of damage parameter θ(t) given the measurements x_e(t).

14.3 Objective Function Focused on Reliable Sensor Measurements

We define the risk of sensor bias at time t as the absolute deviation between the true state and the mean of the posterior:

$$ \mathcal{L}\left({\theta}_{\textrm{true}}(t),h(t),{\varepsilon}_e(t);t\right)=\left|{\mu}_{\Theta \left(\textrm{t}\right)\mid {\textrm{X}}_{\textrm{e}}(t),H(t)}-{\theta}_{\textrm{true}}(t)\right|. $$

(14.5)

The expected risk of sensor bias at time t is defined as follows:

$$ \mathfrak{E}\!\left(e;t\right)=\iiint {f}_{\Theta (t)}\left(\theta (t)\right){f}_{H(t)}\left(h(t)\right){f}_{\zeta_{ei}(t)\mid H(t)}\left({\varepsilon}_{ei}(t)|h(t)\right)\mathcal{L}\left({\theta}_{\textrm{true}}(t),h(t),{\varepsilon}_e(t);t\right)\ d\theta (t) dh(t)d{\varepsilon}_e(t). $$

(14.6)

Finally, the aggregate expected risk of sensor bias over the life cycle is given as:

$$ {\mathfrak{E}}_{\textrm{LC}}(e)={\int}_{\Omega_T}\mathfrak{E}\left(e;t\right)\ dt={\sum}_{k=1}^{t_k\in {\Omega}_T}\mathfrak{E}\!\left(e;{t}_k\right). $$

(14.7)

We obtain the optimal sensor design e^∗ using ${\mathfrak{E}}_{\textrm{LC}}(e)$ as the objective functional by deploying the Bayesian optimization algorithm described in Yang et al. [1, 2], such that:

$$ {e}^{\ast }=\underset{e}{\textrm{argmin}}{\mathfrak{E}}_{\textrm{LC}}(e) $$

(14.8)

14.4 Results

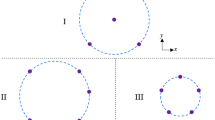
Figure 14.1 shows the optimal sensor network design e^∗ obtained using Eq. (14.8) and the optimization algorithm delineated in Yang et al. [1, 2].

Fig. 14.1

Miter gate and the optimal sensor network design for ${\mu}_{n_{ei}(t)}={10}^{-4}$ and ${\sigma}_{n_{ei}(t)}=2\times {10}^{-6}$. (a) Rendered front view. (b) Rendered side view

We observe that in the reliability-focused design there are more sensors above the mean downstream water head than the number of sensors below it. This is because the probability of sensors malfunctioning is higher when they are located below the mean downstream water head (higher likelihood of being in the submerged zone) than when they are installed above the mean water head (higher likelihood of being in the splash zone). The sensors are strategically placed in the gap’s neighborhood allowing for a realistic inference of the gap length and at the same time, collectively, sensors spend a higher average time in the splash zone over the life span of the structure, such that if the submerged sensors malfunction, the sensors in the splash zone can carry the burden of performing acceptable inference over the life cycle of the miter gate.

14.5 Conclusions

This chapter briefly details the mathematical formulation behind a sensor optimization framework with a dual target: (1) the design obtained should lead to damage inference to an acceptable degree of accuracy; (2) the framework must consider all the uncertainties that the system is subjected to and account for the possibility of sensors malfunctioning over time. The reliability-focused designs lead to inference results that are overall reliable, consistent, representative of true gap evolution over time, and hence lead to improved Value of Information relative to random design.