Keywords

11.1 Introduction

For the past several decades, power flow analysis has been used to quantify the vibratory response of structures. It can be used to determine energy transmission paths within an assembly of structures and allow for design changes to be made to the structure so as to reduce vibration amplitude. Several studies address calculating power flow from experimental measurements [1,2,3,4,5,6] or numerical data output from finite element models [7,8,9,10,11,12]. However, these studies focus on the calculation of power flow, not how it responds to structural modifications. Understanding how power flow changes in response to structural modifications is useful in the context of vibration reduction, particularly in an experimental setting where frequency response functions (FRFs) can readily be measured.

Previous analyses have been proposed for calculating the sensitivity of power flow to changes made in the impedance matrix of a passive receiver structure [13]. This was done by considering the source and receiver as independent substructures that were coupled using the Lagrange multiplier frequency-based substructuring (LMFBS) method and differentiating the power flow equation with respect to the receiver impedance. This approach is valid for numerically modeled structures where the translational and rotational interface degrees of freedom (DOFs) are fully defined, and the meshes on the two interfaces are compatible. In the context of experimental substructuring, where measurement of the rotational DOFs can be difficult, they must be obtained using some approximation. The virtual point transformation (VPT) has been a topic of recent research in the experimental substructuring community [14,15,16,17] and will be used here to extend the general power flow sensitivity equations to equations that can be applied to experimental data.

The VPT accounts for rotational DOFs on the interface of a substructure by using a first-order approximation from measured responses using a set of non-collinear triaxial accelerometers placed in the vicinity of the coupling interface [14]. The interface dynamics are determined in a least-squares sense by projecting a large number of force and response measurements onto a virtual point containing three translational and three rotational DOFs. Larger sets of virtual point coordinates can be obtained, such as shear and torsion deformations, so as to relax the condition of assuming a locally rigid interface [18]. The equations presented here are not dependent on the number of virtual point coordinates that are present. Rather, the number of measurements required to accurately estimate those coordinates changes while the mathematics remains the same.

A quick summary of the VPT is first presented with its underlying assumptions. The experimental power flow sensitivity equations are then derived starting from the virtual point power flow equation. Several assumptions regarding the symmetry of the mobility matrices are made, and the ramifications of these assumptions are discussed. Quality indicators relevant to the assumptions are then presented, and the validity of the sensitivity equations is demonstrated on a numerical model so as to be free of potential experimental measurement errors.

11.2 Virtual Point Transformation

A vast literature pertaining to the VPT exists, but its basic properties will be discussed here as they are required for the derivation of the experimental power flow sensitivity equations. Defining the interface dynamics of a substructure is difficult in an experimental setting because making direct measurements of rotational DOFs is either impractical or impossible. As such, FRFs can be measured in the vicinity of the interface of a substructure and projected onto a virtual point containing three translational and three rotational DOFs. The measured forces and responses used for constructing the FRF matrix do not need to be collocated. That is, the forces and responses do not need to be measured at the same locations or in the same directions near the coupling interface. In fact, to accurately model the interface dynamics using the VPT, the interface must only be locally rigid, and more than six responses and forces must be measured on the structure. The reason for this becomes apparent when looking at the projection from physical to virtual coordinates:

$$ \textbf{u}={\textbf{R}}_{\textbf{u}}\textbf{q}+\boldsymbol{\upmu} $$
(11.1a)
$$ \textbf{m}={\textbf{R}}_{\textbf{f}}^T\textbf{f} $$
(11.1b)

where u and f are the physical response and force vectors, q and m are the virtual point responses and forces, Ru and Rf are the virtual point response and force projection matrices, and μ is a vector containing information regarding the flexibility of the interface. The interface is perfectly rigid when μ = 0. If Nu responses and Nf forces are measured near the interface with a single virtual point containing 6 DOFs, the sizes of Ru and Rf are Nu × 6 and Nf × 6, respectively. So long as Nu and Nu are both greater than 6, Eqs. 11.1a and 11.1b can be solved in a least-squares sense. The transpose of the force projection matrix is used because the virtual point forces cannot be uniquely defined from an arbitrary set of physical forces. Information regarding the structure of these matrices can be found in [14]. Transforming from physical to virtual coordinates requires solving Eqs. 11.1a and 11.1b for q and f. Doing so results in

$$ \textbf{q}={\left({\textbf{R}}_{\textbf{u}}^T{\textbf{R}}_{\textrm{u}}\right)}^{-\textbf{1}}{\textbf{R}}_{\textbf{u}}^T\textbf{u} $$
(11.2a)
$$ \textbf{f}={\textbf{R}}_{\textbf{f}}{\left({\textbf{R}}_{\textbf{f}}^T{\textbf{R}}_{\textbf{f}}\right)}^{-1}\textbf{m} $$
(11.2b)

where the residual μ is no longer present because it is orthogonal to \( {\textbf{R}}_{\textbf{u}}^T \). These matrices only act on the interface DOFs, but physical internal DOFs can be retained as well by augmenting the pseudo-inverses with identify matrices equal to the size of the number of measured internal responses and forces given by

$$ {\textbf{T}}_{\textbf{u}}=\left[\begin{array}{cc}{\textbf{I}}_{\textbf{u}}& \textbf{0}\\ {}\textbf{0}& {\left({\textbf{R}}_{\textbf{u}}^T{\textbf{R}}_{\textbf{u}}\right)}^{-\textbf{1}}{\textbf{R}}_{\textbf{u}}^T\end{array}\right] $$
(11.3a)
$$ {\textbf{T}}_{\textbf{f}}^T=\left[\begin{array}{cc}{\textbf{I}}_{\textbf{f}}& \textbf{0}\\ {}\textbf{0}& {\textbf{R}}_{\textbf{f}}{\left({\textbf{R}}_{\textbf{f}}^T{\textbf{R}}_{\textbf{f}}\right)}^{-1}\end{array}\right] $$
(11.3b)

which can now be applied to the experimentally obtained FRF matrices. Since power is most easily calculated with the mobility matrix, the FRFs considered in this work are mobilities, and the terms will be used interchangeably.

Unlike numerical data, the experimental mobility matrix is not guaranteed to be square and symmetric because it is often infeasible to measure forces and responses at the same locations on the structure. As such, the rectangular mobility matrix

$$ {\textbf{Y}}_{\textrm{exp}}=\left[\begin{array}{cc}{\textbf{Y}}_{\textrm{ii}}& {\textbf{Y}}_{\textrm{ic}}\\ {}{\textbf{Y}}_{\textrm{ci}}& {\textbf{Y}}_{\textrm{cc}}\end{array}\right] $$
(11.4)

is available where the subscripts i and c denote internal and coupling interface DOFs, respectively, Yii and Ycc are not required to be square and symmetric, and as a result \( {\textbf{Y}}_{\textrm{ic}}\ne {\textbf{Y}}_{\textrm{ci}}^T \). The coupling interface FRFs can be made square and (possibly) symmetric by applying the VPT matrices

$$ \textbf{Y}={\textbf{T}}_{\textbf{u}}{\textbf{Y}}_{\textrm{exp}}{\textbf{T}}_{\textbf{f}}^T=\left[\begin{array}{cc}{\textbf{Y}}_{\textrm{ii}}& {\textbf{Y}}_{\textrm{iv}}\\ {}{\textbf{Y}}_{\textrm{vi}}& {\textbf{Y}}_{\textrm{vv}}\end{array}\right] $$
(11.5)

where the subscript v denotes a quantity pertaining to the virtual point coordinates. The resulting mobility matrix Y is still not required to be square and symmetric, but the virtual points enforce displacement compatibility between substructure interfaces automatically, and the coupling force can be predicted easily using the LMFBS. The LMFBS method couples FRFs obtained from independent structures using their respective interface FRFs. This is achieved by using a Boolean interface mapping matrix, which identifies the interface DOFs in the global FRF matrix, and calculates the coupling forces between structures explicitly. As only the coupling force is needed for the sensitivity equations, the discussion of the LMFBS will conclude here. However, information on this method can be found in [19, 20], and it is recommended the unfamiliar reader review these references before continuing. Assuming no external forces are applied to the receiver aside from those imparted on it by the source, the coupling force is given by

$$ {\boldsymbol{\uplambda}}_{\textrm{v}}={\left({\textbf{Y}}_{\textrm{v}\textrm{v}}^{\left(\textrm{s}\right)}+{\textbf{Y}}_{\textrm{v}\textrm{v}}^{\left(\textrm{r}\right)}\right)}^{-1}{\textbf{B}}_{\textbf{u}}^{\left(\textrm{s}\right)}{\textbf{Y}}^{\left(\textrm{s}\right)}\textbf{m} $$
(11.6)

where the superscripts (s) and (r) denote source and receiver properties, respectively, and \( {\textbf{B}}_{\textbf{u}}^{\left(\textrm{s}\right)} \) is a Boolean interface mapping matrix that identifies the interface (virtual) DOFs on the source based on measured internal responses. Another interface mapping matrix exists for forces. In an arbitrary structure, the response and force interface mapping matrices take the form

$$ {\textbf{B}}_{\textbf{u}}=\left[{\textbf{0}}_{\textbf{u}}\kern0.5em \pm \textbf{I}\right] $$
(11.7a)
$$ {\textbf{B}}_{\textbf{f}}=\left[\begin{array}{cc}{\textbf{0}}_{\textbf{f}}& \pm \textbf{I}\end{array}\right] $$
(11.7b)

where I is the identity matrix of size 6Nv for Nv virtual points, 0u and 0f are (in general) rectangular zero matrices where the number of columns in each matrix is determined by the number of internally measured responses or forces, respectively. The positive and negative identity matrices are required to enforce compatibility at the substructure interfaces. That is, if the source interface mapping matrix uses I, then the receiver interface mapping matrix must use −I.

11.3 Experimental Power Flow Sensitivity

Using the quantities derived in the previous section, power flow through an interface whose dynamics are defined by a virtual point can now be calculated as

$$ Q=\frac{1}{2}{\boldsymbol{\uplambda}}_{\textrm{v}}^H{\textbf{Y}}_{\textrm{v}\textrm{v}}^{\left(\textrm{r}\right)}{\boldsymbol{\uplambda}}_v $$
(11.8)

The power flow sensitivity equations are derived by differentiating Eq. 11.8 with respect to the receiver impedance. This allows one to determine how power flow from source to receiver will change due to small modifications made to the receiver structure. This can be done using the chain rule

$$ \frac{\partial Q}{\partial {{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)}}=\frac{\partial Q}{\partial {\textbf{Y}}_{\textrm{vv}}^{\left(\textrm{r}\right)}}\frac{\partial {\textbf{Y}}_{\textrm{vv}}^{\left(\textrm{r}\right)}}{\partial {{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)}} $$
(11.9a)
$$ \frac{\partial Q}{\partial {{\boldsymbol{\grave{Z}}}}^{{\left(\textrm{r}\right)}^H}}=\frac{\partial Q}{\partial {\textbf{Y}}_{\textrm{vv}}^{{\left(\textrm{r}\right)}^H}}\frac{\partial {\textbf{Y}}_{\textrm{vv}}^{(r)^H}}{\partial {{\boldsymbol{\grave{Z}}}}^{{\left(\textrm{r}\right)}^H}} $$
(11.9b)

where \( {{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)} \) is the receiver impedance. The \( {\grave{\circ} } \) notation is used because the actual receiver impedance is not known as it cannot be determined by inverting the experimentally determined mobility matrix due to the possibility of non-collocated internal DOF measurements Yii. It will be shown that these measurements are not actually needed in the calculation of the sensitivity equations, and as a result power is instead differentiated with respect to a “synthetic” impedance where internal FRFs are assumed to be collocated. This will become more apparent later in the derivation. First, evaluating the derivatives of power with respect to the virtual point mobility and its complex conjugate is done by applying the chain and product rule to Eq. 11.8. Doing so results in

$$ \frac{\partial Q}{\partial {\textbf{Y}}_{\textrm{v}\textrm{v}}^{\left(\textrm{r}\right)}}=-\frac{1}{2}\left(\textbf{I}-{\textbf{Z}}_{\textrm{v}\textrm{v}}^{\left(\textrm{c}\right)}{\textbf{Y}}_{\textrm{v}\textrm{v}}^{\left(\textrm{r}\right)}\right){\textbf{G}}_{\lambda_{\textrm{v}}{\lambda}_{\textrm{v}}}^T $$
(11.10a)
$$ \frac{\partial Q}{\partial {\textbf{Y}}_{\textrm{v}\textrm{v}}^{{\left(\textrm{r}\right)}^H}}=\frac{1}{2}{\textbf{G}}_{\lambda_{\textrm{v}}{\lambda}_{\textrm{v}}}^T{\textbf{Y}}_{\textrm{v}\textrm{v}}^{\left(\textrm{r}\right)}{\textbf{Z}}_{\textrm{v}\textrm{v}}^{{\left(\textrm{c}\right)}^H} $$
(11.10b)

where \( {\textbf{Z}}_{\textrm{vv}}^{\left(\textrm{c}\right)}={\left({\textbf{Y}}_{\textrm{vv}}^{\left(\textrm{s}\right)}+{\textbf{Y}}_{\textrm{vv}}^{\left(\textrm{r}\right)}\right)}^{-1} \) is the coupling impedance, and \( {\textbf{G}}_{\lambda_{\textrm{v}}{\lambda}_{\textrm{v}}}={\boldsymbol{\uplambda}}_{\textrm{v}}{\boldsymbol{\uplambda}}_{\textrm{v}}^H \) is the one-sided coupling force cross-spectral density matrix. Again, it was assumed that the virtual point mobilities were symmetric in this calculation. The task at hand now is to calculate the second set of derivatives in Eqs. 11.9a and 11.9b. Doing so requires defining an analytical relationship between the interface mobility and global impedance matrix of the receiver. Fortunately, this can be done using

$$ {\textbf{Y}}_{\textrm{vv}}^{\left(\textrm{r}\right)}={\textbf{B}}_{\textbf{u}}^{\left(\textrm{r}\right)}{\textbf{Y}}^{\left(\textrm{r}\right)}{\textbf{B}}_{\textbf{f}}^{{\left(\textrm{r}\right)}^T} $$
(11.11)

where the structure of the mobility matrix Y(r) is given in Eq. 11.5. The internal mobility Yii matrix has not yet been constrained to be square and symmetric, and as a result equating the impedance matrix to be the inverse of the mobility matrix cannot be done because the experimental mobility matrix could be singular. However, consider for a moment an experimental mobility matrix in which the interface DOFs have been projected onto virtual coordinates, and the internally measured FRFs were collocated, making Yii square and symmetric. To distinguish between this hypothetical set of internal FRFs and the actual measured ones, the following notation will be adopted:

$$ {{\boldsymbol{\grave{Y}}}}^{\left(\textrm{r}\right)}=\left[\begin{array}{cc}{{\boldsymbol{\grave{Y}}}}_{\textrm{ii}}& {\textbf{Y}}_{\textrm{iv}}\\ {}{\textbf{Y}}_{\textrm{vi}}& {\textbf{Y}}_{\textrm{vv}}\end{array}\right] $$
(11.12)

where \( {{\boldsymbol{\grave{Y}}}}_{\textrm{ii}} \) is set of hypothetically collocated internal FRFs, and due to the assumed symmetry of Yvv, \( {\textbf{Y}}_{\textrm{iv}}={\textbf{Y}}_{\textrm{vi}}^T \). The implication of this is that (1) the force and response interface mapping matrices are identical, and (2) the mobility matrix is invertible – the receiver impedance matrix mathematically exists. That is,

$$ {\textbf{B}}^{\left(\textrm{r}\right)}={\textbf{B}}_{\textbf{u}}^{\left(\textrm{r}\right)}={\textbf{B}}_{\textbf{f}}^{\left(\textrm{r}\right)}=\left[\begin{array}{cc}\textbf{0}& \pm \textbf{I}\end{array}\right] $$
(11.13)

and

$$ {{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)}={{\boldsymbol{\grave{Y}}}}^{{\left(\textrm{r}\right)}^{-1}} $$
(11.14)

is the “synthetic” impedance. From these two statements, Eq. 11.11 can be rewritten as

$$ {\textbf{Y}}_{\textrm{vv}}^{\left(\textrm{r}\right)}={\textbf{B}}^{\left(\textrm{r}\right)}{{\boldsymbol{\grave{Z}}}}^{{\left(\textrm{r}\right)}^{-1}}{\textbf{B}}^{{\left(\textrm{r}\right)}^T} $$
(11.15)

where \( {{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)} \) exists only in a mathematical sense and is not a matrix that is obtained from experimental measurements. While this may seem troublesome at first, it will be shown that the internal mobility matrix does not explicitly appear in the sensitivity equations, and are therefore not needed. Now that a relationship between the interface mobility and impedance matrix of the receiver exists, differentiation gives

$$ \frac{\partial {\textbf{Y}}_{\textrm{vv}}^{\left(\textrm{r}\right)}}{\partial {{\boldsymbol{\grave{Z}}}}^{(r)}}=-{\overline{\boldsymbol{\grave{Y}}}}\otimes {{\overline{\boldsymbol{\grave{Y}}}}}^T $$
(11.16a)
$$ \frac{\partial {\textbf{Y}}_{\textrm{vv}}^{{\left(\textrm{r}\right)}^H}}{\partial {{\boldsymbol{\grave{Z}}}}^{{\left(\textrm{r}\right)}^H}}=-{{\overline{\boldsymbol{\grave{Y}}}}}^{\ast}\otimes {{\overline{\boldsymbol{\grave{Y}}}}}^H $$
(11.16b)

where \( {\overline{\boldsymbol{\grave{Y}}}}={\textbf{B}}^{\left(\textrm{r}\right)}{{\boldsymbol{\grave{Y}}}}^{\left(\textrm{r}\right)}=\left[\begin{array}{cc}{\textbf{Y}}_{\textrm{vi}}& {\textbf{Y}}_{\textrm{vv}}\end{array}\right] \), and ⊗ is the Kronecker product. As such, Eqs. 11.16a and 11.16b are fourth-order tensors. The hypothetical internal FRF matrix \( {{\boldsymbol{\grave{Y}}}}_{\textrm{ii}} \) is not present in this derivative, and therefore does not actually need to be measured experimentally to calculate the power flow sensitivities. The only FRFs that need to be measured are the interface mobilities to be projected onto a virtual point, and the mobilities that couple the internal and interface dynamics Yvi. This matrix is determined by applying forces to the internal DOFs and measuring the response at the interface. Alternatively, due to reciprocity in Eq. 11.12, Yiv can be determined by applying forces to the interface and measuring the response at several internal DOFs, and its transpose can be used in place of Yvi. The derivatives of power with respect to the receiver impedance are then written as

$$ \frac{\partial Q}{\partial {{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)}}=\frac{1}{2}\left(\textbf{I}-{\textbf{Z}}_{\textrm{v}\textrm{v}}^{\left(\textrm{c}\right)}{\textbf{Y}}_{\textrm{v}\textrm{v}}^{\left(\textrm{r}\right)}\right){\textbf{G}}_{\lambda_{\textrm{v}}{\lambda}_{\textrm{v}}}^T\left[{\overline{\boldsymbol{\grave{Y}}}}\otimes {{\overline{\boldsymbol{\grave{Y}}}}}^T\right] $$
(11.17a)
$$ \frac{\partial Q}{\partial {{{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)}}^H}=-\frac{1}{2}{\textbf{G}}_{\lambda_{\textrm{v}}{\lambda}_{\textrm{v}}}^T{\textbf{Y}}_{\textrm{v}\textrm{v}}^{\left(\textrm{r}\right)}{\textbf{Z}}_{\textrm{v}\textrm{v}}^{\left(\textrm{c}\right)}\left[{{\overline{\boldsymbol{\grave{Y}}}}}^{\ast}\otimes {{\overline{\boldsymbol{\grave{Y}}}}}^H\right] $$
(11.17b)

where the derivatives of Q are given with respect to the synthetic receiver impedance \( {{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)} \) using the LTI assumption of a reciprocal mobility matrix. This means that information about how power flow will change due to modifications made to the internal DOFs of the receiver is known, even without measuring the internal mobility matrix directly. All that is needed is a set of FRFs from the interface to a desired number of internal DOFs to calculate Eqs. 11.17a and 11.17b. One final step is needed to calculate the power flow sensitivities. As is, Eqs. 11.17a and 11.17b are complex valued matrices, which is not of much use when trying to determine how the real part of power flow changes with respect to the real (dissipative) and imaginary (elastic and inertial) components of the receiver impedance. Additionally, active power (the real component of power) is usually of interest because it describes the energy that is moving within the structure. Derivatives relating the real component of Q to the real and imaginary components of the receiver impedance can be obtained by applying the properties of the Wirtinger derivatives to Eqs. 11.17a and 11.17b [21]. Doing so results in

$$ {\textbf{S}}_{\textrm{R}}=\frac{\partial \operatorname{Re}\left\{Q\right\}}{\partial \operatorname{Re}\left\{{{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)}\right\}}=\operatorname{Re}\left\{\frac{\partial Q}{\partial {{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)}}\right\}+\operatorname{Re}\left\{\frac{\partial Q}{\partial {{{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)}}^H}\right\} $$
(11.18a)
$$ {\textbf{S}}_{\textrm{I}}=\frac{\partial \operatorname{Re}\left\{Q\right\}}{\partial \operatorname{Im}\left\{{{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)}\right\}}=-\operatorname{Im}\left\{\frac{\partial Q}{\partial {{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)}}\right\}+\operatorname{Im}\left\{\frac{\partial Q}{\partial {{{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)}}^H}\right\} $$
(11.18b)

where Re{∘} and Im{∘} denote the real and imaginary components of the argument, respectively. The resulting matrices, termed the real and imaginary sensitivities, are both real valued, square, and symmetric. They describe how power flow changes with respect to small modifications made to the real and imaginary components of the receiver’s impedance at a single DOF (diagonal elements) or the coupling between two DOFs (off-diagonal elements).

11.4 Quality Indicators

One quality indicator will be used to determine the accuracy of the VPT. Numerical data is used here to avoid measurement error in the projection matrices and FRFs. Since the sensitivity equations assume a symmetric mobility matrix, particularly the virtual point partition of the mobility matrix, the first indicator of measurement quality is the coherence function. It is defined as

$$ {\chi}_{\textrm{mn}}=\frac{\left({Y}_{\textrm{mn}}+{Y}_{\textrm{nm}}\right)\left({Y}_{\textrm{mn}}^{\ast }+{Y}_{\textrm{nm}}^{\ast}\right)}{2\left({Y}_{\textrm{mn}}{Y}_{\textrm{mn}}^{\ast }+{Y}_{\textrm{nm}}{Y}_{\textrm{nm}}^{\ast}\right)} $$
(11.19)

which compares how similar the FRFs Ymn and Ynm are. It outputs a real valued number χmn between 0 and 1, with 0 indicating the two FRFs are dissimilar, and 1 indicating the two FRFs are identical. The diagonal elements of the matrix are guaranteed to have a value of 1. A Hermitian matrix, for example, would be the identity matrix. If the matrix of FRFs is symmetric, the resulting coherence matrix would be a matrix containing all ones.

Another quality indicator to describe how well the VPT estimates the interface dynamics is passivity. Since a mobility matrix is being used in the sensitivity equations, the phase of the drive-point FRFs should be between ±90∘. This indicator is used to verify that the structure does not generate its own energy. Other quality indicators exist, such as force and response consistency, which describe the rigidity of the coupling interface. While it is important to calculate these quantities to ensure the VPT is a valid coupling procedure in a specific frequency range, it will not be further discussed here. The reason for this is because it has been verified in a previous study that the model considered in the case study presented here has a consistency of 1 over the entire frequency range tested and was verified by the authors to be passive [22]. More information on this quality indicator can be found in [14, 15].

11.5 Case Study: Complex Conjugate Impedance

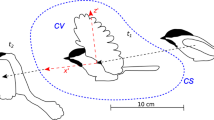
To demonstrate that the virtual point sensitivity equations are valid, and do in fact calculate the rate of change of power flow with respect to the receiver impedance, a source structure coupled to a receiver whose impedance is complex conjugate to that of the source is considered. This example was chosen because it is known that power flow is maximized when a source is connected to its complex conjugate [23] – the quantity being aptly named the maximum available power (MAP) in the literature. Therefore, given that SR and SI are derivatives of power with respect to the receiver impedance, both should be equal to the zero matrix at all frequencies when the receiver impedance is the complex conjugate of the source impedance. A simple beam structure is considered with one coupling interface, requiring a single virtual point, shown in Fig. 11.1. Several FRFs from the virtual point to internal DOFs are shown as well.

Fig. 11.1
A three-dimensional model of the simple beam structure indicates a virtual point, forces, and responses.

Virtual point location and measurement locations for constructing \( {\overline{\boldsymbol{\grave{Y}}}} \) using internal force and response measurements, resulting in interface mapping matrices Bf and Bu, respectively

Full size image

Figure 11.1 provides a visual intuition of how the matrix \( {\overline{\boldsymbol{\grave{Y}}}} \) can be obtained based on internally measured forces or responses. The purpose of including internal DOFs in the analysis is to provide information to the analyst regarding which locations on the structure, specifically those away from the interface, to modify in an effort to reduce power flow. These internal DOFs can be measured by means of forces or responses, as all that is needed for the sensitivity equations are the transfer mobilities from the virtual point to the desired internal DOFs. Practically speaking, if the sensitivity at a few locations internal to the structure is of interest, measuring the response at these internal locations with accelerometers due to excitations at the interface is a feasible task. When a higher spatial resolution of the sensitivity on the internal DOFs is desired, it becomes more practical to apply forces to the DOFs of interest and measure the response at the interface.

Analysis was performed over the range of 60–1600 Hz. The beam being analyzed was made out of aluminum with a modulus of elasticity of 69 GPa, density of 2700 kg/m3, and Poisson’s ratio of 0.33. It had a nominal length of 38.1 cm (15 in.), width of 3.81 cm (1.5 in.), and thickness of 1.9 cm (0.75 in.). The base of the beam was flanged to allow for it to be bolted to another structure. The depth of this flange was 3.81 cm with a thickness of 1.9 cm, and there was a bolt hole at the center with a diameter of 1.33 cm. This is where the virtual point was located for substructure coupling. These dimensions provided sufficient stiffness in the vicinity of the coupling interface (flange) to yield a consistency of 1 over the frequency range of interest.

This example is not physical as coupling a source to its complex conjugate is not realizable. However, it does serve to demonstrate that Eqs. 11.17a and 11.17b are the analytical derivatives of power flow with respect to the receiver impedance, as well as the fact that they are indifferent to using internal force or response measurements. Additionally, the assumption of a reciprocal virtual point mobility, and its effect on the resulting sensitivities, can be examined through this demonstration. This was done by projecting FRFs obtained from a numerical model onto the virtual point in two ways. The first is more representative of an experimental setup, in which the forces applied and responses measured on the interface are not collocated – the forces and responses are not measured at the same location. The second guarantees symmetry of the virtual point mobility matrix by collocating for forces and responses on the interface, resulting in identical transformation matrices Tu and Tf. Non-collocated virtual point interface force and response measurements are shown in Fig. 11.2a, and collocated interface measurements are shown in Fig. 11.2b.

Fig. 11.2
Two three-dimensional L-shaped models of the interface of the beam structure labeled a and b indicate the non-collocated and collected forces and responses.

Applied forces and measured responses on interface of beam structure for (a) non-collocated force and response measurements and (b) collocated force and response measurements

Full size image

11.6 Results

The symmetry of the virtual point mobility for non-collocated and collocated interface measurements is first compared as the symmetry will affect the resulting calculation of power flow sensitivity. The frequency-averaged coherence of \( {\textbf{Y}}_{\textrm{vv}}^{\left(\textrm{r}\right)} \) is shown in Fig. 11.3. It is clear from the low coherence on the off-diagonal terms that the virtual point interface mobility matrix is not symmetric over most of the frequency range. In other words, the virtual point does not behave reciprocally as would a node in a typical linear finite element model. Based on the data shown in Fig. 11.3a, applying a force in the x direction and measuring the velocity in the θx direction is not the same applying a force in the θx direction and measuring the velocity in the x direction. This is an issue particularly when substituting these results into Eqs. 11.17a and 11.17b because of the symmetry that was assumed in deriving the equations. Symmetry of the virtual point mobility is preserved for the collocated interface measurements, which is indicated by a coherence of 1 for all FRFs.

Fig. 11.3
2 matrixes. a and b. The matrixes of D O F versus D O F have 6 columns and 6 rows. The row and column headings are x, y, z, theta subscript x, theta subscript y, and theta subscript z. The matrices indicate the range from 0 to 1 using color codes on the right side.

Frequency-averaged coherence of virtual point mobility \( {\boldsymbol{Y}}_{\textrm{vv}}^{\left(\textrm{s}\right)} \) for (a) non-collocated force and response measurements and (b) collocated force and response measurements

Full size image

Now that it is known that the non-collocated interface measurements result in an asymmetric virtual point mobility, a comparison between the calculated power flow and its corresponding sensitivities is shown in Fig. 11.4. More specifically, the sensitivity of the z component of the virtual point mobility matrix is shown. This value describes how power flow would respond to the changes made to the receiver impedance in the vicinity of the coupling interface in the z direction. Knowing that the values of SR and SI should be zero for all frequencies in this coupling configuration, there is clearly an issue with the sensitivity calculated from the non-collocated interface measurements. At 60 Hz, the magnitude of the real sensitivity is on the order of 102 and the imaginary sensitivity is on the order of 103. As frequency increases, the values of the sensitivities decrease, but only to a magnitude of approximately 10−7. Lastly, there is a discrepancy between the predictions in the real and imaginary sensitivities using internal response and internal force measurements. This again is due to the asymmetry in the virtual point mobility matrix.

Fig. 11.4
2 graphs a and b. The graphs of power and sensitivity versus frequency for map and S subscript R and S subscript I from B power r subscript u and B power r subscript f.

Power flow and real and imaginary sensitivities of z coordinate of virtual point with different sets of internal DOFs for (a) non-collocated force and response measurements, and (b) collocated force and response measurements

Full size image

The collocated interface measurements result in a real and imaginary sensitivity that are much smaller than the ones predicted from the non-collocated measurements. At 60 Hz, the values of the real and imaginary sensitivities are on the order of 10−13 and 10−9, respectively – much closer to zero than for the non-collocated measurements. Numerically, given that the sensitivities represent the rate of change in power flow with respect to the real and imaginary impedances, these magnitudes are essentially zero, thus verifying Eqs. 11.17a and 11.17b are the analytical derivatives of power with respect to the receiver impedance. The sensitivities calculated using internal responses and internal forces are approximately identical, though given how close to machine precision the values are it is difficult to compare the two quantities. The spectrum appears noisy due to the small magnitude of the real and imaginary sensitivities. One interesting feature that appears is the apparent resonance at 600 Hz. This coincides with a natural frequency of the source structure when it is uncoupled from any receiver.

One final observation from Fig. 11.4 is that power flow appears to be unaffected by the asymmetry in the virtual point mobility matrix as the frequency dependence of power flow is identical for the non-collocated and collocated interface measurement cases. This is most likely due to the type of coupling considered, where the receiver impedance is complex conjugate that of the source. The resulting coupling interface impedance \( {\textbf{Z}}_{\textrm{vv}}^{\left(\textrm{c}\right)} \) is purely real and does not display resonant behavior as a function of frequency. If a different coupling case were considered, for example, when the receiver impedance is equal to that of the source, the power flow spectrum for the non-collocated and collocated interface measurements should be different. This is shown in Fig. 11.5.

Fig. 11.5
A line graph of power in watts versus frequency in hertz for non-collocated V P T and collocated V P T. The values of the curves are both increasing and decreasing trends.

Power flow for non-collocated and collocated interface measurements for coupling case when \( {{\boldsymbol{\grave{Z}}}}^{\left(\textrm{r}\right)}={{\boldsymbol{\grave{Z}}}}^{\left(\textrm{s}\right)} \)

Full size image

There are some clear discrepancies between power flow calculated with non-collocated and collocated interface measurements when performing the VPT. Capturing resonant frequencies does not appear to be an issue. This is expected as the imaginary component of impedance is fairly small here and the real component dominates similar to what happens when calculating the MAP in Fig. 11.4. The most notable differences in the spectra occur around 200 Hz and 1100 Hz. At 200 Hz, the non-collocated interface measurements dictate that power flow will be negative. This is physically impossible as the interface mobility matrix should be positive semi-definite. At 1100 Hz, the non-collocated VPT appears to create an additional resonant frequency of the assembled structures. This is important to note as power flow is also heavily dependent on the symmetry of the virtual point mobility matrix. Given that there are more matrix multiplication operations in the sensitivity equations, any deviations from a symmetric interface mobility matrix will be further amplified in the calculation of the real and imaginary sensitivities. As is, more research should be done on how to obtain a more symmetric interface mobility matrix so power flow, and the real and imaginary sensitivities, can be more accurately calculated for experimentally obtained mobility data.

11.7 Conclusion

The analytical derivatives of complex power flow from source to passive receiver were derived for experimental data using the VPT to model the dynamics of the coupling interface between substructures. It was shown that the power flow sensitivity can be calculated at internal DOFs using either internally measured forces or responses under the assumption that the receiver mobility matrix is symmetric, without actually measuring the full mobility matrix. This creates a “synthetic” impedances, whose power flow is differentiated with respect to. The equations were tested on a beam structure such that the source was coupled to a receiver whose impedance was the complex conjugate of the source’s. Due to maximum power flow occurring in this coupling configuration, the real and imaginary sensitivities were verified to be zero. However, both power flow and the sensitivities were shown to be dependent on the symmetric mobility assumption as an asymmetric virtual point mobility matrix can lead to spurious resonances in the power flow response and lead to further errors in the calculation of the real and imaginary sensitivities. Future work should apply these equations to experimental data and focus on finding methods to obtain a more symmetric virtual point mobility matrix.