Continuous Sub-prevalent Co-location Pattern Mining

Abstract

Spatial co-location pattern represents a subset of spatial features whose instances are frequently located together in space. Sub-prevalent co-location pattern mining discovers patterns with richer spatial relationships based on star instance model instead of clique instance model. Further, discovering spatiotemporal sub-prevalent co-location pattern is important to reveal the spatiotemporal interaction between spatial features and promote the application of patterns. However, the methods for mining spatiotemporal sub-prevalent co-location pattern measure the interestingness of patterns by the frequency of patterns in time slice set, and ignore the duration of patterns which is an important spatiotemproal information in patterns. Thus, this paper presents mining spatiotemporal sub-prevalent co-location pattern by considering the duration and the frequency of patterns. Specifically, a novel pattern, is proposed by defining the continuous sub-prevalent index. Then, an efficient algorithm is designed to mine the proposed patterns by utilizing the anti-monotonicity of continuous sub-prevalent index to prune unpromising patterns. Extensive experiments on synthetic and real datasets verify the practicability of the proposed patterns and the effectiveness of the proposed algorithm.

1 Introduction

With the rapid development of spatial information technology such as the global positioning system, spatial data has shown an explosive growth. Spatial co-location pattern mining is an important branch of spatial data mining, which has draw the attention of researchers due to practicality of co-location patterns in environmental protection [1], public security [2] and public health [3]. A prevalent co-location pattern is a subset of spatial features whose instances are frequently collocated within a neighbourhood. For example, that Egyptian Plover occur frequently in near Nile Crocodile can be expressed as a prevalent co-location pattern {Egyptian Plover, Nile Crocodile}.

Prevalent co-location pattern mining determines the neighbor relationship of spatial instances through the distance threshold, generates all row instances of patterns based on clique instance model(i.e., a row instance forms a clique), calculates the participation indices of patterns on the basis of row instances, and finally discovers all prevalent patterns through the participation index threshold [4]. In order to capture richer spatial relationships, sub-prevalent co-location pattern and star participation index based on star instance model are proposed, which loosen the clique constraint of spatial instances in a row instance.

Both prevalent co-location pattern and sub-prevalent co-location pattern ignore the time factor of patterns, i.e., patterns vary with time. For example, seagulls migrate to lakes in Yunnan to spend the cold winter, and leave from lakes when spring comes. This shows the pattern {Seagull, Lake} change with the season.

Fig. 1.

The distribution of co-location patterns in time slice set

To mine time-varying patterns, spatiotemporal co-location pattern mining was introduced. Celik et al. [5] mine co-location patterns on each time slice and finds patterns which appear on many time slices. Li et al. [6, 7] mine sub-prevalent co-location patterns existing on many time slices. These spatiotemporal co-location patterns consider the frequency of patterns on time slices. However, besides the frequency of patterns, we argue that the duration of patterns is also important. Let us see Fig. 1. The frequencies of pattern in Fig. 1(a) and Fig. 1(b) are the same (i.e., 50%), but the duration of pattern in Fig. 1(a) is longer than that in Fig. 1(b). This implies the pattern lasts for a period of time besides repeatedly appearing. This kind of patterns is also meaningful. For instance, instead of passing by, seagulls spending the cold winter on lakes may be more meaningful for environmental protection.

Motivated by the above, we propose continuous sub-prevalent co-location pattern by taking into account the duration and the frequency of sub-prevalent co-location pattern. The main contributions of the paper are as follows:

• We define the continuous sub-prevalent index to measure pattern, and propose the novel continuous sub-prevalent co-location pattern.

• We prove the anti-monotonicity of the proposed measure, and design an efficient algorithm to mine the proposed patterns by utilizing the anti-monotonicity.

• We conduct extensive experiments on real and synthetic data sets. The experimental results show that the proposed pattern is practical and the proposed algorithm is efficient.

The rest of the paper is organized as follows. We review the related work in Sect. 2. Section 3 introduces preliminaries and defines the proposed continuous sub-prevalent co-location pattern. Section 4 describes the algorithm to mine the proposed patterns. Section 5 presents the experimental evaluation and Sect. 6 concludes the paper.

2 Related Work

2.1 Prevalent Co-location Pattern

Huang et al. [4] defined the prevalent co-location pattern based on clique instance model and proposed the Join-based mining algorithm, studies have proposed optimization algorithms [8,9,10,11,12] to solve the low efficiency issues of the Join-based algorithm.

Due to the impact of time factor on the co-location pattern, Celik et al. [5] analyzes the time-varying co-location pattern, and proposed a mixed spatiotemporal MDCOPs algorithm. Andrzejewski and Boinski [13] proposed the MAXMDCOP-Miner algorithm to solve the low efficiency issue of the MDCOPs algorithm. Qian et al. [14] proposed a sliding window model, which introduces the impact of event time intervals into the index to measure the spatiotemporal co-location pattern. Ma et al. [15] proposed a two-step framework to mine evolving pattern over time. Yang and Wang [16] proposed a spatiotemporal co-location congestion pattern mining method to discover the orderly set of roads with congestion propagation in urban traffic.

2.2 Sub-prevalent Co-location Pattern

To mine co-location pattern with richer spatial relationship, Wang et al. [17, 18] proposed the sub-prevalent co-location pattern based on star instance model which loosens the clique constraint of spatial instances in a row instance, and designed the PTBA and PBA algorithms to mine sub-prevalent co-location patterns. Ma et al. [19] proposed the sub-prevalent co-location pattern with dominant feature. Xiong et al. [20] presented mining fuzzy sub-prevalent co-location pattern with dominant feature.

Taking into account the importance of time factor, Li et al. [6, 7] proposed the spatiotemporal sub-prevalent co-location pattern by considering the frequency of pattern.

Distinct from the spatiotemporal sub-prevalent co-location pattern in [6, 7], our proposed continuous sub-prevalent co-location pattern not only considers the frequency of pattern but also the duration of pattern.

3 Preliminaries and Problem Definition

3.1 Spatial Sub-prevalent Co-location Pattern

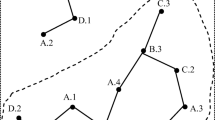
Let $F=\{f_{1},f_{2},...,f_{n}\}$ be the set of spatial features in a spatial dataset, $S=S_{1}\cup S_{2}\cup ... \cup S_{n}$ be the set of spatial instances where $S_i$ is the instance set of $f_i$, and d be a user-specified distance threshold. For two instances $i_i,i_j\in S$, if the Euclidean distance between them satisfies distance$(i_i,i_j)\le d$, they satisfy the neighbor relationship $R(i_i,i_j)$. Figure 2(a) shows a spatial dataset, where $F=\{A,B,C,D\}$, $S=\{A.1,A.2,A.3,B.1,B.2,B.3,C.1,C.2,C.3,D.1,D.2\}$, and the neighbor relationships between instances are expressed by lines. A sub-prevalent co-location pattern c is a subset of the feature set, i.e., $c\subseteq F$, and the number of features in c is called the size k of c, i.e., $k=|c|$. The related definitions of sub-prevalent co-location pattern [17, 18] is as follows.

Definition 1

(Star Neighbodhoods Instance, SNsI). The set of star neighborhoods instances of an instance $i_j\in S$ is defined as $SNsI(i_{j})=\{i_{k}|distance(i_{j},i_{k})\le d,$ $i_{k}\in S$ $\}$.

Definition 2

(Star Participation Instance, SPIns). The star participation instance of a feature $f_i\in c$ is defined as $SPIns(f_{i},c)=\{i_{j}|i_{j}\in f_{i}$ and the feature set of $SNsI(i_{j})$ contains all features in c}.

In Fig. 2(a), $SNsI(A.1)=\{A.1, B.2, C.3\}$, $SPIns(A,\{A, B, C\})=\{A.1, A.2\}$

Fig. 2.

A spatiotemporal dataset with three time slices

Definition 3

(Star Participation Ratio, SPR). The star participation ratio of a feature $f_i\in c$ is defined as the ratio of the number of star participation instances of $f_i$ to the number of instances of $f_i$:

$$\begin{aligned} SPR(f_{i},c)=|SPIns(f_{i},c)|/|S_{i}| \end{aligned}$$

(1)

Definition 4

(Star Participation Index, SPI). The star participation index of a pattern c is defined as the minimum of the star participation rates of all features in c:

$$\begin{aligned} SPI(c)=\mathop {\textrm{min}}_{f_{i}\in c}\{SPR(f_{i},c)\} \end{aligned}$$

(2)

Definition 5

(Sub-prevalent Co-location Pattern, SCP). Given a user-specified star participation index threshold $\theta$, if $SPI(c)\ge \theta$, the pattern c is called a sub-prevalent co-location pattern.

In Fig. 2(a), for a pattern $\{A, B, C\}$, $SPR(A,\{A, B, C\})=0.67$, $SPR(B,\{A, B, C\})=0.67$, $SPR(C,\{A, B, C\})=0.67$ and $SPI(\{A,B,C\})=$ min$\{0.67,0.67,0.67\}=0.67$, if $\theta =0.5$, the pattern $\{A,B,C\}$ is a SCP.

3.2 Continuous Sub-prevalent Co-location Pattern

Distinct from mining sub-prevalent co-location patterns from a spatial dataset, we propose mining continuous sub-prevalent co-location patterns from a spatiotemporal dataset by taking into account the duration and the frequency of patterns.

Let $T=\{t_1, t_2, ..., t_m\}$ be the set of time slices in a spatiotemporal dataset, $F=F^{1}\bigcup F^{2}\bigcup ...\bigcup F^{m}$ be the set of spatial features where $F^{i}=\{f^{i}_{1}, f^{i}_{2}, ..., f^{i}_{n}\}$ is the feature set on time slice $t_i$, $S= S^{1}\bigcup S^{2}\bigcup ...\bigcup S^{m}$ be the set of spatial instances where $S^{i}=S^{i}_{1}\bigcup S^{i}_{2}\bigcup ...\bigcup S^{i}_{n}$ be the instance set on $t_i$ and $S^{i}_{j}$ is the instance set of $f_j$ on $t_i$. Figure 2 shows a spatiotemporal dataset with 3 time slices each of which is Fig. 2(a), Fig. 2(b) and Fig. 2(c) respectively.

We define the related concepts of continuous sub-prevalent co-location pattern as follows.

Definition 6

(Duration time slices, DTS). Given a sub-prevalent co-location pattern c, if it appears on time slice $t_a$, disappears on time slice $t_d$, and keeps on time slices $t_i(t_a\le t_i< t_d)$, then a set of duration time slices DTS(c) of c is defined as:

$$\begin{aligned} DTS(c)=\{t_a,t_{a+1},...,t_{d-1}\} \end{aligned}$$

(3)

Intuitively, a pattern may have multiple sets of duration time slices which can be noted by $DTSs(c)=\{DTS^{1}(c), DTS^{2}(c),..., DTS^{l}(c)\}$.

Definition 7

(Continuous sub-prevalent index, CSI). Given a sub-prevalent co-location pattern c, the continuous sub-prevalent index CSI(c) of c is defined as:

$$\begin{aligned} CSI(c)=\frac{\sum _{i=1}^{|DTSs(c)|}|DTS^{i}(c)|*\frac{|DTS^{i}(c)|}{|T|}}{Non(c)*\frac{1}{|T|}+\sum _{i=1}^{|DTSs(c)|}|DTS^{i}(c)|*\frac{|DTS^{i}(c)|}{|T|}} \end{aligned}$$

(4)

Where $\frac{|DTS^{i}(c)|}{|T|}$ is the weight of duration time slice set $DTS^{i}(c)$ of c, Non(c) is the number of time slices without c, i.e., $Non(c)=|T-\bigcup _{i=1}^{|DTSs(c)|}DTS^{i}(c)|$, and $\frac{1}{|T|}$ is the weight of time slices without c.

Definition 8

(Continuous sub-prevalent co-location pattern, CSCP). Given a sub-prevalent co-location pattern c and a user-specified continuous sub-prevalent index threshold $\rho$, if $CSI(c)\ge \rho$, c is called a continuous sub-prevalent co-location pattern.

In Fig. 2, $T=\{t_1,t_2,t_3\}$, if $\{A, B, C\}$ is a sub-prevalent co-location pattern on time slice $t_1$ and $t_2$, then $DTSs(\{A,B,C\})=\{\{t_1, t_2\}\}$, $CSI(\{A, B, C\})=\frac{2*\frac{2}{3}}{1*\frac{1}{3}+2*\frac{2}{3}}=0.8$. if $\rho =0.5$, then $\{A, B, C\}$ is a CSCP.

Problem Statement. Given a spatiotemporal dataset with the time slice set T, the spatial feature set F, the spatial instance set S, a distance threshold d, a star participation index threshold $\theta$, and a continuous sub-prevalent index threshold $\rho$, continuous sub-prevalent co-location pattern mining is to find all CSCPs that satisfy all thresholds.

4 Mining Algorithm

Starting from size-2 patterns, all CSCPs can be mined level-by-level. To improve the efficiency of the algorithm, the anti-monotonicity of continuous sub-prevalent index will be proven, and be used for pruning unpromising patterns.

Lemma 1

(Anti-monotonicity of continuous sub-prevalent index). Let c, $c^{'}$ be two co-location patterns such that $c\subset c^{'}$, then $CSI(c)\ge CSI(c^{'})$.

Proof

(1) According the anti-monotonicity of star participation index [17, 18], For $\forall t\in T$, $SPI^{t}(c)\ge SPI^{t}(c^{'})$ holds. If $c^{'}$ is a SCP $(SPI^{t}(c^{'})\ge \theta )$, c is also a SCP $(SPI^{t}(c)\ge \theta )$.

(2) Suppose $DTSs(c)=\{DTS^{1}(c),...,DTS^{l}(c)\}$, $DTSs(c^{'})=\{DTS^{1^{'}}(c^{'}),...,DTS^{l^{'}}(c^{'})\}$. According to (1), for $\forall DTS^{i^{'}}(c^{'})\in DTSs(c^{'})$, $\exists DTS^{i}(c)\in DTSs(c)$, $DTS^{i^{'}}(c^{'})\subseteq DTS^{i}(c)$ holds.

Suppose $DTS^{i1^{'}}(c^{'}),...,DTS^{il^{'}}(c^{'})\subseteq DTS^{i}(c)$. For $\forall i1^{'}\le i^{'},j^{'}\le il^{'},i^{'}\ne j^{'}$, $DTS^{i^{'}}(c^{'})\cap DTS^{j^{'}}(c^{'})=\varnothing$ and $\bigcup _{i^{'}=i1^{'}}^{il^{'}}DTS^{i^{'}}(c^{'})\subseteq DTS^{i}(c)$ hold.

Then, we have $\sum _{i^{'}=i1^{'}}^{il^{'}}|DTS^{i^{'}}(c^{'})|^{2}\le |DTS^{i}(c)|^{2}$. Further, we have $\sum _{i=1}^{|DTSs(c^{'})|}|DTS^{i}(c^{'})|^{2}\le \sum _{i=1}^{|DTSs(c)|}|DTS^{i}(c)|^{2}$. On the other hand, we have $Non(c^{'})\ge Non(c)$.

So, we have $\frac{Non(c)}{\sum _{i=1}^{|DTSs(c)|}|DTS^{i}(c)|^{2}}+1$ $\le \frac{Non(c^{'})}{\sum _{i=1}^{|DTSs(c^{'})|}|DTS^{i}(c^{'})|^{2}}+1$, i.e.,

$\frac{\sum _{i=1}^{|DTSs(c)|}|DTS^{i}(c)|^{2}}{Non(c)+\sum _{i=1}^{|DTSs(c)|}|DTS^{i}(c)|^{2}} \ge \frac{\sum _{i=1}^{|DTSs(c^{'})|}|DTS^{i}(c^{'})|^{2}}{Non(c^{'})+\sum _{i=1}^{|DTSs(c^{'})|}|DTS^{i}(c^{'})|^{2}}$. Further, we have

$\frac{\sum _{i=1}^{|DTSs(c)|}|DTS^{i}(c)|*\frac{|DTS^{i}(c)|}{|T|}}{Non(c)*\frac{1}{|T|}+\sum _{i=1}^{|DTSs(c)|}|DTS^{i}(c)|*\frac{|DTS^{i}(c)|}{|T|}}\ge \frac{\sum _{i=1}^{|DTSs(c^{'})|}|DTS^{i}(c^{'})|*\frac{|DTS^{i}(c^{'})|}{|T|}}{Non(c^{'})*\frac{1}{|T|}+\sum _{i=1}^{|DTSs(c^{'})|}|DTS^{i}(c^{'})|*\frac{|DTS^{i}(c^{'})|}{|T|}}$,

i.e., $CSI(c)\ge CSI(c^{'})$.    $\square$

Pruning Strategy 1. If $c\subset c^{'}$ and $CSI(c)<\rho$, then $CSI(c^{'})<\rho$, i.e., c and its all supersets are not CSCPs, and can be pruned.

Based on lemma 1 and pruning strategy 1, we propose an efficient Continuous Sub-prevalent Co-location Pattern Mining Algorithm (CSCPMA) for mining all CSCPs. Generally, the CSCPMA adopts the level-by-level and generation-and-test method. Starting from size-2 patterns, it generates size-k candidate patterns based on size-($k-1$) patterns, and tests size-k candidate patterns to get size-k patterns.

Initialization (Step 1–4): The star neighbors instance set of each spatial instance in each time slice $t\in T$ is generated by Gen_SNsI(). All size-1 patterns, i.e., a subset of F, are the beginning the of the iterations(Step 5–13).

Generating Candidate Patterns and Sub-prevalent Patterns (Step 6–9): Size-k candidate patterns are generated by calling Gen_CCSCP(). In Gen_CCSCP(), size-k candidate patterns are generated based on the set $CSCP_{k-1}$ of size-($k-1$) CSCPs according to Lemma 1 and Pruning Strategy 1. Then, In Gen_SCP(), these candidate patterns are tested for generating size-k SCPs.

Generating Continuous Sub-prevalent Co-location Patterns (Step 10): For each size-k SCP, Gen_CSCP() is called to calculate the continuous sub-prevalent index of the pattern according Definition 7. If the pattern satisfies the threshold $\rho$, it is a size-k CSCP.

The time cost of the CSCPMA mainly are Step 2, Step 8 and Step 10. The time complexity of Step 2 for generating star neighbor instance sets is $O(|T||S^{i}|^{2})$, the time complexity of Step 8 for generating SCPs is $O(|T|\sum \limits _{k=1}|C_{k}||S^{i}_{j}|^{k})$, the time complexity of Step 10 for generating CSCP is $O(|T|\sum \limits _{k=1}|SCP_{k}|)$, where $C_{k}$ is the set of size-k candidate patterns and $SCP_{k}$ is the set of size-k SCPs.

5 Experimental Results and Analysis

In this section, we conduct experiments to evaluate the efficiency of the proposed CSCPMA on synthetic datasets and compare the mining results with the STSCPMA [6, 7] on real datasets.

Datasets. We analyze the patterns by two algorithms on two real datasets and evaluate the efficiency of two algorithms by 11 synthetic datasets. The synthetic datasets are randomly generated according to Poisson distribution with different number of features, the number of instances, the number of time slices or the range. The real datasets include the Tokyo-Checkin containing 14 POI types (features) and 115202 checkin (instances), and the ChicagoCrime dataset containing 19 crime types (features) and 373933 crime events (instances). The datasets are described in Table 1. The default parameters of both algorithms are shown in Table 2.

Environment Setting. Both the CSCPMA and the STSCPMA are coded in Python and run on a PC with Intel Core i7 CPU, 32 GB RAM and Windows 10.

Table 1. Experimental datasets

Table 2. The default parameters of CSCPMA and STSCPMA

5.1 Efficiency Analysis

Effect of Number of Features. We compare the running time of two algorithms on Synthetic 1–4 under different number of features. From Fig. 3 we can see that the running time of both algorithms increases as the number of features varies from 10 to 15, then the running time decreases when varying from 15 to 25. The reason may be that candidate patterns are generated and tested in plenty as the number of features varies from 10 to 15, then unpromising patterns are pruned effectively when varying from 15 to 25. The running time of CSCPMA is slightly higher than that of STSCPMA because CSCPMA spends more time discovering patterns that STSCPMA cannot find.

Fig. 3.

Effect of number of features

Fig. 4.

Effect of number of instances

Fig. 5.

Effect of number of time slices

Effect of Number of Instances. We compare the running time of two algorithms on Synthetic 3 and 5–7 under different number of instances. In Fig. 4, as the number of instances gradually increases, the running time of both algorithms also increases. This is because more and denser instances lead to more star neighbors and patterns generated.

Effect of Number of Time Slices. We compare the running time of two algorithms on Synthetic 7–10 under different number of time slices. In Fig. 5, the running time of both algorithms decreases as the number of time slice increases, The reason is that sparser instances result in less patterns generated and tested.

Fig. 6.

Effect of distance threshold

Effect of Distance Threshold. We compare the running time of two algorithms on Synthetic 2,4,11 under different distance thresholds. In Fig. 6, as distance thresholds gradually increases, the running time of both algorithms also increases. The reason is that more instances satisfy the neighbor relationship when increasing distance threshold, which leads to more star neighbors and more patterns.

Fig. 7.

Effect of star participation index threshold

Effect of Star Participation Index Threshold. We compare the running time of two algorithms on Synthetic 2,4,11 under different star participation index thresholds. In Fig. 7, both algorithms show a gradual decrease in running time as the star participation index threshold increases. This is because the larger star participation index threshold will lead to the fewer patterns satisfying the threshold.

Fig. 8.

Effect of continuous sub-prevalent index threshold

Effect of Continuous Sub-prevalent Index Threshold. We analyze the running time of the CSCPMA on datasets Synthetic 2,4,11 under different continuous sub-prevalent index thresholds as only the CSCPMA has this threshold. In Fig. 8, the running time of the CSCPMA on Synthetic 2 gradually decreases as the continuous sub-prevalent index threshold increases since the pruning strategy of CSCPs work effectively. The running time of the CSCPMA on Synthetic 4 and 11 is relatively flat, the reason is that generating candidate patterns costs a lot of time, but further generating CSCPs is relatively low-cost.

5.2 Case Analysis on Real Datasets

This section will analyze the cases on two real datasets to illustrate that the CSCPMA can mine more reasonable patterns by considering the duration and the frequency of patterns in time slice set.

Table 3. Results comparison of CSCPMA and STSCPMA on Tokyo-Checkin

On the Tokyo-Checkin Dataset. Table 3 list some size-2 and size-3 patterns mined by the CSCPMA and that mined by the STSCPMA on the Tokyo-Checkin dataset. We can see that the CSCPMA mines the size-2 pattern {Movie Theater,Parking} that cannot be mined by the STSCPMA, and the pattern is reasonable in real world. Usually, there are parkings near the movie theaters for convenience of audiences. The size-3 pattern {Bar,Parking,Hotel} indicates that consumers who have drunk alcohol should not drive, and should find hotels to rest. The size-3 pattern {Mall,Coffee Shop,Barbershop} shows that coffee shops and barbershops close to malls can have the benefit from malls. Therefore, the CSCPMA can mine more reasonable patterns than the STSCPMA on Tokyo-Checkin dataset.

On the ChicagoCrime Dataset. Let us take the pattern {Robbery, Sex Offense, Battery} as an example which is mined by the CSCPMA on ChicagoCrime dataset. The pattern indicates that robbery, sexual offense, and battery occur continuously and frequently in areas with poor public security.

6 Conclusion

This paper study the spatiotemporal sub-prevalent co-location pattern to better reveal the spatiotemporal relationship of patterns. First, we consider the duration and the frequency of patterns in time slice set, and propose the continuous sub-prevalent co-location pattern. Then, we propose an efficient mining algorithm to mine the proposed pattern. Extensive experiments on synthetic datasets and real datasets verify that the proposed algorithm can efficiently mine more reasonable patterns with richer spatiotemporal relationship.