Keywords

1 Introduction

Rare-gas crystals (RGCs) combine such features of ionic and valence crystals as the closedness of atomic shells and at the same time the absence of charges in them. Thus, the main role in the formation of bonds is played by the relatively weak van der Waals forces. As an experiment showed, all RGCs under normal pressure are crystallized into the fcc structure [1]. In contrast to Ne, which retains the fcc structure up to the metallization pressure, heavier RGCs Ar, Kr and Xe, undergo structural fcc–hcp transitions under pressure. However, early theoretical studies based on pair potentials, such as the Lennard-Jones potential, unambiguously predict the hexagonal close-packed (hcp) structure for all RGCs [2, 3], resulting to the well-known “problem of RGCs structure” [4, 5]. The difficulty of this problem is due to insignificant differences in energies between fcc and hcp structures (≈ \(0.01\%\) of the binding energy) [6]. The use of more accurate potentials in calculations still leads to a preference for the hcp structure even after taking into account the three-body interaction, and only the inclusion of the zero-point energy changes the situation in favor of the fcc structure [7,8,9,10].

Not much better is obtained in ab initio calculations, based on the density functional theory, although some of them have shown the fcc structure to be energetically profitable at normal pressure [11,12,13]. This is due to the fact that the density functional theory uses a model of rigid spherical atoms and does not take into account the polarizability. Therefore, the DFT is not able to calculate with sufficient accuracy two types of dispersion forces: the long-range van der Waals interaction and the overlap effects in the short-range interaction [14, 15]. At the same time, the quantum-theoretical method provides an adequate description of both types of interaction with a sufficiently high accuracy. In the work [16, 17] for Ne and Ar, an equation of state \(P(V,T)\) was obtained using two- and three-, and four-body forces, as well as an anharmonic approximation for lattice vibrations and temperature effects in the Einstein model.

Trombach et al. [18, 19], studied the formation of a solid structure from a gas or liquid phase based on the Lennard-Jones potential. It has been shown that the extended Lennard-Jones potential chosen based on the calculations of related clusters for rare-gas dimer leads to an increase in the number of non-isomorphic clusters. The authors believe that there is still a big discrepancy between theory and experiment, despite all the advances in cluster physics.

Therefore, it is important when ab initio calculating the zero-point energy, to take into account both the many-body interaction in the short-range repulsion potential and long-range van der Waals interaction, which is the result of mutual deforming and polarizing actions of atoms.

In the work [20] a dynamic matrix was constructed in the model of deformable and polarizable atoms (Tolpygo's model see [21] and references there) taking into account the three- body forces due to the overlap of electron shells, and the deformation of the dipole type electron shells in the pair and three-body approximation. This made it possible in the present work to calculate the phonon frequencies at the desired points in the Brillouin zone and, using the Chadi-Cohen method, the zero-point energy of RGC in a wide pressure range.

2 Dynamic Matrix of Rare-Gas Crystals

The potential energy U of the lattice obtained in the Tolpygo model (see overview [21] and references there) have the form:

$$ U = \min \overline{H} = const + \sum\limits_{l} {\left\{ {\frac{{\left( {{\mathbf{P}}^{l} } \right)^{2} }}{2\alpha } + {{\varvec{\upbeta}}}^{l} \cdot {\mathbf{P}}^{l} - \frac{1}{2}\sum\limits_{{l^{\prime}}} {\frac{C}{{\left| {{\mathbf{r}}^{{ll^{\prime}}} } \right|^{6} }}} + \frac{1}{2}\sum\limits_{{l^{\prime}}} {{\text{K(}}{\mathbf{P}}^{l} {,}{\mathbf{P}}^{{l^{\prime}}} {) + }\frac{{1}}{{2}}\sum\limits_{{l^{\prime}}}^{n.n.} {U_{sr} (\left| {{\mathbf{r}}^{l} - {\mathbf{r}}^{{l^{\prime}}} } \right|)} } } \right\}} . $$
(1)

The first two terms describe the deformation of electron shells in the dipole approximation (α is the polarizability coefficient of the atom). The next term gives the van der Waals forces. K characterizes the Coulomb (in the classical sense) interaction of all dipoles \({\mathbf{P}}^{l}\) with each other. The last term in (1) is the short-range repulsion \(E_{sr}\), which contains the three-body interaction due to the deformation of atomic electron shells and their overlap [22].

The equations of lattice vibrations for the displacements of atoms \({\mathbf{u}}^{l}\) and their dipole moments \({\mathbf{P}}^{l}\) can be written as

$$ m_{e} \ddot{u}_{\alpha }^{l} = - \frac{\partial U}{{\partial u_{\alpha }^{l} }}, \, \frac{\partial U}{{\partial P_{\alpha }^{l} }} = 0, $$
(2)

where \(m_{e}\) is the mass of electron. Differentiating Eq. (2), substituting all variables \({\mathbf{p}}^{l} = e{\mathbf{u}}^{l} , \, {\mathbf{P}}^{l}\) in the form of plane waves \(\exp \left\{ {i{\mathbf{kr}} - i\omega t} \right\}\), and summing over \(l^{\prime}l^{\prime\prime\prime}\), one can obtain an equation for amplitudes \(p_{\alpha } , \, P_{\alpha }\) with the inclusion of the considered three-body interaction.

Equation (2) for determining the eigenfrequencies \(\omega_{{\lambda {\mathbf{k}}}}\), are conveniently written as two groups of equations

$$ M\omega_{{\lambda {\mathbf{k}}}}^{2} p_{\alpha } = \sum\limits_{\beta } {(A_{\alpha \beta } p_{\beta } + B_{\alpha \beta } P_{\beta } )} , $$
(3)
$$ m\omega_{{\lambda {\mathbf{k}}}}^{2} P_{\alpha } = \sum\limits_{\beta } {\left( {B_{\beta \alpha }^{*} p_{\beta } + C_{\alpha \beta } P_{\beta } } \right)} , $$
(4)

where M is the atomic mass and m is some “fictive” mass on the order of the electron shell mass, which is introduced only for the calculation convenience, because the diagonalization of a 6-by-6 matrix is technically simpler than the procedure for excluding all dipoles P from the second group of equations at m = 0, as is required by the adiabatic approximation.

Thus, it is convenient to introduce a matrix:

$$ D = \left( {\begin{array}{*{20}c} {D^{\left( 1 \right)} } & {D^{\left( 2 \right)} } \\ {D^{\left( 2 \right)} } & {D^{\left( 3 \right)} } \\ \end{array} } \right), $$
(5)

each element of which is a 3-by-3 matrix:

$$ D^{(1)} = \left( {\begin{array}{*{20}c} {A_{11} \left( {\mathbf{k}} \right)} & {A_{12} \left( {\mathbf{k}} \right)} & {A_{13} \left( {\mathbf{k}} \right)} \\ {A_{21} \left( {\mathbf{k}} \right)} & {A_{22} \left( {\mathbf{k}} \right)} & {A_{23} \left( {\mathbf{k}} \right)} \\ {A_{31} \left( {\mathbf{k}} \right)} & {A_{32} \left( {\mathbf{k}} \right)} & {A_{33} \left( {\mathbf{k}} \right)} \\ \end{array} } \right). $$
(6)

Similarly, for matrices \(D^{(2)} \left( {B_{\alpha \beta } \left( {\mathbf{k}} \right)} \right)\) and \(D^{(3)} \left( {C_{\alpha \beta } \left( {\mathbf{k}} \right)} \right)\) (see details [20]).

As an example, we present the elements of the matrix D(1), in which taken into account the three-body forces in the short-range repulsive potential due to the overlap of atomic electron shells. The diagonal matrix elements have the form:

$$ A_{11} ({\mathbf{k}}) = A_{xx} ({\mathbf{k}}) = \frac{{e^{2} }}{{a^{3} }}\left[ {\left( {H_{0} + \delta H} \right)\mu ({\mathbf{k}}) + \left( {G_{0} + \delta G} \right)\nu_{x} ({\mathbf{k}}) + F\xi ({\mathbf{k}}) + E\zeta_{x} ({\mathbf{k}}) + V_{t} \vartheta_{x} ({\mathbf{k}}) + B\chi_{xx} ({\mathbf{k}})} \right], $$
(7)

and similarly, for the other matrix elements, bearing in mind that \(1 \to x\), \(2 \to y\) and \(3 \to z\), \(4 \to x\), etc. The off-diagonal elements are

$$ \begin{gathered} A_{12} ({\mathbf{k}}) = A_{21} ({\mathbf{k}}) = A_{xy} ({\mathbf{k}}) = \frac{{e^{2} }}{{a^{3} }}\left[ {\left( {G_{0} + \delta G} \right)\tau_{xy} ({\mathbf{k}}) + B\chi_{xy} ({\mathbf{k}})} \right], \hfill \\ A_{13} ({\mathbf{k}}) = A_{31} ({\mathbf{k}}) = A_{xz} ({\mathbf{k}}) = \frac{{e^{2} }}{{a^{3} }}\left[ {\left( {G_{0} + \delta G} \right)\tau_{xz} ({\mathbf{k}}) + B\chi_{xz} ({\mathbf{k}})} \right], \hfill \\ A_{23} ({\mathbf{k}}) = A_{32} ({\mathbf{k}}) = A_{yz} ({\mathbf{k}}) = \frac{{e^{2} }}{{a^{3} }}\left[ {\left( {G_{0} + \delta G} \right)\tau_{yz} ({\mathbf{k}}) + B\chi_{yz} ({\mathbf{k}})} \right]. \hfill \\ \end{gathered} $$
(8)
$$ \begin{gathered} \mu \left( {\mathbf{k}} \right) = 3 - \frac{1}{2}\sum\limits_{\gamma \ne \delta } {\cos k_{\gamma } \cos k_{\delta } } ;\quad \nu_{\alpha } \left( {\mathbf{k}} \right) = 2 - \cos k_{\alpha } \sum\limits_{\gamma \ne \alpha } {\cos k_{\gamma } ;\quad \tau_{\alpha \beta } } \left( {\mathbf{k}} \right) = \sin k_{\alpha } \sin k_{\beta } ; \hfill \\ \xi \left( {\mathbf{k}} \right) = 3 - \sum\limits_{\gamma } {\cos 2k_{\gamma } } ;\quad \zeta_{\alpha } \left( {\mathbf{k}} \right) = 1 - \cos 2k_{\alpha } ; \, \vartheta_{\alpha } \left( {\mathbf{k}} \right) = 1 - \cos k_{\alpha + 1} \cos k_{\alpha + 2} ; \, {\mathbf{k}}\user2{ = }a\user2{K = }\pi {\varvec{q}}\user2{.} \hfill \\ \end{gathered} $$

Here, k is the dimensionless wave vector; \(H_{0} (a\sqrt 2 )\) and \(G_{0} (a\sqrt 2 )\) are, respectively, the first and second derivatives of the short-range repulsion pair potential for the equilibrium distances of the first neighbors; by analogy, for the second neighbors \(F = H_{0} (2a)\) and \(E = G_{0} (2a)\); B determines the van der Waals interaction. Parameters \(\delta G, \, \delta H\) and \(V_{t}\) describe the three-body short-range forces due to the electron shell overlap of atoms (see [21] and references therein). \(\chi_{\alpha \beta } ({\mathbf{k}})\) are the functions of the wave vector k originated from the van der Waals forces. They do not depend on specific parameters of crystal and are identical for all materials with the same lattice type. The exactly calculated sums of \(\chi_{\alpha \beta } ({\mathbf{k}})\) for two and ten mean-value points were presented in [23].

Note that elements of the matrix \(D^{\left( 2 \right)}\) contain the deformation of the electron shell for dipole-type atoms within the pair and three-body approximations. Thus, diagonalization of the dynamic matrix D will give us phonon frequencies at any point in the Brillouin zone, for example at the mean-value points of the Chadi–Kohen method [24].

3 Phonon Frequencies at the Mean-Value Points

All parameters of the short-range action, both pair and three-body, are calculated exactly [21]. When determining the van der Waals constant, one should take into account the equilibrium condition:

$$ H_{0} + \delta H + 2F - 2R_{t} = 0.30112B, $$
(9)

where

\(R_{t} = - \frac{{a^{{}} }}{{6e^{2} }}\frac{{dW_{3} (a)}}{da}\); \(W_{3} (a) = - 24S^{2} (a\sqrt 2 )f(\frac{\sqrt 6 }{2}a)\); S is the overlapping integral.

The paper [22] presents the values of the parameters of pair short-range action G0, H0, E, F, three-body interaction \(\delta H, \, \delta G, \, V_{t}\), dipole deformation, and van der Waals parameter B under various compressions \(u = \Delta V/V_{0}\), \(\Delta V = V_{0} - V(p)\) (where \(V_{0}\) is the volume at \(p = 0\)) for the Ne – Xe series.

The phonon frequencies \(\hbar \omega_{\lambda } ({\mathbf{k}}_{i} )\) calculated within the models MT0 (the three-body interaction due to the electron shell overlapping is taken into account and the deformation of atomic electron shells is disregarded) and MT2 (the three-body forces due to the electron shell overlapping and electron shell deformation for dipole-type atoms within the pair and three-body approximations are taken into account) for Ar at compression ratios in the range from 0 to 0.71 are listed in the Table 1.

Table 1 Phonon frequencies \(\hbar \omega_{{\lambda {\mathbf{k}}}}\) [meV] in models MT0 and MT2 and relative contribution of the effects of electron shell deformation within the pair and three-body approximations γ1 at different degrees of compression u for Ar at the ten mean-value points of the Chadi-Kohen method
Full size table
$$ \gamma_{1} = \left[ {\left| {\omega (MT_{0} ) - \omega (MT_{2} )} \right|/\omega (MT_{0} )} \right] \cdot 100\% $$

As can be seen from the Table 1, the phonon frequencies are quite sensitive to the addition of the contribution of electron shell deformation in pair and three-body approximations γ1. It is varied, depending on the point in the Brillouin zone, from 0.06% to 58.38% at compression \(u = 0.71\); however, its average value is 23.2%. Similar tendency is observed for the other RGCs. The average value of γ1 for Ne is 17% at u = 0.76; 16.50% at \(u = 0.68\) for Kr and 11.53% at \(u = 0.6\) for Xe. The compression limitations ui = 0.76; 0.71; 0.68; 0.6 are caused by the absolute instability of the fcc lattice for Ne, Ar, Kr, and Xe, respectively [25].

4 Zero-Point Energy of Compressed Rare-gas Crystals

The binding energy of the crystals in the harmonic approximation are described by the standard formulas:

$$ E_{coh} = E_{zp} + E^{*} = \frac{{N_{A} \Omega }}{{\left( {2\pi } \right)^{3} }}\sum\limits_{\lambda } {\int {d^{3} k\hbar \omega_{\lambda } \left( {\varvec{k}} \right)\left[ {\frac{1}{2} + n_{\lambda } \left( {\mathbf{k}} \right)} \right]} } .;n_{\lambda } ({\mathbf{k}}) = \left[ {\exp \left( {\hbar \omega_{\lambda } ({\mathbf{k}})/k_{B} T} \right) - 1} \right]^{ - 1} $$
(10)

Here, \(E_{zp}\) is the zero-point energy (it corresponds to the term of 1/2 in parentheses in (10)), NA is the Avogadro number, \(\Omega = 2a^{3}\) is the RGC unit-cell volume in the fcc phase, a is the lattice parameter equal to a half of the cube edge, and kB is the Boltzmann constant.

The integrals over the Brillouin zone are calculated with the use of the Chadi–Cohen method [24]. This the method consists in replacing the integral over the Brillouin zone by the sum of the values of the integrand at special points (the mean-value points) determined by group-theoretical methods [26].

In work [24] proposed the method for generating these points with the use of two mean-value points k1 and k2 in order to determine f(k) for the crystal:

$$ f({\mathbf{k}}) = \frac{1}{4}\left[ {3f({\mathbf{k}}_{1} ) + f({\mathbf{k}}_{2} )} \right],{\mathbf{k}}_{1} = \left[ {\frac{3}{4};\frac{1}{4};\frac{1}{4}} \right],{\mathbf{k}}_{2} = \left[ {\frac{1}{4};\frac{1}{4};\frac{1}{4}} \right] $$
(11)

Then, the zero-point energy calculated according to the two-point scheme (11) of the Chadi Cohen method has the form:

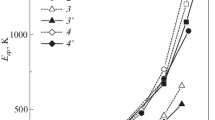
$$ E_{zp} = \frac{1}{2}\left[ {\frac{3}{4}\sum\limits_{\lambda } {\hbar \omega_{\lambda } ({\mathbf{k}}_{1} )} + \frac{1}{4}\sum\limits_{\lambda } {\hbar \omega_{\lambda } ({\mathbf{k}}_{2} )} } \right]. $$
(12)

Figure 1 shows the dependences of the energy of zero-point energy Ezp on the compression ratio of crystals from the Ne – Xe series according to calculations in the MT0 model without regard for the electron shell deformation and the MT2 model with due regard for the electron shell deformation for dipole-type atoms within the pair and three-body approximations.

It can be seen that the largest difference between the models is observed for crystalline Ar and manifests itself at \(u > 0.5\) for Ne, Ar, and Kr. For Xe, it is insignificant for the entire compression range.

Table 2 presents the calculation of the zero-point energy according to the two-point Chadi-Cohen scheme in models M3 (pair interaction in the short-range repulsion potential without taking into account the deformation of the atomic electron shells), M3a (pair interaction taking into account the deformation of the atomic electron shells within the pair approximation), MT0 and MT2. As can be seen with increasing pressure (compression), the contribution of the deformation of the electron shells of dipole type atoms within the pair and three-body approximation (γ1) to the zero-point energy increases. Comparisons of the calculation results in the models M3, MT0 (γ2) and M3a, MT2 (γ3) shows that the relative contributions from three-body forces due to the overlap of the electron shells (γ2) are small and increase slightly with an increase in pressure only for Kr and Xe. The effect of both types of the three-body interaction on Ezp is more significantly γ3 > γ2 for the entire compression interval. The behavior of γi for the zero-point energy Ezp of compressed RGCs is close to that of the average γi, values obtained in calculations of the phonon frequency energy.

Fig. 1
figure 1

Dependence of the zero-point energy Ezp on compression u for (1) Ne, (2) Ar, (3) Kr, and (4) Xe; Ezp values are calculated in (1 – 4) model MT0 and (1’ – 4’) model MT2

Full size image

Unfortunately, we know experimental data on the zero-point energy Ezp for Ne, Ar and Kr only at p = 0 [27, 28]. In our work, the zero-point energy Ezp in model MT2 for Ne is 79.185 K. The experimental zero-point energy for Ne is Ezp = 78.5 [28]. The error in our calculations as compared to the experimental value is approximately equal to 1.4%.

The experimental zero-point energy is Ezp = 86.1 ± 2.5 K for Ar [27] (the discrepancy is γ = 11.95%) and 67.4 ± 3 K for Kr [27] (the discrepancy is γ = 7.77%). The worst consistency between our and experimental Ezp values is for Ar; although, it should be taken into account that the experimental error is 3% for Ar and 4% for Kr.

The zero-point energy was calculated in [9] for the entire Ne – Xe series in the Debye model from the formula: \((9/8)k_{B} T_{Debye}\) [29] (the Debye temperature was taken from [30]) at p = 0. The discrepancy between the calculated and experimental values was obtained for Ne (Ezp = 267 μHartree (μH) = 84.312 К (1 H = 2 Ry = 31.5777 × 104 K)); Ar (Ezp = 328 μH = 103.6 К) and Kr (Ezp = 257 μH = 81.16 К). It was equal to 7%, 20%, 20%, respectively, that is, it was in much worse agreement with the experiment as compared to our values.

Note that our best the zero-point energy Ezp value were obtained in model MT2, which take into account the three-body interaction and deformation of dipole-type atomic electron shells within the pair and three-body approximations.

Table 2 Zero-point energy Ezp [K], calculated according to the two-point Chadi – Kohen scheme in models M3, M3a, MT0, and MT2 and relative contributions of the three-body interaction and effects of electron shell deformation γi [%] at different degrees of compression for Ne – Xe series
Full size table

5 Conclusions

Schwerdtfeger et al. [16], using the quantum-theoretical method, conducted studies of the influence of the many-body forces, the energy of zero-point vibration and anharmonism on the equation of state of crystalline Ar. The dynamic part was calculated in the approximation of Debye and Einstein. The quantitative analysis showed that pair forces make the greatest influence, regardless of pressure. It was also found that it is enough to take into account the contribution of three-body forces at pressures up to 20 GPa to obtain good agreement with the experiment. At the same time, at high pressure, the situation is different. A significant discrepancy between theoretical and experimental data is observed at a pressure of 20–100 GPa, which may indicate the need to include four-, five- and more body forces. This contradicts the authors’ previous results obtained in the calculation of the equations of state for Ne [17], where for good agreement with the experimental data, it is sufficient to confine oneself to the consideration of pair and three-body forces.

Our study of phonon frequencies for Ar at ten mean-value points showed that the contribution of three-body forces due to the electron shells overlap was small against the background of pair interaction, and the effects of electron shell deformations within the pair and three-body approximation (\(\gamma_{1}\)) differ for different main-value points. As can be seen from Table. 1 the contribution for electron shell deformations is varied from 0% to 0.86% under compression u = p = 0, and from 0.06% to 58.4% at u = 0.71. Note that the average value of the contribution increases with increase in pressure from 0.44% to 23.9%. Since the zero-point energy is an integral function of phonon frequencies, the contribution of the electron shell deformations within the pair and three-body approximation is close to the average contribution to phonon frequencies.

In conclusion, it is worth noting that the influence of electron shells deformation on the zero-point vibrations energy is not as pronounced as, for example, when softening phonon frequencies at the “critical” points of the Brillouin zone [25]. However, taking into account the deformation of electron shells is fundamentally important for a correct description of the van der Waals attraction potential.