Keywords

1 Introduction

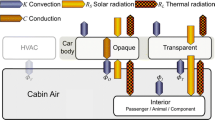
One of the urgent tasks of thermal comfort and maintaining safe operating conditions for transport (HVAC) is the task of maintaining comfortable values of temperature, speed and air humidity in the area of machine operator (see Fig. 1).

An equally important issue with HVAC relates to driver visibility and window fogging. This phenomenon is commonly referred to as the “dew point”, and it consists in the steam reaching a state of saturation on the surface, in particular the window, due to the temperature difference. Water vapor can enter the cabin both from the ventilation system from the ambient air and from the breathing of passengers.

To unambiguously determine the “dew point”, it is necessary to determine the amount of water vapor in the air, the temperature and pressure at the desired points.

The factors that provide a comfortable microclimate and the theoretical foundations for modeling the microclimate in cabins, based on the balance equations of heat flows, are given in [1].

To obtain the fields of these quantities, an algorithm, based on the numerical solution of the Navier–Stokes equations and the energy equation together with the convection-diffusion equations [2,3,4,5,6,7,8,9,10, 21,22,23,24], is proposed. For the numerical implementation of the model, the ANSYS Fluent computer fluid dynamics complex is used.

In works [11,12,13,14,15,16,17,18,19], the results of CFD analysis of thermal and hydrodynamic characteristics for various vehicles are presented, optimization issues for various configurations and cabin geometries are considered.

When modeling, the initial data are, in particular, the proportions of wet steam and air, or the relative humidity of the air in the deflectors of the climate system. The problem is solved in a non-stationary formulation, and the fields of pressure, velocities, temperature, density and relative humidity inside the cabin are calculated.

Fig. 1
figure 1

Harvester cabin: (a) outside, (b) inside

Full size image

1.1 Research Purpose

A numerical model for modeling the thermal state of the vehicle cabin is studied, taking into account the humidity field.

1.2 Research Scope

In this work, the following tasks are investigated:

  1. (i)

    a mathematical model for modeling the fields of velocity, density, pressure, temperature and humidity based on the Navier–Stokes equations, energy and diffusion equations was built; the cabin was located in an external aerodynamic flow to simulate the heat exchange between the cabin and the environment;

  2. (ii)

    the averaged RANS equations are solved numerically using turbulence models;

  3. (iii)

    the non-stationary problem of changing the humidity inside the cabin during air injection was studied;

  4. (iv)

    the temperature, velocity, and humidity fields of the stationary time-stabilized problem of blowing air into the cabin are studied.

2 Research Method

2.1 Continuous Formulation of the Problem

To describe the behavior of a compressible viscous gaseous medium, the Navier–Stokes Eqs. (1) are used together with the continuity Eq. (2):

$$ \frac{{\partial {{\varvec{u}}}}}{\partial t} + \left( {{{\varvec{u}}} \cdot \nabla } \right){{\varvec{u}}} = {{\varvec{X}}} - \frac{1}{\rho }\nabla p + \eta \cdot {{\varvec{u}}} + \frac{1}{3}\eta \nabla \nabla \cdot {{\varvec{u}}}, $$
(1)
$$ \frac{\partial \rho }{{\partial t}} + \nabla \cdot \left( {\rho {{\varvec{u}}}} \right) = 0, $$
(2)

Here \({{\varvec{u}}} = {{\varvec{u}}}\left( {x,y,z,t} \right)\) is the medium velocity in Euler variables; \(p = p\left( {x,y,z,t} \right)\) is the pressure; \(\rho = \rho \left( {x,y,z,t} \right)\) is the density; \(\eta = \mu /\rho\), where μ и η are the dynamic and kinematic viscosity, respectively, \(\mu\) is the considered permanent; \({{\varvec{X}}} = {{\varvec{X}}}\left( {x,y,z,t} \right) \) are the volumetric forces.

To take into account the mass amount of water vapor in the air, energy Eq. (3) are used to take into account temperature, taking into account diffusion and mass transfer Eqs. (4) and (5) [2,3,4,5,6,7,8,9,10]:

$$ \frac{\partial T}{{\partial t}} + {{\varvec{u}}}\nabla T = \frac{\lambda }{_\rho \rho } \cdot T - \nabla \cdot \mathop \sum \limits_{i = 1}^n {{\varvec{J}}}_i + \phi , $$
(3)
$$ \frac{\partial \rho Y_i }{{\partial t}} + \nabla \cdot \left( {\rho {{\varvec{u}}}Y_i } \right) = \nabla \cdot {{\varvec{J}}}_i , i = 1..N - 1, $$
(4)
$$ \sum_{i = 1}^n {Y_i \, = 1} . $$
(5)

Here \(T = T\left( {x,y,z,t} \right)\) is the temperature, \(\lambda\) and \(c_\rho\) are the thermal conductivity and specific heat assumed constant, \(\phi\) is the internal heat source, \(Y_i\) is the local mass fraction of i-th substance, \({{\varvec{J}}}_i\) is the diffuse flow of i-th substance, which arises due to the gradient of concentrations, temperature and pressure; for the turbulent case, it is written as follows:

$$ {{\varvec{J}}}_i = \left( {\rho D_{i,m} + \frac{\mu_t }{{Sc_t }}} \right)\nabla Y_i + D_{i,T} \frac{\nabla T}{T} + D_{i,p} \frac{\nabla p}{p}. $$
(6)

Here \(Sc_t \) is a turbulent Schmidt number, \(\mu_t \) is the turbulent viscosity, \(D_{i,m} \) are the mass diffusion coefficients, \(D_{i,T} \) are the thermal diffusion coefficients (thermal diffusion coefficients), \(D_{i,p} \) are the barotropic diffusion coefficients i-th substance. The last barotropic term in (6) is taken into account in the presence of a large pressure gradient.

The diffusion coefficients characterize the diffusion rate, equal to the amount of a substance, passing per unit time through a section of a unit area, caused by a gradient of concentration, temperature and pressure, respectively.

To close the system of equations of hydrodynamics, the Mendeleev-Clapeyron equation of state for an ideal gas (7) is used, which relates the variable pressure and density:

$$ p = \frac{\rho TR}{M}, $$
(7)

here \(R\) is a universal gas constant, \(M\) is the molar mass.

2.2 Boundary Conditions

As the boundary conditions on the boundary between the domain and the rigid body \({\Omega }\), the no-slip conditions for the medium are given as

$$ {{\varvec{u}}}_n |_{\Omega } = 0, {{\varvec{u}}}_\tau |_{\Omega } = 0, $$
(8)

here \({{\varvec{u}}}_n {\text{and}}\,{{\varvec{u}}}_\tau\)

are the normal and tangential components of the velocity vector \({{\varvec{u}}}\).

Velocity values (profiles) are set at the input as

$$ {{\varvec{u}}} = {{\varvec{u}}}^* . $$
(9)

Pressure values are set at the output as

$$ p = p^* $$
(10)

In the numerical implementation, the equations take into account the pressure relative to the reference atmospheric pressure.

Since the moment equation contains second derivatives of velocities, it is necessary to set additional boundary conditions. Typically, such conditions are introduced at the output as the value of certain velocities or derivatives of velocities equal to zero, which means the absence of velocities in some directions and the uniformity of velocities at the output of their area.

For the equation of energy and diffusion at the boundary, at the input and output of \({\Omega }\), the values of temperatures, heat fluxes or convective heat transfer (11) are set as

$$ T|_{\Omega } = T^* , - \lambda \frac{\partial T}{{\partial n}}|_{\Omega } = q^* = - \alpha \left( {T - T_{out} } \right). $$
(11)

For diffusion, the boundary conditions are set similarly to thermal boundary conditions (11) in the form of values of concentrations, fluxes, or convective exchange at the boundaries:

$$ Y_i |_\Omega = Y_i^* , - \frac{\partial Y_i }{{\partial n}}|_\Omega = {\bf{J}}_i^* . $$
(12)

For the case of unsteady motion of the medium at the zero moment of time, the initial values of all fields are set.

Thus, the system of Eqs. (1)−(7) together with the boundary and initial conditions (8)–(12) form a closed boundary-value problem of differential equations for velocities \({{\varvec{u}}}\), pressure \(p\), temperature \(T\) and concentrations \(Y_i\).

3 Results and Discussion

3.1 Numerical Analysis

For the numerical solution of the equations of hydrodynamics, the fields are averaged according to Reynolds:

$$ f = \overline{f} + f^{\prime}, $$
(13)

here

$$ \overline{f} = \frac{1}{T}\smallint_{t - T/2}^{t + T/2} f\left( \tau \right)d\tau $$

and \(f^{\prime}\) is the ripple component.

After substituting the averaged fields into Eqs. (1)−(6) and re-averaging Eqs. (1)−(6), systems of differential equations are obtained in respect to the averaged fields, as well as in respect to additional new turbulence parameters (RANS). The RANS equations are solved numerically using turbulence models.

To date, many turbulence models are known, each of which in certain cases shows sufficient accuracy [25,26,27,28,29]. The most universal are the k − ε and k − ω turbulence models [29], where the turbulence kinetic energy k and the kinetic energy dissipation rate ε for the first case, as well as the turbulence kinetic energy k and the specific kinetic energy dissipation rate ω in the second case are given as additional unknown.

Further, all characteristics are considered averaged, the bar from above is deleted.

Fig. 2
figure 2

General scheme: (a) circuit inputs/outputs, (b) mesh of finite volumes

Full size image

In this paper, the boundary-value problem is modeled numerically by the finite volume method in the ANSYS Fluent software product. The k − ω turbulence model is used as the most universal one [20, 25, 30,31,32].

Schematically, we shows in Fig. 2a, a rectangular cabin of technological transport in a wind tunnel. Inside the cabin there is a source through which air enters at a given speed, temperature and humidity. The outputs are set to zero relative pressure. For clarity, all results are given for the average section of the cabin for a plane formulation of the problem.

Figure 2b shows a finite volume grid of 32,518 cells with six near-wall layers to account for the gradient of boundary effects.

The minimum cell area is 1.1 × 10−3 m2, the maximum is 5.5 × 10−3 m2.

The grid orthogonality parameter is 0.6, which is quite acceptable for such problems [25].

3.2 Task Parameters

The cabin wall (top, right) is a multilayer structure with the following thermal conductivity coefficients, presented in Table 1.

Table 1 Wall parameters
Full size table

The thermal conductivity coefficient for the walls is calculated equal to 0.33 W/(m·K), at a wall thickness of 0.0312 m from data of Table 1 and formulae (14), (15):

$$ R = \sum \frac{\delta_i }{{\lambda_i }}, $$
(14)
$$ \alpha = \frac{1}{R} $$
(15)

where R is the coefficient of thermal resistance, \(\delta_i {\text{and}} \lambda_i \) are the thickness and thermal conductivity of the i-th wall, \(\alpha\) is the thermal conductivity coefficient for the walls.

The left wall from laminated glass has the thermal conductivity coefficient of 0.96 W/(m·K).

The bottom wall (floor) is thermally insulated.

Table 2 shows the values of the boundary conditions and air parameters.

The decrease in the mass fraction of water vapor in cold air due to condensation on the air conditioner evaporator, as well as the driver's breathing, were not taken into account.

Table 2 Boundary conditions and environment parameters
Full size table

Relative humidity is determined by the formula:

$$ \varphi = \frac{{p_{H_2 O} }}{{p_{H_2 O }^* }}100\% , $$
(16)

here \(p_{{\text{H}}2{\text{O}}}\) is the partial pressure of water vapor, \(p_{{\text{H}}2{\text{O}} }^*\) is the equilibrium saturation vapor pressure.

The equilibrium pressure of saturated vapor can be represented by the Arden Buck formula for positive and negative temperatures, respectively [33]:

$$ p_{H2O }^* = 6.1121e^{\left[ {\frac{{\left( {18.678 - \frac{T}{234.5}} \right) \cdot T}}{257.14 + T}} \right]} 100, $$
(17)
$$ p_{H2O }^* = 6.1115e^{\left[ {\frac{{\left( {23.036 - \frac{T}{333.7}} \right) \cdot T}}{279.82 + T}} \right]} 100, $$
(18)

here \(T\) is the temperature in Celsius degrees.

Using the Mendeleev–Clapeyron law (7) for a fixed temperature, relative humidity can be expressed in terms of mass fractions of water vapor. Thus, for the mass fractions, shown in Table 2 and temperatures of 30 ℃ and 14 ℃, the relative humidity is equal to 34.7% and 92.2%, respectively.

3.3 Numerical Results

At the first stage, a non-stationary problem was solved. The initial temperature of the outer area and inside the cabin was set to 30 ℃, the mass fraction of water vapor was set to 0.0091, which corresponded to a relative humidity of 34.7%. The field stabilization time over time was 70 s (see Fig. 3). The average temperature in the cabin after 70 s was equal to 15.8 ℃. The average humidity in the cabin was 83.2% (see Fig. 4).

Fig. 3
figure 3

Average temperature

Full size image
Fig. 4
figure 4

Average relative humidity

Full size image

Further, all processes can be considered as stabilized in time, and a stationary formulation can be used. Figures 5, 6, 7, 8 and 9 show plots of the fields of velocities, pressures, temperatures, densities and air humidity.

Fig. 5
figure 5

(a) Relative pressure, Pa; (b) air density, kg/m3

Full size image
Fig. 6
figure 6

Velocity field, m/s: (a) in all areas; (b) in cabin

Full size image
Fig. 7
figure 7

Vector velocity field, m/s: (a) in all areas; (b) in cabin

Full size image
Fig. 8
figure 8

Temperature, ℃: (a) in cabin; (b) in all areas

Full size image
Fig. 9
figure 9

Relative humidity ℃: (a) in all areas; (b) in the cabin

Full size image

The velocity and temperature fields inside the cabin turn out were substantially inhomogeneous. The minimum air temperature in front of the driver was 14 ℃, the maximum above the walls was 29.2 ℃. The relative humidity values ​​in the cabin were in the range of 39.2−92.2%. Moreover, there was an air stagnation in the upper right part of cabin.

The flow and direction of the air flow, and therefore the temperature and humidity, can be significantly affected by the interior equipment in the cabin. Numerical simulation in this case makes it possible to choose the optimal combinations of the direction of the air entering the compartment of driver (deflector configuration), the number and location of deflectors, the speed and temperature of the air flow.

4 Conclusions

In the course of the study, numerical and analytical modeling of the thermal state and humidity inside the cabin was carried out, taking into account external airflow and internal ventilation. To obtain a numerical solution, the Navier – Stokes equations are used together with the diffusion equation to model humidity.

This approach can be applied to simulate the thermal state of cabins of any complexity and high air flow rates, as well as various configurations of climate equipment inside the cabin. The presented model also allows one to simulate the humidity inside the cabin, including effectively determining the formation of a “dew point” on the inner surface of the vehicle window and provides opportunities to minimize this phenomenon by controlling the parameters of temperature, direction, speed and humidity of the incoming air from the transport climate system.