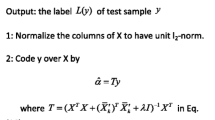Keywords

1 Introduction

Imbalanced classification has become an important research direction in pattern recognition due to the prevalence of imbalanced datasets in the real world. Traditional classifiers generally achieve good classification results on balanced datasets but cannot work well on imbalanced datasets [14, 15, 18, 19]. Imbalanced class distribution makes traditional classifiers more inclined to the majority classes, which results in poor overall classification accuracy [8]. In practice, the minority classes usually contain more important and valuable information than the majority classes. Once they are misjudged, there may be serious consequences. For example, judging an intrusion as a normal behavior may cause a major network security incident; misdiagnosing a cancer patient as a normal person will delay the best treatment time and threaten the patient’s life. Therefore, it is necessary and urgent to improve the classification accuracy of the minority classes.

At present, there are two main aspects to improve the imbalanced classification methods [4, 12]. One is from the data-level, and the other is from the algorithm-level. The former is mainly to improve the classification performance by balancing the class distribution [1, 11, 13]. Random under-sampling (RUS) and random oversampling (ROS) [3, 9] are two commonly used sampling techniques. RUS randomly reduces the majority samples to the same number size as the minority samples, but it may lose potential information. To overcome this defect, EasyEnsemble [20, 24] introduced data cleaning scheme to improve RUS. It randomly selects several subsets from the samples of the majority classes and combines them with the data of the minority classes to train and generate multiple base classifiers, which improves the learning performance. ROS is to copy the randomly selected minority class samples and add the generated selection set to the minority classes to obtain new minority class instances. Nevertheless, it may lead to overfitting. To address the overfitting problem, the authors in [6] proposed a synthetic minority over-sampling technique (SMOTE) by using interpolation theory. Afterwards, many variants of SMOTE such as adaptive synthetic sampling (ADASYN) [10], majority weighted minority oversampling technique (MWMOTE) [1], SMOTEENN [2] were provided to obtain more effective minority class instances. However, both oversampling and undersampling would destroy the relationship between the original data so that the final recognition accuracy cannot be significantly improved.

The algorithm-level is to improve the classification accuracy by enhancing the traditional classification approaches [5, 23, 25]. The core idea of this type is to give different weights to samples of different classes to improve the classification performance of the minority classes. Among them, the spare supervised representation-based classifier (SSRC) [21] shows excellent advantages. It introduces label information and class weights into SRC to improve the classification accuracy. But the extremely high computational complexity limits its further development and application. Inspired by this, in this paper we choose the efficient and effective CCRC [26] as the base model for imbalanced classification. We incorporate a class weight learning algorithm into CCRC according to the representation ability of each class of training samples. The algorithm adaptively obtains the weight of each class and can assign greater weights to the minority classes, so that the final classification results are more fair to the minority classes. The proposed model can be solved efficiently with a closed-form solution. Experimental results on authoritative public imbalanced datasets show that our method outperforms other commonly used imbalanced classification algorithms.

The remainder of this paper is organized as follows. Section 2 briefly introduces the related work. The proposed imbalanced classification method is described in Sect. 3. Experimental results are shown in Sect. 4. Finally, Sect. 5 draws the conclusion.

2 Related Work

This section introduces the nearest subspace classification (NSC) [19], collaborative representation based classification (CRC) [22], and CCRC [26] algorithms that are closely related to our method. First, the symbols used in the paper are given. \(\text {D}=[D_{1},...D_{n},...D_{N}]\) represents the entire training sample set, where \(D_{n}\in \mathbb {R}^{d\times { M_{n}}}\) represents the training sample set of class n. \(M_{n}\) is the number of samples in \(D_{n}\), and d is the feature dimension of each sample. \(M=M_{1}+M_{2}+...M_{N}\) represents the number of all training samples. \(x\in \mathbb {R}^{d}\) represents a test sample. \(c=[c_{1};...c_{n};...c_{N}]\) is the coefficient vector of x over D, \(c^{*}=[c_{1}^*;...c_{n}^*;...c_{N}^*]\) is the optimal coefficient vector of x over D. \(c_{n}\) is the coefficient vector of x over \(D_{n}\), \(c_{n}^*\) is the optimal vector of x over \(D_{n}\). I is the identity matrix. \(\gamma \) and \(\alpha \) represent the regularization parameters. \(\beta _{n}\) represents the weight of class n.

2.1 NSC

NSC calculates the distance between the test sample x and each class of the training set and classifies x into the class of its nearest subspace. The specific model is as follows

$$\begin{aligned} c_{n}^*=\arg \min _{c_n}\Vert x-D_{n}c_{n}\Vert _2^2 . \end{aligned}$$
(1)

It has a closed-form solution

$$\begin{aligned} c_{n}^*=(D_{n}^{T}D_{n})^{-1}D_{n}^{T}x. \end{aligned}$$
(2)

According to the minimum reconstruction error criterion, the label of x is predicted as

$$\begin{aligned} \text {label}(x)=\arg \min _{n}\Vert x-D_{n}c_{n}^{*}\Vert _{2} . \end{aligned}$$
(3)

2.2 CRC

NSC uses each class of training samples to represent the test samples individually. However, CRC takes all the training samples as a whole to collaboratively represent the test samples. Given a test sample x, CRC solves the minimum problem by introducing \(\ell _2\)-norm regularization

$$\begin{aligned} c^*=\arg \min _c\Vert x-Dc\Vert _2^2+\gamma \Vert c\Vert _2^2. \end{aligned}$$
(4)

The above equation also has a closed-form solution

$$\begin{aligned} c^*=(D^{T}D+\gamma I)^{-1}D^{T}x. \end{aligned}$$
(5)

With the optimal coefficient vector, the classification result of x is obtained

$$\begin{aligned} \text {label}(x)=\arg \min _{n}\Vert x-D_{n}c_{n}^{*}\Vert _{2}. \end{aligned}$$
(6)

2.3 CCRC

CCRC introduces a competition mechanism into the CRC model, and its model is expressed as follows

$$\begin{aligned} c^*=\arg \min _c\Vert x-Dc\Vert _2^2+\gamma \Vert c\Vert _2^2+\alpha \sum _{n=1}^{N}\Vert x-D_{n}c_{n}\Vert _2^2, \end{aligned}$$
(7)

where \(\sum _{n=1}^{N}\Vert x-D_{n}c_{n}\Vert _2^2\) reflects the competitiveness of each class. \(\alpha \) is the regularization parameter that balances competitiveness and collaborativeness. The model can also be solved analytically

$$\begin{aligned} c^*=(1+\alpha )(D^{T}D+\gamma I+\alpha G)^{-1}D^{T}x, \end{aligned}$$
(8)

where G is defined as

$$\begin{aligned} G=\left[ \begin{matrix}{} D_1^TD_1 &{} \cdots &{} 0\\ \vdots &{} \ddots &{} \vdots \\ 0 &{} \cdots &{} D_n^TD_n \\ \end{matrix} \right] . \end{aligned}$$
(9)

After obtaining the optimal coefficient vector \(c^*\), CCRC classifies the test samples x according to the same classification criterion as CRC. Here, we will not repeat it.

3 Proposed Method

This section describes the weighted competitive-collaborative representation based classifier (WCCRC) model in detail. First, a class weight learning method is introduced into the CCRC model to give different weights to different classes. Next, the proposed model is solved with a closed-form solution. Finally, the classification criterion is given.

3.1 WCCRC Model

CCRC introduces a competition mechanism between each class of samples. Assuming that the true label of a given test sample x is k, CCRC desires the intra-class loss \(\Vert x-D_nc_n\Vert _2^2\) to be as small as possible and the inter-class loss \(\{\Vert x-D_nc_n\Vert _2^2\}_{n=1,n\ne k}^{N}\) to be as large as possible. Since the actual label is unknown, the model minimizes the sum of all losses \(\sum _{n=1}^{N}\Vert x-D_nc_n\Vert _2^2\). However, it does not consider class distribution information. When handling imbalanced classification tasks, CCRC generally makes the representation ability of the majority classes far more than the minority classes, resulting in the final classification results leaning towards the majority classes. Especially for severely imbalanced datasets, the minority classes usually have an extremely low representation for test samples. This will make their reconstruction error larger than the majority classes, which is not conducive to the final classification. In this section, we assign different weights to different classes in CCRC based on NSC. Our objective function is expressed as

$$\begin{aligned} c^*=\arg \min _c\Vert x-Dc\Vert _2^2+\gamma \Vert c\Vert _2^2+\alpha \sum _{n=1}^{N}\beta _{n}\Vert x-D_{n}c_{n}\Vert _2^2. \end{aligned}$$
(10)

It is called weighted competitive-collaborative representation based classifier (WCCRC) model.

3.2 Class Weight Learning Based on NSC

We use the reconstruction error of each class in the NSC model to learn each class weight. According to Sect. 2.1, the optimal coefficient vector of x over \(D_{n}\) is

$$\begin{aligned} c_{n}^*=(D_{n}^{T}D_{n})^{-1}D_{n}^{T}x. \end{aligned}$$
(11)

The reconstruction error of this class to x is

$$\begin{aligned} r_{n}=\Vert x-D_{n}c_{n}^*\Vert _{2}. \end{aligned}$$
(12)

We define the maximum reconstruction error as

$$\begin{aligned} r_{max}=\max \{r_n\}. \end{aligned}$$
(13)

Obviously, the larger the \(r_n\), the weaker the representation ability of \(D_n\) to x. The less likely it is that x belongs to the nth class. On the basis of this fact, the weight of the nth class is defined as

$$\begin{aligned} \beta _n=\exp (\frac{r_{n}-r_{max}}{\delta }), \end{aligned}$$
(14)

where the scaling parameter \(\delta >0\) is to control the class weight. Taking binary-classification as an example, we can show this method can indeed give greater weights to the minority classes. Assuming that the first class is the minority class, it has a weak representation of the test sample. The reconstruction error \(r_1>r_2\), then \(r_{max}=r_1\). Thus, \(\beta _1=\exp (\frac{r_{1}-r_{1}}{\delta })=1\) and \(\beta _2=\exp (\frac{r_{2}-r_{1}}{\delta })<1\). We get that the NSC-based class weight learning algorithm can give the minority classes greater weights for binary-classification. For multi-classification, its weighting analysis is more complicated than binary-classification. We will use experimental results in Sect. 4 to show the effectiveness of this class weight update mechanism. Algorithm 1 describes the specific steps of class weight learning.

3.3 Optimization Solution and Classification Criterion

To solve the minimization problem (10) in the WCCRC model, we first give a new matrix \(\tilde{D}_n=\left[ 0,\ldots ,0,{D}_n,0,\ldots ,0\right] \) which keeps the columns of the nth class in D and sets the other columns to zero. The theorem below can guarantee WCCRC has a closed-form solution.

Theorem 1

Given each class weight \(\beta _n\), the WCCRC model is solved as

$$\begin{aligned} c^*=(D^TD+\alpha \sum _{n=1}^{N}\beta _n\tilde{D}_n^T\tilde{D}_n+\gamma I)^{-1}(D+\alpha \sum _{n=1}^{N}\beta _n\tilde{D}_n)^Tx. \end{aligned}$$
(15)

Proof

For ease of computation, the objective function in problem (10) can be written as

$$\begin{aligned} \vartheta =\Vert x-Dc\Vert _2^2+\gamma \Vert c\Vert _2^2+\alpha \sum _{n=1}^{N}\beta _{n}\Vert x-\tilde{D}_{n}c\Vert _2^2. \end{aligned}$$
(16)

Then take the derivation of \(\vartheta \) with respect to c to be zero

$$\begin{aligned} \frac{\partial \vartheta }{\partial c}= & {} -2D^T(x-Dc)+2\gamma c+\alpha \sum _{n=1}^{N}\beta _n[-2\tilde{D}_{n}^{T}(x-\tilde{D}_nc)] \\= & {} 0. \end{aligned}$$

So the closed-form solution \(c^*\) can be easily obtained as

$$\begin{aligned} c^*=(D^TD+\alpha \sum _{n=1}^{N}\beta _n\tilde{D}_n^T\tilde{D}_n+\gamma I)^{-1}(D+\alpha \sum _{n=1}^{N}\beta _n\tilde{D}_n)^Tx. \end{aligned}$$
(17)

Thus, the proof is completed.

After obtaining the optimal coefficient vector \(c^*\), we calculate the reconstruction error of each class

$$\begin{aligned} r_n(x)=\Vert x-D_nc_n^*\Vert _2,n=1,2...,N. \end{aligned}$$
(18)

The minimum reconstruction error criterion determines the label of x as

$$\begin{aligned} \textrm{label}(x)=\arg \min _{n} r_{n}(x). \end{aligned}$$
(19)

The WCCRC classification method is described in Algorithm 2

figure a
figure b
Table 1. Details of seven imbalanced datasets.
Full size table

4 Experimental Results

In this section, several imbalanced datasets from UCI repository [16] are used to verify the effectiveness of the proposed method.

4.1 Datasets and Experimental Setup

During the experiments, we use two binary-class and five multi-class imbalanced datasets to test the performance of our method. The detailed feature information for these datasets is described in Table 1. The class distribution shows the number of samples of each class, and the imbalance rate (IR) indicates the ratio of the number of samples of the most majority classes to the number of samples of the least minority class. As seen from Table 1, the imbalance rates of the used datasets have a large range from 1.10 to 71.51. The higher the imbalance rate, the greater the difficulty of accurate classification.

Table 2. Comparison of F-measure (\(\%\)) between WCCRC and other imbalanced classification methods on seven datasets.
Full size table
Table 3. Comparison of G-mean (\(\%\)) between WCCRC and other imbalanced classification methods on seven datasets.
Full size table

Since the commonly used metrics in balanced classification cannot effectively evaluate imbalanced classification algorithms, we use \(F-measure\) and \(G-mean\) to measure imbalanced classification performance [7]. Whether binary-classification or multi-classification, the larger the \(F-measure\) and \(G-mean\), the better the classification performance. In the experiments, we use the five-fold cross-validation method [17]. Each dataset is randomly divided into five subsets. One subset is selected as the test set, and the remaining four are used as the training set. This method is randomly performed ten times on each dataset, and the average is taken as the final experimental result. In specific experiments, the parameters involved in each comparison model are carefully adjusted to achieve optimal experimental results. For the proposed WCCRC, there are three parameters \(\alpha \), \(\gamma \), \(\delta \) that are important for the performance evaluation of the model. We set the candidate sets of \(\alpha \), \(\gamma \) as \(\{10^{-5},10^{-4},10^{-3},10^{-2},10^{-1}\}\) and the candidate set of \(\delta \) as \(\{1,2,...,10^{1},10^{2},10^{3},10^{4},10^{5}\}\). These three parameters are tuned by a grid search algorithm to obtain the optimal experimental results.

Table 4. The average classification rate (\(\%\)) of all methods on seven datasets.
Full size table

4.2 Comparison with Imbalanced Classification Methods

In this section, we compare WCCRC with the commonly used imbalanced classification methods including RUS [20], ADASYN [10], SMOTE [6], MWMOTE [1], WELM [27], SMOTEENN [2], and EasyEnsemble [20]. Tables 2 and 3 show the comparison results of WCCRC and the competing algorithms in terms of \(F-measure\) and \(G-mean\), respectively. The best experimental results are shown in bold. It can be seen that WCCRC shows the best recognition performance on five out of seven datasets. For the severely imbalanced dataset Ecoli, although WCCRC’s \(F-measure\) is slightly lower than other methods, its \(G-mean\) far exceeds the second best. Particularly, the accuracy of WCCRC on Wine and Newthyroid1 can reach 100\(\%\).

To comprehensively evaluate the classification performance of our method, we calculate the average classification rate of each method on all imbalanced datasets. The comparison results are reported in Table 4. We can find that two undersampling methods RUS and EasyEnsemble are relatively low. Four oversampling algorithms including SMOTE, WMMOTE, ADASYN, and SMOTEENN have a little improvement and obtain comparable classification performance. WELM performs better than the above sampling approaches. Obviously, WCCRC outperforms all compared methods with a high average recognition rate of \(91.12\%\). In summary, our method has great advantages in handling imbalanced classification issue.

5 Conclusion

This paper proposes a weighted competitive-collaborative representation based classifier for imbalanced classification. It solves the problem that CCRC cannot work well on imbalanced datasets. The key idea is to introduce an adaptive class weight learning scheme into the framework of CCRC. It gives greater weights to the minority classes so that the classification results are more fair to the minority classes. The proposed model is efficiently solved with a closed-form solution. Extensive experimental results on several imbalanced datasets verify the effectiveness of the proposed method. In the future, we will consider more efficient and effective weight learning approaches.