Prediction of Airport Pavement Moduli by Machine Learning Methodology Using Non-destructive Field Testing Data Augmentation

Abstract

For the purpose of the Airport Pavement Management System (APMS), in order to optimize the maintenance strategies, it is fundamental monitoring the pavement conditions’ deterioration with time. In this way, the most damaged areas can be detected and intervention can be prioritized. The conventional approach consists in performing non-destructive tests by means of a Heavy Weight Deflectometer (HWD). This equipment allows the measurement of the pavement deflections induced by a defined impact load. This is a quite expensive and time-consuming procedure, therefore, the points to be investigated are usually limited to the center points of a very large mesh grid. Starting from the measured deflections at the impact points, the layers’ stiffness moduli can be backcalculated. This paper outlines a methodology for predicting such stiffness moduli, even at unsampled locations, based on Machine Learning approach, specifically on a feedforward backpropagation Shallow Neural Network (SNN). Such goal is achieved by processing HWD investigation and backcalculation results along with other variables related to the location of the investigation points and the underlying stratigraphy. Bayesian regularization algorithm and k-fold cross-validation procedure were both implemented to train the neural model. To enhance the training, a data analysis technique commonly referred to as data augmentation was used in order to increase the dataset by generating additional data from the existing ones. The results obtained during the model testing phase are characterized by a very satisfactory correlation coefficient, thus suggesting that the proposed Machine Learning approach is highly reliable. Notably, the proposed methodology can be implemented to evaluate the performance of every paved area.

1 Introduction

Airport infrastructure network of a country, whether already developed or developing, is always a strategic asset for economic and social development [1]. It is therefore necessary to guarantee, despite all potential factors of degradation such as ageing, increase in traffic, budget shortfalls and financial constraints as in the pandemic since 2020 [2], a constant performance level so that the service offered may always meet the requirement for safety, efficiency and functionality. In airport infrastructures, great attention is paid to the runway as it is one of the core structure. In order to evaluate the deterioration level of a runway and its maintenance needs with time, both destructive [3] and non-destructive investigation techniques are usually performed. However, a gradual shift to non-destructive [4] testing (NDT) methods has been observed over the years. The former, by requiring borings, cores and excavation pits on an existing runway, require its temporary closure to traffic and cause a huge financial effort as well as service interruption [5]. The latter, on the other hand, thanks to recent hardware and software improvements, provide the possibility to obtain runway structural data without causing any change or damage.

Heavy Weight Deflectometer (HWD) is worldwide acknowledged as the most suitable NDT device to assess the structural capacity of an airport pavement. Such testing machine can successfully simulate the effects produced by aircraft wheel loads on several pavement sections [6]. First, it is necessary to identify an area of interest, defined by means of an impact points grid. Then, at these points, the deflections generated by a mass dropped from a predetermined height are recorded by multiple geophones placed in contact with the runway surface. Starting from these measured deflections, the corresponding stiffness moduli are usually determined by means of a backcalculation process. Using the thickness of the layers under the pavement, the load magnitude and the Multi-Layer Elastic (MLE) theory, it is possible to calculate the theoretical deflections associated with theoretical stiffness moduli. Subsequently, an iterative numerical analysis allows the stiffness layer moduli to vary so that theoretical deflections are progressively adapted to those actually measured in situ. As a consequence, the solution for the layer stiffness moduli is the one corresponding to the better match between the measured and calculated deflections [7].

During the last few years, multiple soft-computing techniques such as Genetic Algorithms (GA) and Artificial Neural Networks (ANNs) [8] are supporting traditional survey techniques to improve analysis both in terms of time and operational costs, as well as providing more accurate and reliable predictions. Although these are non-physically based approaches, such innovative techniques allow large datasets to be processed with such speed and accuracy that similar analyses can even be performed in situ [9]. However, a large initial dataset is necessary to properly train these models.

This paper is aimed to develop a soft-computing tool that, thanks to machine learning algorithms, can enhance the standard backcalculation by allowing to determine the mechanical parameters also in points not directly tested with the HWD. Specifically, a Shallow Neural Network (SNN) has been designed to make predictions about the runway asphalt concrete stiffness modulus (EAC) at any point within the survey grid, by means of innovative algorithms such as Data Augmentation, Bayesian Regularization and k-fold cross validation. The only required input are the deflections measured by HWD, the spatial distribution of the impact points and the layer structure below them, at a limited number of locations. In this way it is possible to obtain fast and accurate predictions of the stiffness modulus values along the runway, immediately identifying most damaged areas, reducing monitoring costs and optimizing maintenance interventions.

2 Materials and Methods

2.1 In Situ Investigation

The case study is a civil airport belonging to the Italian national airport network located 35 km west of Palermo, in Sicily. It has two intersecting runways: the main one, named 07/25, 3326 m long and 60 m wide, and the secondary one, named 02/20, 2074 m long and 45 m wide (Fig. 1).

Fig. 1.

Layout of Palermo airport

On the latter, an experimental campaign was performed to collect deflection data by means of a HWD. The tests involved a portion of the runway 1800 m long (in South-North direction, from header 02 to header 20) and 12 m wide. The grid of interest consisted of points spaced 3 m transversely and 100 m longitudinally for a total of 5 longitudinal measurement lines (starting from the central axis indicated as 0) and 95 total impact points (Fig. 2).

At each point, a mass suspended at a given height was dropped onto a 30-cm diameter circular plate. The impulse load generated had a magnitude of about 140 kN. In addition to the plate, there were also 9 accelerometer transducers in contact with the pavement. The first measured the deflection generated immediately below the loading plate (indicated as $\delta_0$). The deflections denoted progressively as $\delta_1$ up to $\delta_8$ refer to measurements made by transducers placed at 200, 300, 450, 600, 900, 1200, 1500 and 1800 mm from the center of the loading plate.

Fig. 2.

Experimental impact points (black plus sign marker) on the runway 02/20.

By plotting the $\delta_0$ values, a contour map can be obtained (Fig. 3) that immediately provides a clear overview of the pavement areas characterized by the highest deflection values. These areas are known as Touchdown Zones (TDZs) [11] and show deflections up to 900 µm. Such values are double or sometimes even triple with respect to the deflections measured at the ends of the investigation area, highlighting in advance which sections have potentially greater need for maintenance interventions.

Fig. 3.

Contour map of the $\delta_0$ deflections measured at the impact points.

2.2 Backcalculation Process

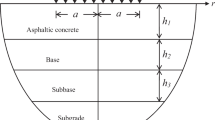
To determine pavement surface layer stiffness modulus, a backcalculation technique was implemented; specifically, a method commonly referred to as Road Moduli Evaluation (RO.M.E.) was used. For backcalculation, the geometry of the pavement structure is needed; therefore, the results of cores and radargrams taken on the investigated area were considered (Fig. 4). Starting from MLE theory laws and assuming the bituminous layer as homogeneous, isotropic and of semi-infinite thickness, the theoretical stress/deformation values at each impact point were then determined. An iterative numerical analysis allowed theoretical deflections to be adjusted so that they became consistent with those measured during the experimental campaign. By reversely solving the problem, it is possible to obtain the stiffness modulus values sought. An exhaustive description of RO.M.E. methodology can be found in Battiato et al. [12].

Fig. 4.

Layer structure under the runway 02/20.

As done with deflections, it is possible to plot the stiffness modulus values thus obtaining the relative contour map (Fig. 5). It can be observed that previously identified TDZs correspond to pavement areas characterized by the lowest modulus values. Conversely, areas characterized by the lowest deflection values show the highest stiffness modulus values. The information described above will be all part of a dataset provided as input to the SNN. However, layers thickness data were converted into a categorical variable named HS; this assumed the same value for the same layer structure, a different value otherwise.

Fig. 5.

Contour map of the backcalculated asphalt concrete stiffness moduli, E_AC.

3 Methodology

3.1 Neural Modelling

Artificial neural networks are one of the most commonly soft-computing techniques used in solving complex problems. Such architectures try to artificially replicate the human brain structure in order to emulate its functioning. Artificial neural networks are usually organized in several layers: in general, the input layer, at least one hidden layer and the output layer are always included. The first one has the task of receiving signals and/or data from outside; the second one is responsible for the real elaboration process whereas the last one collects the elaboration results. An activation function associated with a given layer is intended to modulate the magnitude of the processing result and determine whether or not it should be transmitted to subsequent layers. The number of hidden layers can change depending on the complexity of the problem to be solved. However, an architecture with a single hidden layer (which is called Shallow Neural Network or SNN) is able to solve most fitting problems [13].

The architecture of the proposed SNN has an 8–$n$–1 structure. In fact, there are 8 neurons in the input layer, one for each type of input data: X and Y coordinates of the impact point, the homogeneous section HS, the deflection immediately below the plate ($\delta_0$) and all the deflections between $\delta_2$ and $\delta_5$. The number of neurons belonging to the hidden layer was varied in the range 1–30 and was therefore indicated by the $n$. . Finally, a single neuron belongs to the output layer to represent the asphalt layer stiffness modulus ($E_{{\text{AC}}}$). The best activation function to be assigned to the hidden layer was searched within 4 of the most commonly used in literature [14]: ELU, ReLU, TanH, LogS (Fig. 6). Conversely, the output layer possessed a simple linear activation function. The result was a grid search in order to identify, within the search intervals, the best combination of hidden layer size and activation function that provided the best performance. Finally, the algorithm implemented to train the neural model was Bayesian Regularization. Since input data have very different values and units of measure, their standardization is advisable before being used for model training. For this reason, each data item was subtracted from its respective mean and divided by its respective standard deviation.

3.2 Bayesian Regularization

The training process followed by the proposed SNN is called supervised learning. This means that it starts from a known data set used partly as input and partly as output. The training is made of two fundamental steps:

• 1. the output vector ${\hat{\user2{y}}}$ is calculated starting from the assigned feature vector ${{\varvec{x}}}$;

• 2. the assigned output vector ${{\varvec{y}}}$ is compared with the previously calculated ${\hat{\user2{y}}}$.

The difference between the two vectors is called Loss Function $F\left( {{\hat{\user2{y}}}, {{\varvec{y}}}} \right)$ and it will be used to make the necessary adjustments to the matrix of weights and biases ${{\varvec{W}}}$ so that the subsequent training epochs will lead to better results. Several learning algorithms differ for the mathematical expressions applied to modify ${{\varvec{W}}}$ as a function of the values assumed by $F$ after a fixed number of epochs, $E$.

Fig. 6.

Activation functions. (a) ELU; (b) TanH; (c) ReLU; (d) LogS.

The different algorithms usually start by defining $F$ as Mean Squared Error (MSE):

$$ MSE = \frac{1}{n}\sum \nolimits_1^n {\left( {y_i - \hat{y}_i } \right)^2 } $$

(1)

Using the backpropagation algorithm [15], it is possible to calculate the gradient of $F$ with respect to ${{\varvec{W}}}$. In this way, ${{\varvec{W}}}$ can be subsequently updated in order to minimize the loss value. By indicating with $e$ a generic epoch:

$$ {{\varvec{W}}}^{e + 1} = {{\varvec{W}}}^e - (\nabla^2 F\left( {{{\varvec{W}}}^e } \right))^{ - 1} \nabla F\left( {{{\varvec{W}}}^e } \right) $$

(2)

This expression, recalling the definition of the Levenberg-Marquardt (LM) backpropagation algorithm [16], becomes:

$$ {{\varvec{W}}}^{e + 1} = {{\varvec{W}}}^e - [{{\varvec{J}}}^T \left( {{{\varvec{W}}}^e } \right){{\varvec{J}}}\left( {{{\varvec{W}}}^e } \right) + \mu_e {{\varvec{I}}}]^{ - 1} {{\varvec{J}}}^T \left( {{{\varvec{W}}}^e } \right){{\varvec{v}}}\left( {{{\varvec{W}}}^e } \right) $$

(3)

${{\varvec{I}}}$ stands for the identity matrix while ${{\varvec{J}}}$ represents the Jacobian matrix of $F$ with respect to ${{\varvec{W}}}^e$. Finally, ${{\varvec{v}}}$ represents the error vector, obtained using Eq. 4:

$$ {{\varvec{v}}}({{\varvec{W}}}^e ) = {\hat{\user2{y}}}({{\varvec{W}}}^e ) - {{\varvec{y}}} $$

(4)

$\mu$ is called learning rate and such a scalar defines the algorithm convergence rate. Once a $\mu$ starting value has been set, it is gradually adjusted in order to reach convergence as quickly as possible, without falling into a possible but undesirable local minimum. At the end of the $E$ epochs (or when $\mu$ value exceeds a predefined maximum threshold), the best ${{\varvec{W}}}$ is fixed and kept constant. In this way, assigning as input the ${{\varvec{x}}}$ partitioning intended for the test, loss function value can be determined on a data set not yet processed by the model. Moreover, the proposed SNN has also implemented a technique of ${{\varvec{W}}}$ regularization so that it does not show excessively high weights values. This usually produces good results during the training phase but at the same time bad results during the test phase. Such phenomenon underlines poor generalization capabilities of the model and is more commonly called overfitting.

The aforementioned regularization technique consists in defining the Loss Function as follows:

$$ F_{{opt}} \left( {\user2{\hat{y}}(\user2{W}^{e} } \right),\user2{y},\user2{W}^{e} ) = \beta \user2{\hat{y}}(\user2{W}^{e} ) - \user2{y}_{2}^{2} + \alpha \user2{W}_{{2^{2} }}^{e} $$

(5)

where $F$ is now equal to the sum of the Sum of Squared Errors (SSE), premultiplied by the $\beta$ parameter, and the Sum of Squared Weights (SSW), premultiplied by the $\alpha$ parameter (decay rate). The $\alpha /\beta$ ratio defines the loss function smoothness. The presence of a penalty term forces the weights to be small: in this way, the Loss Function smoothly interpolates the training data keeping good generalization capabilities in the testing phase. For a correct choice of $\alpha$ and $\beta$ parameters David MacKay’s approach was used [17]. Finally, all model hyperparameters were kept equal to their standard values defined within the MATLAB® Toolbox LM algorithm, with the number of epochs $E$ set to 1000.

3.3 k-Fold Cross-Validation

To avoid the undesirable effects related to “hold-out” splitting technique, k-fold cross-validation was implemented in the proposed model. Even before being assigned to the network, the starting dataset was randomly mixed, then divided into k partitions so that each was composed by the same number of elements.

Subsequently k–1 partitions have been used in order to train the model while the remaining one in order to validate it, thus obtaining the relative validation score whose record has been kept. This step has been repeated k times, iteratively so that every fold was used once and once only for the validation. k validation scores were thus obtained: their average provides the general performance of the model.

$$ Val.Score_{CV} = \frac{1}{n}\sum \nolimits_1^n {Val.Score_i } $$

(6)

As suggested by the relevant literature [18], a value of k equal to 5 was used. An illustrative representation of the whole procedure is shown in Fig. 7.

Fig. 7.

Illustrative representation of the k-fold cross-validation procedure.

3.4 Data Augmentation

In order to expand the size of the original dataset, a typical data analysis technique, namely data augmentation, was implemented. This allowed a synthetic dataset to be generated in addition to the original one: it can be used during model training without the need to collect any additional data in the field. Such technique has to be used carefully, since the increased data should never disturb the information resulting from the experimental campaign.

Following this purpose, an interpolation technique has been implemented in order to generate the data that would have been obtained in situ by performing a HWD analysis at the midpoint between two longitudinally successive impact points (Fig. 8). Relevant literature suggests that augmented data should not outnumber experimental data [19]. Therefore, the choice of augmented impact points was taken accordingly and 85 augmented points were identified starting from the 95 experimental ones.

By using this technique, the interpolating function is added to the list of model hyperparameters. In the proposed SNN, a bicubic polynomial function also known as “makima” was chosen; this is particularly appropriate when the points to be interpolated belong to a rectangular grid as those of the case-study. Synthetic data have been used only to train the model. Therefore, the augmented points have been added to the 80% of the known dataset (due to the 5-fold CV), for a total amount of 161 training points.

Finally, the implementation of this technique provides two important evaluations. The first, related to the comparison of the results obtained from the proposed modelling with those that would be obtained using a standard neural model implemented in MATLAB® Toolbox (hereafter referred to as current state-of-practice or CSP SNN). The second, related to the understanding the effects that an experimental campaign with higher points of measurements would have on neural modelling, assuming that the augmented points return information equivalent to the experimental ones.

Fig. 8.

Augmented impact points (red cross marker) on the runway 02/20. (Color figure online)

4 Results and Discussion

Despite the large variability in both measured deflection values and backcalculated moduli, the developed SNN model performed very well. Statistical performance are hereafter measured in terms of R (Pearson Correlation Coefficient), MSE and $R_{adj}^2$ (Adjusted Determination Coefficient). Having denoted the backcalculated stiffness moduli by $E_{AC}$ and the model-predicted stiffness moduli by $\hat{E}_{AC}$, performance indicators are defined as follows:

$$ R(E_{AC} ,\hat{E}_{AC} ) = \frac{1}{n - 1}\sum \nolimits_{i = 1}^n {\left( {\frac{{E_{AC_i } - \mu_{E_{AC} } }}{{\sigma_{E_{AC} } }}} \right)\left( {\frac{{\hat{E}_{AC_i } - \mu_{\hat{E}_{AC} } }}{{\sigma_{\hat{E}_{AC} } }}} \right)} $$

(7)

$$ MSE(E_{AC} ,\hat{E}_{AC} ) = \frac{1}{n}\sum \nolimits_{i = 1}^n {\left( {E_{AC_i } - \hat{E}_{AC_i } } \right)^2 } $$

(8)

$$ R_{adj}^2 (E_{AC} ,\hat{E}_{AC} ) = 1 - \left( {\frac{n - 1}{{n - p}}} \right)\frac{SSE}{{SST}} $$

(9)

$\mu$ and $\sigma$ are the mean and standard deviation, respectively. In addition, $n$ and $p$ indicate the total number of observations and the number of model inputs, respectively.

Table 1. Summary results of the proposed model.

The model that performs best is the one characterized by the 8-13-1 architecture and by a LogS activation function assigned to the hidden layer In general, all the activation functions studied provided satisfactory results, since normally, performances characterized by an R–value higher than 0.8 are representative of a good correlation [20].

The choice of the LogS activation function was particularly suitable in modelling the phenomenon under consideration: even dealing with a number of hidden layer neurons comparable to those of the other models (but much lower than those of ELU SNN), it proved to perform significantly better. Also the $R_{adj}^2$–value was fully satisfactory, demonstrating that the proposed model is able to perform reliable predictions, with small errors, by taking full advantage of the parameters provided as input.

Graphical trends of R and MSE values can be observed in Fig. 9a. These are typical of a correct learning process. In fact, it can be noticed how R increases up until it reaches its maximum value followed by a plateau. Conversely, the MSE decreases until it reaches the minimum value followed by a plateau, too. This is an important indicator that a greater number of hidden layer neurons does not necessarily result in better performance but it may rather imply an unnecessary increase in computational modelling costs.

Figure 9b represents the performance of the best model for each of the 5 folds identified during the pre-processing phase. As explained above, the predictive capabilities shown in Table 1 are the average of the 5 validation scores obtained for each fold shown. The obtained R–value is highly appreciable due to the fact that a CSP SNN modelling would have resulted in a correlation coefficient just equal to 0.9460. Therefore, data augmentation was responsible for increasing this value up to 0.9844 with an overall gain of about 4% on this statistical performance value.

Fig. 9.

(a) Performance metrics of the LogS SNN model; (b) summary of the LogS SNN performance.

This also shows how using a denser grid of investigation points results in higher model performance. The proposed model proved to successfully estimate the current runway state of deterioration and it only took few seconds to process the data. The hardware used refers to a VivoBookPro N580 GD-FI018T equipped with an Intel(R)Core(TM) i7-8750H CPU@2.20 GHz processor and 16GB of RAM. The results obtained can be plotted in the contour map shown in Fig. 10, highlighting which areas presented the lowest stiffness modulus values.

It would have been possible to achieve such a result even by simply interpolating stiffness modulus data obtained from backcalculation. However, in this way the functional link between the modulus and the variables on which it depends would have been ignored. Conversely, the developed methodology respects, at least from a logical point of view, the functional link between the variables involved by requiring deflection measurements, impact point coordinates and layer structure when providing its accurate stiffness modulus predictions.

Fig. 10.

Contour map of the elastic asphalt concrete moduli, E_AC, predicted by the LogS SNN model.

5 Conclusions

This paper aimed at developing a soft-computing methodology for the prediction of the stiffness modulus values of an airport runway asphalt layer. The study was based on the results of an experimental campaign that allowed deflection data to be obtained along with the layer structure under the runway 02/20 of the Palermo airport.

In particular, some innovative machine learning techniques, namely shallow neural networks, have been used. The developed model received as input the deflection values measured by means of the HWD, along with the relative X and Y impact points coordinates, and a categorical variable identifying the stratigraphy. A grid search was performed to identify the best “neurons number – activation function” combination to characterize the hidden layer, resulting in “13 – LogS”. Finally, algorithms such as Bayesian regularization, k-fold cross-validation, and data augmentation were implemented to enhance the predictive capabilities of the proposed model.

Results were very satisfactory, characterized by R and MSE values of 0.9844 and 0.0370, respectively. An additional evaluation metric, namely $R_{adj}^2$, was used to verify that the model correctly and efficiently used the available data and parameters. A value of 0.9493 confirmed these assumptions as well as the goodness of predictive performance. In addition, the comparison with the CSP SNN showed how much data augmentation technique enhanced the developed methodology. A 4% improvement on the correlation coefficient value is a considerable benefit in the context of predictive modelling.

The proposed soft-computing tool has thus proved to be able to accurately predict stiffness modulus values potentially at any point of the runway. Such information is crucial in developing runway maintenance strategies, optimizing both safety and sustainability.

The developed approach can be easily extended to any other airport runway or even to any paved area as long as HWD measurements and stratigraphic information are available.

At the present stage, the proposed methodology fully analyses the current runway deterioration state only and it does not provide the possibility to extend its predictions in time. Further work is required to develop the tool in order to do that. Based on that, future investigations will involve the use, along with the other inputs, of deflection data time-series when available.