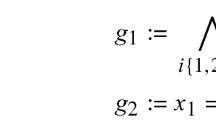Towards the Combination of Model Checking and Runtime Verification on Multi-agent Systems

Abstract

Multi-Agent Systems (MAS) are notoriously complex and hard to verify. In fact, it is not trivial to model a MAS, and even when a model is built, it is not always possible to verify, in a formal way, that it is actually behaving as we expect. Usually, it is relevant to know whether an agent is capable of fulfilling its own goals. One possible way to check this is through Model Checking. Specifically, by verifying Alternating-time Temporal Logic (ATL) properties, where the notion of strategies for achieving goals can be described. Unfortunately, the resulting model checking problem is not decidable in general. In this paper, we present a verification procedure based on combining Model Checking and Runtime Verification, where sub-models of the MAS model belonging to decidable fragments are verified by a model checker, and runtime monitors are used to verify the rest. We present our technique and show experimental results.

1 Introduction

Intelligent systems, such as Multi-Agent Systems (MAS), can be seen as a set of intelligent entities capable of proactively decide how to act to fulfill their own goals. These entities, called generally agents, are notoriously autonomous, i.e., they do not expect input from a user to act, and social, i.e., they usually communicate amongst each other to achieve common goals.

Software systems are not easy to trust in general. Because of this, we need verification techniques to verify that such systems behave as expected. More specifically, in the case of MAS, it is relevant to know whether the agents are capable of achieving their own goals, by themselves or by collaborating with other agents by forming a coalition. This is usually referred to as the process of finding a strategy for the agent(s).

A well-known formalism for reasoning about strategic behaviours in MAS is Al-ternating-time Temporal Logic (ATL) [1]. Before verifying ATL specifications, two questions need to be answered: (i) does each agent know everything about the system? (ii) does the property require the agent to have memory of the system? The first question concerns the model of the MAS. If each agent can distinguish each state of the model, then we have perfect information; otherwise, we have imperfect information. The second question concerns the ATL property. If the property can be verified without the need for the agent to remember which states of the model have been visited before, then we have imperfect recall; otherwise, we have perfect recall.

The model checking problem for ATL giving a generic MAS is known to be undecidable. This is due to the fact that the model checking problem for ATL specifications under imperfect information and perfect recall has been proved to be undecidable [12]. Nonetheless, decidable fragments exist. Indeed, model checking ATL under perfect information is PTIME-complete [1], while under imperfect information and imperfect recall is PSPACE [23]. Unfortunately, MAS usually have imperfect information, and when memory is needed to achieve the goals, the resulting model checking problem becomes undecidable. Given the relevance of the imperfect information setting, even partial solutions to the problem are useful.

Given an ATL formula $\varphi$ and a model of MAS M, our procedure extracts all the sub-models of M with perfect information that satisfy a sub-formula of $\varphi$. Then, runtime monitors are used to check if the remaining part of $\varphi$ can be satisfied at execution time. If this is the case, we conclude at runtime the satisfaction of $\varphi$ for the corresponding system execution. Note that, this does not imply that the system satisfies $\varphi$, indeed future executions may violate $\varphi$. The formal result over $\varphi$ only concerns the current execution, and how it has behaved in it. However, we will present preservation results on the initial model checking problem of $\varphi$ on the model of the system M, as well.

Related Work. Several approaches for the verification of specifications in ATL and $ATL^*$ under imperfect information and perfect recall have been recently put forward. In one line, restrictions are made on how information is shared amongst the agents, so as to retain decidability [10, 11]. In a related line, interactions amongst agents are limited to public actions only [6, 7]. These approaches are markedly different from ours as they seek to identify classes for which verification is decidable. Instead, we consider the whole class of iCGS and define a general verification procedure. In this sense, existing approaches to approximate ATL model checking under imperfect information and perfect recall have either focused on an approximation to perfect information [5, 8] or developed notions of bounded recall [4].

Differently from these works, we introduce, for the first time, a technique that couples model checking and runtime verification to provide results. Furthermore, we always concludes with a result. Note that the problem is undecidable in general, thus the result might be inconclusive (but it is always returned). When the result is inconclusive for the whole formula, we present sub-results to give at least the maximum information about the satisfaction/violation of the formula under exam.

Runtime Verification (RV) has never been used before in a strategic context, where monitors check whether a coalition of agents satisfies a strategic property. This can be obtained by combining Model Checking on MAS with RV. The combination of Model Checking with RV is not new [17]; even though focused only on LTL. Instead, in here, we focus on strategic properties, such as $ATL^*$. Because of this, our work is closer in spirit to [17]; in fact, we use RV to support Model Checking in verifying at runtime what the model checker could not at static time. Finally, in [14], a demonstration paper presenting the tool deriving by this work may be found. Specifically, in this paper we present the theoretical foundations and experimental results behind the tool.

2 Preliminaries

In this section we recall some preliminary notions. Given a set U, $\overline{U}$ denotes its complement. We denote the length of a tuple v as |v|, and its i-th element as $v_i$. For $i \le |v|$, let $v_{\ge i}$ be the suffix $v_{i},\ldots , v_{|v|}$ of v starting at $v_i$ and $v_{\le i}$ the prefix $v_{1},\ldots , v_{i}$ of v. We denote with $v \cdot w$ the concatenation of the tuples v and w.

2.1 Models for Multi-agent Systems

We start by giving a formal model for Multi-agent Systems by means of concurrent game structures with imperfect information [1, 18].

Definition 1

A concurrent game structure with imperfect information (iCGS) is a tuple $M = \langle {Ag}, AP, S, s_I, \{Act_i\}_{i \in {Ag}}, \{\sim _i\}_{i \in {Ag}}, d, \delta , V \rangle$ such that: ${Ag}= \{1,\dots ,m\}$ is a nonempty finite set of agents (or players); AP is a nonempty finite set of atomic propositions (atoms); $S\ne \emptyset$ is a finite set of states, with initial state $s_I \in S$; for every $i \in {Ag}$, $Act_i$ is a nonempty finite set of actions where $Act = \bigcup _{i \in {Ag}} Act_i$ is the set of all actions and $ACT = \prod _{i \in {Ag}} Act_i$ is the set of all joint actions; for every $i \in {Ag}$, $\sim _i$ is a relation of indistinguishability between states, that is, given states $s, s' \in S$, $s \sim _i s'$ iff s and $s'$ are observationally indistinguishable for agent i; the protocol function $d: {Ag}\times S \rightarrow (2^{Act}\setminus \emptyset )$ defines the availability of actions so that for every $i \in Ag$, $s \in S$, (i) $d(i,s) \subseteq Act_i$ and (ii) $s \sim _i s'$ implies $d(i,s) = d(i,s')$; the (deterministic) transition function $\delta : S \times ACT \rightarrow S$ assigns a successor state $s' = \delta (s, \vec {a})$ to each state $s\in S$, for every joint action $\vec {a} \in ACT$ such that $a_i \in d(i,s)$ for every $i \in {Ag}$, that is, $\vec {a}$ is enabled at s; and $V: S \rightarrow 2^{AP}$ is the labelling function.

By Definition 1 an iCGS describes the interactions of a group ${Ag}$ of agents, starting from the initial state $s_I \in S$, according to the transition function $\delta$. The latter is constrained by the availability of actions to agents, as specified by the protocol function d. Furthermore, we assume that every agent i has imperfect information of the exact state of the system; so in any state s, i considers epistemically possible all states $s'$ that are i-indistinguishable from s [13]. When every $\sim _i$ is the identity relation, i.e., $s \sim _i s'$ iff $s = s'$, we obtain a standard CGS with perfect information [1]. Given a set $\varGamma \subseteq {Ag}$ of agents and a joint action $\vec {a} \in ACT$, let $\vec {a}_{\varGamma }$ and $\vec {a}_{\overline{\varGamma }}$ be two tuples comprising only of actions for the agents in $\varGamma$ and $\overline{\varGamma }$, respectively. A history $h \in S^+$ is a finite (non-empty) sequence of states. The indistinguishability relations are extended to histories in a synchronous, point-wise way, i.e., histories $h, h' \in S^+$ are indistinguishable for agent $i \in {Ag}$, or $h \sim _i h'$, iff (i) $|h| = |h'|$ and (ii) for all $j \le |h|$, $h_j \sim _i h'_j$.

2.2 Syntax

To reason about the strategic abilities of agents in iCGS with imperfect information, we use Alternating-time Temporal Logic $ATL^*$ [1].

Definition 2

State ($\varphi$) and path ($\psi$) formulas in $ATL^*$ are defined as follows, where $q \in AP$ and $\varGamma \subseteq {Ag}$:

$$\begin{aligned}&\varphi {:}{:}= q \mid \lnot \varphi \mid \varphi \wedge \varphi \mid \langle \!\langle \varGamma \rangle \!\rangle \psi \\&\psi {:}{:}= \varphi \mid \lnot \psi \mid \psi \wedge \psi \mid X \psi \mid (\psi U \psi ) \end{aligned}$$

Formulas in $ATL^*$ are all and only the state formulas.

As customary, a formula ${\langle \!\langle \varGamma \rangle \!\rangle } \varPhi$ is read as “the agents in coalition $\varGamma$ have a strategy to achieve $\varPhi$”. The meaning of linear-time operators next X and until U is standard [2]. Operators ${[\![ \varGamma ]\!]}$, release R, finally F, and globally G can be introduced as usual. Formulas in the ATL fragment of $ATL^*$ are obtained from Definition 2 by restricting path formulas $\psi$ as follows (where $\varphi$ is a state formula and R is the release operator):

$$\begin{aligned} \psi {:}{:}= X \varphi \mid (\varphi U \varphi ) \mid (\varphi R \varphi ) \end{aligned}$$

We will also consider the syntax of ATL$^*$ in negation normal form (NNF):

$$\begin{aligned}&\varphi {:}{:}= q \mid \lnot q \mid \varphi \wedge \varphi \mid \varphi \vee \varphi \mid {\langle \!\langle \varGamma \rangle \!\rangle } \psi \mid {[\![ \varGamma ]\!]} \psi \\&\psi {:}{:}= \varphi \mid \psi \wedge \psi \mid \psi \vee \psi \mid X \psi \mid (\psi U \psi ) \mid (\psi R \psi ) \end{aligned}$$

where $q \in AP$ and $\varGamma \subseteq {Ag}$.

2.3 Semantics

When giving a semantics to $ATL^*$ formulas we assume agents are endowed with uniform strategies [18], i.e., they perform the same action whenever they have the same information.

Definition 3

A uniform strategy for agent $i \in {Ag}$ is a function $\sigma _i: S^+ \rightarrow Act_i$ such that for all histories $h, h' \in S^+$, (i) $\sigma _i(h) \in d(i, last(h))$; and (ii) $h \sim _i h'$ implies $\sigma _i(h) = \sigma _i(h')$.

By Definition 3 any strategy for agent i has to return actions that are enabled for i. Also, whenever two histories are indistinguishable for i, then the same action is returned. Notice that, for the case of CGS (perfect information), condition (ii) is satisfied by any strategy $\sigma$. Furthermore, we obtain memoryless (or imperfect recall) strategies by considering the domain of $\sigma _i$ in S, i.e., $\sigma _i: S \rightarrow Act_i$.

Given an iCGS M, a path $p \in S^{\omega }$ is an infinite sequence $s_1 s_2\dots$ of states. Given a joint strategy $\sigma _\varGamma = \{\sigma _i \mid i \in \varGamma \}$, comprising of one strategy for each agent in coalition $\varGamma$, a path p is $\sigma _\varGamma$-compatible iff for every $j \ge 1$, $p_{j+1} = \delta (p_j, \vec {a})$ for some joint action $\vec {a}$ such that for every $i \in \varGamma$, $a_i = \sigma _i(p_{\le j})$, and for every $i \in \overline{\varGamma }$, $a_i \in d(i,p_j)$. Let $out(s, \sigma _\varGamma )$ be the set of all $\sigma _\varGamma$-compatible paths from s.

Definition 4

The satisfaction relation $\models$ for an iCGS M, state $s \in S$, path $p \in S^{\omega }$, atom $q \in AP$, and $ATL^*$ formula $\phi$ is defined as follows (clauses for Boolean connectives are immediate and thus omitted):

We say that formula $\phi$ is true in an iCGS M, or $M \models \phi$, iff $(M, s_I) \models \phi$.

Definition 5

Given an iCGS M and a formula $\phi$, the model checking problem concerns determining whether $M \models \phi$.

Since the semantics provided in Definition 4 is the standard interpretation of $ATL^*$ [1, 18], it is well known that model checking ATL, a fortiori $ATL^*$, against iCGS with imperfect information and perfect recall is undecidable [12]. In the rest of the paper we develop methods to obtain partial solutions to this by using Runtime Verification (RV).

2.4 Runtime Verification and Monitors

The standard formalism to specify formal properties in RV is Linear Temporal Logic (LTL) [21]. The syntax and semantics of LTL is the same of $ATL^*$ (Definition 2–4), with state formulas $\varphi {:}{:}=q$ (i.e., no strategic operators are allowed).

Definition 6

(Monitor). Let M be an iCGS and $\psi$ be an LTL property. Then, a monitor for $\psi$ is a function $Mon^{M}_{\psi }:S^+\rightarrow \mathbb {B}_3$, where $\mathbb {B}_3=\{\top , \bot , ?\}$:

$$ Mon^{M}_{\psi }(h) = \left\{ \begin{array}{ll} \top &{} \qquad \forall _{p \in S^\omega } \,\, (M, h \cdot p) \models \psi \\ \bot &{} \qquad \forall _{p \in S^\omega } \,\, (M, h \cdot p) \not \models \psi \\ ? &{} \qquad otherwise.\\ \end{array} \right. $$

where the path p is a valid continuation of the history h in M.

Intuitively, a monitor returns $\top$ if all continuations of h satisfy $\psi$; $\bot$ if all continuations of h violate $\psi$; ? otherwise. The first two outcomes are standard representations of satisfaction and violation, while the third is specific to RV. In more detail, it denotes when the monitor cannot conclude any verdict yet. This is closely related to the fact that RV is applied while the system is still running, and not all information about it are available. For instance, a property might be currently satisfied (resp., violated) by the system, but violated (resp., satisfied) in the (still unknown) future. The monitor can only safely conclude any of the two final verdicts ($\top$ or $\bot$) if it is sure such verdict will never change. The addition of the third outcome symbol ? helps the monitor to represent its uncertainty w.r.t. the current system execution.

2.5 Negative and Positive Sub-models

Now, we recall two definitions of sub-models and some preservation results, defined in [15], that we will use in our verification procedure.

Definition 7

(Negative and Positive sub-models). Given an iCGS $M =$$\langle {Ag}, AP, S, s_I, \{Act_i\}_{i \in {Ag}}, \{\sim _i\}_{i \in {Ag}}, d, \delta , V \rangle$, we denote with $M' = \langle {Ag}, AP,$$S', s_I, \{Act_i\}_{i \in {Ag}}, \{\sim '_i\}_{i \in {Ag}}, d', \delta ', V' \rangle$ a negative sub-model of M, formally $M' \subseteq M$, such that: $S' = S^\star \cup \{s_{t}\}$, where $S^\star \subseteq S$ and $s_I \in S^\star$; $\sim '_i$ is defined as the corresponding $\sim _i$ restricted to $S^\star$; the protocol function is defined as $d'(i,s) = d(i,s)$, for every $s \in S^\star$ and $d'(i,s_{t}) = Act_i$, for all $i \in {Ag}$; given a transition $\delta (s, \vec {a}) = s'$, if $s, s' \in S^\star$ then $\delta '(s, \vec {a}) = \delta (s, \vec {a}) = s'$ else if $s' \in S \setminus S^\star$ and $s \in S'$ then $\delta '(s, \vec {a}) = s_{t}$; for all $s\in S^\star$, $V'(s) = V(s)$ and $V'(s_{t}) = \emptyset$. Furthermore, we denote with $M^* = \langle {Ag}, AP, S', s_I, \{Act_i\}_{i \in {Ag}}, \{\sim '_i\}_{i \in {Ag}}, d', \delta ', V^* \rangle$ a positive sub-model of M, formally $M^* \subseteq M$, such that: $V^*(s) = V(s)$ and $V^*(s_{t}) = AP$.

The intuition behind the above sub-models is to remove the imperfect information by replacing each state involved in $\sim$ with a sink state $s_t$ that under (resp., over) approximates the verification of ATL formulas in negative (resp., positive) sub-models. We conclude this part by recalling two preservation results presented in [15].

Lemma 1

Given a model M, a negative (resp., positive) sub-model with perfect information $M'$ (resp., $M^*$) of M, and a formula $\varphi$ of the form $\varphi = {\langle \!\langle A \rangle \!\rangle } \psi$ (or ${[\![ A ]\!]} \psi$) for some $A \subseteq Ag$. For any $s \in S' \setminus \{s_{t}\}$, we have that:

$$\begin{aligned} M', s \models \varphi \Rightarrow M, s \models \varphi \quad \quad \quad \quad M^*, s \not \models \varphi \Rightarrow M, s \not \models \varphi \end{aligned}$$

3 Our Procedure

In this section, we provide a procedure to handle games with imperfect information and perfect recall strategies, a problem in general undecidable. The overall model checking procedure is described in Algorithm 1. It takes in input a model M, a formula $\varphi$, and a trace h (denoting an execution of the system) and calls the function Preprocessing() to generate the NNF of $\varphi$ and to replace all negated atoms with new positive atoms inside M and $\varphi$. After that, it calls the function FindSub-models() to generate all the positive and negative sub-models that represent all the possible sub-models with perfect information of M. Then, there is a while loop (lines 4–7) that for each candidate checks the sub-formulas true on the sub-models via CheckSub-formulas() and returns a result via RuntimeVerification(). For additional details on Preprocessing(), FindSub-models(), and CheckSub-formulas() see [15].

Now, we focus on the last step, the procedure RuntimeVerification(). It is performed at runtime, directly on the actual system. In previous steps, the sub-models satisfying (resp., violating) sub-properties $\varphi '$ of $\varphi$ are generated, and listed into the set result. In Algorithm 2, we report the procedure performing runtime verification on the system. Such algorithm gets in input the model M, an ATL property $\varphi$ to verify, an execution trace h of events observed by executing the system, and the set result containing the sub-properties of $\varphi$ that have been checked on sub-models of M. First, in lines 2–3, M and $\varphi$ are updated according to the atoms listed in result. This step is used to identify in M and $\varphi$ which sub-formulas have already been verified through CheckSub-formulas(). The two resulting functions are not reported for space constraints, but their full description can be found in [15]. Note that, UpdateFormula() produces two new ATL formulas ($\psi _n$, $\psi _p$), which correspond to the updated version of $\varphi$ for the negative and positive sub-models, respectively. Once $\psi _n$ and $\psi _p$ have been generated, they need to be converted into their corresponding LTL representation to be verified at runtime. This translation is obtained by removing the strategic operators, while leaving the temporal ones (and the atoms). The resulting two new LTL properties $\varphi _n$ and $\varphi _p$ are so obtained (lines 4–5). Finally, by having these two LTL properties, the algorithm proceeds generating (using the standard LTL monitor generation algorithm [3]) the corresponding monitors $Mon^{M'}_{\varphi _n}$ and $Mon^{M'}_{\varphi _p}$. Such monitors are then used by Algorithm 2 to check $\varphi _n$ and $\varphi _p$ over an execution trace h given in input. The latter consists in a trace observed by executing the system modelled by $M'$ (so, the actual system). Analysing h the monitor can conclude the satisfaction (resp., violation) of the LTL property under analysis (w.r.t. the model $M'$). However, only certain results can actually be considered valid. Specifically, when $Mon^{M'}_{\varphi _n}(h) = \top$, or when $Mon^{M'}_{\varphi _p}(h) = \bot$. The other cases, which may include the inconclusive verdict (?), are considered undefined, since nothing can be concluded at runtime. The reason why the conditions in lines 8–9 are enough to conclude $\top$ and $\bot$ directly follow from the following lemmas. The rest of the algorithm is only for storing how the sub-formulas have been verified, whether at runtime (i.e., stored in $\varphi _{rv}$), at static time (i.e., stored in $\varphi _{mc}$), or not at all (i.e., stored in $\varphi _{unchk}$).

We present the preservations results to provide the correctness of our algorithm.

Lemma 2

Given a model M and a formula $\varphi$, for any history h of M starting in $s_I$, we have that:

$$\begin{aligned} Mon_{\varphi _{LTL}}(h) = \top \;\implies \; M,s_I \models \varphi _{Ag}\\ Mon_{\varphi _{LTL}}(h) = \bot \;\implies \; M,s_I \not \models \varphi _{\emptyset } \end{aligned}$$

where $\varphi _{LTL}$ is the variant of $\varphi$ where all strategic operators are removed, $\varphi _{Ag}$ is the variant of $\varphi$ where all strategic operators are converted into ${\langle \!\langle Ag \rangle \!\rangle }$, $\varphi _{\emptyset }$ is the variant of $\varphi$ where all strategic operators are converted into ${\langle \!\langle \emptyset \rangle \!\rangle }$.

Due to the limited space, the proof is omitted. It can be found in [16]. However, it is important to evaluate in depth the meaning of the lemma presented above.

Remark 1

Lemma 2 shows a preservation result from RV to ATL$^*$ model checking that needs to be discussed. If our monitor returns true we have two possibilities: (1) the procedure found a negative sub-model in which the original formula $\varphi$ is satisfied then it can conclude the verification procedure by using RV only by checking that the atom representing $\varphi$ holds in the initial state of the history h given in input; (2) a sub-formula $\varphi '$ is satisfied in a negative sub-model and at runtime the formula $\varphi _{Ag}$ holds on the history h given in input. While case (1) gives a preservation result for the formula $\varphi$ given in input, case (2) checks formula $\varphi _{Ag}$ instead of $\varphi$. That is, it substitutes Ag as coalition for all the strategic operators of $\varphi$ but the ones in $\varphi '$. So, our procedure approximates the truth value by considering the case in which all the agents in the game collaborate to achieve the objectives not satisfied in the model checking phase. That is, while in [5, 8] the approximation is given in terms of information, in [4] is given in terms of memory of strategies, and in [15] the approximation is given by generalizing the logic, here we give results by approximating the coalitions. So, the main limitation of our approach concerns this aspect. Furthermore, we recall that our procedure produces always results, even partial. This aspect is strongly relevant in concrete scenario in which there is the necessity to have some sort of verification results. For example, in the context of swarm robots [19], with our procedure we can verify macro properties such as “the system works properly” since we are able to guarantee fully collaboration between agents because this property is relevant and desirable for each agent in the game. The same reasoning described above, can be applied in a complementary way for the case of positive sub-models and the falsity.

Theorem 1

Algorithm 1 terminates in double-exponential time. Moreover, Algorithm 1 is sound: if the value returned is different from ?, then $M \models \varphi$ iff $k = \top$.

Due to the limited space, the proof is omitted (see [16] for details).

4 Our Tool

The algorithms presented previously have been implemented in Java¹. The resulting tool implementing Algorithm 1 allows to extract all sub-models with perfect information that satisfy a strategic objective from a model given in input. The extracted sub-models, along with the corresponding sub-formulas, are then used by the tool to generate and execute the corresponding monitors over a system execution (Algorithm 2). In more detail, as shown in Fig. 1, the tool expects a model in input formatted as a Json file. This file is then parsed, and an internal representation of the model is generated. After that, the verification of a sub-model against a sub-formula is achieved by translating the sub-model into its equivalent ISPL (Interpreted Systems Programming Language) program, which then is verified by using the model checker MCMAS² [20]. This corresponds to the verification steps performed in CheckSub-formulas() (i.e., where static verification through MCMAS is used). For each sub-model that satisfies this verification step, the tool produces a corresponding tuple; which contains the information needed by Algorithm 2 to complete the verification at runtime. The entire manipulation, from parsing the model formatted in Json, to translating the latter to its equivalent ISPL program, has been performed by extending an existent Java library [9]; the rest of the tool derives directly from the algorithms presented in this paper. The monitors are obtained using LamaConv [22], which is a Java library capable of translating expressions in temporal logic into equivalent automata and generating monitors out of these automata. For generating monitors, LamaConv uses the algorithm presented in [3].

Fig. 1.

Overview of the implemented tool

4.1 Experiments

We tested our tool on a large set of automatically and randomly generated iCGSs. The objective of these experiments was to show how many times our algorithm returned a conclusive verdict. For each model, we ran our procedure and counted the number of times a solution was returned. Note that, our approach concludes in any case, but since the general problem is undecidable, the result might be inconclusive (i.e., ?). In Fig. 2, we report our results by varying the percentage of imperfect information (x axis) inside the iCGSs, from $0\%$ (perfect information, i.e., all states are distinguishable for all agents), to $100\%$ (no information, i.e., no state is distinguishable for any agent). For each percentage selected, we generated 10000 random iCGSs and counted the number of times our algorithm returned with a conclusive result (i.e., $\top$ or $\bot$). As it can be seen in Fig. 2, our tool concludes with a conclusive result more than 80% of times. We do not observe any relevant difference amongst the different percentage of information used in the experiments. This is due to the random nature of the iCGSs used. Moreover, the results we obtained depend on the topology of the iCGSs, so it is very hard to precisely quantify the success rate. However, the results obtained by our experiments using our procedure are encouraging. Unfortunately, no benchmark of existing iCGSs exists, thus these results may vary on more realistic scenarios. Nonetheless, considering the large set of iCGSs we experimented on, we do not expect substantial differences.

Fig. 2.

Success rate of our tool when applied to a set of randomly generated iCGSs

Other than testing our tool w.r.t. the success rate over a random set of iCGSs, we evaluated the execution time as well. Specifically, we were much interested in analysing how such execution time is divided between CheckSub-formulas() and Algorithm 2. I.e., how much time is spent on verifying the models statically (through model checking), and how much is spent on verifying the temporal properties (through runtime verification). Figure 3 reports the results we obtained on the same set of randomly generated ICGSs used in Fig. 2. The results we obtained are intriguing, indeed we can note a variation in the percentage of time spent on the two phases (y-axis) moving from low percentages to high percentages of imperfect information in the iCGSs (x-axis). When the iCGS is close to have perfect information (low percentages on x-axis), we may observe that most of the execution time is spent on performing static verification ($\sim$70%), which corresponds to CheckSub-formulas(). On the other hand, when imperfect information grows inside the iCGS (high percentage on x-axis), we may observe that most of the execution time is spent on performing runtime verification ($\sim$90% in occurrence of absence of information). This behaviour is determined by the number of candidates extracted by the FindSub-models() function. When the iCGS has perfect information, such function only extracts a single candidate (i.e., the entire model), since FindSub-models() generates only one tuple. Such single candidate can be of non-negligible size, and the resulting static verification, time consuming; while the subsequent runtime verification is only performed once on the remaining temporal parts of the property to verify. On the other hand, when the iCGS has imperfect information, FindSub-models() returns a set of candidates that can grow exponentially w.r.t. the number of states of the iCGS. Nonetheless, such candidates are small in size, since FindSub-models() splits the iCGS into multiple smaller iCGSs with perfect information. Thus, the static verification step is applied on small iCGSs and require less execution time; while the runtime verification step is called for each candidate (so an exponential number of times) and is only influenced by the size of the temporal property to verify.

Fig. 3.

How the execution time of our tool when applied to randomly generated iCGSs is divided

In conclusion, it is important to emphasise that, even though the monitor synthesis is computationally hard (i.e., 2EXPTIME), the resulting runtime verification process is polynomial in the size of the history analysed. Naturally, the actual running complexity of a monitor depends on the formalism used to describe the formal property. In this work, monitors are synthesised from LTL properties. Since LTL properties are translated into Moore machines [3], the time complexity w.r.t. the length of the analysed trace is linear. This can be understood intuitively by noticing that the Moore machine so generated has finite size, and it does not change at runtime.

5 Conclusions and Future Work

The work presented in this paper follows a standard combined approach of formal verification techniques, where the objective is to get the best of both. We considered the model checking problem of MAS using strategic properties that is undecidable in general, and showed how runtime verification can help by verifying part of the properties at execution time. The resulting procedure has been presented both on a theoretical (theorems and algorithms) and a practical level (prototype implementation). Note that this is the first attempt of combining model checking and runtime verification to verify strategic properties on MAS. Thus, even though our solution might not be optimal, it is a milestone for the corresponding lines of research. Additional works will be done to improve the technique and, above all, its implementation. For instance, we are planning to extend this work by considering a more predictive flavour.