Bagging-AdaTSK: An Ensemble Fuzzy Classifier for High-Dimensional Data

Abstract

Using fuzzy systems to deal with high-dimensional data is still a challenging work, even though our recently proposed adaptive Takagi-Sugeno-Kang (AdaTSK) model equipped with Ada-softmin can be effectively employed to solve high-dimensional classification problems. Facing high-dimensional data, AdaTSK is prone to overfitting phenomenon, which results in poor performance. While ensemble learning is an effective technique to help the base learners to improve the final performance and avoid overfitting. Therefore, in this paper, we propose an ensemble fuzzy classifier integrating an improved bagging strategy and AdaTSK model to handle high-dimensional classification problems, which is named as Bagging-AdaTSK. At first, an improved bagging strategy is introduced and the original dataset is split into multiple subsets containing fewer samples and features. These subsets are overlapped with each other and can cover all the samples and features to guarantee the satisfactory accuracy. Then, on each subset, an AdaTSK model is trained as a base learner. Finally, these trained AdaTSK models are aggregated together to conduct the task, which results in so-called Bagging-AdaTSK. The experimental results on high-dimensional datasets demonstrate that Bagging-AdaTSK has competitive performance.

1 Introduction

1.1 A Subsection Sample

Fuzzy system is an effective technique to address nonlinear problems, which has been successfully employed in the areas of classification, regression, and function approximation problems [3,4,5]. Takagi-Sugeno-Kang (TSK) fuzzy classifier with interpretable rules has attracted many research interests of the scholars and obtained its significant success [13, 21, 22].

In the fuzzy system, the triangular norm (T-norm) is used to compute the firing strengths of the fuzzy rules, where the product and minimum are two popularly-employed ones [9]. When solving high-dimensional problems, the former most likely causes numeric underflow problem that the result is too close to 0 to be represented by the computer [20]. While the latter is not differentiable, which brings big difficulties to the optimization process. Therefore, using fuzzy systems to solve high-dimensional problems is still a challenging task [15]. Although many of approaches of dimensionality reduction are used and introduced in the design of fuzzy systems [8, 18], this can not tackle the challenge fundamentally.

The approximator of the minimum T-norm, called softmin, is often used to replace it in fuzzy systems since softmin is differentiable [2, 6, 11]. Based on softmin, we proposed an adaptive softmin (Ada-softmin) operator to compute the firing strengths in [20]. Then, the Ada-softmin based TSK (AdaTSK) model was developed, which can be effectively used on high-dimensional datasets without any dimensionality reduction method. Nonetheless, it is prone to overfitting phenomenon when dealing with high-dimensional problems.

Ensemble learning is an effective technique to avoid overfitting phenomenon, which combines some base learners together to perform the given task [23]. It is known to all that the ensemble model outperforms single base learner even though the base learners are weak [12]. Bagging is a representative ensemble method which has been widely used in many real-world tasks [7, 16, 19], in which the base learners are built on bootstrap replicas of the training set. Specifically, a given number of samples are randomly drawn, with replacement, from the original sample set, which are repeated several times to obtain some training subsets. A classifier is trained as a base learner on each training subset. These trained base learners are integrated together using combination method to classify the new points. Obviously, it is possible for some original samples that they are not selected for any subset, which means some information is not used in the classification task. On the other hand, ensemble diversity, that is, the difference among the base learners, is one of the fundamental points of the ensemble learning [1, 14]. However, different bootstrap replicas generated by the aforementioned method may have the same sample, which limits the diversity among the base learners.

In order to enhance the performance of AdaTSK model on dealing with the classification problems, we propose an improved bagging strategy and develop Bagging-AdaTSK classifier by integrating the proposed bagging strategy on AdaTSK. The main contributions are summarized as follows:

• Based on both sample and feature split, an improved bagging strategy is introduced. The subsets partitioned by this improved bagging strategy are capable of covering all the samples and features. On the other hand, each subset contains different samples, which guarantees that the diversity of the base learners is satisfactory.

• We adopt the improved bagging strategy on our recently proposed AdaTSK model and develop an ensemble classifier, Bagging-AdaTSK, which is able to effectively solve high-dimensional datasets. Comparing the original AdaTSK, Bagging-AdaTSK achieves definite improvement on the accuracy.

• The proposed Bagging-AdaTSK model demonstrates superior performance on 7 high-dimensional datasets with feature dimensions varying from 1024 to 7129.

The remainder of this paper is structured as follows. The AdaTSK classifier is reviewed in the first subsection of Sect. 2. Subsections 2.2 and 2.3 introduce the improved bagging strategy and the proposed Bagging-AdaTSK classifier, respectively. Subsection 2.4 analyses the computational complexity of Bagging-AdaTSK. The performance comparison and sensitivity analysis are described in Sect. 3. The Sect. 4 concludes this study.

2 Methodology

In this section, we first review AdaTSK model for classification problems. Secondly, the improved bagging strategy is elaborated. At last, the proposed Bagging-AdaTSK model is introduced.

2.1 AdaTSK Classifier

Consider a classification problem involving D features and $C$ classes. Let a specific sample or data point be represented by ${\mathbf{x}} = \left( {x_{1} ,x_{2} , \cdots ,x_{D} } \right) \in {\mathbb{R}}^{D}$. The number of fuzzy sets defined each feature is denoted by $S$. In this investigation, we adopt so called compactly combined fuzzy rule base (CoCo-FRB) [20] to construct the fuzzy system. As a result, the number of rules, $R$, is equal to $S$. In general, the $r$ th $\left( {r = 1,2, \cdots ,R} \right)$ fuzzy rule of the first-order TSK model with $C$-dimensional output is described as below:

$$ \begin{array}{*{20}c} {{\text{Rule}}_{r} : \,{\text{IF}} \,x_{1} \,{\text{is}}\, A_{r,1} \, {\text{and}}\, \cdots {\text{and}}\, x_{D} \, {\text{is}}\, A_{r,D} ,} \\ {{\text{THEN}}\,y_{r}^{1} \left( x \right)\, = \,p_{r,0}^{1} + \mathop \sum \nolimits_{d = 1}^{D} p_{r,d}^{1} x_{d} , \cdots ,} \\ { y_{r}^{C} \left( x \right) = p_{r,0}^{C} + \mathop \sum \nolimits_{d = 1}^{D} p_{r,d}^{C} x_{d} ,} \\ \end{array} $$

(1)

where ${A}_{r,d} (d=\mathrm{1,2},\cdots ,D)$ is the fuzzy set associated with the $d$th feature used in the $r$th rule, ${y}_{r}^{c}\,\left(\mathbf{x}\right) (c=\mathrm{1,2},\cdots ,C)$ means the output of the $r$th rule for the $c$th class computed from $\mathbf{x}$ and ${p}_{r,d}^{c}$ represents the consequent parameter of the $r$th rule associated with the $d$th feature for the $c$th class. As $R=S$, ${A}_{r,d}$ is also the $r$th $\left(r=\mathrm{1,2},\cdots ,S\right)$ fuzzy set defined on the $d$th feature.

Here, the fuzzy set ${A}_{r,d}$ is modeled by the simplified Gaussian membership function (MF) [5, 20],

$${\mu }_{r,d}\left(\mathbf{x}\right)={e}^{-{\left({x}_{d}-{m}_{r,d}\right)}^{2}},$$

(2)

where ${\mu }_{r,d}\left(\mathbf{x}\right)$ is the membership value of $\mathbf{x}$ computed on ${A}_{r,d}$, ${x}_{d}$ is the $d$th $(d=\mathrm{1,2},\cdots ,D)$ component of $\mathbf{x}$ and ${m}_{r,d}$ represents the center of the $r$th MF defined on the $d$th input variable. Note that the function only uses the $d$th component of $\mathbf{x}$, even though the argument of ${\mu }_{ r,d}$ is shown as $\mathbf{x}$.

In AdaTSK, the firing strength of the $r$th rule, ${f}_{r}(\mathbf{x})$, is computed by Ada-softmin, which is defined as

$${f}_{r}\left(\mathbf{x}\right)={\left(\frac{{\mu }_{r,1}^{\widehat{q}}\left(\mathbf{x}\right)+{\mu }_{r,2}^{\widehat{q}}\left(\mathbf{x}\right)+\cdots +{\mu }_{r,D}^{\widehat{q}}\left(\mathbf{x}\right)}{D}\right)}^{\frac{1}{\widehat{q}}},$$

(3)

where

$$ \hat{q}\, = \,\left\lceil {\frac{{690}}{{\ln \left( {\min \left\{ {\mu _{{r,1}} \left( {\mathbf{x}} \right),\mu _{{r,2}} \left( {\mathbf{x}} \right), \cdots ,\mu _{{r,D}} \left( {\mathbf{x}} \right)} \right\}} \right)}}} \right\rceil , $$

(4)

and $\lceil\cdot \rceil$ is the ceiling function. Note that $\widehat{q}$ is adaptively changed according to the current membership values. Since (3) satisfies the following formula:

$$ \mathop {\lim }\limits_{{\hat{q} \to - \infty }} \left( {\frac{{\mu_{r,1}^{{\hat{q}}} \left( {\mathbf{x}} \right) + \mu_{r,2}^{{\hat{q}}} \left( {\mathbf{x}} \right) + \cdots + \mu_{r,D}^{{\hat{q}}} \left( {\mathbf{x}} \right)}}{D}} \right)^{{\frac{1}{{\hat{q}}}}} = \mathop {\min }\nolimits_{d} \left\{ {\mu_{r,d} } \right\}, $$

(5)

Ada-softmin is an approximator of the minimum operator, in which (4) is used to acquire a proper value of $\widehat{q}$ to help (3) to get the minimum of a group of membership values. Following [20], the lower bound of $\widehat{q}$ is set to −1000 in the simulation experiments. If the $\widehat{q}$ calculated by (4) is less than −1000, we let $\widehat{q}$ be −1000.

The $c$th $(c=\mathrm{1,2},\cdots ,C)$ component of the system output on $\mathbf{x}$ is

$${y}^{c}\left(\mathbf{x}\right)={\sum }_{r=1}^{R}{\overline{f} }_{r}\left(\mathbf{x}\right){y}_{r}^{c}\left(\mathbf{x}\right),$$

(6)

where

$${\overline{f} }_{r}\left(\mathbf{x}\right)=\frac{{f}_{r}(\mathbf{x})}{{\sum }_{i=1}^{R}{f}_{i}({\varvec{x}})},$$

(7)

and

$$ y_{r}^{c} \left( {\mathbf{x}} \right) = p_{r,0}^{c} + \mathop \sum \nolimits_{d = 1}^{D} p_{r,d}^{c} x_{d} , $$

(8)

${\overline{f} }_{r}\left(\mathbf{x}\right)$ is the normalized firing strength of the $r$th rule on $\mathbf{x}$. As described in (1), ${y}_{r}^{c}\left(\mathbf{x}\right)$ is the output of the $r$th rule associated with the $c$th class computed from $\mathbf{x}$.

Fig. 1.

The neural network structure of the first-order TSK fuzzy system.

The neural network structure of the AdaTSK model is shown in Fig. 1. The first layer is the input layer of features. The second layer is the fuzzification layer of which the output is computed by (2) for each node. The third layer is the rule layer, in which D membership values are used together to compute a firing strength by Ada-softmin. The firing strengths are normalized though (7) in the fourth layer. The lower part with two fully connected layers represents the consequent parts behind “THEN” described in (1). Defuzzification process is realized by the last two layers, which is shown in (6).

2.2 The Improved Bagging Strategy

When solving high-dimensional datasets, AdaTSK tends to fall into overfitting dilemma, which reduces the performance. In order to alleviate this issue, we construct an ensemble classifier based on AdaTSK in the framework of an improved bagging strategy. In this section, we introduce this strategy in detail.

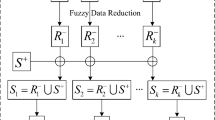
As an effective technique in ensemble learning, bagging randomly draws samples, with replacement, from the original training set to obtain several subsets. Here, we randomly split the samples and features into a group of subsets. Moreover, for each subset, part of samples and features are randomly selected from the remaining subsets to pour into this subset. Consequently, these subsets are overlapped with each other.

Suppose that $N$ data points along with their target labels are contained in the training set, which are represented as

$$\mathbf{U}=\left\{\left({\mathbf{x}}_{1},{z}_{1}\right),\left({\mathbf{x}}_{2},{z}_{2}\right),\cdots ,\left({\mathbf{x}}_{N},{z}_{N}\right)\right\},$$

(9)

where ${\mathbf{x}}_{n}$ and ${z}_{n} (n=1, 2, \cdots , N)$ are the $n$th sample and its target label, respectively. Note that ${\mathbf{x}}_{n}$ is a $D$-dimensional feature vector. The original training set is divided into $K$ subsets by the following two steps.

• 1. The original $N$ training sample with $D$ features are randomly split into $K$ equal subsets (to the extent possible), i.e., $\left\{{{\mathbf{U}}}_{1}, {{\mathbf{U}}}_{2},\cdots ,{{\mathbf{U}}}_{K}\right\}$. The $k$th $(k=\mathrm{1,2},\cdots ,K)$ subset, ${{\mathbf{U}}}_{k}$, contains ${N}_{k}$ samples with ${D}_{k}$ features, where ${N}_{k}<N$ and ${D}_{k}<D$.

• 2. For each ${{\mathbf{U}}}_{k}$, we randomly select a proportion of samples and features from the remaining subsets, $\left\{{{\mathbf{U}}}_{1}, \cdots ,{{\mathbf{U}}}_{k-1},{{\mathbf{U}}}_{k+1},\cdots ,{{\mathbf{U}}}_{K}\right\}$, and integrate them into ${{\mathbf{U}}}_{k}$. Hence, both the number of samples, ${N}_{k}$, and the number of features, ${D}_{k}$, of ${\mathbf{U}}_{k}$ are increased.

By doing this, $K$ subsets that overlap each other are obtained. Although the same original sample is selected by two different subsets, they are not exactly the same as each subset contains a different set of features. Therefore, the ensemble diversity is guaranteed.

For example, assume that 10 samples or features are going to be split into 3 folds, of which the index set is $\left\{ {1,2,3,4,5,6,7,8,9,10} \right\}$. Firstly, this index set is randomly divided into 3 equal subsets to the extent possible, like, $\left\{ {1,5,8,9} \right\}$, $\left\{ {6,7,10} \right\}$ and $\left\{ {2,3,4} \right\}$. For each subset, such as $\left\{ {1,5,8,9} \right\}$, 50% elements of the remaining two subsets are randomly selected and incorporated into it. Then, $\left\{ {1,5,8,9} \right\}$ is extended to $\left\{ {1,2,5,8,9,10} \right\}$. After random selection, the final three subsets are $\left\{ {1,2,5,8,9,10} \right\}$, $\left\{ {3,4,5,6,7,9,10} \right\}$ and $\left\{ {1,2,3,4,6,7,9} \right\}$. The index set mentioned in this example is applicable for sample indices as well as feature indices. Where 50% is explained as the overlap rate. Using the split strategy, a high-dimensional dataset is divided into several low-dimensional subsets. In this investigation, two different overlap rates are set for samples and features, which are denoted by $\rho_{1}$ and $\rho_{2}$, respectively. Assume that $\rho$ is a overlap rate of the samples or features, the proportion of the samples or features contained in a subset to the whole training set is

$$ \gamma = \frac{1}{K} + \frac{K - 1}{K}\rho = \rho + \frac{1 - \rho }{K} $$

(10)

It is obvious that the number of samples or features contained in a subset decreases as $K$ increases. A smaller $K$ means the number of samples or features divided into a subset is more. Both the overlap rates are between 0 and 1, to which the sensitivities are analysed in Sect. 2.

2.3 Bagging-AdaTSK Classifier

In the framework of the improved bagging strategy, $K$ AdaTSK models are independently trained as the base learners. After training, these AdaTSK models are aggregated to predict the target labels. This ensemble classifier is named Bagging-AdaTSK. Several combination methods are popularly used, such as voting and averaging [23]. Comparatively speaking, the final results given by the voting are with more logical interpretability, while the averaging usually achieves better accuracy. Here, the averaging method is used for Bagging-AdaTSK.

Fig. 2.

The framework of Bagging-AdaTSK model.

Suppose that the predicted output of the $k$th AdaTSK on the given sample, ${\mathbf{x}}$, is $\varphi_{k} \left( {\mathbf{x}} \right)$. The system output of Bagging-AdaTSK is.

$$ \varPhi \left( {\mathbf{x}} \right) = \frac{1}{K}\mathop \sum \nolimits_{k = 1}^{K} \varphi_{k} \left( {\mathbf{x}} \right), $$

(11)

where both $\varPhi \left( {\mathbf{x}} \right)$ and $\varphi \left( {\mathbf{x}} \right)$ are $C$-dimensional vector. The framework of the Bagging-AdaTSK is shown in Fig. 2.

Two methods are used to optimize the base learners of the proposed Bagging-AdaTSK. i.e., the gradient descent (GD) algorithm and least square error (LSE) estimation. The loss function of an AdaTSK is defined as

$$ L = \frac{1}{{2N_{k} }}\mathop \sum \nolimits_{n = 1}^{{N_{k} }} \mathop \sum \nolimits_{c = 1}^{C} \left( {y^{c} \left( {{\mathbf{x}}_{n} } \right) - y_{c} \left( {{\mathbf{x}}_{n} } \right)} \right)^{2} , $$

(12)

where $N_{k}$ is the number of training samples in terms of the $k$th base learner, $y^{c} \left( {{\mathbf{x}}_{n} } \right)$ and $y_{c} \left( {{\mathbf{x}}_{n} } \right)$ respectively correspond to the $c$th component of the system output and the true label vector (transformed by one-hot encoding) for the $n$th input instance, ${\mathbf{x}}_{n} \left( {n = 1,2, \cdots ,N_{k} } \right)$. The gradients of the loss function with respect to the centers and consequent parameters are

$$ \begin{array}{*{20}c} {\frac{\partial L}{{\partial m_{r,d} }} = \frac{1}{N}\mathop \sum \nolimits_{n = 1}^{N} \left[ {2\overline{f}_{r} \left( {{\mathbf{x}}_{n} } \right)\left( {x_{n,d} - m_{r,d} } \right)} \right.} \\ { \times \left. {\mathop \sum \nolimits_{c = 1}^{C} \left[ {\left( {y^{c} \left( {{\mathbf{x}}_{n} } \right) - y_{c} \left( {{\mathbf{x}}_{n} } \right)} \right)\left( {y_{r}^{c} \left( {{\mathbf{x}}_{n} } \right) - y^{c} \left( {{\mathbf{x}}_{n} } \right)} \right)} \right]} \right],} \\ \end{array} $$

(13)

and

$$ \frac{\partial L}{{\partial p_{r,d}^{c} }} = \frac{1}{N}\mathop \sum \nolimits_{n = 1}^{N} \left[ {\left( {y^{c} \left( {{\mathbf{x}}_{n} } \right) - y_{c} \left( {{\mathbf{x}}_{n} } \right)} \right)\overline{f}_{r} \left( {{\mathbf{x}}_{n} } \right)x_{n,d} } \right], $$

(14)

respectively, where $x_{n,d}$ is the $d$th component of the sample ${\mathbf{x}}_{n}$. We use the following formula to update them in the $t$th iteration,

$$ \omega^{{\left( {t + 1} \right)}} = \omega^{\left( t \right)} - \eta \frac{\partial L}{{\partial \omega^{\left( t \right)} }}, $$

(15)

where $\omega$ indicates the general parameters of the centers and consequent parts, $\eta > 0$ is the learning rate.

In addition, LSE estimation method is also used to optimize the consequent parameters with fixed antecedents. The elaborate procedure for the LSE estimation is provided in [10]. Hence, we do not provide the formulas for LSE method here.

2.4 The Computation Complexity of Bagging-AdaTSK Classifier

Here we analyse the increment of the computation complexity of Bagging-AdaTSK comparing with AdaTSK. For an AdaTSK classifier, the computational cost in terms of one instance is $O\left( {3DR + \left( {2D + 5} \right)R + 2R + 2DCR + \left( {2R - 1} \right)C} \right)$, i.e., $O\left( {DCR} \right)$, in the forward propagation. Similarly, we can compute the computational complexity for the back-propagation, which is also $O\left( {DCR} \right)$ for each instance. As a consequence, the overall complexity of the AdaTSK is $O\left( {DCR} \right)$.

In the Bagging-AdaTSK, the input dimension of each base learner is denoted by $D_{k} \left( {k = 1,2, \cdots ,K} \right)$ which is smaller than $D$ as the feature space is split. The computation complexity of Bagging-AdaTSK is $O\left( {\mathop \sum \nolimits_{k = 1}^{K} D_{k} CR} \right)$, where $D_{k} = D\left( {\rho_{2} + \left( {1 - \rho_{2} } \right)/K } \right)$. Hence, $O\left( {\mathop \sum \nolimits_{k = 1}^{K} D_{k} CR} \right)$ can be rewritten as $O\left( {\left( {1 + \left( {K - 1} \right)\rho_{2} } \right)DCR} \right)$. Note that $\rho_{2}$ is between 0 and 1 and we set it to a very small value, say 0.01 and 0.001, in the high-dimensional tasks. On the other hand, $K$ is the number of base learners defined by the user, of which the value is not big. Therefore, it can be concluded that the computation complexity increment of Bagging-AdaTSK is not large comparing with the original AdaTSK.

Table 1. Summary of the 7 classification datasets.

3 Simulation Results

To demonstrate the effectiveness of Bagging-AdaTSK, it is tested on 7 datasets with feature dimensions varying from 1024 to 7129, which are regarded as high-dimensional datasets according to [20]. Table 1 summarizes the information of these datasets, which includes the number of features (#Features), the number of classes (#Classes) and, the size of dataset.

Table 2. The classification results of RF, SVM, BLS, AdaTSK, and three Bagging-AdaTSK models with different optimization strategies.

3.1 The Classification Performance of Bagging-AdaTSK

In our experiments, three fuzzy sets are defined on each feature for all these 7 datasets, i.e., $R = S = 3$. The centers of the membership functions are evenly placed on the interval $\left[ {x^{min} , x^{max} } \right]$ for each feature, where $x^{min}$ and $x^{max}$ are the minimum and maximum value of a feature on the input domain. Specifically, the centers are initialized by

$$ m_{r,d} = x_{d}^{min} + \left( {x_{d}^{max} - x_{d}^{min} } \right)\frac{r - 1}{{R - 1}}, $$

(16)

where $r = 1,2, \cdots ,R$, $d = 1,2, \cdots ,D$, $x_{d}^{min}$ and $x_{d}^{max}$ represent the minimum and maximum value of the $d$th feature on the input domain. Since three fuzzy sets are defined on each feature, the values of the centers initialized for the $d$th feature is $\left\{ {x_{d}^{min} ,\frac{{x_{d}^{min} + x_{d}^{max} }}{2},x_{d}^{max} } \right\}$. All consequent parameters are initialized to zero.

We build 10 base learners in Bagging-AdaTSK, i.e., $K = 10$. In other words, 10 AdaTSK classifiers are trained in the framework of the improved bagging strategy. On the other hand, two overlap rates, $\rho_{1}$ and $\rho_{2}$, need to be set in Bagging-AdaTSK. According to (10), if bigger $\rho$ is used, the proportion of the samples or features contained in a subset to the whole training set is bigger. We wish that each subset has enough, but not too many, samples or features to help AdaTSK classifier to achieve satisfactory performance. For the datasets listed in Table 1, their sample sizes are small and the feature dimensions of them are high. Therefore, $\rho_{1}$ and $\rho_{2}$ are artificially set to 0.5 and 0.01, respectively. The sensitivity of Bagging-AdaTSK to the overlap rates is analysed in the next subsection. Ten-fold cross-validation mechanism [3, 17] is employed in the simulations, which is repeated 10 times to report the average classification performance of Bagging-AdaTSK.

The classification results of Bagging-AdaTSK are compared with those of four algorithms, i.e., Random Forest (RF), Support Vector Machine (SVM), Broad Learning System (BLS) and AdaTSK, on the 7 high-dimensional datasets listed in Table 1. Three fuzzy sets or rules are used in AdaTSK model and each base leaner of Bagging-AdaTSK. Since 10 base learners are contained in Bagging-AdaTSK, which means total 30 rules are used in Bagging-AdaTSK. Correspondingly, 30 trees are adopted for RF. The comparison results are reported in Table 2, where the best results are marked in bold.

Using different optimization strategies for Bagging-AdaTSK, three groups of results are obtained. In Table 2, the results listed in the first two columns of Bagging-AdaTSK are acquired by only optimizing the consequent parameters, for which GD and LSE method are used, respectively. As for the third column under Bagging-AdaTSK in Table 2, both the centers and consequent parameters are updated by GD method.

From Table 2, it is easy to conclude that Bagging-AdaTSK outperforms both RF and AdaTSK classifier no matter which aforementioned optimization strategy is used. Therefore, the proposed bagging strategy is effective and helps AdaTSK model to achieve better results. Among three groups of results in terms of Bagging-AdaTSK, the second one is the best. In other words, fixing the antecedents and using LSE to estimate the consequent parameters is the best optimization strategy for Bagging-AdaTSK when solving high-dimensional data. Comparing the first group of result with the third group of result of Bagging-AdaTSK, the conclusion that optimizing the centers improves the classification performance is drawn. However, optimizing the antecedents increases the computational burden. How to efficiently optimize the antecedents needs to be further studied.

Fig. 3.

The sensitivity of Bagging-AdaTSK to the overlap rates.

3.2 Sensitivity of Bagging-AdaTSK to the Overlap Rates

Since the sample and feature overlap rates, i.e., $\rho_{1}$ and $\rho_{2}$, are the specific parameters to Bagging-AdaTSK, we investigate the sensitivity of the model to them in this section. As described in Subsect. 3.1, the second optimization strategy of Bagging-AdaTSK is the best. Therefore, the analysis of the sensitivity to these two overlap rates is based on LSE method.

Both sample and feature overlap rates are set to the values of

$$ \left\{ {0, 0.05, 0.1, 0.15, \cdots , 0.95} \right\}. $$

When we observe the sensitivity to the sample overlap rate, the feature overlap rate is set to 0.01. On the other hand, $\rho_{1}$ is set to 0.5 when the sensitivity to the sample overlap rate is investigated. The average classification testing accuracies on 10 repeated experiments are shown in Fig. 3, where Fig. 3 (a) and Fig. 3 (b) correspond to the sample overlap rate and feature overlap rate, respectively.

As shown in Fig. 3 (a), Bagging-AdaTSK is not sensitive to the sample overlap rate when $\rho_{1}$ is greater than 0.3. While in the interval, the classification performance increases appreciably, especially on ORL, ARP and PIE datasets. An interesting observation is that each dataset among these three ones contains more classes than the others of four datasets listed in Table 1. Perhaps, when we conduct the classification task involving more classes, more samples are needed, which deserves further study. Additionally, if the sample overlap rate is set to 0, the classification accuracies are not very satisfactory on most of the datasets. This means that it is necessary to let the subsets overlap each other so that each subset contains more samples.

From Fig. 3 (b), it can be seen that the classification performance of Bagging-AdaTSK does not vary greatly with $\rho_{2}$. Hence, Bagging-AdaTSK is not sensitive to the feature overlap rate. Moreover, on the ORL and ARP datasets, the accuracy is lower with $\rho = 0$ than with other values, which denotes that the feature overlap rate is helpful. Since the datasets used here are with thousands of features, a small value of $\rho_{2}$, say 0.01 and 0.05, is recommended in order to reduce the computational burden.

4 Conclusion

Focusing on improving the classification performance of AdaTSK model, we propose an ensemble classifier called Bagging-AdaTSK. Firstly, an improved bagging strategy is introduced, in which the original dataset is split into a given number of subsets from the view of the samples and features. These subsets contain different samples and features which are overlapped with each other. Then, an AdaTSK classifier is trained on each subset. After training, these AdaTSK classifiers are combined by the averaging method to obtain the final predicted labels. Bagging-AdaTSK classifier is suitable for solving high-dimensional datasets as they can be divided into several of low-dimensional datasets to be handled. In our experiments, Bagging-AdaTSK are tested on 7 datasets with feature dimensions varying from 1024 to 7129. The simulation results demonstrate that our proposed Bagging-AdaTSK is very effective and outperforms its four counterparts, RF, SVM, BLS and AdaTSK classifier. In addition, we analyse the sensitivity of Bagging-AdaTSK to the sample and feature overlap rates. The investigation results claim that the proposed model is not sensitive to the them. How to adaptively determine the optimal values of the two overlap rates depending on different problems is going to be further studied in the future work. Besides, we plan to develop more efficient algorithm to optimize the antecedent parameters to improve the performance of Bagging-AdaTSK.