Keywords

1 Introduction

Since its discovery, functional magnetic resonance imaging (fMRI) has been fundamental in understanding the complex processes underlying the time-varying metabolic activation of particular areas of the human brain, in different physio-pathological states and experimental conditions, both in response to tasks and in resting conditions (the so-called resting state fMRI, RS-fMRI) [1, 2]. This technique is widely applied especially when it is not possible to directly interact with or let the patient perform the task, such as with pediatric, sedated and/or neurologically compromised patients [3,4,5]. In fact, recent studies have shown how the brain is essentially driven by intrinsic activity, not related to mental task-, sensory- or motor-induced stimulation and consuming the most of brain energy demand, and that external stimulus can only modulate but not determine its trend. RS-fMRI functional brain connectivity patterns have been investigated also in clinical settings to provide an assessment for diagnosis, prognosis, and treatment of individual patients.

The functional behavior of multiple resting state networks (RSN) has been assessed in the context of end-stage organ disease patients compared to healthy controls and surgical neuro-oncology planning, using the tools of graph theory, seed-based analysis and basic measures of functional connectivity such as Pearson correlation [5, 6] or other techniques such as dynamic causal model for assessing effective connectivity [7, 8]. Specifically, the Pearson correlation coefficient quantifies the strength of the linear pairwise interactions between two variables or groups of variables, e.g. two subsets of voxels in the case of fMRI data. The correlation coefficient has been often employed to assess the degree of interdependency between different areas of the brain in the context of functional connectivity [5, 6]. On the other hand, the directionality of pairwise interactions has been assessed through effective connectivity approaches which investigate the direction of the information flow exchanged between two different brain areas [7, 8]. In this context, RS-fMRI has allowed to identify specific spontaneous activity patterns or modifications that can be associated with the changing of neurologic deficits due to organ diseases or after surgery. Such activity patterns are often described and graphically displayed by a circular graph named “connectome”, consisting of a set of nodes representing brain areas and edges depicting their multiple interconnections [9, 10].

The analysis of the human connectome based on RS-fMRI measurements is a consolidated but also evolving research field, where several methodological issues still need to be addressed. A main question is which type of measure to adopt to quantify connectivity and how to assess the significance of the measured connections. Several studies report the use of thresholding methods applied to bivariate correlation measures to select only the most relevant connections within these complex networks, but in the literature an unequivocal way to set the optimal threshold has still not been identified [11, 12]. Moreover, it has been shown that the threshold selection may strongly depend on the algorithms used to identify intrinsic component networks (ICN) and on the size of the whole analyzed network. ICNs are groups of independent components (IC), extracted from RS-fMRI images through independent component analysis (ICA) [13], and are indicative of different areas of the brain which can be anatomically separated but are activated synchronously (i.e., they are temporally coherent), following the same oscillation patterns in resting-state conditions. Another emerging issue is the need to use connectivity measures which go beyond the framework of pairwise interactions. Approaches such as the Pearson correlation or dynamic causal modeling are, indeed, confined to a bivariate framework which does not take into account higher-order interactions, i.e. interactions involving more than two variables or groups of variables. It is indeed increasingly evident that complex brain networks such as those probed by RS-fMRI recordings display emergent behaviors which cannot be described solely in terms of the interaction between pairs of network nodes. To address such complex high-order interactions, new measures typically devised within the frame of information theory, are being defined and increasingly used in multivariate biomedical datasets [14,15,16].

In this work, starting from the consolidated concept of mutual information (MI), which quantifies the amount of information shared between groups of random variables, we have applied recently defined measures of static interdependence (i.e., interdependence between equal-time points in two time series) for assessing high-order redundant and synergistic contributions brought by adding a target ICN to a source system already composed of a given number of ICNs [14,15,16]. Specifically, in broad terms, while synergy arises from statistical interactions that can be found collectively in a network but not in parts of it considered separately, redundancy refers to group interactions that can be explained by the communication of sub-groups of scalar or vector variables. In this way, we are able to assess and describe brain interactions occurring at higher orders, i.e. between more than two brain areas, thus overcoming the limitations of the above-indicated approaches that instead operate mostly pairwise. Mostly redundant connectivity patterns were identified in our analyses and their statistical significance was assessed through surrogate data testing, without the need for applying arbitrary thresholding procedures.

2 Materials and Methods

2.1 Dataset

In this study, we used a subset of the public database WU-Minn HCP 1200 Subjects Data Release from Human Connectome Project (HCP), that includes high-resolution 3T MR scans from young healthy adult twins and non-twin siblings (ages 22–35) using four imaging modalities: structural images (T1w and T2w), RS-fMRI, task-fMRI (t-fMRI), and high angular resolution diffusion imaging (d-MRI). RS-fMRI scans were acquired in a darkened room for approximately 15 min, for a total of about 1200 frames per run.

Subjects were asked to stay with eyes open relaxingly fixating on a projected white crosshair on a dark background. Images were collected using the acquisition parameters indicated in Table 1. For further details we refer the reader to [17].

Table 1. RS-fMRI acquisition settings [17].
Full size table

2.2 Data Processing and Independent Component Analysis

The dataset was processed first with the minimal preprocessing pipelines for the Human Connectome Project [18], and then with a smoothing algorithm using a Gaussian kernel of 6 mm Full Width at Half Maximum (FWHM). After this preprocessing pipeline, RS-fMRI data were decomposed using the common technique of independent component analysis (ICA). Group ICA of fMRI Toolbox (GIFT, http://icatb.sourceforge.net) [13, 19, 20], performed using the Infomax algorithm [21], was used to compute C = 100 spatially independent components (ICs). After spatial reconstruction and visual inspection of the 100 components, C′ = 53 components-of-interest, with anatomical distribution schematized in Table 2, were selected for this work.

Table 2. ICN decomposition of the RS-fMRI.
Full size table

2.3 Static O-Information

This section presents the framework to measure static interactions among \(Q\) stationary random variables \({\varvec{X}} = \left\{ {X_{1} , \ldots ,X_{Q} } \right\}\), grouped in \(M\) blocks \({\varvec{Y}} = \left\{ {Y_{1} , \ldots ,Y_{M} } \right\}\). The \(i^{th}\) block has dimension \(M_{i}\), so that \(Q = \sum\nolimits_{i = 1}^{M} {M_{i} }\). The activity of the complex network formed by the \(M\) interacting systems can be described by the mutual information (MI) between blocks, here denoted as \(I_{{Y_{i} ;Y_{j} }}\) when computed for the two vector variables \(Y_{i}\) and \(Y_{j}\). Higher-order interactions are assessed by means of the O-Information (OI), a novel measure which generalizes the MI to groups of variables [14,15,16]. The OI of \(N\) random vectors taken from the set \({\varvec{Y}} = \left\{ {Y_{1} , \ldots ,Y_{M} } \right\}\) is defined as:

$$ \Omega_{{Y^{N} }} = \Omega_{{Y_{ - j}^{N} }} + \Delta_{{Y_{ - j}^{N} ;Y_{j} }} , $$
(1)

where \(Y^{N} = \left\{ {Y_{{i_{1} }} , \ldots ,Y_{{i_{N} }} } \right\}\), \(i_{1} , \ldots ,i_{N} \in \left\{ {1, \ldots ,M} \right\},N \le M\), is the analyzed group of random vectors, \(Y_{ - j}^{N} = Y^{N} \backslash Y_{j}\) is the subset of random vectors where \(Y_{j}\) is removed (\(j \in \left\{ {i_{1} , \ldots ,i_{N} } \right\}\)), and where the quantity

$$ \Delta_{{Y_{ - j}^{N} ;Y_{j} }} = \left( {2 - N} \right)I_{{Y_{ - j}^{N} ;Y_{j} }} + \sum\nolimits_{\begin{subarray}{l} m \ne 1 \\ m \ne j \end{subarray} }^{N} {I_{{Y_{ - mj}^{N} ;Y_{j} }} } $$
(2)

is the variation of the OI obtained with the addition of \(Y_{j}\) to \(Y_{ - j}^{N}\), being \(Y_{ - mj}^{N} = Y^{N} \backslash \{ Y_{j} ,Y_{m} \}\). In this framework, if the sign of the OI increment is positive (\(\Delta_{{Y_{ - j}^{N} ;Y_{j} }} > 0\)) the information brought by \(Y_{j}\) to \(Y_{ - j}^{N}\) is redundant, while a negative OI increment means that the influence of \(Y_{ - j}^{N}\) on \(Y_{j}\) is dominated by synergy. In other words, if OI > 0 the system is redundancy-dominated, while OI < 0 means that the system is synergy-dominated; if OI = 0, synergy and redundancy are balanced in the analyzed network. Note that, since \(\Omega_{{Y^{2} }} = 0\) for any pair of variables, when \(N = 3\) random vectors are considered, i.e. \({\varvec{Y}} = \left\{ {Y_{i} ,Y_{k} ,Y_{j} } \right\}\), the OI in (1) reduces to the OI increment:

$$ \Delta_{{Y_{i} ,Y_{k} ;Y_{j} }} = - I\left( {Y_{j} ;Y_{i} ,Y_{k} } \right) + I\left( {Y_{j} ;Y_{i} } \right) + I\left( {Y_{j} ;Y_{k} } \right), $$
(3)

In this case, the OI increment in (3) coincides with the well-known interaction information, measuring the difference between synergy and redundancy when a target variable is added to a bivariate source vector process [22].

The calculation of the measures (1) and (2) requires an approach to compute the MI between vector random variables. In this work, assuming that the observed variables have a joint Gaussian distribution, we exploit the linear parametric representation to compute MI [23]. Specifically, we consider two generic zero-mean vector variables \(Z_{1}\) and \(Z_{2}\) containing respectively \(n\) and \(m\) random variables with a number \(t\) of observations, assuming that \(Z_{1}\) and \(Z_{2}\) take the role of \(Y_{j}\) and \(Y_{ - mj}^{N}\) in (2). The two variables are related by the following linear regression model:

$$ Z_{1} = AZ_{2} + U, $$
(4)

where variable \({Z}_{1}\) is predicted using an \(n\times m\) coefficient matrix \(A\) which weights the regressors \({Z}_{2}\), and \(U\) is a vector of \(n\) zero-mean white noises (prediction errors)\(.\) In this context, the MI between the two variables, which is defined as [24]:

$$ I_{{Z_{1} ;Z_{2} }} = H\left( {Z_{1} } \right) - H(Z_{1} |Z_{2} ), $$
(5)

can be estimated exploiting the relation between entropy and variance valid for Gaussian variables, i.e. expressing the entropy of the predicted variable as \(H\left( {Z_{1} } \right) = \frac{1}{2}log\left( {\left( {2\pi e} \right)^{n} \left| {\Sigma_{{Z_{1} }} } \right|} \right)\) and the conditional entropy of the predicted variables given the predictor as \(H\left( {Z_{1} {|}Z_{2} } \right) = \frac{1}{2}log\left( {\left( {2\pi e} \right)^{n} \left| {\Sigma_{U} } \right|} \right)\) , where \(\Sigma_{{Z_{1} }}\) is the \(n \times n\) covariance of the predicted variable and where \(\Sigma_{U}\) is the \(n \times n\) covariance of the prediction errors [25].

2.4 Data Analysis and Statistical Analysis

Static interactions among \(Q = 53\) stationary random variables of length \(t = 1195\) observations, which are realizations of the 53 selected ICs, grouped in \(M = 7\) blocks representing the 7 identified ICNs \(Y_{1} , \ldots ,Y_{7}\) (Table 2), were investigated. The functional connectivity between groups of ICNs, from order \(N = 2\) to order \(N = M = 7\), was assessed through exploitation of the MI and of the novel OI measure defined in Sect. 2.3. We performed ordinary least squares identification of the linear regression models defined as in (4) to assess the pairwise interaction (\(N = 2\)) between two ICNs through the MI measure, as well as to assess higher-order interactions through the OI measure computed for orders \(N\) from 3 to 7 considering all possible combinations of ICNs, herein referred to as “multiplets”. Specifically, we analyzed the following number of multiplets: 35 of order \(N = 3\); 35 of order \(N = 4\); 21 of order \(N = 5\); 7 of order \(N = 6\); 1 of order \(N = M = 7\).

Surrogate data analysis was carried out to evaluate the number of subjects whose MI and OI values were statistically significant. Specifically, 20 surrogates were generated according to a circular shift procedure which randomly shifts in time the ICs data for each given subject. For each ICN, the lag of the shifted samples (k) was chosen randomly between 10 and 1010 in order to ensure a larger variability of the shift, and this k was chosen the same for each IC belonging to the ICN. This choice was done to maintain within-network interdependencies (i.e., interactions among the scalar components of the vector variable \(Y_{i}\)), while destroying dependencies between different networks (i.e., interactions between any pair of variables taken from \(Y_{i}\) and \(Y_{i}\), \(i,j = 1, \ldots ,7\)). The resulting surrogates are realizations of independent identically distributed random variables with the same marginal probability distribution as the original variables under analysis, but with destroyed correlation structure [26]. When the maximum value of the considered measure (MI or |OI|) among all the surrogates computed for a given subject was less than the same measure computed on the original time series for the same subject, we considered this measure as significant and added the subject to the total number of significant ones.

To investigate statistical differences between different multiplets within the same order, we carried out a Student t-test for paired data and corrected for multiple comparisons using the Bonferroni-Holm correction. Since the number of paired combinations was found to be extremely high, especially for low orders where the number of multiplets was higher, we focused the analysis only on a subset of multiplets. Specifically, triplets (multiplets of order \(N = 3\)) were chosen where the Default Mode (DM) was present, while higher-order multiplets (orders from the \(4^{th}\) to the \(6^{th}\); the \(7^{th}\) order was not considered as constituted by a single multiplet) were selected as those combinations whose roots of \(3^{th}\), \(4^{th}\) and \(5^{th}\) order contained the DM component [27, 28]. In this way, we identified 15, 19, 12 and 3 multiplets for orders \(3^{th}\), \(4^{th}\), \(5^{th}\) and \(6^{th}\) to analyze, respectively.

3 Results and Discussion

Figure 1(a) and 1(b) display two connectograms, whose edges map functional connections between different ICNs in terms of MI values (Fig. 1(a)) or number of subjects who showed statistically significant MI values (Fig. 1(b)). The application of surrogate data analysis led us to statistically validate our measures. With reference to Fig. 1(b), we found a significant percentage of MI values for pairs of ICNs in the interval [90–100] %. Despite results regarding significant subjects in OI measures are not shown here for brevity, significant percentages between 50% and 100% were reported for multiplets of order 3, while percentages between 95% and 100% were found for multiplets of order 4. Full significance (100%) was detected for multiplets of higher order.

Fig. 1.
figure 1

Connectomic map. Edges represent functional connections between different ICNs in terms of MI values averaged on the whole set of subjects (panel a)) or number of significant subjects (panel (b)), while the 7 nodes represent the ICNs identified through ICA.

Full size image

This finding shows that higher-order interdependencies, characterized by higher redundancies as shown in Fig. 2, are much more significant than lower order connectivity patterns. The reason for this increase may be related to the increasingly stronger connectivity which characterize the structure of higher order network interdependencies. Figure 1(a) depicts that links between DM and CC (i.e. Cognitive Control) networks, between CC and SM (i.e. Sensorimotor) networks and between CC and VS (i.e. Visual) networks are characterized by the highest MI values. With reference to Table 2 and Fig. 3, these networks, described by the index 3 for CC, 4 for DM, 6 for SM and 7 for VS, are mostly connected with redundant pathways.

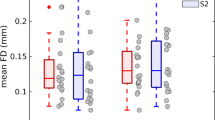
The distribution of the O-Information index as a function of the order of the interaction is depicted in Fig. 2, where each grey dot represents the value of the interaction averaged on all the 823 subjects for each multiplet. Increasing the interaction order leads to find an increase in redundancy within the considered network. Indeed, the type of information brought by an ICN when it is added to a lower-order network seems to become more and more redundant with increasing numbers of analyzed ICNs, suggesting that high order group interactions can be better explained by the communication of sub-groups.

Fig. 2.
figure 2

Distributions and individual values (averaged over 823 subjects) of the O-Information computed for each multiplet as a function of the interaction order N. Each point represents a given multiplet intended as a combination of ICNs. Darker and light blue areas represent 1 standard deviation and 95% confidence interval, respectively, while red line is the mean value of the distribution.

Full size image

Figure 3(a), b), (c) and (d) show the distributions of the O-Information values of order 3, 4, 5 and 6, respectively, for all the multiplets specified in Sect. 2.4, and results of statistical analyses. The t-test revealed the presence of significant differences between the OI values of most pairs of multiplets, while only a few pairs of combinations were found to have mean OI values not significantly different between each other; these pairs are connected in the figure with red dashed lines. While it remains clear that increasing the order interaction leads to higher redundancy, the interpretation of the differences between OI values obtained from different combinations of ICNs is not straightforward. The addition of a given ICNs to pre-existing networks may cause diverse redundancy fluctuations in the same subjects. In other words, starting from a given combination of ICNs, an additional ICN inserted among those remaining generates a specific redundancy increment which is peculiar to that ICN and is different from the one that would be produced inserting another ICN. Such behavior suggests that high-order interactions between cerebral areas are very complex and strongly depend on the brain connections under analysis.

Specifically, our results show that higher redundant contributions were found for multiplets containing as “root” system the ICNs CC and DM, with addition of ICNs SC (Subcortical), SM (Sensorimotor) and VS (Visual) as also demonstrated in Fig. 1, where the highest values of MI were found between these networks. Then, the complex and high order communications between these subsets of ICNs seem to be responsible for most of the redundancy patterns found in our analyses. A main limitation of our analysis consists in the difficult interpretation of the results from a physiological point of view and the inability of generalization of the results, given the absence of a control condition to refer to.

Fig. 3.
figure 3

Distributions and individual OI values for different multiplets of order 3 (a), 4 (b), 5 (c) and 6 (d). Darker and light blue areas represent 1 standard deviation and 95% confidence interval, respectively, while red line is the mean value of the distribution. With reference to Table 2, each ICN is indicated by a number as follows: (1) AD; (2) CB; (3) CC; (4) DM; (5) SC; (6) SM; (7) VS. Pairwise t-tests showed statistical differences for most pairs of distributions, except for those highlighted by red dashed lines.

Full size image

4 Conclusion

In this work we computed measures of high-order interaction between vector-valued variables for the evaluation of the information shared between several pairs of RSNs in the brain. With respect to the common methodologies found in the literature, mostly based on the use of Pearson correlation and on thresholding approaches for the selection of the most significant connectivity links [6, 11, 12], our tools allow to detect redundancy and synergy in complex systems starting from the well-known measure of mutual information [14,15,16]. In this context, O-Information measures provide additional information if compared to the Pearson correlation index and other pairwise functional connectivity measures. In our work, calculation of the O-Information has allowed us to investigate the complex higher-order structures consisting not only in just single pairs of voxel subsets, but instead multiplets of voxel subsets which share multivariate information. The assessment of the statistical significance of the interactions of any order was performed through surrogate data testing in place of selecting an adequate threshold, a procedure which strongly depends on the methodology used to extract ICNs and lacks standardization.

We found that RSNs are dominated by redundant interdependencies which tend to increase in strength as the order of the analyzed interaction grows. In particular, multiplets containing CC, DM, SM and VS networks show highest values of MI and mostly redundant trends over all the orders of OI measures. Physiological interpretations of the obtained findings are not straightforward, especially because the underlying mechanisms constitute the basis of the human brain activity, and such a clearer enlightenment could come from the comparisons between different experimental conditions (resting-state, task-induced states) and populations of subjects (healthy controls, diseased patients). Indeed, further utilizations of our proposed methodological approach should consider more heterogeneous datasets and different clinical settings. Moreover, future studies should focus on the proper selection of the most relevant networks in resting state, i.e., the ones which interact more between each other in redundant or synergistic ways. The proposed framework could also be applied to different fMRI data (e.g., task-induced states) or used to analyze multiplets where signals belonging to different organs are included, in order to assess for instance brain-heart interactions according and to investigate the role on brain activity of peripheral physiological oscillations on brain activity [29].