A Bayesian Approach to Lamb-Wave Dispersion Curve Material Identification in Composite Plates

Abstract

Guided waves are gaining increased interest in SHM, thanks to some distinct advantages. For guided-wave-based localisation strategies, information on the group velocity is required; therefore, determination of accurate dispersion curves is invaluable. However, for complex materials, the wave speed is dependent on the propagation angle. From experimental observations of dispersion curves, measured using a two-dimensional Fourier transform, a system identification procedure can be used to determine the estimated value and distribution for the governing material properties. Markov-chain Monte Carlo (MCMC) sampling can provide a way of simulating samples from these distributions, which would require solving dispersion curves many times. By using a novel Legendre polynomial expansion approach, the computational cost of dispersion curve solutions is greatly reduced, making the MCMC procedure a more practical approach In this work, a scanning laser Doppler vibrometer is used to record the propagation of Lamb waves in a carbon-fibre-composite plates, and points on the dispersion curve are extracted. These observations are then fed into the MCMC material identification procedure to provide a Bayesian approach to determining properties governing Lamb wave propagation at various angles in the plate. The distribution of parameters at each angle is discussed, including the inferred confidence in the predicted parameters.

1 Introduction

The use of ultrasonic guided waves (UGWs) for structural health monitoring (SHM) strategies [1] can offer a number of distinct advantages, such as range and sizing potential, greater sensitivity and cost effectiveness. UGWs commonly consist of two types of high-frequency stress waves: Rayleigh waves, which propagate on a surface, or Lamb waves, which propagate in ‘thin’ plates. Explanations of Rayleigh and Lamb waves are given by Worden [2] and Rose [3], however a particular characteristic of Lamb waves is their separation into symmetric and antisymmetric modes. The number of each type of wave mode present increases with increasing frequency-thickness; these are termed higher-order modes. A wave-packet is a single burst containing multiple wave modes of different frequency and shape; for Lamb waves, these will contain both types of modes. The propagation velocity of Lamb waves depends on the central frequency of the wave and will vary between the modes present; therefore a wave-packet of mixed wavelengths will spread out in space, i.e. it will disperse.

The dispersion relationship is more completely described by defining a map between the frequency and the wavenumber, which can be plotted as dispersion curves. Use of dispersion curve information is essential in guided wave-based SHM strategies, one example being to use known group velocities for damage localisation [4, 5]. In practice, the governing elastodynamic equations are numerically solved to determine these curves. For isotropic materials this can be done using a simple iterative procedure to find the phase velocity at a given frequency [3]. However, modelling guided-wave phenomena in complex materials is much more difficult, because the anisotropy results in more complicated behaviour, as well as requiring knowledge of the full stiffness tensor. For complex materials, there is no standard method of solving dispersion curves, although many are available which have distinct advantages for different uses. An approach by Solie and Auld [6] attempts to derive the equations using the partial wave technique. Traditionally, matrix formulations are also used to retrieve wave propagation characteristics for a given frequency [7].

The curves are defined by a list of material properties, the number of which can become extensive for anisotropic and/or inhomogeneous materials. It follows then, that information on the curves may allow for determination of the material properties. Previously, a method involving the use of a genetic algorithm has been presented which estimated the elastic constants of a fibre-composite plate using dispersion curves [8]; the approach generates feasible elastic constants and a distribution based on an assumed Gaussian posterior. However, there is a shortcoming in the assumption of the posterior shape, as well as the absence of cross-correlation between elastic constants. Furthermore, the genetic algorithm approach is highly computationally expensive [9].

Here, an alternative approach to dispersion curve-based material identification is presented, which utilises a probabilistic approach to simulate samples from the posterior using a Markov-Chain Monte Carlo [10] procedure. This approach allows for simulation of the true shape of the posterior, as well as to provide information on the multivariate distributions of the parameters. Previously, such an approach may not have been feasible as the solutions via dispersion curves of complex materials are computationally expensive; however, via the use of the Legendre polynomial expansion approach first shown by Lefebvre [11], it is more feasible. In this work, several numerical tricks have been implemented to speed up the Markov-Chain Monte Carlo sampling procedure, further reducing computational expense.

2 Methods

2.1 Dispersion Curve Solutions for Orthotropic Media

As mentioned earlier, the work of Lefebvre [11] is used here for determining dispersion curves in anisotropic media. For this case, an orthotropic model is used, which is described in detail by Cunfu [12] and Othmani [13], although a brief overview will be given here. In this paper, the decoupled equations which govern the shear-horizontal modes are omitted for brevity. For orthotropic materials, the generalised Hooke’s law is used to generate the governing Lamb wave equations,

$$\begin{aligned} \begin{aligned} -\frac{\omega ^2}{k^2} U_1 =&-U_1\frac{C_{11}}{\rho } + iU'_3\left( \frac{C_{13} + C_{55}}{\rho }\right) + U''_1\frac{C_{55}}{\rho } \\&+ iU_3\frac{C_{55}}{\rho }\left( \delta (q3)-\delta (q3-kh)\right) + U'_1\frac{C_{55}}{\rho }\left( \delta (q3)-\delta (q3-kh)\right) \end{aligned} \end{aligned}$$

(1a)

$$\begin{aligned} \begin{aligned} -\frac{\omega ^2}{k^2} U_3 =&-U_3\frac{C_{55}}{\rho } + iU'_1\left( \frac{C_{31} + C_{55}}{\rho }\right) + U''_3\frac{C_{33}}{\rho } \\&+ iU_1\frac{C_{13}}{\rho }\left( \delta (q3)-\delta (q3-kh)\right) + U'_3\frac{C_{55}}{\rho }\left( \delta (q3)-\delta (q3-kh)\right) \end{aligned} \end{aligned}$$

(1b)

where $q_3 = kx_3$ is the dimensionless wavenumber, the superscript ($'$) refers to the partial derivative with respect to $q_3$, and $\delta$ is the Dirac delta function.

In order to solve the decoupled wave equations, the Legendre polynomial method expands $U_i(x_3)$ into an orthonormal polynomial basis [11, 13],

$$\begin{aligned} U_i(q_3) = \sum _{m=0}^{\infty }p_m^iQ_m(q_3), \quad i=1,2,3 \qquad Q_m(q_3) = \sqrt{\frac{2m+1}{kh}}P_m\left( \frac{q_3}{kh}-1\right) \end{aligned}$$

(2)

where $p_m^i$ is the expansion coefficient and $P_m(x)$ is the Legendre polynomial expansion of order m. Theoretically, m runs from 0 to $\infty$; however, in practice, the summation over polynomials in Eq. (2) can be halted at some finite value of $m=M$, when higher-order terms become negligible. Following [13], a value of $M=4$ is used here.

To retrieve the final equations for solution, one substitutes Eq. (2) into Eq. (1), multiplies by $Q_j^*(q_3)$ and integrates over $q_3$ from 0 to kh, giving,

$$\begin{aligned} \frac{\omega ^2}{k^2}p_m^1&= -M_{jm}^{-1}\left[ A_{11}^{jm}p_m^1 + A_{13}^{jm}p_m^3\right] \end{aligned}$$

(3a)

$$\begin{aligned} \frac{\omega ^2}{k^2}p_m^3&= -M_{jm}^{-1}\left[ A_{31}^{jm}p_m^1 + A_{33}^{jm}p_m^3\right] \end{aligned}$$

(3b)

with j and m running from 0 to M, and ‘$^*$’ means the complex conjugate. The definition of the matrix elements are shown in [13].

By separating out Eq. (3) into only the coupled Lamb wave modes and decoupled SH wave mode, the final solution can be arranged as an eigenvalue problem,

$$\begin{aligned} \begin{bmatrix} A_{11}^{jm} &{} A_{13}^{jm} \\ A_{31}^{jm} &{} A_{33}^{jm} \end{bmatrix} \begin{bmatrix} p_m^1 \\ p_m^3 \end{bmatrix}&= -\frac{\omega ^2}{k^2} M_{jm} \begin{bmatrix} p_m^1 \\ p_m^3 \end{bmatrix} \end{aligned}$$

(4a)

with eigenvalues $\lambda =\text {--}c_p^2$ and corresponding eigenvectors $\{p_m^1, p_m^3\}^{\top }$. The solutions to be accepted are only those eigenmodes for which convergence is obtained as M is increased [11, 13].

2.2 Measuring $\{\hat{\omega },\hat{k}\}$

The first stage of the process here is to determine a set of measured values on the dispersion curve $\{\hat{\omega },\hat{k}\}$ of the plate in question. Experimentally, this can be obtained by first measuring the surface displacement of a wave at regularly-spaced intervals is measured to form time-distance [$t\hbox {-}x$] data. The signals at each spatial location are then normalised and the matrix passed through a two-dimensional Fourier transform (2DFT) to retrieve frequency-wavenumber [$\omega \hbox {-}k$] data [14].

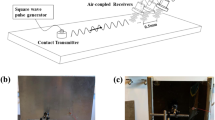
Lamb waves were initiated in a carbon-fibre reinforced polymer plate by excitation of a 20 mm diameter piezo-electric transducer (PZT), at the centre of the plate, as shown in Fig. 1a. The CFRP plate consisted of a $[90/0/90]_s$ layup, and measured 300 mm $\times$ 300 mm $\times$ 1 mm. The PZT was actuated with a 300 kHz, 5-cycle, Hanning-windowed sine wave, allowing multiple wave modes to be excited. A Polytec scanning-laser vibrometer was used to measure the out-of-plane surface displacement of the induced wave-packets on the opposite side of the plate to the PZT, with recording length 4ms and at a sampling rate of 1.024 MHz. One-dimensional wave propagation data were then extracted at two different propagation angles; 0$^\circ$ and 90$^\circ$. The [$t\hbox {-}x$] data were then passed through a 2DFT to form dispersion curve images at each angle; the results for 90$^\circ$ are shown in Fig. 1b.

Fig. 1.

(a) Diagram showing a top-down view of the experimental setup with location of PZT on the 300 mm$\times$300 mm CFRP plate and (b) the dispersion curve image data for a propagation angle of 90$^\circ$.

At a propagation angle of 90$^\circ$, the dispersion curve shows strongly the $A_0$ mode, and has a noisy representation of the $S_0$ mode visible. The [$\omega \hbox {-}k$] image data are then passed through a simple ridge-picking algorithm to select points which are on the curve; in this case, only the $A_0$ mode is considered.

2.3 Estimating Elastic Constants

Using known points on the dispersion curve a maximum-likelihood estimate can be formulated, which returns the most likely parameters, given point data [15]. In this case, the model is assumed be of the form,

$$\begin{aligned} \omega = f(k, \varTheta ) + \varepsilon \end{aligned}$$

(5)

where $\varTheta$ is a set of parameters which govern the solutions of the dispersion equation and $\varepsilon$ is white Gaussian noise. The function $f(k,\varTheta )$ is formed using the method presented above, the parameters are $\varTheta = \{C_{11},C_{13},C_{33},C_{55},\rho \}$. Given a set of observations $\mathbf {y}=\{\hat{\omega },\hat{k}\}$, the likelihood is defined as,

$$\begin{aligned} L(\mathbf {y}|\varTheta ) = \prod _{i=1}^n \frac{1}{\sqrt{2\pi \sigma ^2}} \exp \left( -\frac{\left( \hat{\omega }_i-f(\hat{k}_i,\varTheta )\right) ^2}{2\sigma ^2}\right) \end{aligned}$$

(6)

where n is the number of observations of the dispersion curve. Maximising $L(\mathbf {y}|\varTheta )$ provides an estimate of the most likely elastic constants; however, it is also possible to retrieve information on their distribution.

2.4 Sampling over the Posterior Distribution

Markov chain Monte-Carlo (MCMC) sampling is a computational sampling method [10, 16] which allows one to characterise the distribution of a set of parameters without knowing the parameter properties. In traditional Monte-Carlo sampling, a distribution is formed by random sampling from the posterior distribution. As no basis is provided for the next sample made, extensive sampling is required to form an accurate model of the posterior distribution. In MCMC sampling, the next sample is chosen based on the posterior probability, so the chain will converge towards its stationary distribution.

A detailed description is given by Barber [17], although a brief overview will be given here. MCMC is an iterative sampling procedure where the subsequent samples depend on assessing their probability with respect to the previous sample. As the likelihood includes the noise variance term $\sigma$, the parameter vector is extended to include this, $\theta = \{\varTheta ,\sigma \}$. The aim is to find a distribution over the parameters $\theta$ by sampling them based on their likelihood given a set of observations $\mathbf {y}$. At each step of the iteration an acceptance ratio is defined as,

$$\begin{aligned} \hat{\alpha } = \frac{p(\mathbf {y}|\theta ')p(\theta ')}{p(\mathbf {y}|\theta _k)p(\theta _k)} \end{aligned}$$

(7)

where $\theta '$ is the current estimate and $\theta _k$ is the previous estimate, $p(\theta )$ is the prior distribution of $\theta$, and $p(\mathbf {y}|\theta )$ is the likelihood as defined in Eq. (6). The current estimate is accepted if $\hat{\alpha } > 1$.

In addition to the likelihood, the priors must be defined to embed any prior belief of the distribution of the parameters. This definition can be done using any previous knowledge of the system; in this case, the density of the plate was provided but no other material properties. Thus, a tight prior can be given on $\rho$, and then priors on other values are defined based on reasonable values for the material.

3 Results

The results of 5000 iterations of the sampling procedure for propagation angles of 0$^\circ$ and 90$^\circ$ are shown in Figs. 2 and 3 respectively. From the figures, the posterior distributions of the parameters can be seen as both univariate and bivariate distributions. In both propagation angles, there is evidence of correlation between material parameters, whereas the distribution of the noise parameter appears to converge to a univariate distribution. This result is anticipated, as the elastic properties which form the stiffness matrix are described by a series of inseparable equations. For 0$^\circ$, there appears to be a strong correlation between $C_{33}$ and both $C_{13}$ and $C_{11}$, as well as a very strong correlation between the values of $C_{55}$ and $\rho$.

Fig. 2.

Results of the parameter identification procedure for the propagation angle of 0$^\circ$. Figures along the diagonal show the histogram of the samples for each parameter. Figures in the upper right triangle show a scatter plot of correlation between two parameters. Figures in the lower left triangle show a bivariate kernel density estimate of the cross-correlation between parameters, where lighter colours represent a larger value of the density.

Another observation from these plots is the pronounced ‘edge’ on the scatter correlation plots between $C_{11}$ and $C_{33}$ with both $C_{55}$ and $\rho$. As a condition of the solution to the dispersion curve equations is that $\lambda <0$, any solutions where this is the case are rejected. The edge may indicate a region of forbidden parameter combinations which cannot exist given a real elastic material.

Fig. 3.

Results of the parameter identification procedure for the propagation angle of 90$^\circ$. Figures along the diagonal show the histogram of the samples for each parameter. Figures in the upper right triangle show a scatter plot of cross-correlation between two parameters. Figures in the lower left triangle show a bivariate kernel density estimate of the cross-correlation between parameters, where lighter colours represent a larger value of the density.

In comparison to the results for the 0$^\circ$ propagation angle, there are some notable differences in the posterior distributions for the propagation angle of 90$^\circ$. Firstly, the distribution of $C_{11}$ converges to a statistical mode of lower value and $C_{55}$ converges to that of a higher value – indicating the elastic constants are lower and higher respectively. This would indicate that, even with the carbon-fibre weave material, the energy of the antisymmetric mode is dominated by a particular fibre orientation; otherwise it would be expected that for both fibre orientations the posteriors would remain similar. Furthermore, the correlation between $C_{55}$ and $\rho$ appears to be much weaker than at a propagation angle of 0$^\circ$, and instead there is a strong correlation between $C_{11}$ and $\rho$.

For each of the parameters, a kernel density estimate of the posterior distribution was applied to the samples from the posterior distributions for each parameter and for both angles, the results of which are shown in Table 1. The mean values of $C_{33}$, $\rho$ and $\sigma$ are similar for both propagation angles, whereas the mean values for $C_{11}$, $C_{13}$ and $C_{55}$ appear to change depending on the propagation angle. The largest of these changes is that of the value of $C_{55}$, however, this could be explained by looking at the distribution of curves in Fig. 4. As there are additional points returned from the ridge-picking algorithm in the results for the propagation angle of 0$^\circ$, the likelihood calculation is at a maximum when the $S_0$ curve has a shape which covers these points. The $C_{55}$ elastic constant effects the $S_0$ curve past the ‘elbow’ [18] and so these additional measured points will tighten the posterior distribution for $C_{55}$.

Using the parameters at each sample point, a distribution of the dispersion curves was also produced, and is shown in Fig. 4, along with the observation points taken from the [$\omega \hbox {-}k$] image data. An initial observation is of the dissimilarity of the $S_0$ mode curves and their representation in the image data. In both cases, wavenumber is calculated to be higher for all samples drawn. For dispersion curves of unidirectional fibre-composite materials, the $A_0$ mode is mostly sensitive to the $C_{11}$, $C_{55}$ at 0$^\circ$, and additionally the $C_{13}$ and $C_{33}$ parameters at 90$^\circ$ [18]. As the distributions are only sampled based on observations of the $A_0$ mode, it will only be influenced by those to which the curves are sensitive.

Table 1. Calculated mean (first statistical mode) and standard deviation (STD) taken from fitting a kernel density estimate to the samples from the posterior for each parameter.

Fig. 4.

Distribution of generated curves for each sample taken for propagation angles of (a) 0$^\circ$ and (b) 90$^\circ$. The blue curves show the distribution of the $A_0$ mode and red curves show the distribution of the $S_0$ mode. The curves are overlaid on the image data taken from the 2DFT and the red dots indicate the points taken from the ridge selection algorithm which were used in the procedure as $\{\hat{\omega },\hat{k}\}$.

For all samples drawn, the model for the dispersion curve of the $A_0$ is very accurate and lies well within the measured observation points. An interesting note relates to the additional observation points at $\omega > 2.5$ Mrad/s for the propagation angle of 0$^\circ$. These additional points are likely the cause of the tighter distribution of curves for this propagation angles, and is likely to be a result of a clearer dispersion curve on the image data.

In this work, the dispersion curves are solved using an orthotropic model. For the objectives of the work here, the model provides accurate results based on comparison to the image data provided. It is important to note the restriction of the curves to the bandwidth available in the observations.

4 Conclusions and Further Work

A method has been presented here for determining the posterior distributions of elastic properties which govern dispersion curves for complex materials. The samples drawn from the procedure also give an indication of the joint distributions of the parameters and how they are correlated. The posterior distribution of the dispersion curves also shows that the method provides accurate modelling in the context of key properties for SHM strategies – such as group velocity. With implementation of the method, consideration of the bandwidth of the observed values is important. Although shown here in the context of determining dispersion curves for the fundamental Lamb wave modes, the method is readily expandable to become a full system-identification procedure. Further work will be done to expand this, by inclusion of the $S_0$ mode as well as SH modes.