Keywords

4.1 Introduction

Event-based imaging, utilizing silicon retinas, has been a developing field of study for approximately 35 years. The pioneers of this emergent imaging technology were Misha Mahowald and Carver Mead [1, 2]. For many years, the use of event-driven retina cameras was limited to experimental study and development in a relatively few research laboratories. However, event-based vision sensors are now commercially available for industrial use [3].

The use of silicon retina cameras/sensors in the field of structural dynamics is both promising and attractive because of the way data is captured and generated. These types of sensors generate data asynchronously with low latency, high dynamic range, high temporal resolution, high pixel bandwidth, and low power consumption [1]. Additionally, when compared to traditional high-speed video cameras, work completed at Los Alamos National Laboratory (LANL) has indicated the potential for silicon retina cameras in the field of structural dynamics [4]. Further, high-speed video cameras suffer from relatively slow synchronous frame rates and shutter speeds and are computationally inefficient as compared to silicon retinas. When compared to other sensor technologies, such as strain gauges and accelerometers, event-based cameras are also attractive because they can provide noncontact vibrational analysis of a feature or structure [3, 5,6,7,8,9,10].

When paired with a neuromorphic processor, silicon retinas become the silicon analogue of the human eye, neural pathway, and the occipital lobe of the brain. Just as human vision operates with spiking neurons, event-based silicon retinas utilize a spiking neural network (SNN) and neuromorphic algorithms and computing to generate visual data. As is the case with the human eye and brain, event-driven imagers and spiking neural networks do not process and generate data synchronously based on time series. This presents a problem since time-series data is typically used for structural analysis [11,12,13].

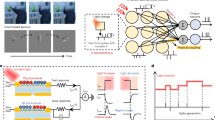
Our overall project goal is to convert silicon retina data into time-series data and find the frequencies and directions of traveling waves using the Legendre memory unit and beamforming through spike-based computing. The Legendre memory unit is used to find the frequencies of the wave pool, and beamforming is used to find the direction.

We start with raw data of the motion of a wave pool, and this data is recorded through a silicon retina. Using neuromorphic spike-based processing and a python extension called Nengo, we can use the Legendre memory unit to efficiently represent data, and then implement beamforming to understand the frequencies and angles of traveling waves. The Legendre memory unit is used in performing two important integral transformations, definite integration and short-time Fourier transformation, on event-based imagery. We demonstrate a phased array running on neuromorphic hardware analyzing acoustic data, such as video of a water tank.

4.2 Background

The Legendre memory unit (LMU) is composed of a linear layer and a nonlinear layer. The linear layer is a linear time-invariant (LTI) system of the form:

$$ \theta \dot{m}(t)= Am(t)+ Bu(t) $$
(4.1)

and can optimally reconstruct a delayed input signal with an output matrix:

$$ u\left(t-{\theta}^{\prime}\right)\approx C\left({\theta}^{\prime}\right)m(t) $$
(4.2)

where:

$$ A={\left[a\right]}_{ij}\in {R}^{d\times d},\left\{\begin{array}{c}{a}_{ij}=\left(2i+1\right),\mathrm{if}\ i<j\ {\left(-1\right)}^{i-j-1}\\ {}-1,\kern0.5em \mathrm{if}\ j\ge i\end{array}\right. $$
(4.3)
$$ B={\left[b\right]}_i\in {R}^{d\times 1},{b}_i=\left(2i+1\right){\left(-1\right)}^i $$
(4.4)
$$ C\left({\theta}^{\prime}\right)={\left[c\right]}_i\in {R}^{d\times 1},{c}_i={P}_i\left(\frac{\theta^{\prime }}{\theta}\right) $$
(4.5)
$$ {P}_i\left(\frac{\theta^{\prime }}{\theta}\right)={\left(-1\right)}^i{\sum}_{j=0}^i\left(\frac{i}{j}\right)\left(\frac{i+j}{j}\right){\left(-r\right)}^j $$
(4.6)

where i, j ∈ [0, d − 1] and \( {P}_i\left(\frac{\theta^{\prime }}{\theta}\right) \) are the shifted Legendre polynomials.

4.3 LMU Definite Integration and Fourier Transform

Voelker briefly mentions that integral transformations over the rolling window history are possible [14]. We provide examples of such transformations on the input signal by replacing the output matrix C with a transformation of the C matrix. Two examples of this are definite integration and the Fourier transform. The definite integration can be thought of as a scaled partial summation of the original output:

$$ {\int}_{t-\uptheta}^tu\left(\sigma \right) d\sigma \approx \left({\int}_0^{\theta }C\left({\theta}^{\prime}\right)d{\theta}^{\prime}\right)m(t) $$
(4.7)

where t is time, θ is the time shift, u(σ) is used to integrate by substitution, and m(t) is the state of the LMU as detailed in Eq. (4.1).

Fig. 4.1
figure 1

(Left) One frame from silicon retina footage of a piece of plastic dropped into water and (Right) it’s 2D Fourier transform. Red dashed line indicates the position of the 12 equidistant pixels used to form the antenna. X and Y coordinates represent pixel numbers

Full size image

The Fourier transform is simply the FFT matrix multiplied by the measurement matrix C.

4.4 LMU Beamforming

After constructing the two integral transformations, we provided an application of these two data processing techniques: an LMU beamformer. The beamforming technique we used was the “delay and sum” since the LMU is particularly effective at delaying signals. We selected 12 pixels, which serve as virtual receivers, which were aligned vertically, equidistantly spaced apart. The signals were each delayed according to Eq. 4.8:

$$ {\tau}_i=\frac{y_i\cos \left(\cos\ \left(\theta \right)\right)}{c}-\min \left(\frac{y_i\cos \left(\cos\ \left(\theta \right)\right)\ }{c}\right), $$
(4.8)

where y i is the i th pixel’s position, θ is the desired orientation of the beam, c is the speed of sound in pixels per second, and τ i is the delay imposed on the i th pixel’s signal. The delay of each signal was implemented using 12 LMUs (Fig. 4.1).

We want to perform spectral analysis on the traveling waves; the outputs corresponding to different orientations of the beams are each passed through an LMU spectrogram. Since we’re interested in the dominant traveling wave, we compute the magnitude of the signal received for each orientation. The magnitude of the signal is plotted on Fig. 4.2 (left) and was computed as the square of the magnitude. The spectrogram of the maximal traveling wave is plotted on Fig. 4.2 (right).

Fig. 4.2
figure 2

(Left) output of phased array on data from Fig. 4.1, swept over angles ranging from 0 to 2π. (Right) spectrogram over angle of maximum signal

Full size image

4.5 Conclusion

We demonstrate the Legendre memory unit’s ability in performing two important integral transformations, definite integration and short-time Fourier transformation, on event-based imagery. We demonstrate a phased array running on neuromorphic hardware analyzing acoustic data, such as video of a water tank. For future work, a projected application is that the silicon retina data and the Legendre memory unit can enable the development of a prototype neuromorphic computing framework suitable for online (real-time) data processing.