Prediction of Footbridge Vibrations and Their Dependence on Pedestrian Loads

Abstract

Prediction of structural vibrations due to vertical loads generated by pedestrians is an assignment that many engineers involved with footbridge design have encountered. Often, the problem matter is not ultimate limit-state-requirements, but concern is on serviceability-limit-state requirements in the form of potential excessive structural vibrations. The nature of human locomotion dictates that the action of pedestrians on footbridges is random. This also has the effect that the footbridge vibrational response is random and potentially depends on a set of walking parameters (pacing speed, load amplifications factors, pedestrian weight, etc.) and the stochastic nature of these parameters. The paper will address issues of predicting footbridge vibrations in this context, taking offset in artificial footbridges. Monte Carlo simulations and Newmark time integration will be employed for determining footbridge vibrations.

FormalPara Nomenclature

a	Bridge acceleration	f 1	Bridge fundamental frequency	f s	Step frequency
i	Integer	m 1	Bridge modal mass	l s	Step length
v	Pacing speed	t	Time	F	Walking load
L	Bridge length	Q	Modal load	W	Weight of pedestrian
α	Dynamic load factor	ζ 1	Bridge damping ratio	μ	Mean value
σ	Standard deviation	$\theta$	Phase	$\Phi$	Mode shape

16.1 Introduction

It is well known that footbridges can be flexible and that this can be of concern. An example of this is the Millennium Bridge vibrations [1] that occurred as a result of human locomotion.

The bridge turned out unfit for its intended use. The problem was not the ultimate-limit-state but the serviceability-limit-state. Persons passing the bridge felt uncomfortable, and it was due to the actions of pedestrians generating forces onto the bridge bringing it into vibration. The general problem was resonant excitation.

The present paper also addresses vibrations generated by pedestrians based on the modelling of walking loads. A lot of works done previously have addressed modelling walking loads, for instance [2,3,4]. In these works, walking loads were modelled in a deterministic manner.

However, by nature, human locomotion is stochastic. This is recognised in [5,6,7,8,9,10] either by modelling the walking parameters as random variables or by setting up a stochastic framework for computing footbridge vibrations.

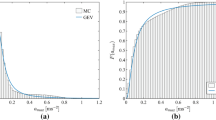
In this paper the probabilistic/stochastic approach is adopted. Since walking parameters will be modelled as random variables, also the bridge acceleration response will be stochastic. The bridge response in focus in the paper will be the 95% quantile of midspan bridge accelerations.

This property (a ₉₅) will be estimated using Newmark time integration combined with the use of Monte Carlo simulation methods for a set of artificial single-span pin-supported bridges.

The aim of the paper is on examining how a selected subset of possible load model assumptions influences estimates of a ₉₅, basically to test how sensitive the outcome of calculations is to different load model assumptions.

Section 16.2 outlines the main structure of the load model and assumptions made in terms of the stochastic nature of walking parameters. Section 16.3 presents two different studies exploring how sensitive a ₉₅ is to different load model assumptions. Section 16.4 summarises the conclusions.

16.2 Modelling of Walking Loads

The modelling of walking loads is based on Eq. (16.1).

$$ Q(t)=\Phi (t)F(t) $$

(16.1)

In this equation, Q(t) represents the modal load, and F(t) represents the vertical force generated by the pedestrian. Ф(t) is the mode shape function assumed to take on values calculated from Eq. (16.2).

$$ \Phi (t)=\sin \left(\pi vt/L\right) $$

(16.2)

Hence, it is assumed that it is the first bending mode that governs the response.

In Eq. (16.2), v is the pacing speed of the pedestrian, calculated from Eq. (16.3).

$$ v={f}_s{l}_s $$

(16.3)

In this equation, f _s is the step frequency, and l _s is the step length of the pedestrian.

These two parameters will be modelled as random variables with the parameters shown in Table 16.1. Gaussian assumptions are made for the parameters f _s and l _s.

Table 16.1 Mean values (μ) and standard deviations (σ)

In the table, also W is introduced, and it represents the static weight of the pedestrian. As can be seen, this property is handled as a deterministic property.

As for the load F(t), it is modelled in the way described by Eqs. (16.4, 16.5, and 16.6).

$$ F(t)=\sum_{i=1}^5{F}_i(t)+\sum_{i=1}^5{F}_i^S(t)\vspace*{-10pt} $$

(16.4)

$$ {F}_i(t)=W{\alpha}_i\cos \left(2\pi i{f}_st+{\varphi}_i\right)\vspace*{-10pt} $$

(16.5)

$$ {F}_i^S(t)=W{\alpha}_i^S\cos \left(\pi \left(2i-1\right){f}_st+{\varphi}_{i+5}\right) $$

(16.6)

The load model was first introduced in [10]. In its basic form, it assumes five main harmonics (entering by Eq. (16.5)) and five subharmonics (entering by Eq. (16.6)). The model assumes no leakage of energy to other frequencies outside the excitation frequencies.

As for the dynamic load factors, α _i, they are modelled as random variables and assumed to follow a Gaussian distribution.

For the first harmonic, α ₁, its mean value, μ, and standard variation, σ, are calculated from Eq. (16.7).

$$ \mu =-0.2649{f}_S^3+1.3206{f}_S^2-1.7597{f}_S+0.7613;\kern0.75em \sigma =0.16\mu $$

(16.7)

Table 16.2 defines the assumptions made for the remaining main dynamic load factors.

Table 16.2 Mean values (μ) and standard deviations (σ) [7, 9]

The subharmonic dynamic load factors ${\alpha}_i^S$ (in Eq. 16.6) are calculated from the main harmonic load factor, α ₁, according to the procedure outlined in [9], which also outlines procedures for determining the phases in Eqs. (16.5 and 16.6).

16.3 Studies of This Paper

Having defined assumptions as regards the load generated by a single pedestrian, it is possible to generate the adjoining load-time history and to compute the maximum vertical bridge acceleration response, a, that occurs at bridge midspan, while a pedestrian crosses the bridge. This was accomplished using Newmark time integration, and Monte Carlo simulations were employed for establishing a statistical representation of bridge vibration response. For each of the studies of this paper, 100,000 bridge crossings by a single pedestrian were simulated.

From the statistical basis hereby obtained, the bridge acceleration quantile a ₉₅ was extracted. This quantile is believed to be a reasonable parameter to describe the vibrational performance of a footbridge.

The footbridges considered in the studies of this paper are artificial SDOF pin-supported bridges all having a fundamental frequency (in vertical bending) in the immediate vicinity of the mean value of the step frequency assumed for the pedestrians passing the bridge.

The modal properties of the bridges will be outlined for each of the studies presented below. The studies will have focus on the fact that the engineer in charge of computations of bridge response will have different options available for his calculations (decisions to be made). Hence, the general idea is to compare values of a ₉₅ computed on different assumptions in terms of modelling walking loads.

16.3.1 Impact of Decisions Related to the Choice of Load Model

Assumed for this study is a SDOF-bridge with the modal characteristics defined in Table 16.3.

Table 16.3 Modal properties of bridge and bridge length (L)

There are other proposals in literature as to how to model F(t) than the model defined by Eqs. (16.5 and 16.6).

An alternative, for example, would be to assume the walking load model proposed in [9].

In that model, Eqs. (16.8 and 16.9) are to substitute Eqs. (16.5 and 16.6).

$$ {F}_i(t)={W\alpha}_i\sum_{{\overline{f}}_j=i-0.25}^{i+0.25}{\overline{\alpha}}_i\left({\overline{f}}_j\right)\cos \left(2\pi {\overline{f}}_j{f}_st+\theta \left({\overline{f}}_j\right)\right) $$

(16.8)

$$ {F}_i^S(t)={W\alpha}_i^S\sum_{{\overline{f}}_j^S=i-0.75}^{i-0.25}{\overline{\alpha}}_i^S\left({\overline{f}}_j^S\right)\cos \left(2\pi {\overline{f}}_j^S{f}_st+\theta \left({\overline{f}}_j^S\right)\right) $$

(16.9)

For a full description of the parameters in Eqs. (16.8 and 16.9), reference is made to [9].

This model also (as the model introduced in Sect. 16.2) consists of main load harmonics (Eq. (16.8)) and subharmonics (Eq. (16.9)). The difference is that this model accounts for a leakage of energy in the sense that a full periodic excitation is not assumed.

For both load model assumptions values of a ₉₅ were computed, and results are shown in Table 16.4.

Table 16.4 Computed values of a ₉₅

It appears that the model that does not account for leakage of energy results in the higher value of a ₉₅. This is as expected as when leakage is assumed to occur, it will be accompanied with less energy exciting at the fundamental frequency of the bridge.

The difference between the two results is only 3%. So for this particular scenario, it may not be worthwhile employing the quite advanced load model that accounts for leakage.

16.3.2 Impact of Decisions Related to Modelling the Load Amplification Factor

Assumed for this study is a SDOF-bridge with the modal characteristics defined in Table 16.5.

Table 16.5 Modal properties of bridge and bridge length (L)

Again, it is a bridge with a fundamental frequency in the immediate vicinity of the mean value assumed for the step frequency.

For this study, the load model outlined in Sect. 16.2 was employed. For simplicity only the first main harmonic was considered.

Basically, there are different ways in which the dynamic load factor associated with first load harmonic can be derived.

In the more advanced approach, it is considered that for every pedestrian that crosses the bridge, different values of α ₁will come up for the calculation of bridge vibration, as this parameter (α ₁) is a function of step frequency (see Eq. (16.7)), and as the step frequency is modelled as a random variable, the value of α ₁cannot be the same for every pedestrian.

However, a study was made in which the value of α ₁was picked from Eq. (16.7) by entering the mean value for the step frequency assumed for the entire population of pedestrians crossing the bridge for every pedestrian.

It turned out that the difference in the computed value of a ₉₅ differed by less than 2%.

16.4 Conclusion and Discussion

The paper has had focus on a subset of the decisions that the engineer in charge of calculations of the bridge acceleration quantile a ₉₅ (the acceleration level exceeded in 5% of the pedestrian crossings) need to make.

The decisions related to how to model the walking loads of the pedestrians assumed to cross the bridge one by one.

Two different load models were examined, and a simplified approach for determining dynamic load factors versus a more advanced approach was also studied.

In both cases (in both studies), it turned out that value of a ₉₅ was only slightly sensitive to the approach chosen for modelling the action of walking.

This suggests that it might not always be necessary to employ the most advanced load models (although they replicate the load mechanism better), which is useful to know.

This conclusion is drawn from studying only SDOF pin-supported footbridges with fundamental frequencies in the immediate vicinity of the mean value for the step frequency of the population of pedestrians. It would be interesting to study whether this is also valid for bridges with other bridge frequencies.