Keywords

Low-yield-point steels are widely applied in energy dissipation members. Their cyclic behaviour under earthquake loadings has significant influence on the structural performance. Therefore, it is necessary to develop cyclic plasticity model of such steels for accurate evaluation of their energy dissipation capacities. Nowadays, there have been lots of experimental studies on cyclic responses of low-yield-point steels [1,2,3,4,5,6], but how to model their stress-strain responses accurately still remains a practical problem. This paper is mainly devoted to the verification of a cyclic plasticity model developed by the author for mild steels [7, 8] in prediction of stress-strain relations of low-yield-point steels with nominal yield strength lower than 235 MPa, which are much different from conventional mild steels in that they generally have much lower yield-to-tensile strength ratios and thus, more significant strain hardening beyond yield plateau.

1 Review of Cyclic Plasticity Model [7, 8]

1.1 General Equations

The total strain rate tensor is decomposed into elastic and plastic strain rate components as

$$ \dot{\varepsilon } = \dot{\varepsilon }^{{\text{e}}} + \dot{\varepsilon }^{{\text{p}}} $$
(1)

where the elastic strain rate is associated with the stress rate by Hooke’s law. The plastic behaviour is characterized by von Mises yield surface

$$ f = \overline{\sigma } - R = \sqrt {\frac{3}{2}\left( {{\varvec{s}} - {\varvec{\alpha}}} \right):\left( {{\varvec{s}} - {\varvec{\alpha}}} \right)} - R = 0 $$
(2)

where \(\overline{\sigma }\) is the effective von Mises stress and R is the radius of yield surface; \({\varvec{\alpha}}\) is the back stress tensor and \({\varvec{s}}\) is deviatoric stress tensor which is defined as

$$ {\varvec{s}} = {\varvec{\sigma}} - \frac{1}{3}{\text{tr}}\left( {\varvec{\sigma}} \right){\mathbf{1}} $$
(3)

where “tr” indicates the trace operator and \({\varvec{\sigma}}\) is the stress tensor. Associated flow rule is used to determine the plastic strain rate tensor as

$$ \dot{\user2{\varepsilon }}^{{\text{p}}} = \dot{\lambda }\frac{\partial f}{{\partial {\varvec{\sigma}}}} = \frac{3}{2}{\varvec{n}}\dot{\overline{\varepsilon }}^{{\text{p}}} = \frac{3}{2}\frac{{{\varvec{s}} - {\varvec{\alpha}}}}{{\overline{\sigma }}}\dot{\overline{\varepsilon }}^{{\text{p}}} $$
(4)

where n is the flow direction normal to the yield surface, and \(\dot{\overline{\varepsilon }}^{{\text{p}}}\) denotes the equivalent plastic strain rate, which is defined as

$$ \dot{\overline{\varepsilon }}^{{\text{p}}} = \sqrt {\frac{2}{3}\dot{\user2{\varepsilon }}^{{\text{p}}} :\dot{\user2{\varepsilon }}^{{\text{p}}} } $$
(5)

1.2 Hardening Rules

Classical nonlinear isotropic and kinematic hardening rules are used. Isotropic hardening is described by

$$ \dot{R} = \sum\limits_{j} {\dot{R}_{j} } $$
(6)
$$ \dot{R}_{j} = b_{j} \left( {Q_{j} - R_{j} } \right)\dot{\overline{\varepsilon }}^{{\text{p}}} $$
(7)

where \(\dot{R}\) is the total change rate of the radius of yield surface and it is decomposed into multiple components \(\dot{R}_{j}\) each with independent hardening parameters \(b_{j}\) and \(Q_{j}\). Note that \(Q_{j}\) represents the saturated value of \(R_{j}\) and a positive value of that indicates isotropic hardening, and softening otherwise, while \(b_{j}\) represents the rate of evolution.

Kinematic hardening is described by the evolution law proposed by Armstrong and Frederick [9] in the form

$$ \dot{\user2{\alpha }} = \sum\limits_{j} {\dot{\user2{\alpha }}_{j} } $$
(8)
$$ \dot{\user2{\alpha }}_{j} = \frac{2}{3}C_{j} \dot{\user2{\varepsilon }}^{{\text{p}}} - \gamma_{j} {\varvec{\alpha}}_{j} \dot{\overline{\varepsilon }}^{{\text{p}}} $$
(9)

where \(\dot{\user2{\alpha }}\) is the total backstress rate and it is also decomposed into multiple tensor components \(\dot{\user2{\alpha }}_{j}\) each with independent hardening parameters \(C_{j}\) and \(\gamma_{j}\).

A memory surface is defined in plastic strain space as

$$ g = \sqrt {\frac{2}{3}\left( {{\varvec{\varepsilon}}^{{\text{p}}} - {\varvec{\xi}}} \right):\left( {{\varvec{\varepsilon}}^{{\text{p}}} - {\varvec{\xi}}} \right)} - r = 0 $$
(10)

where

$$ \dot{\user2{\xi }} = \left( {1 - c} \right)H\left( g \right)\left\langle {{\varvec{m}}:\frac{2}{3}\dot{\user2{\varepsilon }}^{{\text{p}}} } \right\rangle {\varvec{m}} $$
(11)
$$ \dot{r} = cH\left( g \right)\left\langle {{\varvec{n}}:{\varvec{m}}} \right\rangle \dot{\overline{\varepsilon }}^{{\text{p}}} $$
(12)

where r is the radius of the memory surface; c is a scalar material parameter which determines the rate of expansion of the memory surface; H(g) is Heaviside function, i.e. H(g) = 1 if g = 0 and H(g) = 0 if g < 0; < > denotes the Macaulay brackets, i.e. <a> = a if a > 0 and <a> = 0 if a < 0; m is the direction normal to the memory surface:

$$ {\varvec{m}} = \frac{{{\varvec{\varepsilon}}^{{\text{p}}} - {\varvec{\xi}}}}{r} $$
(13)

Isotropic softening or hardening is deactivated when the plastic strain state lies inside the memory surface. Thus, two sets of parameters cs and cl are used for short-range and long-range hardening, respectively.

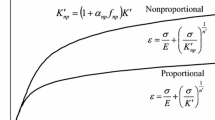
Another important parameter \(\overline{\varepsilon }_{{{\text{st}}}}^{{\text{p}}}\) is also included to determine whether current stress state belong to the plateau region or hardening region. The following criterion proposed by Ucak and Tsopelas [10] is assumed

$$ \begin{array}{*{20}c} {{\text{if }}r \le \overline{\varepsilon }_{{{\text{st}}}}^{{\text{p}}} {\text{ or }}\overline{\varepsilon }^{{\text{p}}} \le \varepsilon_{{{\text{st}}}}^{{\text{p}}} \to {\text{plateau region}}} \\ {{\text{if }}r > \overline{\varepsilon }_{{{\text{st}}}}^{{\text{p}}} {\text{ and }}\overline{\varepsilon }^{{\text{p}}} > \varepsilon_{{{\text{st}}}}^{{\text{p}}} \to {\text{hardening region}}} \\ \end{array} $$
(14)

1.3 Parameter Calibration

A concise calibration procedure for isotropic and kinematic hardening parameters by monotonic true stress-plastic strain curve is established. The engineering stress (s)-strain (e) relation should be transformed into a true relation by

$$ \varepsilon = \ln \left( {1 + e} \right) $$
(15)
$$ \sigma = \left( {1 + e} \right)s $$
(16)

Then elastic modulus E and yield stress \(\sigma_{{\text{y}}}\) can be directly determined. Since necking initiates at peak load, the true stress and plastic strain can be computed from nominal ones by a weighted average method by Jia and Kuwamura [11], by assuming that the true stress is linearly corelated with the true strain after the ultimate true stress \(\sigma_{{\text{u}}}\). The linear hardening modulus with respect to the plastic strain is

$$ {{H = w\sigma_{{\text{u}}} } \mathord{\left/ {\vphantom {{H = w\sigma_{{\text{u}}} } {\left( {1 - \frac{{w\sigma_{{\text{u}}} }}{E}} \right)}}} \right. \kern-\nulldelimiterspace} {\left( {1 - \frac{{w\sigma_{{\text{u}}} }}{E}} \right)}} $$
(17)

where w is a factor calibrated based on the descending part of nominal stress-strain curve.

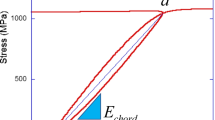
The derived monotonic true stress-plastic strain curve by the above procedure represents the upper bound of elastic range. However, the lower bound of elastic range is generally unknown. Thus, a critical assumption is made that the reversal yield stress under moderate strain amplitudes is the same, which means the yield surface saturates after initial contraction in size, as shown in Fig. 1. When the plastic strain exceeds \(\varepsilon_{{\text{u}}}^{{\text{p}}}\), the lower bound is parallel to the upper true stress-plastic strain bound, which means the yield surface saturates after subsequent expansion in size and translates only. Based on such an assumption, the initial contraction of the yield surface is described by using a short-range isotropic softening component, whose saturation \(Q^{s}\)(<0) and rate parameter \(b^{s}\) should be calibrated by the cyclic stress-strain relations.

To ensure the consistency of positive hardening modulus, two short-range nonlinear backstress components \(\alpha_{1}^{s}\) and \(\alpha_{2}^{s}\) evolve along with the above isotropic softening component with equivalent saturation and some other empirical relations

$$ - Q^{s} = \sum\limits_{j = 1}^{2} {\frac{{C_{j}^{s} }}{{\gamma_{j}^{s} }}} \quad {\text{and}}\quad \frac{{C_{1}^{s} }}{{\gamma_{1}^{s} }}:\frac{{C_{2}^{s} }}{{\gamma_{2}^{s} }} = 1:2\quad {\text{and}}\quad \gamma_{1}^{s} = 10\gamma_{2}^{s} \quad {\text{and}}\quad \gamma_{2}^{s} = b^{s} $$
(18)

The linear hardening modulus at final stage makes it natural to build a long-range linear backstress component \(\alpha_{2}^{l}\) with hardening parameters

$$ C_{2}^{l} = H{\text{ and }}\gamma_{2}^{l} = {0} $$
(19)

Thus, the rest hardening components, including a long-range backstress \(\alpha_{1}^{l}\) and an isotropic hardening component, can be derived by the geometric relations in Fig. 1. Their parameters satisfy

$$ \frac{{C_{1}^{l} }}{{\gamma_{1}^{l} }} = \frac{{\sigma_{{\text{u}}} - \sigma_{{\text{y}}} }}{2} - H\left( {\varepsilon_{{\text{u}}}^{{\text{p}}} - \varepsilon_{{{\text{st}}}}^{{\text{p}}} } \right) $$
(20)
$$ Q^{l} = \frac{{\sigma_{{\text{u}}} - \sigma_{{\text{y}}} }}{2} $$
(21)

The rate parameters \(\gamma_{1}^{l}\) and \(b^{l}\) are then calibrated to fit the monotonic stress-strain curve shape.

Fig. 1.
figure 1

Decomposition of hardening components.

Full size image

2 Comparison with Experimental Results

In order to calibrate and validate the cyclic plasticity model for low-yield-point steels, a systematic experimental investigation by Shi et al. [5] is referred to. In their study, coupon specimens made of LY100, LY160 and LY225 low-yield-point steels produced in China were subjected to monotonic tension and 12 different cyclic loadings, including various constant-amplitude, variable increasing- and decreasing-amplitude as well as some random histories. Based on the stress-strain database obtained by Shi et al. [5] and using the calibration method illustrated above, the material parameters of those LY100, LY160 and LY225 steels were determined as shown in Table 1. Comparison between experimental and modelling results are then shown in Fig. 2 for LY160 steel under 6 representative cyclic loadings, and in Fig. 3 and Fig. 4 for LY100 and LY225 steels, respectively, under a representative increasing-amplitude and a representative constant-amplitude cyclic loading. Not all the results of 12 cyclic loadings are presented to save space. It is clear that the sudden initial yield drop phenomenon is not considered and thus not captured in the modelling, but the plateau response following that is simulated well. The stress amplitudes are well captured, but the cyclic stress evolution is underestimated at relatively large-amplitude cycles. Generally, close agreement is obtained and the accuracy of the cyclic plasticity model in terms of application in steel structural engineering is evidenced.

Table 1. Calibrated parameters.
Full size table
Fig. 2.
figure 2

Stress-strain responses of LY160 steel.

Full size image
Fig. 3.
figure 3

Stress-strain responses of LY100 steel.

Full size image
Fig. 4.
figure 4

Stress-strain responses of LY225 steel.

Full size image

3 Conclusions

Cyclic plasticity models developed previously by the author for mild steels is used to model stress-strain responses of low-yield-point steels under monotonic and various cyclic loadings. The cyclic plasticity model is validated against the experimental responses and can be used further for seismic or dynamic analysis of steel structures using those steels.

The author has developed Abaqus UMAT subroutines for the cyclic plasticity model that can be employed in steel structural analysis. Details can be found in this repository: https://github.com/hfx07/upm.