Abstract
In Descartes we came to know a radical critic of contemporary rational thinking. With Gottfried Wilhelm Leibniz (1646–1716) we now turn to an equally radical diplomat who endeavoured to unite the world’s antagonisms.
Access provided by Autonomous University of Puebla. Download chapter PDF
From Two to Infinity: Leibniz’ Conception of the World
In Descartes we came to know a radical critic of contemporary rational thinking. With Gottfried Wilhelm Leibniz (1646–1716) we now turn to an equally radical diplomat who endeavoured to unite the world’s antagonisms.
According to Leibniz, God created the “best possible world”. His world consists of prime elements or atoms which Leibniz called “Monads”. He says:
The Monad, of which we shall speak here, is nothing but a simple substance, which enters into compounds. By ‘simple’ is meant ‘without parts’.
All Monads differ from each other:
Indeed, each Monad must be different from every other. For in nature there are never two beings which are perfectly alike and in which it is not possible to find an internal difference, or at least a difference founded upon an intrinsic quality.
Monads are beings, simple beings. Fundamentally,
[…] nothing but this (namely, perceptions and their changes) can be found in a simple substance. It is also in this alone that all the internal activities of simple substances can consist.
Leibniz regarded it as a “metaphysical necessity”
that every created being, and consequently the created Monad, is subject to change, and further that this change is continuous in each.
These central statements are to be found in the small booklet written in 1714, which was published four years after Leibniz’ death as Monadology.
This way of thinking is radically antagonistic to Descartes. Whereas Descartes presumed two substances (extension and thought), Leibniz presumed (actual) infinitely many (the Monads). In other words, whereas Descartes had principles, Leibniz had individuals.
Leibniz’ wider conceptions of the world are not connected to his mathematical thinking. The principal idea is: Monads are nothing else than perception as well as their change, an important assumption which underlies his entire philosophy. Even if he does not mention this explicitly, he intends it to be a fundamental fact. We will soon recognize this.
Leibniz’ Mathematical Writings
Leibniz never worked as a regular mathematician. Nonetheless he is, together with Isaac Newton, one of the two creators of that mathematical theory which developed into the most powerful of all, till today: calculus.
Leibniz documented his invention in a lengthy essay; the longest mathematical text he ever compiled. It was supposed to be printed in Paris after Leibniz’ departure from the town. But this did not happen and eventually the manuscript was lost. Leibniz, much later, refused to rewrite the paper: in his eyes, too much time had passed already.
However, among the vast amount of papers left by Leibniz, some drafts of this essay were found. An extract from such a draft was first published by Lucie Scholz in her dissertation in 1934, a complete version in 1993 by Eberhard Knobloch and meanwhile (2012) also in Leibniz’ Schriften; a French translation by Marc Parmentier appeared in 2004 and a German translation by has been available since 2007 via the internet and since 2016 as a book.
Reading Leibniz’ papers (which is not very easy as he wrote mostly in Latin) repudiates all the prejudices of present-day scientists against their predecessors: they were less intelligent than we are, their ideas were more vague, their reasonings inconclusive—only today are we qualified to be exact and precise.
The point is this: many earlier scientists did not use “vague” notions and “diffuse” reasonings—but completely different ones. If one engages with those different concepts and follows these other ways of reasoning, one realizes that Leibniz’ proofs are not incorrect at all. Quite the opposite, Leibniz’ ideas are marked by great ingenuity. His proofs, judged by today’s standards, are as precise as his concepts allowed for.
Especially the following three concepts: convergence, integral and differential stand out as great scientific achievements.
Leibniz’ Theorem: Fresh from the Creator!
The Convergence of Infinite Series
Up until today the basic curriculum of higher mathematics contains “Leibniz’ Theorem”. It is about infinite series, such as
or
As series are infinite sums, it is not possible to calculate them directly. Nevertheless, they often have a value, a sum. The two above happen to have a sum, but others do not. The series
or
do not have a sum, that is to say: no finite value.
If one ponders for a while perhaps the following idea may arise: promising candidates for series with a sum may be those which fulfil two conditions: (i) the summands, their terms are always decreasing and can become as small as one likes them to be; (ii) their signs alternate.
Consequently, the first term is greater than the sum, as the second term is taken away from it; the sum of the first two terms is smaller than the sum, as the third term is added to it: condition ii., etc. Finally: the difference (a change!) between the successively calculated sums decreases and becomes arbitrarily small: condition i.
This phenomenon that “the sum becomes increasingly more accurate if the differences between sums, which can truly be calculated, decrease below each given quantity” is what we call “convergence” today. Yet, during Leibniz’ time this name was not established.
Leibniz’ Formulation of His Theorem
In his manuscript Leibniz wrote:
If a quantity A is equal to a series b − c + d − e + f − g, etc.,
$$\displaystyle \begin{aligned} A = b-c+d-e+-\ldots\,,\end{aligned}$$which decreases infinitely in such a way that the terms eventually become smaller than an arbitrarily given quantity, it will be
greater than A, so that the difference is smaller than c
smaller … … is smaller than d
greater … … smaller than e
+ b − c + d − e smaller … … smaller than f.
And in general, the part of the decreasing series with alternating additions and subtractions, which ends with an addition, will be greater than the sum of the series, the part which ends with a subtraction will be smaller; but the error or the difference will always be smaller than the term of the series, which follows the part at once.
With the exception of the line “A = b − c + d − e + −…” and the last three “is smaller than”, this is exactly what Leibniz wrote in his manuscript. It is as precise as possible. Leibniz describes in all detail what an “infinite series” with “alternating signs” and “steadily decreasing” terms which “decrease below each assumed quantity” is.
It is permissible to read this statement of Leibniz as follows:
Theorem. If the terms of a series
$$\displaystyle \begin{aligned} b-c+d-e+-\ldots \end{aligned}$$decrease indefinitely (i.e. they eventually get less than any assumed quantity) than this series has a finite sum.
Leibniz did not leave it at this description but added a fairly detailed proof.
Leibniz’ Proof of His Theorem
Leibniz’ proof consists of a preliminary consideration and four steps.
Preliminary: as the amount of the terms steadily decreases, there is altogether more added than subtracted. Added were b + d + f + …, subtracted were c + e + g + … and we have b > c, d > e, f > g, etc. In this manuscript Leibniz does not use a “greater” sign, but in others he does.
Especially we have for the sum A:
-
1.
The first step of the proof: using the last inequality we may consider the number
$$\displaystyle \begin{aligned} b-A\,.\end{aligned}$$(We see: Leibniz tries to deal with positive, true numbers!) Therefore,
$$\displaystyle \begin{aligned} b-A=b-(b-c+d-e+f-g+-\ldots)=c-d+e-f+g-+\ldots<c\,,\end{aligned}$$where the last inequality < holds for the same reason as was given for A < b in the preliminary!
-
2.
The second step of the proof: we found that A < b. In the same way we derive from (1) that
$$\displaystyle \begin{aligned} A>b-c\,.\end{aligned}$$Is it?—Really!—Therefore, it is allowed to take A − (b − c) (which is also a true number) and we get
$$\displaystyle \begin{aligned} A-(b-c)=d-e+f-g+-\ldots<d\,,\end{aligned}$$by the same argument.
-
3.
Leibniz’ third step of the proof: as before, through rearranging the result above, we get as the next starting point:
$$\displaystyle \begin{aligned} A<b-c+d\,.\end{aligned}$$So we can build (b − c + d) − A. And by the same procedure we arrive at
$$\displaystyle \begin{aligned} b-c+d-A=e-f+g-+\ldots<e\,.\end{aligned}$$
Leibniz adds a fourth step in the same manner, but we need not repeat it here, as the pattern is clear by now.
As a result Leibniz gets a sequence of inequalities:
From the second line onwards we have on the left side the error that arises, if instead of the whole series only its beginning till the nth term is taken and the right hand side shows that this error is always less than the (n + 1)st term. But it was presupposed that the terms’ magnitude “eventually decrease below any assumed magnitude”, and, therefore, this assumption—as can be seen in the above inequalities—leads to the conclusion that the the error caused by breaking off the series also becomes less than any assumed magnitude.
What more do we want?

And that even today. Leibniz did so in his manuscript of late summer 1676.
Reflection on Leibniz’ Achievement
Through these notes Leibniz became the first person in the history of mathematics to describe, as precisely as possible, what is nowadays called the “convergence” of an “(infinite) series”. (The attribute “infinite” is plainly superfluous but it sounds so breathtakingly bombastic.)
The expression “convergence” was not used by Leibniz. However, the importance is the content of the finding, the name is quite irrelevant. What counts is that Leibniz stated his result in absolute clarity.
The philosophical question: what did Leibniz do? What was the object of his inquiry?
My answer: obviously, Leibniz explored a variable quantity, i.e. the successively calculated sum of a series. Today this is called the “partial sum” and we have a standard symbol for it: sn. We write:
It is evident that this object, the “partial sum” or sn, is a variable (i.e. changing) quantity. Leibniz only had the right hand sides of the above equations and, therefore, they can be named without any reservations (“sn” will do as well as any other name).

Leibniz’ way of arguing is so fascinating, so deeply mathematical that nobody dared to characterize it as “unmathematical” and to criticize it: According to the standards of classical mathematics this is not mathematics!—At least to our knowledge nobody dared to make such an accusation, written or otherwise.
An Idea Which Leibniz Could not Grasp and the Reason for His Inability
Today we illustrate the above facts by the following picture:

At a single glance we grasp the situation. However,

For this picture demands two things: (a) lengths have a direction, and (b) “negative” numbers do exist.
Actually we have seen earlier that a length has no direction! Moreover, if negative numbers were true “numbers”, some of the more than two thousand years old laws (known at least since Euclid!) would be invalidated.
One of these laws reads as follows:
But if − 1 is a “number”, this law requires:
and thus a contradiction. Contradictions are absolutely forbidden in mathematics for otherwise everything whether false or correct can be proved.
The mathematicians of the late seventeenth century and the beginning of the eighteenth century had to make a decision: should those time-honoured laws be preserved, or should − 1 become a true number?
Leibniz was an astoundingly creative thinker but not a revolutionary; he was a diplomat. He shunned revolutions (the dismissal of the validity of these classical laws) but praised the news by couching it in unctuous words:
Nevertheless, I do not want to deny […] that − 1 is a quantity smaller than nothing; this only has to be understood right-minded. Such statements are what I call passable true (following the renowned ); […] However, they would not bear a severe verification, but yet they are of great help for the calculation and of immense value for the inventive genius as well as for universal concepts.
The classical phraseology of diplomats: “… / as well as …”; “− 1 is smaller than 1 / but this has to be correctly understood”; “to be on the safe side, I cite an authority, however, unknown or vague, or hint at my obedience: strictly speaking this is forbidden / but it is of huge utility”.
Thus, the paper published by Leibniz in a famous scientific journal in April 1712 can be understood as an act of great political diplomacy.
The quintessence is:
If he or she may say something like: “this law is valid only for positive numbers, and all is fine”, the known contradictions are outlawed. (Hopefully, no others will appear we have not yet thought of!)
The Precise Calculation of Areas Bounded by Curves: The Integral
The Beginning Is Easy
Lasting for thousands of years, the Babylonians operated quite differently compared with classical Greek scholars, but in Greek culture the following art of planimetry was taught:
It only allowed for rectangles. The area is

From this all further calculations had to be deduced, e.g.: the area of a rectangular triangle is

The Problem
What happens, if the boundary of one side is curved?

The Solution of Leibniz—The Original Way
For such an instance Leibniz has the following astounding idea:
I present Leibniz’ original figure, omitting what is not essential to the principal idea. Even so, the figure is still sufficiently complicate (Fig. 3.1).
The object of the construction is the area between the curve D1, D2, D3, D4 and the three line segments \(\overline {D_1 B_1}\), \(\overline {B_1 B_4}\) , and \(\overline {B_4 D_4}\) . The points Dn are any points on the curve.
-
1.
Leibniz takes the stairway B1, N1, P1, N2, P2, N3, P3, B4, B1 as a first approximation of the area. In the following and for the sake of simplicity we will indicate the single steps of the stairway by their dotted “upper” lines, the “step zones”, i.e. N1 P1, etc.
-
2.
Now let us assess the error of this approximation! It consists of the sum of partial errors. Compared with the actual area we get:
-
(a)
The first step N1 P1 is too big by the (curved) triangle D1 N1 F1—as well as too small by the triangle F1 P1 D2. Leibniz is saying that at any rate this first partial error is less than the whole rectangle in between D1 and D2. This is really generous, isn’t it!
-
(b)
The same with the following step N2 P2, again the second partial error caused by the approximation is clearly less than the rectangle in between D2 and D3.
-
(c)
And so forth.
-
(a)
-
3.
So what is the total error at most? Most likely it is less than the sum of the partial errors; undoubtedly it is less than the sum of the rectangles D1, D2; D2, D3 and D3, D4.
-
4.
Therefore, what is our estimate of the total error? The total height is obviously (if the curve is always ascending or always descending; otherwise it must be divided in such way) the height from D1 to D4. And, to be on the safe side, Leibniz chooses as width the maximal width of the steps \(\overline {B_1 B_2}\), \(\overline {B_2 B_3}\) and \(\overline {B_3 B_4}\). In the example it is \(\overline {B_3 B_4}\).
Outcome: the total error of the first approximation is clearly less than the product of the height from D1 to D4 and the maximal width of the \(\overline {B_n B_{n+1}}\).
-
5.
All boils down to the following conclusion:
The points D on the curve are completely arbitrary. We may choose as many of them as we please. Let’s say, we choose k equidistant points such that the steps have width
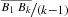 .
.Consequently, the total error of this kth approximation will be certainly less than the rectangle with width
 and height \(\overline {D_1\,D_k}\) (more precisely, \(\overline {B_1\,D_k}\)).
and height \(\overline {D_1\,D_k}\) (more precisely, \(\overline {B_1\,D_k}\)).Whereas the height of the rectangle remains the same, its width continuously decreases if further points D are chosen. And the total error of the kth estimate is clearly less than the area of the corresponding rectangle.
Subsequently, the product of these two values will also drop: if in the product bk ⋅ h the factor bk is constantly decreasing while h (the height) remains the same, the product decreases, too.
Thus the total error of the estimate reduces further.
-
6.
How small does it become?
Obviously, there is no lower limit to the area’s magnitude (actually, its “smallness”): with the exception of the limit zero, of course. According to Leibniz’ own words:
The points D may be thought of as near and in such a great number that the straight-lined step-shaped area differs from the four-lined area D1 B1 B4 D4 D3 etc. D1 itself by a quantity which is less than an arbitrarily given.
This means: the total error which emerges from the calculation of the area below the steps instead of the area limited by the curve, can be decreased to any desired degree of exactitude.
Did we hit the jackpot? Do we have the area?—Yes and no. On the one hand, we have a method of calculation: Leibniz is capable of calculating the area as precisely as he wants to.
On the other hand, being able to calculate something does not mean to have a concept for doing it. Engineers may be satisfied with a method of calculation, but mathematics needs concepts! In this case, an appropriate concept of numbers. However, Leibniz could not offer one. Understandably so, as it turned out mathematics needed two further centuries to coin such concepts (Chaps. 13 and 12) and in a certain sense, these solutions contradict Leibniz’ thinking, for they demand the acceptance of the “actual infinite” in mathematics (see Chap. 5).
Outlook
Leibniz’ idea from 1676 provided the foundations for what was later called “integration”, especially for the “integral” of a “function”, the graph of which Leibniz still called “curved line”.
However, the names “integral” as well as “function” were already used by Leibniz, but both with other meanings.
-
(a)
“Function” was Leibniz’ title for a multitude of line segments which can be constructed to make up a curve when set in relation to straight coordinate axes: abscissa, ordinate, tangent, normal, sub-tangent, sub-normal, resecta, …, a lot of special geometrical constructions, which were frequently studied in his times.

-
(b)
The name “integral” was invented by Johann Bernoulli and in 1690 his brother used the notation for the first time in a printed paper. The first printed document in which Leibniz used the sign “
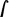 ” dates back to the year 1686. He used it in connection with his sign for the “differential”: “ dx ”—a concept which will be treated in the next section. As “d” is an operator, “ dx ” as well as “ dy ” are to be read as a single quantity in the following text.
” dates back to the year 1686. He used it in connection with his sign for the “differential”: “ dx ”—a concept which will be treated in the next section. As “d” is an operator, “ dx ” as well as “ dy ” are to be read as a single quantity in the following text.If one transforms the differential equation p dy = x dx into the “summatorial” [by building the sums on both sides], one has
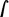 p dy =
p dy = 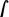 x dx . From what I have shown in the method of tangents, we clearly have \(d(\frac {{1}}{{2}}\,xx)=x\,dx\); therefore, the reverse is \(\frac {{1}}{{2}} xx=\)
x dx . From what I have shown in the method of tangents, we clearly have \(d(\frac {{1}}{{2}}\,xx)=x\,dx\); therefore, the reverse is \(\frac {{1}}{{2}} xx=\) 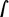 x dx (because like powers and roots in usual calculations, we have sums and differences or
x dx (because like powers and roots in usual calculations, we have sums and differences or 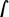 and d as reciprocal).
and d as reciprocal).
The first evidence of the integral sign, as it is still used today, “\(\int \)”, goes back to 1691. Leibniz had encountered the name “integral” for the first time in 1690, in an article by
However, the topic that was presented above, i.e. the exact calculation of an area with a curved boundary, was made the subject of mathematics, as precisely as 1676, only 178 years later. According to its later inventor Bernhard Riemann, the mathematical object is nowadays known as the “Riemann integral”. Shortly before Riemann, Cauchy had come up with a similar idea (pp. 145f).
To sum up: Leibniz had already developed this notion as precisely as possible—but without today’s concepts of “function”, “infinite series”, and “convergence”. It worked without these notions!
If Leibniz’ plan had succeeded and his manuscript had been printed, mathematics would have developed differently.
Leibniz’ Neat Construction of the Concept of a Differential
The First Publication: A False Start
Leibniz published his idea of “differential” from the 1670s in October 1684. Albeit, his explanation remained very vague. Even worse, Leibniz made a mistake such that the intelligent reader had to decide whether the whole treatise was wrong or merely the definition of its fundamental notion. In case of the latter, the reader had to reconsider the correct concept of “differential” all by himself.
Clearly, this publication was almost a complete failure. Where to find a clever and astute reader? had tried hard to understand this text since 1687. In the end he needed two or three years to understand the main idea in order to use the new method himself. What’s more, he was able to develop it further, in dialogue with his younger brother Johann—and with Leibniz.
Another False Start: The New Edition
The differential calculus consists of the concept of “differential” as well as laws of calculation for those differentials. Without these laws the concept is of no use.
Leibniz owed the explicit formulation and the detailed foundation of these laws to the public of his time. Just as before, he wrote a manuscript thereon but did not publish it. In 1846, when it was finally published, together with a lot of other manuscripts on this topic, nobody took notice. The same happened in 1920, when the English translation appeared. This fact has been documented only fairly recently: by in 1972 and by in 2013, who are both historians of mathematics.
The Neat Construction, Part I
In regard to the above presentation it comes as no surprise that Leibniz took also the “differential” to be a geometrical notion. More precisely, with help of the “differential” it should become possible to draw a tangent to an arbitrary curved line (Fig. 3.2).
A “tangent” is a straight line that touches the curve, i.e. that snuggles up to it. To touch usually means there is no cut, the curve remains on the one side of the straight line. However, there are unusual curves and sometimes the “tangent” still cuts those curves.
Leibniz came up with the following geometrical construction of the differential. The abscissa x is drawn upwards, the ordinate y to the right (today we usually do it the other way round). Take a parabola
which is represented by the curved line in the figure. Leibniz chooses AX1 = x and X1Y1 = y. From the point Y1 the perpendicular line Y1D to the larger horizontal line X2Y2 (the ordinate) is drawn. The difference of AX2 and AX1 is called by Leibniz the “differential” dx , similarly, the difference of X2Y2 and X1Y1 is called the “differential” dy . These are the notations, now the calculations:
The equation of the curve reads
Leibniz starts by changing x to x + dx and subsequently y to y + dy . This modifies the equation to:
We subtract the original equation and get:
Of course, dx and dy are changing quantities. And as we would expect they decrease indefinitely: below any given quantity.
Therefore, the numerator of the fraction will approach 2x. But then, as zero is not allowed as denominator, we encounter a problem regarding the dx on the left side of the equation. Yet, if dx does not truly reach its limit zero, the numerator on the right will not become = 2x.
What are we to do?
Interlude: The General Rule: The Law of Continuity
Leibniz needs an argument that enables him to extend the validity for cases only holding for dx ≠ 0 to the case dx = 0.
And indeed, Leibniz really had such an argument at his disposal: his Law of Continuity. According to the historian of mathematics , this cognitive law has a similar significance and power for Leibniz as later the Method of Dialectics has for . It is a “universal scheme of thought and cognition”. And as we might expect, coming from Leibniz, its main characteristic is a diplomatic rather than a logical one. The Law of Continuity unites opposites instead of separating them as logic does.
This is the principal idea. Naturally, the law may be given some more precise formulation, in accordance with the concrete requirement.
Thus, in order to give his concept of “differential” a rigorous foundation, Leibniz formulated his Law of Continuity in his manuscript as follows:
If some continuous transition ends in some limit, it should be allowed to state a common law of thought that includes the last limit.
This bails him out.
The Neat Construction, Part II
Leibniz takes the differential triangle Y1 D Y2. It is his idea to oppose it to an auxiliary triangle with two features: (a) It is similar to the differential triangle. (b) One of its sides is fixed.
This auxiliary triangle originates by producing the side Y2 Y1 to T on the axis A X2.
The auxiliary triangle T X1 Y1 has the same angles as the differential triangle and is, thus, similar to it.
Then point Y2 moves on the curved line (in our example: the parabola) toward the point Y1. What is going to happen?
Point T moves along the vertical axis A X2 up and down, whereas the side X1 Y1 remains fixed. However, the differential triangle Y1 D Y2 and the auxiliary triangle T X1 Y1 remain similar (if the latter triangle degenerates, one has to think anew).
Next, if point Y2 coincides with point Y1, we have exactly the situation which is covered by the Law of Continuity in its above specification: the coinciding of the points Y2 and Y1 represents the limit; the case in which the differential triangle has vanished. However, the auxiliary triangle survives the coinciding of Y2 and Y1—for its side X1 Y1 is fixed and cannot vanish. Therefore, this auxiliary triangle T X1 Y1 represents the common principle which covers both cases the vanishing differential triangle and its disappearance.
Both triangles are similar. Consequently, we have
Leibniz already knows: \(\frac {{\mathit {\,dy}\,}}{{\mathit {\,dx}\,}} = \frac {2x+{\mathit {\,dx}\,}}{a}\). So all together he has:
Actually, Leibniz can apply his Law of Continuity: on the left there is a fraction in which numerator and denominator vanish together; the middle is a fraction with changing value but both, numerator and denominator, remain and stay finite; on the right there is a fraction with vanishing dx in the numerator but all other quantities remain fixed.
Next, Leibniz lets the dx vanish, i.e. dx → 0. The outcome is obvious:
which is with the help of his Law of Continuity absolutely neatly derived—although on the left is a fraction where numerator as well as denominator tend toward zero!
This is exactly the point! Leibniz does not divide 0 by 0 but analyzes a ratio \(\frac {{\mathit {\,dx}\,}}{{\mathit {\,dy}\,}}\) with simultaneously (or, at the same time—but we should keep time out of mathematics!) vanishing terms. In today’s notation: \(\lim \limits _{{\mathit {\,dx}\,}\!\to 0}\frac {{\mathit {\,dy}\,}}{{\mathit {\,dx}\,}}=\frac {2x}{a}\). The auxiliary triangle provides Leibniz with a fixed point to unhinge the world. The Law of Continuity, invented by him, allows him the precise calculation of this ratio  even in the case where dx → 0 as well as dy → 0.
even in the case where dx → 0 as well as dy → 0.
What Is x (and What Is dx) for Leibniz?
Leibniz develops the differential as a geometrical concept. He denotes the respective length on the x-axes by “x”. Of course, this length is not invariable—just the opposite! For Leibniz the length x is changing and this change is described by “x + dx ”.

We know, Descartes denoted by “x” a certain fixed number or length. Leibniz revolutionized Descartes’ world of concepts completely! Only the letter “x” survived—as if nothing had happened. But an upheaval took place: the continuum was introduced in the calculations on the quiet.
Of equal importance is that Leibniz created dx as a changing quantity which decreases below any given quantity. This circumstance was named by him an “infinitely small quantity”.
Consequently, an “infinitely small quantity” is for Leibniz nothing supernatural, inconceivable—but only a special case of a commonly used changing quantity: just one which decreases indefinitely (although Leibniz had no “negative” numbers).
Using the concept “limit” one may say: for Leibniz an “infinitely small quantity” is a changing quantity with zero as its “limit”.
Literature
Arthur, R. T. W. (2013). Leibniz’s syncategorematic infinitesimals. Archive for History of Exact Sciences, 67, 553–593.
Bernoulli, J. (1690). Op. XXXIX. Analysis problematis antehac propositi. In Opera, S. T. (Vol. 1), pp. 421–426. Genevæ: Hæredum Cramer & Fratrum Philbert, 1744. Acta Erud., Mai 1690, pp. 217–219; cf. Bos 1974, p 21.
Bos, H. J. M. (1974). Differentials, higher-order differentials and the derivative in the Leibnizian Calculus. Archive for History of Exact Sciences, 14, 1–90.
Breger, H. (2016). Kontinuum, Analysis, Informales – Beiträge zur Mathematik und Philosophie von Leibniz. In W. Li (Ed.). Berlin: Springer Spektrum.
Buchenau, A. (1966). Gottfried Wilhelm Leibniz – Hauptschriften zur Philosophie (Vol. 2). In E. Cassirer. Vols. 107, 108 of the series Philosophische Bibliothek. Hamburg: Felix Meiner, 1904–1906.
Gerhardt, C. I. (Ed.) (1846). Historia et Origo Calculi Differentialis a G. G. Leibnitio conscripta. Hannover: Hahn’sche Hofbuchhandlung. https://archive.org.
Hofmann, J. E. (1966). Leibniz als Mathematiker. In W. Totok & C. Haase (Ed.), Leibniz, sein Leben – sein Wirken – seine Welt. Hannover: Verlag für Literatur und Zeitgeschehen.
Knobloch, E. (Ed.) (2016). Gottfried Wilhelm Leibniz: De quadratura arithmetica circuli ellipseos et hyperbolae. Klassische Texte der Wissenschaft. Berlin: Springer. German by Otto Hamborg.
Latta, R. (1898). Leibniz. The Monadology and Other Philosophical Writings. Oxford: Clarendon Press.
Leibniz, G. W. (1982). Monadologie. In Gottfried Wilhelm Leibniz: Vernunftprinzipien der Natur und der Gnade. Monadologie. Vol. 253 of the series Philosophische Bibliothek (pp. 26–69). Hamburg: Felix Meiner. German by Herbert Herring 1956. Also in: Buchenau 1904–06, Vol. II, pp. 435–456, 1714
Leibniz, G. W. (1993). De quadratura arithmetica circuli ellipseos et hyperbolae cujus corollarium est trigonometria sine tabulis. In E. Knobloch (Ed.), Abhandlungen der Akademie der Wissenschaften in Göttingen. Göttingen: Vandenhoeck & Ruprecht.
Leibniz, G. W. (2004) Gottfried Wilhelm Leibniz: Quadrature arithmétique du cercle, de l’ellipse et de l’hyperbole et la trigonométrie sans tables trigonométriques qui en est le corollaire. Lat. text: Eberhard Knobloch (Libraire Philosophique. Paris: J. Vrin), ed.: Marc Parmentier.
Leibniz, G. W. (2011). Die mathematischen Zeitschriftenartikel. In H.-J. Heß & M.-L. Babin (Eds.). Hildesheim, Zürich, New York: Georg Olms Verlag.
Leibniz, G. W. (2012). De quadratura arithmetica circuli ellipseos et hyperbolae. In Leibniz-Archiv Hannover (ed.), Gottfried Wilhelm Leibniz – Sämtliche Schriften und Briefe. Vol. 6 – 1673–1676, Arithmetische Kreisquadratur, of the series VII Mathematische Schriften, pp. 520–676. N 51 (1676). https://www.gwlb.de/leibniz/digitale-ressourcen/repositorium-desleibniz-archivs/laa-bd-vii-6.
Scholtz, L. (1934). Die exakte Grundlegung der Infinitesimalrechnung bei Leibniz. Dissertation thesis, Hohe Philosophische Fakultät der Philipps-Universität Marburg. Görlitz-Biesnitz: Verlagsanstalt Hans Kretschmer.
Author information
Authors and Affiliations
Rights and permissions
Copyright information
© 2022 The Author(s), under exclusive license to Springer Nature Switzerland AG
About this chapter
Cite this chapter
Spalt, D.D. (2022). Lines and Variables. In: A Brief History of Analysis. Birkhäuser, Cham. https://doi.org/10.1007/978-3-031-00650-0_3
Download citation
DOI: https://doi.org/10.1007/978-3-031-00650-0_3
Published:
Publisher Name: Birkhäuser, Cham
Print ISBN: 978-3-031-00649-4
Online ISBN: 978-3-031-00650-0
eBook Packages: Mathematics and StatisticsMathematics and Statistics (R0)



 greater than A, so that the difference is smaller than c
greater than A, so that the difference is smaller than c smaller … … is smaller than d
smaller … … is smaller than d greater … … smaller than e
greater … … smaller than e

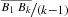 .
. and height
and height 
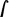 ” dates back to the year 1686. He used it in connection with his sign for the “differential”: “ dx ”—a concept which will be treated in the next section. As “d” is an operator, “ dx ” as well as “ dy ” are to be read as a single quantity in the following text.
” dates back to the year 1686. He used it in connection with his sign for the “differential”: “ dx ”—a concept which will be treated in the next section. As “d” is an operator, “ dx ” as well as “ dy ” are to be read as a single quantity in the following text.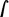 p dy =
p dy = 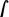 x dx . From what I have shown in the method of tangents, we clearly have
x dx . From what I have shown in the method of tangents, we clearly have 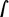 x dx (because like powers and roots in usual calculations, we have sums and differences or
x dx (because like powers and roots in usual calculations, we have sums and differences or 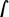 and d as reciprocal).
and d as reciprocal).
