Application and Control of Quadrotors

Abstract

A quadrotor is a multirotor helicopter, boosted by four rotors. In contrast to fixed-wing aircraft, quadrotors are categorized as rotorcraft, since their lift is produced by a set of rotors. The usage of quadrotors has increased in recent years in civilian and military operations. They are adaptable during vertical takeoff and landing and have stability when hovering. Additionally, quadrotors have low power consumption and are unobtrusive.

The many important applications of quadrotors include delivery and monitoring. A quadrotor can fly in an autonomous and non-autonomous manner with use of methods using the proportional integral derivative (PID) and linear quadratic regulator (LQR), sliding mode control, and fuzzy control. Such methods stabilize the quadrotor through flights. The aim of most controllers is to eliminate the error which is the difference between a measured value (measured states by sensors) and a desired set-point (desired states). The “error” can be minimized by adjusting the control inputs and the speed of the motors, in an iterative manner. This chapter illustrates key applications, and further the modeling and control of quadrotors is described in brief. Two cases of studies are presented, the first of which deals with the design of PID control for precise positioning of delivery quadrotors, and the second entails the design of multiple model adaptive control (MMAC) of the quadrotor.

1 Introduction

The study of micro unmanned air vehicles (UAVs) through developing technologies enables expansive application. UAVs are useful in a wide array of operations and have gained importance. UAVs are aircraft which may be flown without a pilot (Newcome 2004).

Modern rotorcraft UAVs have many benefits compared to old-styled crafts, including improved maneuverability, an ability to fly above objectives, and capacity to take off and land in limited space in comparison to fixed-wing crafts. Quadrotors belong to the class of rotorcrafts and are recognized by their simple structure, ease of maintenance, and unsophisticated dynamics in comparison to those of helicopters (Schmidt 2011).

Quadcopters operate in two flight modes: autonomous and non-autonomous. Non-autonomous flights are controlled by the user through a radio device (control joystick) as shown in Fig. 10.1.

Fig. 10.1

Joystick control of a quadcopter through non-autonomous flight (Jung et al. 2018)

In autonomous flight , the quadcopter flies and controls itself, carrying out required missions without user interference. Quadcopters operate with a global positioning system (GPS) sensor to ascertain their linear position in relation to other sensors and achieve a stable and balanced flight. The GPS sensor connects with GPS satellite systems as shown in Fig. 10.2 and uses information provided for operation (Grisso et al. 2009; Rahemi et al. 2014; Ziaul 2016).

Fig. 10.2

Quadcopters control themselves in autonomous flight using a Global Positioning System (GPS)

In the literature, the many types of control methods applied in autonomous or non-autonomous modes include PID (Ferry 2017), LQR (Purnawan et al. 2017), sliding mode (Tripathi et al. 2016; Thomas 2010), fuzzy control (Sattar and Ismail 2017), image recognition (Luo et al. 2016), and adaptive control (Minh et al. 2014), stabilizing and improving their flight performance.

The remaining parts of this chapter are structured as follows: Sect. 10.2 details applications of quadrotor UAVs; Sect. 10.3 presents the modeling of a (six degrees of freedom) quadrotor; Sect. 10.4 discusses quadrotor control; and Sect. 10.5 features two case studies of quadrotor control, the first case demonstrates the design of a PID controller for delivery quadrotor systems and the second shows the design of a Multiple Model Adaptive Control (MMAC) based on three Kalman fiters (KFs). Conclusions and prospective future directions are covered in Sect. 10.6.

2 Applications of Quadrotors

Common quadrotor applications (Air Drone Craze, Drone Deals 2019) are detailed in this section.

2.1 Journalism, Filming, and Aerial Photography

Quadcopters are increasingly popular in photography of sport events, competitions, and cinematography owed to their maneuverability, takeoff, and vertical landing, as well as hovering. Drones have recently started to be used in the direct broadcasting of satellite channels by linking live broadcast cameras to Earth stations, which in turn are transmitted through the satellite channel.

2.2 Shipping/Delivery

One of the most important properties of quadrotors is their ability to be operated autonomously through a range of techniques. Avoiding traffic and jammed roads, UAVs are used to deliver small parcels, letters, medicines, and even pizzas over short distances.

2.3 Disaster Management, Search, and Rescue/Healthcare

The task of rescuing people exposed to hazards or perilous circumstances at night and in difficult terrain is a race against time. Equipped with thermal cameras, quadcopters can be used to locate people and rapidly assess situations.

2.4 Geographic Mapping

The ability of the quadcopter to reach/overview uneven terrain enables its use in the collection of accurate information with high-precision cameras for geographic mapping .

2.5 Structural Safety Inspections

The quadcopter is used by various sectors to provide accurate assessment, such as in checking building structures, electric power lines, and crude oil pipelines. Increased visual clarity and thermal, water, and gaseous sensors allow identification of potential future problems, in order that one may take appropriate measures to prevent them from happening.

2.6 Precision Agriculture

Quadcopters help farmers to closely monitor agricultural fields, enabling them to improve management and increase production. Quadcopters are additionally used in spraying pesticides, covering vast areas in a fast and consistent manner, with improved coverage while losses of pesticides are reduced.

2.7 Wildlife Monitoring/Poaching

The quadcopter assists security services charged with protection of remote, wild areas by detecting hunters trapping rare animals, often useful where extinction is a very present threat. They may also be used to detect the positions of sick animals more quickly allowing necessary actions to be carried out to help and preserve them.

2.8 Law-Enforcement and Border Patrol

The quadcopter assists the police and security services in law enforcement operations, especially in preventing the smuggling of drugs and prohibited substances by monitoring external and internal borders of countries.

2.9 Construction Sites

Quadcopters help to provide three-dimensional vision of construction stages, thus enabling engineers to detect errors early for process and increased safety of projects.

2.10 Entertainment

Plenty of hobbyists are picking up quadrotors to play around with, both in remote flight and by programming quadrotor AI (artificial-intelligence). As such quadrotors can be used in many ways to capture videos and photographs.

2.11 Military and Law Enforcement

The quadcopter is used extensively in military fields today to carry out multiple tasks including reconnaissance and surveillance of enemy sites (Armed Quadrotors Are Coming 2014). For example, a small UAV may be used in provision of visual surveillance of a drug trafficker’s compound deep in the jungle (Dhanalakshmi et al. 2015).

3 Modeling of Quadrotors

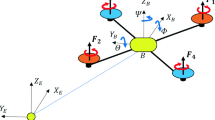
Generally, a quadcopter is characterized by four independently controllable actuators (motors) assembled in a cross configuration as shown in Fig. 10.3. The actuators are two clockwise (CW) and two counterclockwise (CCW), so the affected rotational torque on the body around the Z axis of the quadcopter is cancelled during the hovering state (Allen 2014; Quadcopter 2017; Fernando et al. 2013). The figure shows two basic coordinate frames called inertial frames , being a fixed earth frame and body frame. The two frames are used to identify the quadrotor’s locations and attitude in order that translation and rotation matrices can be applied to transfer the vehicle from one coordinate frame to another (Fernando et al. 2013; Alaiwi and Mutlu 2018).

Fig. 10.3

The inertial and body frames of a quadrotor

In this section, the performance of unmanned rotorcraft is demonstrated using a six degree of freedom (6-DoF) prototype model . The quadrotor includes four propellers responsible for lift force. Propellers are driven by four motors that are fixed onto a frame with a plus shape structure. Dynamic modeling is usually developed using the Newton Euler Formula , where the drive force and produced torque are regarded as the main quadrotor control elements (Magnussen and Skjonhaug 2011).

Quadrotor control is taken into consideration as a multivariable and as a substitute nonlinear system due to its dynamics, having sturdy coupling among translation and angular motion, and suffers from external disturbances related to flight surroundings and the effect of huge payload variability. These factors demand a robust control design. The control goal is to allow for sudden changes and rewards an ability of discovering improved tracking performance in contrast to any modeling error and uncertainty.

The quadrotor has a linear position ξ = (x, y, z) and the attitude (angular position) defined by Euler angles H = (roll (ϕ), pitch (𝜃), yaw (ψ)) with respect to the inertial frame. The Euler angles determine the rotation of the quadrotor around each axis (x, y, and z axis, respectively). The roll angle determines rotation around the x-axis, while the pitch angle determines rotation around the y axis and the yaw angle determines rotation around the z-axis. The angular velocity in the body frame V = [p, q, r] can be related to the Euler angles velocities ($\dot{x}$, $\dot{y}$, $\dot{z}$) in the same frame by the following relation:

$$ V={W}_H\dot{\theta} $$

$$ \left[\begin{array}{c}p\\ {}q\\ {}r\end{array}\right]=\left[\begin{array}{ccc}1& 0& -{s}_{\theta}\\ {}0& {c}_{\phi }& {c}_{\theta }{s}_{\phi}\\ {}0& -{s}_{\phi }& {c}_{\theta }{s}_{\phi}\end{array}\right]\left[\begin{array}{c}\dot{\phi}\\ {}\dot{\theta}\\ {}\dot{\psi}\end{array}\right] $$

(10.1)

where c_ϕ =  cos (ϕ), s_ϕ =  sin (ϕ), c_θ =  cos (θ), s_θ =  sin (θ), and W_H is the transformation matrix for angular velocities from the inertial frame to the body frame. Conversely, a rotation matrix (R) can be used to transform the linear velocity (η = [u v w]) from the body frame to the inertial frame. The matrix R has an orthogonal property, so R^T = R⁻¹ (Castillo–Zamora et al. 2018; Bouzgou et al. 2017; Gordon et al. 2016).

$$ R=\left[\begin{array}{ccc}{c}_{\psi }{c}_{\theta }& {c}_{\psi }{s}_{\theta }{s}_{\phi }-{s}_{\psi }{c}_{\phi }& {c}_{\psi }{s}_{\theta }{c}_{\phi }+{s}_{\psi }{s}_{\phi}\\ {}{s}_{\psi }{c}_{\theta }& {s}_{\psi }{s}_{\theta }{s}_{\phi }+{c}_{\psi }{c}_{\phi }& {s}_{\psi }{s}_{\theta }{c}_{\upphi}-{c}_{\psi }{s}_{\phi}\\ {}-{s}_{\theta }& {c}_{\theta }{s}_{\phi }& {c}_{\theta }{c}_{\phi}\end{array}\right] $$

(10.2)

The quadrotor has four motors which are used to provide it with the required thrust force (T), moving in the direction of the body z-axis. These are calculated via (10.3) and (10.4) as

$$ T={\sum}_{i=1}^4{T}_i=k\left({w}_1^2+{w}_2^2+{w}_3^2+{w}_4^2\right) $$

(10.3)

$$ {T}_i={f}_i=k{w}_i^2 $$

(10.4)

where T_i is the thrust force generated by the ith motor, k is the thrust factor, and w_i is the angular velocity of the ith motor. The motors provide the quadcopter with required torques τ_ϕ, τ_θ, and τ_ψ in the direction corresponding to the body frame (Alaiwi and Mutlu 2018; Bouzgou et al. 2017). This is further expanded in (10.5) as follows:

$$ {\tau}_B=\left[\begin{array}{c}{\tau}_{\phi}\\ {}{\tau}_{\theta}\\ {}{\tau}_{\psi}\end{array}\right]=\left[\begin{array}{c} lk\left(-{w}_2^2+{w}_4^2\right)\\ {} lk\left(-{w}_1^2+{w}_3^2\right)\\ {}k\left({w}_2^2+{w}_4^2-{w}_1^2-{w}_3^2\right)\end{array}\right]=\left[\begin{array}{c}l{U}_2\\ {}l{U}_3\\ {}{U}_4\end{array}\right] $$

(10.5)

where l is the distance from the centre of the motor to the center of mass of the quadrotor; U₂, U₃, and U₄ are input forces to the quadrotor generated by motors. These forces can be calculated as

$$ {U}_2={f}_2-{f}_4=k\left(-{w}_2^2+{w}_4^2\right) $$

(10.6)

$$ {U}_3={f}_1-{f}_3=k\left(-{w}_1^2+{w}_3^2\right) $$

(10.7)

$$ {U}_4={f}_2+{f}_4-{f}_1-{f}_3=k\left({w}_2^2+{w}_4^2-{w}_1^2-{w}_3^2\right) $$

(10.8)

Each motor generates an extra torque ${\tau}_{{\mathrm{m}}_i}$ around its rotor axis which can be calculated by

$$ {\tau}_{{\mathrm{m}}_i}={dw}_i^2+{I}_{\mathrm{m}}{\dot{w}}_i $$

(10.9)

where d, ${\dot{w}}_i$, and I_m represent the drag factor, the angular acceleration of the ith motor, and the inertia moment retrospectively. Generally, ${\dot{w}}_i$ is very small and can be omitted, leading to (10.10)

$$ {\tau}_{m_i}={dw}_i^2 $$

(10.10)

The quadrotor is assumed to be symmetric, so its inertia matrix I is diagonal with I_xx = I_yy. The inertia matrix of quadcopter around three axes can be represented as

$$ I=\left[\begin{array}{ccc}{I}_{xx}& 0& 0\\ {}0& {I}_{yy}& 0\\ {}0& 0& {I}_{zz}\end{array}\right] $$

(10.11)

The linear acceleration $\left(\ddot{x},\ddot{y},\ddot{z}\right)$ and angular acceleration $\left(\ddot{\phi},\ddot{\theta},\ddot{\psi}\right)$ equations are used to represent the dynamic motion equations of the quadrotor. These functions can be derived by Euler-Lagrange equations of motion and Eqs. (10.1, 10.2, 10.3, 10.4, 10.5, 10.6, 10.7, 10.8, 10.9, 10.10, and 10.11) shown above.

The Lagrange equation variable is key in derivation of linear and angular acceleration equations. The Lagrange equation represents the algebraic sum of translational (E_trans), rotational (E_rot), and potential (E_pot) energies. It can be defined as (Alaiwi and Mutlu 2018)

(10.12)

where $o=\left[\begin{array}{c}\xi \\ {}H\end{array}\right]={\left[x,y,z,\phi, \theta, \psi\ \right]}^T$.

Quadcopters are exposed to external forces such as wind that affect the copter’s torques. The relationship between external forces and torques can be represented by the following:

(10.13)

Linear and angular components are not independent so should be studied separately. Therefore, the linear Euler-Lagrange equations are

$$ f=R{T}^B=m\ \ddot{\xi}+ mg\left[\begin{array}{c}0\\ {}0\\ {}1\end{array}\right] $$

(10.14)

where T^B is the thrust force vector in the direction of body axis and T^B = [0 0 T]^T. Therefore,

$$ \ddot{\xi}=\frac{R}{m}\left[\begin{array}{c}0\\ {}0\\ {}T\end{array}\right]-g\left[\begin{array}{c}0\\ {}0\\ {}1\end{array}\right] $$

(10.15)

Equation (10.2) is substituted in Eq. (10.15) to get the following:

$$ \left[\begin{array}{c}\ddot{x}\\ {}\ddot{y}\\ {}\ddot{z}\end{array}\right]=\frac{T}{m}\left[\begin{array}{c}{c}_{\psi }{s}_{\theta }{c}_{\phi }+{s}_{\psi }{s}_{\phi}\\ {}{s}_{\psi }{s}_{\theta }{c}_{\phi }-{c}_{\psi }{s}_{\phi}\\ {}{c}_{\theta }{c}_{\phi}\end{array}\right]-g\left[\begin{array}{c}0\\ {}0\\ {}1\end{array}\right] $$

(10.16)

As we mentioned earlier, the symbol T represents the thrust force generated by motors. We will replace it with U₁ to format all symbols that represent the forces generated by quadcopter’s motors.

$$ \left.\begin{array}{c}\ddot{x}=\frac{U1}{m}\left({c}_{\psi }{s}_{\theta }{c}_{\phi }+{s}_{\psi }{s}_{\phi}\right)\\ {}\ddot{y}=\frac{U1}{m}\left({s}_{\psi }{s}_{\theta }{c}_{\phi }-{c}_{\psi }{s}_{\phi}\right.\\ {}\ddot{z}=\frac{U1}{m}{c}_{\theta }{c}_{\phi }-g\end{array}\right\} $$

(10.17)

where m represents the mass of the quadrotor.

The relations between angular velocity of motors w_i and generated forces U₁, U₂, U₃, and U₄ by motors can be presented in a matrix form (Armah et al. 2016; Herrera and Gómez 2015).

$$ \left[\begin{array}{l}{w}_1^2\\ {}{w}_2^2\\ {}{w}_3^2\\ {}{w}_4^2\end{array}\right]=\left[\begin{array}{cccc}\frac{1}{4k}& 0& \frac{-1}{2k}& \frac{-1}{4d}\\ {}\frac{1}{4k}& \frac{-1}{2k}& 0& \frac{1}{4d}\\ {}\frac{1}{4k}& 0& \frac{1}{2k}& \frac{-1}{4d}\\ {}\frac{1}{4k}& \frac{1}{2k}& 0& \frac{1}{4d}\end{array}\right]\left[\begin{array}{c}{U}_1\\ {}{U}_2\\ {}{U}_3\\ {}{U}_4\end{array}\right] $$

(10.18)

The angular Euler-Lagrange equations can be defined as follows:

$$ {\tau}_B=J\ddot{H}+C\left(H,\dot{H}\right)\dot{H} $$

(10.19)

where J is the Jacobian matrix transform from V to $\dot{H}$ and can defined as follows:

$$ J={W}_H^TI{W}_H=\left[\begin{array}{ccc}{I}_{xx}& 0& -{I}_{xx}{s}_{\theta}\\ {}0& {I}_{yy}{c}_{\upphi}^2+{I}_{zz}{s}_{\phi}^2& \left({I}_{yy}-{I}_{zz}\right){c}_{\phi }{s}_{\phi }{c}_{\theta}\\ {}-{I}_{xx}{s}_{\theta }& \left({I}_{yy}-{I}_{zz}\right){c}_{\phi }{s}_{\phi }{c}_{\theta }& {I}_{xx}{s}_{\theta}^2+{I}_{yy}{s}_{\phi}^2{c}_{\theta}^2+{I}_{zz}{c}_{\phi}^2{c}_{\theta}^2\end{array}\right] $$

(10.20)

where the c matrix is the Coriolis term containing the gyroscope and centripetal terms (Herrera and Gómez 2015).

Now, Eq. (10.19) can be used to derive angular acceleration equations to get

$$ \ddot{H}={J}^{-1}\left({\tau}_B-C\left(H,\dot{H}\right)\dot{H}\right) $$

(10.21)

Then, calculate the inverse of J and substitute it in Eq. (10.21) to get the following angular acceleration equations of the quadcopter:

$$ \left.\begin{array}{c}\ddot{\phi}=\frac{I_y-{I}_z}{I_x}\dot{\theta}\dot{\psi }-\frac{J_{\mathrm{r}}}{I_x}{W}_r\dot{\theta}+\frac{U_2}{I_x}\\ {}\ddot{\theta}=\frac{I_z-{I}_x}{I_y}\dot{\phi}\dot{\psi }-\frac{J_r}{I_y}{W}_r\dot{\phi}+\frac{U_3}{I_y}\\ {}\ddot{\psi}=\frac{I_x-{I}_y}{I_z}\dot{\theta}\dot{\phi }+\frac{U_4}{I_z}\end{array}\ \right\} $$

(10.22)

where W_r is the algebraic sum of the angular speeds of motors:

$$ {W}_r=-{w}_1+{w}_2-{w}_3+{w}_4 $$

(10.23)

J_r is the inertia of the motor and is a very small value and often can be omitted so Eq. (10.22) and (10.24):

$$ \left.\begin{array}{c}\ddot{\phi}=\frac{I_y-{I}_z}{I_x}\dot{\theta}\dot{\psi }+\frac{U_2}{I_x}\\ {}\ddot{\theta}=\frac{I_z-{I}_x}{I_y}\dot{\phi}\dot{\psi }+\frac{U_3}{I_y}\\ {}\ddot{\psi}=\frac{I_x-{I}_y}{I_z}\dot{\theta}\dot{\phi }+\frac{U_4}{I_z}\end{array}\ \right\} $$

(10.24)

Equations (10.17) and (10.24) represent linear and angular motions of quadrotors. The mathematical model can be implemented in MATLAB/Simulink or another environment to perform the tests in multiple scenarios and additional purposes by researchers to achieve optimal performance (Armah et al. 2016).

Linear and angular velocity states can be calculated by integrating Eqs. (10.17) and (10.24), respectively; in turn, linear and angular position states can be calculated by double integration of Eqs. (10.17) and (10.24). The 12 states $\left(x,\dot{x},y,\dot{y},z,\dot{z},\phi, \dot{\phi},\theta, \dot{\theta},\psi, \dot{\psi}\right)$ are the required states for the control of the quadrotor. Some of these states can be measured by sensors, while others can be estimated by special “observers” such as KFs or extended Kalman filters (EKFs).

4 Control of Quadrotors

Every type of aircraft has actuators that are used to generate linear and angular forces which enable movement in different ways to achieve the desired position. As mentioned earlier, quadrotors use four motors (actuators) to generate forces but are unable to achieve desired positions without the use of control systems which generate appropriate control signals.

A flight controller is essentially a circuit board with sensors that relays variation in coordinates of the quadrotor. It may receive user commands and controls the rotor’s motors so as to retain the sought after position.

Most control systems reduce the error ratio between desired and sensor-measured signals to generate appropriate control signals for motors, until the quadrotor reaches the desired location where the error signal will be zero. Quadrotors require a highly nonlinear multivariable system that has strong coupling between translation and angular motion and hence are highly sensitive to external disturbances. Moreover, large payload variation may have noticeable effects. Accordingly, robust controller is needed to deal with sudden changes as well as provision of tracking performance in the presence of modeling error and uncertainties. The most commonly used types of controllers are as follows:

Proportional Integral Derivative (PID) Controllers

Different types of PID controllers are usually designed to reach a desired position. However, tuning methods are required to obtain suitable controller settings; for this purpose, Bouabdallah et al. (2004), Pounds et al. (2010), and Argentim et al. (2013) utilized integral time absolute error (ITAE) criteria. In Abbasi et al. (2013), a fuzzy self-tuned PID controller was proposed. Bergkvist (2013) implemented a PID controller for real-time “Android” operating systems. Sadeghzadeh et al. (2014) implemented single PID and gain scheduling-PID. Kader et al. (2014) proposed PID and compared it with fuzzy controllers for attitude and altitude signals. It is simple to design a PID; it provides good performance and requires minimal control effort. Wang et al. (2016) provided a robust cascade PID controller that alleviates disturbances, and Ferry (2017) designed a PID .

Optimal and Adaptive Controllers

Linear quadratic (LQ) control was applied by Bouabdallah et al. (2004), and a classic linear quadratic regulator (LQR) controller was utilized by Argentim et al. (2013); Araar and Aouf (2014) designed an LQ-servo controller that provides improved performance and attains robust trajectory design even in presence of gusts of wind. Moness and Bakr (2015) and Purnawan et al. (2017) introduced a further LQR controller design for quadrotors.

Adaptive Control

Adaptive control is an advanced control technique to maintain a desired level of control system performance, when the parameters of the plant dynamic model are unknown and/or change in time (Minh et al. 2014).

Nonlinear and Intelligent Controllers

Dikmen et al. (2009) applied different types of nonlinear controllers for quadrotor control systems including inverse dynamic control, feedback linearization control, and sliding mode control. Sliding mode (Thomas 2010; Balasubramanian and Vasantharaj 2013) applied computed torque control mechanism to nonlinear dynamics of a quadrotor with consideration of disturbance; in the latter, improved robustness is gained in the presence of small changes in the payload as compared to other techniques. Yacine et al. (2015) used a combination of a fuzzy logic control (FLC) and a sliding mode control (SMC) in order to improve performance of quadrotors. Sliding mode has been further advanced (Tripathi et al. 2016; Abdullah and Sabar 2015) establishing a fuzzy controller to regulate the height, roll, pitch, and yaw of the quadrotor using a genetic algorithm (GA). In addition, fuzzy control has been applied by Sattar and Ismail (2017).

5 Case Studies

5.1 Precise Positioning for Delivery Quadrotor

In this case study, the PID control algorithm will be applied to control the position of a quadrotor system. The block diagram used to calculate the PID is shown in Fig. 10.4. The PID is the part of the flight control software that receives the data from sensors and determines the necessary speed of the quadrotor’s motor. There are three parameters in a PID controller, the P, I, and D terms (Liang 2018):

• “P” tends to reduce the present error.

• “D” is a prediction of future errors – it helps to accelerate approaching a set-point and counteracts P when it is getting close to minimize overshoot.

• “I” is the accumulation of past errors ; it works on reducing the steady-state error by managing the forces that happen over time; for example, if a quad constantly drifts away from a set-point due to wind, it will spool motors up to counteract it.

Fig. 10.4

Block diagram of quadcopter control by PID control

The general formula of a PID controller (Fernando et al. 2013; Kotarski et al. 2016) can be written as

$$ PID(e)={k}_{\mathrm{p}}e(t)+{k}_{\mathrm{I}}\int_0^te\left(\tau \right) d\tau +{k}_{\mathrm{D}}\frac{d}{dt}\mathrm{state} $$

(10.25)

where e(t) = desired state(t) − measured state(t), k_p, k_I, and k_D are the proportional, integral, and derivative gains, respectively.

Altitude Control

Appropriate thrust force , U₁, is required to achieve the desired altitude and can be calculated by

$$ {U}_1={k}_{p_z}{e}_z+{k}_{I_z}\int {e}_z+{k}_{D_z}\frac{d}{dt}{e}_z+ mg $$

(10.26)

where ${k}_{p_z}$, ${k}_{I_z}$, and ${k}_{D_z}$ are the altitude PID gains controller; e_z is the altitude error e_z = z_des − z_meas, z_des and z_meas are desired and measured altitude, respectively; and g is the Earth gravity.

The roll control, pitch control, and yaw control Eqs. (10.27–10.29) are used to determine appropriate torques to achieve the desired attitude .

Roll Control

The following equation is used to determine appropriate torque (U₂) to rotate a quadrotor around the x-axis:

$$ {U}_2={k}_{p_{\phi }}{e}_{\phi }+{k}_{I_{\phi }}\int {e}_{\phi }+{k}_{D_{\phi }}\frac{d}{dt}{e}_{\phi } $$

(10.27)

where ${k}_{p_{\phi }}$, ${k}_{I_{\phi }}$, and ${k}_{D_{\phi }}$ are the roll angle PID gains controller; e_ϕ is the roll angle error; e_ϕ = ϕ_des − ϕ_meas; ϕ_des and ϕ_meas are the desired and measured roll angle , respectively.

Pitch Control

The torque (U₃) is required to rotate a quadrotor around the y-axis and can be calculated by

$$ {U}_3={k}_{p_{\theta }}{e}_{\theta }+{k}_{I_{\theta }}\int {e}_{\theta }+{k}_{D_{\theta }}\frac{d}{dt}{e}_{\theta } $$

(10.28)

where ${k}_{p_{\theta }}$, ${k}_{I_{\theta }}$, and ${k}_{D_{\theta }}$ are the pitch angle PID gains controller; e_θ is the pitch angle error e_θ = θ_des − θ_meas; θ_des and θ_meas are the desired and measured pitch angle , respectively.

Yaw Control

The torque (U₄) is needed to rotate a quadrotor around z-axis and can be properly calculated by

$$ {U}_4={k}_{p_{\psi }}{e}_{\psi }+{k}_{I_{\psi }}\int {e}_{\psi }+{k}_{D_{\psi }}\frac{d}{dt}{e}_{\psi } $$

(10.29)

where ${k}_{p_{\psi }}$, ${k}_{I_{\psi }}$, and ${k}_{D_{\psi }}$ are yaw angle PID gains controller; e_ψ is yaw angle error e_ψ = ψ_des − ψ_meas; ψ_des and ψ_meas are desired and measured yaw angle, respectively.

The current quadrotor model has six DOF and only four actuators (motors), so direct control of all DOF is complex. Meanwhile, the control Eqs. (10.26–10.29) are used to directly control four of the DOF (z, ϕ, θ, ψ). The roll and pitch angles move the quadrotor towards the desired x and y location. Consequently, the desired x and y will be used first to calculate the desired roll and pitch angles in order to control x and y positions indirectly. Meanwhile, the equations that are used to calculate desired roll and pitch angles are obtained in terms of desired x and y as Shahid et al. (2016):

$$ {\phi}_d={\tan}^{-1}\left(\frac{U_y\cos {\theta}_d}{g-U1}\right) $$

(10.30)

and

$$ {\theta}_d={\tan}^{-1}\left(\frac{U_x}{U1-g}\right) $$

(10.31)

where U_x and U_y are calculated as follows:

$$ {U}_x={k}_{p_x}{e}_x+{k}_{I_x}\int {e}_x+{k}_{D_x}\frac{d}{dt}{e}_x $$

(10.32)

$$ {U}_y={k}_{p_y}{e}_y+{k}_{I_y}\int {e}_y+{k}_{D_y}\frac{d}{dt}{e}_y $$

(10.33)

where e_x = x_des − x_meas is the error position in the direction of x-axis, x_des and x_meas are desired and measured position in the direction of x-axis, respectively. Further, e_y = y_des − y_meas is the error position in the direction of y-axis, y_des and y_meas are the desired and measured position in the direction of the y-axis, respectively.

There are two main control loops: inner and outer. The outer loop is used to calculate U₁, U_x, U_y, ϕ_d, and θ_d. The inner loop is used to calculate the desired control signals U₂, U₃, and U₄. Figure 10.5 shows the overall control block diagram of quadrotor. Control signals U₁, U₂, U₃, and U₄ are feed to the Electronic Speed Control (ESC) devices to generate appropriate electrical signal used to control the speed of each motor. The block diagram in Fig. 10.5 has been implemented by the technical computing platform Matlab. Figure 10.6a–e shows the simulation response of the states X, Y, Z, φ, and θ of the quadrotor under a PID controller for fixed position (x = 20, y = 15, z = 10, and ψ = 0).

Fig. 10.5

Control block diagram of quadrotor

Fig. 10.6

State simulation time response of quadrotor: (a) X-out response; (b) Y-out response; (c) Z response; (d) φ response; (e) θ response

5.2 Adaptive Positioning of Quadrotor

Multiple model adaptive control (MMAC) is a state feedback controller. This adaptive control implants its construction in a bank of filters as Kalman filters (KFs) . For the quadrotor, each KF is intended for an explicit value of payload variation. Then, accordingly, a set of LQ-servo state feedback controllers are designed for tracking reference trajectories. The integral term of the LQ-Servo can effectively eliminate the tracking error.

MMAC is applied here to meet stability and performance requirements in two situations: additive payload, which leads to performance degradation or instability, and fluctuating of the operating point. The appropriate control signal is correlated with the highest weighting signal in order to provide the required control action. The assigned weighting signals rely on two important elements: the residual and covariance matrices of the KFs . Note that each KF is designed for a model that corresponds to the known value of the uncertain parameter (Hassani et al. 2011; Hassani et al. 2009).

The MMAC comprises of (i) N weighting signal, P_N, that generated from a dynamic weighting signal generator and (ii) a bank of N continuous-time estimator, KF_N. Each estimator is intended for one of the selected adopted models. Each of these carefully chosen models belongs to the original set of the plant’s model (Fekri et al. 2006).

The uncertain parameters’ vector signifies the uncertainty in linear state model of the quadrotor dynamic system. These parameters tolerate the matrices that define the structure of the linear model. For flexible illustration, it is presumed that the uncertain parameter (a) can take only one value for each run.

The dynamic weights characterize the finest deduction of model that is most likely to be accurate. These weights are supposed be the characterized issue in multiple model algorithms, and they are usually evaluated online. The dynamic weighting is initially set to 1/N and fulfils the following condition:

$$ \left({P}_i(t)\right)\in \left(0,1\right)\kern0.49em \mathrm{For}\ i=1\dots N $$

(10.34)

The dynamic weights are produced by dynamic weighting signal generator (DWSG) which is denoted by the following differential equation:

$$ {\dot{P}}_i(t)=-\mu\ \left(1-\frac{\beta_i(t)\ {e}^{-{w}_i(t)}}{\sum_{j=1}^N{P}_j(t)\ {\beta}_j(t)\ {e}^{-{w}_j(t)}}\right)\ {P}_i(t) $$

(10.35)

where μ is a positive constant theoretically equals to one and the function β_i(t) is denoted by

$$ {\beta}_{\boldsymbol{i}}(t)=\frac{1}{\sqrt{\mathbf{\det}{\boldsymbol{S}}_{\boldsymbol{i}}\left(\boldsymbol{t}\right)}} $$

(10.36)

and w_i(t) is an error measuring function between the measurement states of the quadrotor and the estimated measurable states of each local estimator. It can be evaluated as follows:

$$ {\boldsymbol{w}}_{\boldsymbol{i}}(t)=\frac{\mathbf{1}}{\mathbf{2}}{\left\Vert \boldsymbol{z}(t)-{\hat{\boldsymbol{y}}}_{\boldsymbol{i}}(t)\right\Vert}_{\mathbf{2}}\ {\boldsymbol{S}}_{\boldsymbol{i}}^{-\mathbf{1}}(t) $$

(10.37)

$$ {\boldsymbol{S}}_{\boldsymbol{i}}=\boldsymbol{C}\ {\boldsymbol{s}}_{\boldsymbol{i}}\ {\boldsymbol{C}}^{\boldsymbol{T}}+{\boldsymbol{R}}_{\boldsymbol{i}} $$

(10.38)

where s_i(t) is a uniformly positive definite weighting matrix, described by

$$ {\left\Vert \boldsymbol{x}\right\Vert}_2\boldsymbol{S}=\left({\boldsymbol{x}}^{\boldsymbol{T}}\boldsymbol{S}\;\boldsymbol{x}\right)\hat{\mkern6mu} \left(1/2\right) $$

(10.39)

Each control signal is obtained from the product of the state estimation $KF\ {\hat{x}}_k\left(t|t\right),k=1,2,3,\dots N$ and the gain supplied by an optimal linear quadratic control, G_k, as

$$ {u}_k(t)=-{G}_k\ {\hat{x}}_k\left(t|t\right),k=1,2,3,\dots \dots N $$

(10.40)

The “global” control signal , which enters both the quadrotor system and the banks of KFs, is calculated by the probabilistic weighting of each local control signal (Hassani et al. 2009). Consequently, the mixing of state estimation and generated feedback control can be clearly noticed. Therefore, any estimation errors of the state will directly affect the local control signals. Accordingly, in the MMAC design, the identification system and the control system are not separated (Fekri et al. 2007).

The employed MMAC with three KFs is shown in Fig. 10.7. The (a) value equals 0, 0.3, and 0.8 kg for KF number 1, 2, and 3, respectively. The three KFs are run in parallel when the parameter (a) is allocated to the reference model. The three KFs are initialized with x_o = [2 0 3 0 − 10 0 0.2 0.3 0 0.05]^T values with the initial weighting signal uniformly distributed Po = 1/3 (Raafat and Mahmoud 2018). Figure 10.8 shows the progress with time for the conditional probabilities for the three KFs. The quadrotor system tracks the desired references in about 5 s. This demonstrates the capability of the MMAC of reasonably fast convergence.

Fig. 10.7

Block diagram of MMAC

Fig. 10.8

Time histories for probability when the uncertainty in mass of a reference model is 0.8Kg

Figure 10.9 shows the closed loop responses of MMAC using three KFs, where the model and filters start at the same initial point. Figure 10.9a shows the response of the linear position (x) by using MMAC, where (curve 1) represents the actual response from the model, the estimated signal is represented in (curve 2), and the reference signal is explained in (curve 3). Figure 10.9(a–e) also shows the tracking for y, z, roll, pitch, and yaw, respectively. In Fig. 10.9, the linear and angular positions track the references, and the adaptation of this algorithm can be seen clearly where the actual response follows the true value by adjusting its parameter (a). Accordingly, Fig. 10.10 demonstrates the performance of the MMAC controlled system to follow the applied references. That reflects the capability of the controller to select the correct control signal. The root mean square error (RMSE) is used as a performance index.

Fig. 10.9

A closed loop response of the reference model for (a) the linear position x; (b) the linear position y; (c) the linear position z; (d) the angular position roll; (e) the angular positions pitch and yaw

Fig. 10.10

RMSE of tracking design when the mass uncertainty at reference model = 0.8 kg for: (a) The linear position, (b) the angular position

Figure 10.11 demonstrates the capability of tracking with initial conditions of the reference model which are different from those of filters which have a value of x = [5 0 6 0 − 5 0.1 0 0.3 0.9 0]. The four motors in our example provide plenty of power for the rotors to climb rapidly. Each motor is designed for ‘aeroplanes’ weighing (280–400 g). For additive payload, we use a large motor that provides more thrust with the same size of propellers. These motors have larger output wattage which usually handles bigger loads sufficiently.

Fig. 10.11

A closed loop response of quadrotor controlled system using MMAC , with Kalman filters (KFs) starting at different initial points from that of the reference model: (a) the linear position x; (b) the linear position y; (c) the linear position z; (d) the angular position roll; (e) the angular position pitch and yaw

6 Conclusion and Future Applications

Different types of quadrotors are increasingly used for different applications. The type and application affects the design of the required controller. A high level of safety and reliability need to be assured for social and airspace applications. Accurate measurements are necessary for robust behavior of quadrotors. In order to achieve observability of all the states, it is necessary to use estimators of KFs or EKFs.

Quadrotor has been increasingly used for delivery owed to the low cost, efficiency, and speed of parcel carriage; it overcomes the flow, congestion of roads, and traffic lights. Another important point is the reduction of the pollution of the environment; no combustible fuel is used, and power is supplied via a rechargeable battery. Quadrotors are unobtrusive and may reach rugged areas where cars or other forms of carriage cannot.

In this chapter, two cases of designing a controller for quadrotors have been described. The first presents the development of a PID controller to solve impulse input signal and prevent the system from saturation as well, as well as operating with minimal power under a simple and efficient algorithm. The second case presents the design of MMAC, in which the reference position is effectively tracked. The robustness of the adaptive controller is demonstrated when different initial positions are used from the true initial condition of the quadrotor. The performance of the adaptive control has been evaluated using the RMSE index, demonstrating its robust potential application in resource flow, as part of efficient systematic management of the needs of increasing, potentially remote/variable demographic populations.