Dynamic Behaviour of Road Bridge Deck When a Truck Moves Along the Irregularities of the Road Profiles

Abstract

Bridge is the structure that is seen several dynamic loads unlike other structures. Ministry of Road Transport and Highways (MORTH) said that 10,876 people were killed due to potholes in the year 2015, which denotes the lack of proper maintenance of road pavements. When a vehicle moves along these surface irregularities, it not only causes uncomfortable to the passenger but also causes dynamic loads on the components like deck slab, bearings. Since the road surface irregularities like unevenness, potholes, etc., are unavoidable, we should understand the dynamic effect on the structure due to such undulations.

IRC-6, standard to find the loads and load combinations on the road bridges, doesn’t talk about the dynamic load induced by surface irregularities with respect to the different classes of road profile as per ISO: 8608. On the other hand, IRC-6 only gives provisions of static analysis in the case of the vertical dynamic effect produced by moving vehicles.

This study aims to generate road profiles having different degrees of unevenness as per ISO: 8608 and to propose a conservative method to find the vertical dynamic load on the bridge deck and its vertical response.

A bridge deck is modeled as a Single Degree of Freedom system and the vertical dynamic responses of the bridge deck are found by Newmark’s Beta Linear Acceleration Method.

It is found that the dynamic response, almost doubles when road profile quality changes from one class to the very next class.

G.R. Reddy—Retired Outstanding Scientist at Bhabha Atomic Research Center Mumbai.

1 Introduction

Pavement unevenness is generally defined as an expression of irregularities in the pavement surface. It is also known payment roughness. Pavement unevenness is the main excitation source of the vehicle-bridge interaction system. When a vehicle crosses the bridge, the bridge pavement unevenness causes vehicle vibration which not only leads to the uncomfortably to the passengers but also leads to the bridge vibration. Miyamoto et al. (2011); proposed a health monitoring of existing short-and medium span Reinforced/ Pre-stressed concrete bridges based on the vibration data collected from the sensors that attached to public bus and mid span of bridge. The experiment study shows that there is a linear relation between bridge response and the bus-wheel response, especially there is a similarity in the vertical vibrations of bus-wheel and bridge deck when the vehicle reaches at mid-span which is an experimental validation of vehicle-structure interaction.

Wang et al. (2014); conducted field experimental study on the effect of traffic induced vertical vibration of the bridge deck on the fresh concrete during repair work of the bridge deck. During the study, the traffic induced vibration is stimulated by using an electromagnetic test stand and concluded that around 10% reductions in the compressive strength of high performance concrete before hardening and insignificant effect after hardening. The input simple harmonic loads of frequency ranges from 2.5 to 5.5 Hz, and the vertical deflection ranges from 0.3 to 3 mm are used for the studies. However the actual frequency contents of road induced vibration will be in the range of 1 to 20 Hz (Manning 1986).

By investigating 224 different types of bridges, the Swiss Federal Research Laboratory determined that a bridge’s actual measured natural frequency was ranges from 1.23 to 14 Hz with an average natural frequency of =3.62 Hz (Cheng 2003). To avoid amplification of response of the bridge deck, the frequency contents of the road unevenness induced dynamic load should not coincide with natural frequency of the bridge. Therefore, it is necessary to find out the frequency contents of such vibrations in order to find out its effect on the bridge deck and to propose suitable remedial measures in case the effect is considerably high.

The road unevenness induced dynamic load and the vibration response act in the vertical direction on the bridge deck. Since the pavement unevenness is unavoidable in road profile, on other hand one can’t construct a completely smooth road profile, it is very important to consider the dynamic behavior of the bridge deck subjected to road unevenness induced vibration because of the high sensitivity of human beings to the vibration. Human body has the ability to sense even small vibrations which are generally not capable of causing damage to the hardened concrete. Therefore, serviceability limits for the vibrations are based on the pedestrians comfort on the bridge deck. A peak velocity that ranges from 10 mm/s to 15 mm/s is considered as unpleasant and unacceptable to the pedestrians on the bridge deck (Wiss et al. 1974); and (Manning 1986).

Apart from the inherent unevenness, further damages in the pavement like potholes make the road profile even worst as shown in the Fig. 1.

Fig. 1.

Bridge deck having irregular road profile.

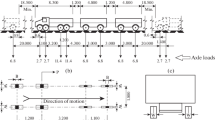
Such scenarios became common in the Indian roads. Ministry of Road Transport and Highways (MORTH) report on data of road accidents in India shows that an average 10,000 people were killed due to potholes in the year 2015, 2014 and 2013. In 2016, 6,424 road accidents are reported as a result 2,324 people killed (Naveen et al. 2018). The accidents reasons may be due to the maintaining the design speed of highway or respective road when vehicle forced to move through these surface irregularities. So that the dynamic effect on the bridge deck slab with constant vehicle speed (i.e.: 36 km/h) and having vehicle of mass of 30tonnes moving along a standardized surface irregularities is studied.

Indian Roads Congress (IRC-6) the code which is used to find out the loads for design of bridges gives provision for impact of moving vehicle by a factor called ‘impact allowance’. Impact allowance is expressed as a percentage of the applied live load. The Impact allowance is different for different classes of vehicles such as wheeled loads and tracked loads.

Impact allowance or Impact factor for Class A or B wheel loading can be found by following expression given by IRC-6, Clause: 208.2.

$$ Impact\;factor = \frac{4.5}{{6 + L}} $$

(1)

where, ‘L’ is the span of the bridge in meters.

However, this code doesn’t talk about the dynamic load induced by different surface irregularities or the impact factor is a function of span of the bridge only. On the hand IRC-6 only gives provisions of static analysis in the case of vertical dynamic effect produced by moving vehicle.

The quality of a road profile can be assessed according to the ISO: 8608-Road surface profiles. According to the standards, surface irregularities road profiles can be classified into class A, B, C, D, E, F, G and H. As we move from class A to class H road surface irregularities increases on the other hand road profile quality decreases.

Wang et al. (2017); generated class-A road profile for a 40-m long bridge as per ISO: 8608 for the study of vehicle parameter identification based on the response of the bridge, which is then used as excitation in the simulation studies. The sampling interval of the generation of road class-A profile was set to 0.05 m, resulting in a sampling frequency of 20cycles/m, and 800 numbers of data points are is used to generate road profiles.

Bin Yu et al. (2019); studied the influence of road irregularities on ride comfort of mini vehicles. Road surface unevenness data is collected using road unevenness measuring instrument mounted on the test vehicle. The measurement and road profile reporting of the ground are carried out according to ISO 8608. The paper states that most of road profile quality will not go beyond Class – D. On the hand road profile classes beyond D represent off-road.

During the literature survey no article found that gives frequency contents and amplitudes of road unevenness vibration corresponding to different degrees of unevenness as per ISO: 8608. Several Experimental studies are conducted in order to find out the response of the bridge deck subjected to traffic induced vibration. However few drawbacks of experimental studies include expensive and time consuming and it is necessary to measure the degree of the unevenness in order to correlate with the experimental results. And no articles found which deal with the analytical study in order to predict the response of the bridge deck subjected to road unevenness induced vibration.

Since every paved road profiles will fall in the Class-A, or B, or C or in the worst condition class-D, this article aims to find the road induced dynamic load and the dynamic behavior of the bridge deck corresponding to each classes of possible road profiles. This article gives an idea to predict the dynamic response of the bridge deck having a less maintained road pavement. This will help in taking a decision regarding design and retrofitting of the bridge deck in the point of view of unevenness induced vibrations without measuring the road unevenness using an instrument.

This article also aims to provide Fourier amplitude spectrum which contains amplitudes and frequencies of road unevenness induced vibration corresponding to different degrees of possible unevenness on the bridge deck. This gives a proper input to the fatigue study of the bridge deck subjected to the road induced vibrations and to the study of vertical vibration on the fresh concrete that placed during repair and rehabilitation work which is the main reason behind the decision of controlling the traffic during the work.

This article also proposes a simplified model of bridge of Single Degree of Freedom system, and the vertical dynamic responses of the bridge deck are found by Newmark’s Beta Linear Acceleration Method.

2 Generation of Road Profiles of Class-A, B, C and D as PER ISO: 8601

The first step to find the road unevenness induced dynamic load, is the generation of road profiles having different degrees of unevenness. The ISO: 8608 gives the data for the generation of different classes of road profile based on the degrees of unevenness.

Wang et al. (2014); state that, according to the road classification map, it is known that most the paved roads are belong to road class-C and only low-frequency sections extend to road class-D. Thus the generation of road profiles is limited to class-D.

When a bridge contains road profiles having more irregularities (say class-C), the dynamic load that induced by moving vehicle also will be more. This paper attempts to quantify the dynamic load and its effect on the bridge deck by generating different classes of the road profiles in the simply supported bridge having main span length of 36.58 m (120 ft) shown in the Fig. 2.

The other properties of the bridge are listed below.

• a) Cross sectional area of the deck (superstructure) (A) = 6.36 m².

• b) Second Moment of area about longitudinal direction of bridge I_xx = 2.061 m⁴;

• c) Second Moment of area about transverse direction of bridge I_yy = 87.87 m⁴;

• d) Modulus of elasticity material (E_c) = 20,700 MPa

• e) Material density ρ = 2,400 kg/m³

• f) length of column L_c = 6.10 m (20 ft)

• g) Diameter of column (D) = 2.74 m (9 ft).

Fig. 2.

Simply supported box girder bridge.

Let ‘L’ be the Main span length of the bridge = 36.58 m (120 ft) and take number of data points (N) = 800.Therefore, the sampling interval of the pavement unevenness (dx) = L/N = 0.0457 m. On the other hand the distance along the bridge length (x) varies from 0 m to 36.58 m with an interval (dx) of 0.0457 m.

The spatial frequency range is fixed as per ISO: 8608 clause 5.1.1.5. According to that minimum spatial frequency is 0.01 cycles/m for on-road vehicles. The maximum spatial frequency is fixed as per ISO: 8608 Annexure-C. According to that for 70 km/h vehicle speed, maximum spatial frequency is given as 1.414 cycles/m. As the vehicle speed decreases higher maximum frequency is adopted. Therefore, 2 cycles/m is taken as the maximum spatial frequency for 36 km/h vehicle speed. Linear variation of spatial frequency is adopted in between minimum & maximum spatial frequency. So that variation in spatial frequency ($\Delta \mathrm{n}$) is taken as,

$$\left(\Delta n\right)=\frac{maximum\,spatial\,frequency }{N}=0.0025\;cycles/m$$

(2)

On the other hand spatial frequency varies from 0.01cycles/m to 2 cycles/m with an interval of 0.0025 cycles/m.

According to ISO: 8608, road profile $\mathrm{y}\left(\mathrm{x}\right)$ is given by

$$y\left(x\right)={\sum }_{i=1}^{N}\sqrt{2G({n}_{i})\Delta n}\times c\mathit{os}(2\pi {n}_{i}x+\emptyset)$$

(3)

Where,

$$G\left({n}_{i}\right)=G\left({n}_{o}\right)\times ({\frac{{n}_{o}}{{n}_{i}}) }^{2}$$

(4)

${\mathrm{n}}_{\mathrm{o}}=0.1\frac{\mathrm{cycles}}{\mathrm{m}}$ (Recommended by ISO: 8608), ${\mathrm{n}}_{\mathrm{i}}$ is the spatial frequency at ${\mathrm{i}}^{\mathrm{th}}$ point ‘${\emptyset}$’ is the random phase angle varies from $0\,\mathrm{ to}\,2\uppi$ and $\mathrm{G}\left({\mathrm{n}}_{\mathrm{o}}\right)$ is the displacement power spectral density and its value for different classes of road profiles is given for ${\mathrm{n}}_{\mathrm{o}}=0.1$ cycles/min the Table 1.

Table 1. Displacement power spectral density $\mathrm{G}\left({\mathrm{n}}_{\mathrm{o}}\right),$ for different classes of road profile as per ISO; 8608

It is worth of noting that,

• a) While generating the road profiles for different classes for a given bridge, only $\mathrm{G}\left({\mathrm{n}}_{\mathrm{o}}\right)$ is changing, rest of the parameters are same as explained above.

• b) The road profile generated using the Eq. 3 will not be exactly same all the time. It is because of randomness in the phase angle ($\varphi$) in the equation. However the peaks of vertical profile generated for a particular class will be close all the time.

• c) For the same reason the induced dynamic load which is derived from the vertical profile generated (explained in the coming section) also will not be exactly same all the time. However the peaks of vertical dynamic load induced and response of the bridge for a particular class will be close all the time.

With the help of MATLAB programme, different road profiles are generated as per above equations and parameters and shown below.

For road class-A (Figs. 3 and 4),

Fig. 3.

Class-A road profile.

Fig. 4.

PSD in spatial domain for Class-A road profile.

For road class-B (Figs. 5 and 6),

Fig. 5.

Class-B road profile.

Fig. 6.

PSD in spatial domain for Class-B road profile.

For road class-C (Figs. 7, 8 and 9),

Fig. 7.

Class-C road profile.

Fig. 8.

PSD in spatial domain for Class-C road profile.

Fig. 9.

Class-D road profile.

Since the Power spectral density (PSD) in spatial domain, that is G(n) v/s n plot for each road profile matches with the ISO: 8608 ranges, the generated road profiles are acceptable.

For the pavement having quality of road class-D shows a unevenness peak of 0.1 m, such quality of pavements on the bridges is unrealistic. Therefore, we can limit the dynamic analysis up to road class – C. Most of the pavements on the bridges fall in the road class – A and B, in the cases of more potholes then it will fall in the worst class category, class-C.

3 Vehicle Characteristics and Induced Dynamic Load Calculation

When the truck moves through the bridge road having the surface irregularities as shown in the Fig. 10, it not only causes uncomfortable to the passenger but also causes dynamic loads on the components on the like, deck slab, bearings etc., Since road unevenness is unavoidable, we should consider the dynamic load on the structure due to such undulations. Unfortunately the Indian design codes for bridges (IRC-6) don’t give a procedure to quantify such dynamic loads with respect to different degrees of unevenness. This paper aims to demonstrate a procedure to find out the induced dynamic load on the bridge deck and the response of the bridge deck subjected to this particular load alone.

Fig. 10.

Representative figure of truck moving along the road surface irregularities.

Let us consider a truck of mass 30 tonnes moving with a speed (v) of 36 km/h (10 m/s). Therefore, Time required to cross the bridge (T) = $\frac{\mathrm{span}}{\mathrm{v}}=\frac{36.58}{10}$  = 3.568 s.

Let ‘x’ be the distance along the bridge and y(x) be the vertical profile. From the Sect. 2.1, we have the sampling interval along the span ‘dx’ = 0.0457 m. On the other hand x_i+1 − x_i = 0.0457 m.

Hence the time interval ($\Delta \mathrm{t}$) to cover adjacent data points (ie: vertical profile y(x)) is given by

$$\Delta t=\frac{dx}{v}=\frac{ 0.0457}{10}=0.0046\,\mathrm{s}$$

On other hand vehicle take $0.0046\,\mathrm{ s}$ to reach ${\mathrm{y}}_{\mathrm{t}(\mathrm{i}+1)}$ from ${\mathrm{y}}_{\mathrm{t}(\mathrm{i})}$.

Where, ${\mathrm{y}}_{\mathrm{t}(\mathrm{i})}$ & ${\mathrm{y}}_{\mathrm{t}(\mathrm{i}+1)}$ are adjacent values of vertical profile y(x).

There for velocity induced (${V}_{t(i)}$) by vehicle to deck is

$${V}_{t(i)}=\frac{{y}_{t(i+1)}- {y}_{t(i)}}{\Delta t}\mathrm{ m}/\mathrm{s}$$

(5)

And acceleration induced (${a}_{t(i)}$) by vehicle to deck is

$${a}_{t(i)}=\frac{{V}_{t(i+1)}- {V}_{t(i)}}{\Delta t}\mathrm{ m}/{\mathrm{s}}^{2}$$

(6)

So that the vertical dynamic force ($\mathrm{f}(\mathrm{t})$) induced by vehicle on the deck slab is given by

$${f(t) = M}_{v}\times {a}_{t(i)}$$

(7)

Matlab Programme is generated for above equations to find out the a(t) & $\mathrm{f}(\mathrm{t})$ for different road class profiles, and it is shown below.

For road class-A (Figs. 11 and 12),

Fig. 11.

Acceleration a(t) induced due to Class-A road profile.

Fig. 12.

Dynamic load f(t) induced due to Class-A road profile.

The amplitude Fourier’s spectrum for input acceleration a(t) is plotted to find the frequency content.

We have the time (T) required by the vehicle to cross the bridge of length 36.58 m with velocity 10 m/s is 3.658 s. Since the maximum spatial frequency limited to 2 cycles/m. Total number of cycles = $2\times 36.58=73.16\;cyles.$ Therefore maximum frequency (${F}_{m}$) is given by,

$${F}_{m}=\frac{73.16\,cyles}{T}= 20\;{\rm Hz}.$$

(8)

It also can be found using the equation,

$$f = n\times v$$

(9)

Where, ‘n’ is the spatial frequency in cycles/m and ‘f’ is the time frequency in Hz.

$$\mathrm{f }=\mathrm{ n}\times \mathrm{v}=2\times 10=20\,\mathrm{ Hz}$$

The amplitude Fourier’s spectrum & frequency content is sensitive to velocity of the vehicle. The amplitude Fourier’s spectrum for input acceleration a(t) for 10 m/s for the given bridge length is shown in the Fig. 13.

Fig. 13.

Amplitude Fourier’s spectrum for Class-A road profile.

For road class-B (Fig. 14, 15 and 16),

Fig. 14.

Acceleration a(t) induced due to Class-B road profile.

Fig. 15.

Dynamic load f(t) induced due to Class-B road profile.

Fig. 16.

Amplitude Fourier’s spectrum for Class-B road profile.

For road class-C (Figs. 17, 18 and 19),

Fig. 17.

Acceleration a(t) induced due to Class-C road profile.

Fig. 18.

Dynamic load f(t) induced due to Class-C road profile.

Fig. 19.

Amplitude Fourier’s spectrum for Class-C road profile.

4 Dynamic Responses of the Bridge Deck Subjected to Induced Dynamic Load

The first step to find the dynamic response of the simply supported bridge deck, is modelling the deck slab. Since the given simply supported bridge deck slab acts as a beam with continuously distributed mass, we can idealize it into a single degree of freedom system in which 50% of dead load and full truck load are lumped at the mid span of the deck. This is appropriate conservative approach because; that we know that 50% of total distributed mass will participate in the 1^stmode of vibration of a simply supported beam as explained below.

Free vibration equation for beams having distributed mass and elasticity with negligible damping is given by

$$EI \frac{{\partial }^{4}y}{\partial {x}^{4}}+ \overline{m}\frac{{\partial }^{2}y}{\partial {t}^{2}}=0$$

(10)

Mode shape of n^th mode for uniform simply supported beam is given by

$${\emptyset}_{n}= \mathit{sin}\frac{n\pi x}{L}$$

(11)

Where n is the mode number and $\overline{\mathrm{m}}$ is the mass per unit length.

For first mode (ie: n = 1), Mode shape is given by

${\emptyset}_{1}(\mathrm{x})=\mathrm{ sin}\frac{\mathrm{\pi x}}{\mathrm{L}}$. As given in the Fig. 20(b)

And modal mass of nth mode is given by

$${M}_{n}= \int\nolimits_{0}^{L} {\overline{m}{{\emptyset }_{n}}^{2}\left(x\right)dx}$$

(12)

And Modal mass for 1st mode is given by

$${M}_{1}= \int\nolimits_{0}^{L} {\overline{m}{{\emptyset }_{1}}^{2}\left(x\right)dx}$$

(13)

$${\mathrm{M}}_{1}= \int\nolimits_{0}^{L} {\overline{\mathrm{m}}{(\mathrm{sin}\frac{{\uppi{\rm x}}}{\mathrm{L}})}^{2}\mathrm{ dx}= \frac{\overline{\mathrm{m}}\mathrm{ L}}{2}}$$

$${M}_{1}= \frac{\overline{m} L}{2} = \frac{M}{2}$$

(14)

It denotes that, for 1st mode modal mass is equals to 50% of total distributed mass.

Fig. 20.

(a) simply supported beam with distributed mass property. (b) 1^st mode shape.

4.1 Bridge Deck Slab Model for Vertical Vibration

As explained earlier we can idealize bridge deck into a single degree of freedom system in which 50% of dead load and full truck load are lumped at the mid span of the deck. Apart from this following assumptions are also applied in modelling and response calculation.

4.1.1 Assumptions

• a) The dead load is taken as mass of main span deck slab only and it is given by

  $$ AL_{s} \rho = 6.36\;{\text{m}}^{2} \, \times \,36.58\;{\text{m}}\, \times \,2,400\,{\text{kg}}/{\text{m}}^{3} \; = \;558357\,{\text{kg}} $$

• b) The live load is taken mass of truck 30,000 kg. However Dead load and Live load should be considered as per IRC – 6 loads and load combinations for design and analysis of bridge as per Indian standards.

• c) Lumped mass method is performed to get dynamic response of bridge deck slab, in which 50% of dead load together with full live load is considered as lumped mass.

  Thus Lumped mass (M) = (0.5 $\times$ 558357 + 30000) = 309179 kg and this mass M is lumped at the centre of span as shown in the Fig. 21(a).

• d) Damping of the structure is 5%

• e) To simplify the problem, the bridge is assumed to move only in the direction of dynamic load (vertical direction) at the centre of bridge. On the other hand structure has only one degree of freedom and the dynamic load f (t) induced by the truck when it moves along the unevenness is assumed as acting at the centre of span where mass is lumped, as shown in the Fig. 21.

  Fig. 21.

  

  (a) simply supported beam with lumped mass at center. (b) SDOF model.

• f) There for Stiffness of bridge deck (K)

  $$K=\frac{48\,E\,Ixx}{{L}^{3}}=\frac{48\times 20700\times {10}^{6}\times 2.061}{{36.58}^{3}}=41.837\times {10}^{6}\,{\rm N/m}$$

  (15)

• g) Mathematical model of SDOF system is shown in the Fig. 21(b).

• h) Where, M = 309179 kg (as per section f), K = $41.837\times {10}^{6}\,\mathrm{ N}/\mathrm{m}$ &

  Natural circular frequency (${\omega }_{n}$) of SDOF system of bridge deck is given by

  $${\omega }_{n}=\sqrt{\frac{K}{M}} =\sqrt{\frac{41.837\times {10}^{6}}{309179}=11.63\,{\rm rad/s}}$$

  (16)

  Or natural time period $\left({\mathrm{T}}_{\mathrm{n}}\right)=\frac{2\uppi }{{\upomega }_{\mathrm{n}}}=0.54\,\mathrm{s}$.

  Or Natural frequency $({\mathrm{f}}_{\mathrm{n}})=\frac{1}{{\mathrm{T}}_{\mathrm{n}}}=1.85\,\mathrm{ Hz}$.

4.2 Vertical Dynamic Responses of the Bridge Deck Model Using Newmark’s Beta Method

The Newmark-β Method includes, in its formulation, several time-step methods used for the solution of linear or nonlinear equations. It uses a numerical parameter designated as β. The method, as originally proposed by Newmark (1959), contained in addition to β, a second parameter γ. Particular numerical values for these parameters leads to well-known methods for the solution of the differential equation of motion, the constant acceleration method, and the linear acceleration method.

The Linear acceleration method is more accurate than average acceleration method. So that $\upgamma =\frac{1}{2},\upbeta =\frac{1}{6},\mathrm{where}\,\gamma\,\&\,\beta$ are Newmark’s parameters.

The equation of motion at any time instant ${\mathrm{t}}_{\mathrm{i}}$ is given by,

$${M\ddot{x}}_{i}+C{\dot{x}}_{i} +K{x}_{i}=F({t}_{i})$$

(17)

According to Newmark’s beta method incremental responses is given by,

$${\Delta x}_{i}=\frac{{\widehat{\Delta F}}_{i}}{\widehat{k}}$$

(18)

$${\Delta \dot{x}}_{i}=\frac{\gamma }{\beta \Delta t}{\Delta x}_{i}-\frac{\gamma }{\beta }{\dot{x}}_{i}-\Delta t\left(\frac{\gamma }{2\beta }-1\right){\ddot{x}}_{i}$$

(19)

$${\Delta \ddot{x}}_{i}=\frac{1}{\beta {(\Delta t)}^{2}}{\Delta x}_{i} -\frac{\gamma }{\beta \Delta t}{\dot{x}}_{i} -\frac{1}{2\beta }{\ddot{x}}_{i}$$

(20)

There for, response at ${\mathrm{t}}_{\mathrm{i}+1}$ time instant is given by,

$${\ddot{x}}_{i+1}={\ddot{x}}_{i}+{\Delta \ddot{x}}_{i}$$

(21)

$${\dot{x}}_{i+1}={\dot{x}}_{i}+{\Delta \dot{x}}_{i}$$

(22)

$${x}_{i+1}={x}_{i}+{\Delta x}_{i}$$

(23)

4.2.1 Input Parameters for Newmark’s Beta Method

The following input parameters are considered for the numerical integration using Newmark’s Beta Method. Also checks for the time period and stability are done.

• a) $\gamma =\frac{1}{2}, \beta =\frac{1}{6}$

• b) Initial displacement (${x}_{o}$) = 0, Initial velocity (${\dot{x}}_{o}$) = 0

• c) M = 309179 kg, K = $41.837\times {10}^{6}\,{\rm N/m}$ & Damping ratio ξ = 0.05.

• d) Time step ($\Delta \mathrm{t}$) = 0.005 s

  Check for time step

  • i) $\Delta \mathrm{t}$ < $\frac{{\mathrm{T}}_{\mathrm{n}}}{10}$ is the natural time period = 0.54 s.

    0.005 < $\frac{0.54}{10}$, Hence ok.

  • ii) Stability check,

    $$\frac{\Delta t}{{T}_{n}}\le \frac{1}{\pi \sqrt{2}} \frac{1}{\sqrt{\gamma -2\beta }}$$

    (24)

    $\frac{0.005}{0.54}=0.0093 <0.55$ Hence ok.

4.3 Vertical Dynamic Responses of the Bridge Deck at the Mid Span Location

The MATLAB program for the Newmark’s Beta Method is generated and the parameters mentioned in the Sect. 4.2.1 are given as input and responses are obtained corresponding to different classes of road profiles which are shown below (Figs. 22, 23, 24, 25, 26 and 27).

Fig. 22.

Displacement response of bridge deck due to Class-A road profile.

Fig. 23.

Velocity & acceleration response of bridge deck due to Class-A road profile.

Fig. 24.

Displacement response of bridge deck due to Class-B road profile.

Fig. 25.

Velocity & acceleration response of bridge deck due to Class-B road profile.

Fig. 26.

Displacement response of bridge deck due to Class-C road profile.

Fig. 27.

Velocity & acceleration response of bridge deck due to Class-C road profile.

5 Comparison of Results of Class-A, B, C and D Road Profiles

The Table 2 shows comparison study of dynamic responses due to different classes of road surface profiles on the bridge deck. From the table it is evident that as we move from one road surface profile to very next road profile, peaks of responses almost doubles.

Table 2. Comparison study of dynamic response due to different classes of road profiles

Cassaooly et al. (1972) gives the vertical deflection time history of bridge deck based on the experimental study conducted on the five span continuous bridge when the test vehicle crosses the bridge. The defection is measured at the mid span location of third span having 24 m. The maximum response is nearly 6 mm and road class category is not mentioned. However, on comparing the displacement response obtained based on the analytical study conducted in this article with the experimental result, one can conclude that the model that proposed is reasonably good because the model discussed in this article has the natural frequency 1.85 Hz which is well away from the major frequency contents of the unevenness induced dynamic load, whereas the bridge deck discussed by Cassaooly et al. (1972) has a natural frequency 3.7 Hz which little more closer to frequency contents of the excitation. Hence the displacement response obtained in the experimental study is slightly higher than analytical study results as mentioned in the Table 2.

6 Conclusions

The Indian IRC-6, the European code EN: 1991 and the American code AASHTO which are used for designing the bridge structures don’t give provisions for dynamic analysis for unevenness induced dynamic load on the bridge deck.

A mathematical model of the bridge deck is proposed in this article in which the bridge deck is approximated to a single degree of freedom system having 50% of dead load and full vehicle mass is lumped at the centre of deck which is a conservative and simple approach. The proposed model can be used to find the response of the bridge deck subjected to the unevenness induced dynamic load, since the model shows reasonably good agreement with the experimental study conducted by Cassaooly et al. (1972).

The results of the analytical study conducted in this article can be used to predict the dynamic response of the bridge deck having less maintained pavement subjected to the unevenness induced vibration without measuring the degree of unevenness.

The frequency contents of the unevenness induced vibration ranges from 1 Hz to 20 Hz. However, the amplitude of the dynamic excitation is high in the range of 5 Hz to 20 Hz Although the unevenness induced dynamic load alone is not sufficient to make any immediate damage in the hardened concrete, since the unevenness induced load is a normally occurring cyclic load the fatigue study of the concrete should be conducted. The results obtained in this article can be used as an input for such studies.

As degree of the unevenness increases the velocity response also increases and sufficient enough to make discomfort to the pedestrians on the bridge deck, since the velocity response is beyond the limits mentioned by Wiss et al. (1974) and Manning (1986).