Robust Control Design of MIMO Systems

Abstract

A solution for designing the controllers in the case of systems with uncertainty is offered by the robust control theory, which can be generalized to MIMO (multiple-input multiple-output) systems. Some principles of the design methodologies of the robust controllers based on H2 and H-infinity synthesis are presented in this paper and applied on a multiple-input multiple-output system to achieve good performances and stability in the presence of modeling errors. For this purpose, the SISO (single-input single-output) closed-loop control diagrams are first adapted to MIMO systems. The study case used in the paper consists of the typical example of two-coupled tanks process which has two inputs and two outputs. The plant mathematical model includes also the possible additive uncertainty of the hydraulic resistances of the outlet and cross-coupling valves. The design of the H2 and H-infinity controllers and the study of the behaviors of the global systems were made in the Matlab environment using the Robust Control Toolbox.

1 Introduction

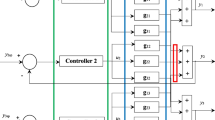
Conventional controllers (e.g. PID proportional-integrative-derivative controllers) are often used in the industrial control of the SISO plants. These controllers have a known structure and setup, are flexible, and easier to be implemented. Several issues should be considered in the case of MIMO plants in comparison to SISO systems because of the additional inputs and outputs: the performances and evolution for each output, the interaction between the variables, the compensations of the disturbances, and uncertainty. All the design methodologies based on the closed-loop system from Fig. 1 include the transfer matrix of the plant H_P(s) and the transfer matrix of the controller H_C(s).

There is a continuous concern among researchers and industrial applications when control structures H_C(s) should achieve the desired performances for the MIMO systems.

The QFT (Quantitative Feedback Theory) is a technique presented in [1] and could be used first to decompose the MIMO plant in several MISO (Multiple-Input-Single-Output) systems and design the controllers and filters which assures the robust performances for the systems containing uncertainty.

Fig. 1.

The general closed-loop control diagram for MIMO systems.

Aspects of control law synthesis for a linear MIMO process are described in [2] considering the quantized output and external disturbances. The determined controller assures a reference tracking accuracy which depends on the quantization.

The control problem of MIMO systems with different time delays often found in the industrial applications is addressed in [3]. The authors propose a solution with multiple-loops control to reinforce the tracking performances and controller robustness in case of uncertainty and disturbances. The disturbance rejection and robust stability are assessed with frequency performance indicators.

Several robust control methods are tested on the quadruple tank process in [4]. The MIMO controller is designed based on H2 and H-infinity synthesis for the linearized system with uncertainty.

The robust control strategy is also applied in [5] to achieve the desired response with required performances and disturbance rejection. The synthesis method is based on multi-objective optimization used for systems with uncertainty. The authors tested the method using two processes, including the two-coupled tanks process.

A robust controller that satisfies the H-infinity criterion in the frequency domain is developed in [6] for LTI (linear time‐invariant) single‐input single‐output systems. The design method uses fixed‐order controllers and the necessary and sufficient conditions for the existence of such controllers are described by a set of convex constraints.

In [7] the identification of the MIMO active magnetic bearing (AMB) system shows an unstable open-loop behavior because the system has two poles in the right-half of the complex plane and the authors use the H2 and H-infinity approaches to obtain the MIMO controller. The cross-interaction channels have negligible gains in the low-frequency region, and in this way, the system is almost decoupled (diagonalized).

The case of nonlinear MIMO systems is treated in the presence of unknown disturbances in [8]. The backstepping technique and the dynamic surface method are used to design the robust controller for a UAV (unmanned aerial vehicle).

The robust control problem of MIMO systems, H-infinity norm, sensitivity functions, performance requirements, mixed sensitivity problem, and robustness analysis are well described in [9]. Authors of [10] include also in their study the robustness of the systems with uncertainty, the choice of the weighting functions, and the H2, H-infinity and loop-shaping synthesis.

The mathematical modeling of the two-coupled tanks process which has two inputs and two outputs is presented in [11]. For the MIMO system was designed and tested a robust control algorithm based on H-infinity loop-shaping method.

Considering the sensitivity functions, the performance requirements include the desired shape for the sensitivity function in the frequency domain, the maximum amplitude, the bandwidth, and the tracking error. The study of the effect of these parameters on the weighting functions and systems performances is realized in [12].

The textbook [13] is a good introduction to the automatic control theory, contains aspects of mathematical modeling, conventional control, LQG (Linear Quadratic Gaussian) control, and also robust control design using H2 and H-infinity technique.

In [14] different types of conventional or robust control structures are determined and the behavior of the control schemes in time or frequency domain is simulated using the Matlab environment and its toolboxes.

The present paper proposes a short analysis of a MIMO system based on simulation of the behavior of the two-coupled tanks control system. In the design stage, robust control methods are used. In this sense, Sect. 2 presents the general diagram of the system with uncertainty and control diagrams used for determining the robust controllers. In Sect. 3 are detailed the control design aspects using the H2 and H-infinity synthesis. These aspects and the Matlab environment are used in Sect. 4 to obtain the robust controllers for the MIMO process. Section 5 emphasizes some conclusions regarding the robust control design of the two-coupled tanks process.

2 MIMO Systems with Uncertainty. The Weighting Matrix

The mathematical models should contain the dynamic behavior of the systems, but also information about the disturbances. The modeling procedure of the physical systems involves a compromise between simplicity and accuracy. So, some of the components are neglected to obtain a usable model, and differences from the real system are included in the modeling errors. These modeling errors should be considered somehow in the analysis and design of the automatic control as uncertainty based on available information and reasonable assumptions.

Figure 2 shows the closed-loop control diagram of the system with additive/multiplicative (unstructured) uncertainty [9, 10, 13].

Fig. 2.

The closed-loop control diagram of a system with unstructured uncertainty.

The transfer function of the system with uncertainty is

$$ H_{G} \left( s \right) = \Delta_{A} \left( s \right) + H_{P} \left( s \right)\left[ {I + \Delta_{M} \left( s \right)} \right]. $$

(1)

In (1) if $\Delta_{A} \left( s \right) = 0$ the relation emphasizes the multiplicative uncertainty and for $\Delta_{M} \left( s \right) = 0$ relation contains the additive uncertainty.

Determination of the control structure based on robust synthesis techniques depends on the weighting functions for the SISO case and the weighting matrix for the MIMO case (Fig. 3).

Fig. 3.

The robust control diagram for the MIMO system including the weighting matrix.

Once the weighting matrix is known, then the H-infinity design problem can be addressed for the augmented system and the output vector is [9, 10, 13].

$$ Y\left( s \right) = \left[ {\begin{array}{*{20}c} {Y_{e} \left( s \right)} & {Y_{u} \left( s \right)} & {Y_{y} \left( s \right)} \\ \end{array} } \right]^{T} . $$

(2)

Fig. 4.

Robust control diagram with the augmented plant model

The robust control design consists of:

• modeling the plant transfer matrix, H_P(s);

• choosing the weighting matrix, W_e(s), W_u(s), W_y(s) penalizing the error signal, control signal, and output signal, respectively;

• developing the augmented system, H_G(s) (see Fig. 4);

• designing the transfer matrix of the controller, H_C(s).

3 Robust Control Design Techniques

The general problem of robust design consists of finding a controller which assures the stability and robustness performances of the global system in the presence of disturbances or uncertainty.

Fig. 5.

The global robust control diagram.

The control diagram from Fig. 4 is modified in Fig. 5 to emphasize [9, 10, 13]:

• the augmented model of the system H_G(s) which may contain the nominal plant model and the disturbances;

• the controller matrix H_C(s);

• the input signal (which could include also the disturbances) u₁(s);

• the output signal y₁(s).

  

  (3)

The input-output relation from u₁ to the y₁ is described by the linear fractional transformation of the interconnected system:

$$ T_{y1u1} \left( s \right) = H_{11} \left( s \right) + H_{12} \left( s \right)H_{C} \left( s \right)\left[ {I - H_{22} \left( s \right)H_{C} \left( s \right)} \right]^{\, - 1} H_{21} \left( s \right). $$

(4)

3.1 H-infinity Technique

In the H-infinity technique the control law including H_C(s) is [10, 13]

$$ u_{2} \left( s \right) = H_{C} \left( s \right) \cdot y_{2} \left( s \right). $$

(5)

The global system with disturbances and uncertainty is stable and the H-infinity norm of the closed-loop system is bounded by a positive value $\gamma$.

$$ \left\| {T_{y1u1} } \right\|_{\infty } < \gamma $$

(6)

Using the terms of the augmented model (3) the ARE (algebraic Riccati equations) are:

$$ \begin{aligned} & A^{T} X + XA + X\left( {\gamma^{ - 2} B_{1} B_{1}^{T} - B_{2} B_{2}^{T} } \right)X + C_{1} C_{1}^{T} = 0 \\ & AY + YA^{T} + Y\left( {\gamma^{ - 2} C_{1}^{T} C_{1} - C_{2}^{T} C_{2} } \right)Y + B_{1}^{T} B_{1} = 0 \\ \end{aligned} $$

(7)

and the solutions X, Y are used then by the controller represented by (8).

(8)

The existing conditions of the optimal controller are:

• D₁₁ should be small enough so that: $D_{11} < \gamma$;

• the solutions X, Y of the ARE should be positive definite;

• $\lambda_{\max } \left( {XY} \right) < \gamma^{2}$ shows that eigenvalues are smaller than $\gamma^{2}$($\lambda_{\max }$- maximum value).

If all the weighting matrix are imposed than the general mixed sensitivity problem and the linear fractional transformation (4) becomes:

$$ T_{y1u1} \left( s \right) = \left[ {\begin{array}{*{20}c} {W_{e} \left( s \right)S\left( s \right)} \\ {W_{u} F\left( s \right)S\left( s \right)} \\ {W_{y} T\left( s \right)} \\ \end{array} } \right]. $$

(9)

The sensitivity function S(s) and the complementary sensitivity function T(s) are given in relation (10).

$$ \begin{aligned} & S\left( s \right) = E\left( s \right)R^{ - 1} \left( s \right) = \left[ {I - H_{C} \left( s \right)H_{P} \left( s \right)} \right]^{ - 1} \\ & T\left( s \right) = I - S\left( s \right) = H_{C} \left( s \right)H_{P} \left( s \right)\left[ {I - H_{C} \left( s \right)H_{P} \left( s \right)} \right]^{ - 1} \\ \end{aligned} $$

(10)

3.2 H2 Technique

In the H2 technique the matrix H_C(s) results from the optimization of the linear fractional transformation norm [10, 13]:

$$ \left\| {T_{y1u1} \left( s \right)} \right\|_{2} = \left\| {H_{11} \left( s \right) + H_{12} \left( s \right)H_{C} \left( s \right)\left[ {I - H_{22} \left( s \right)H_{C} \left( s \right)} \right]^{\, - 1} H_{21} \left( s \right)} \right\|_{2} < 1. $$

(11)

The symmetric matrix $V,\,N$ satisfies the existing conditions and the H2 controller is given by (12).

(12)

If $D_{21} \to 0$ then the H2 optimal control problem is similar to the LQG design.

4 Designing the MIMO Controller for the Two-Coupled Tanks

The robust control design is applied to the two-coupled tanks from Fig. 6 which is a MIMO system with two inputs and two outputs. According to [11] and [15]: LT₁, LT₂ are the level transducers; LC is the level control; FV₁, FV₂ are the flow valves, R₁, R₁₂, R₂ are the hydraulic resistances of the outlet and cross-coupling valves, F_a1, F_a2 are the inlet flows; F_e1, F_e12, F_e2 are the outlet flows; A₁, A₂ are the surfaces at the base of the tanks; L₁, L₂ are the levels of the fluid inside the tanks.

Fig. 6.

Two-coupled tanks MIMO plant.

The ISO (input-state-output) mathematical model which describes the dynamics of the system and time evolution of the levels of fluid in the tanks regarding the inlet and outlet flows of the fluid is deducted in (13) and (14) [11].

$$ \begin{aligned} & \left[ {\begin{array}{*{20}c} {\frac{d}{dt}L_{1} } \\ {\frac{d}{dt}L_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \frac{{R_{1} + R_{12} }}{{A_{1} R_{1} R_{12} }}} & {\frac{1}{{A_{1} R_{12} }}} \\ {\frac{1}{{A_{2} R_{12} }}} & { - \frac{{R_{2} + R_{12} }}{{A_{2} R_{2} R_{12} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {L_{1} } \\ {L_{2} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} {\frac{1}{{A_{1} }}} & 0 \\ 0 & {\frac{1}{{A_{2} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {F_{a1} } \\ {F_{a2} } \\ \end{array} } \right] \\ & \left[ {\begin{array}{*{20}c} {L_{1} } \\ {L_{2} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 \\ 0 & 1 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {L_{1} } \\ {L_{2} } \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 & 0 \\ 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {F_{a1} } \\ {F_{a2} } \\ \end{array} } \right] \\ \end{aligned} $$

(13)

$$ \left[ {\begin{array}{*{20}l} {L_{1} \left( s \right)} \hfill \\ {L_{2} \left( s \right)} \hfill \\ \end{array} } \right] = \left[ {\begin{array}{*{20}l} {H_{P11} \left( s \right)\;H_{P12} \left( s \right)} \hfill \\ {H_{P21} \left( s \right)\;H_{P22} \left( s \right)} \hfill \\ \end{array} } \right]\,\left[ {\begin{array}{*{20}l} {F_{a1} \left( s \right)} \hfill \\ {F_{a2} \left( s \right)} \hfill \\ \end{array} } \right] \equiv {\mathbf{Y}}\left( s \right) = {\mathbf{H}}_{P} \left( s \right) \cdot {\mathbf{U}}\left( s \right) $$

(14)

with H_P11(s), H_P22(s) the transfer functions on the direct channels of the MIMO system; H_P12(s), H_P21(s) the transfer functions on the cross-interaction channels.

In the case of MIMO systems is necessary to obtain the desired performances on each direct channel and compensate the cross-interaction effect, disturbances, and uncertainty. The solution for such issues is given by the robust control synthesis because its theory has the methodologies to design robust controllers.

The values $L_{1} = 0.4;\,L_{2} = 0.25;\,A_{1} = 0.028;\,A_{2} = 0.02$ are the main parameters used in simulations and $R_{1} = 0.8 \pm 25\%$; $R_{2} = 1.2 \pm 30\%$; $R_{12} = 1 \pm 20\%$ contain the additive uncertainty of the hydraulic resistances. So, the transfer matrix of the nominal plant given by (14) is:

$$ H_{P} \left( s \right) = \left[ {\begin{array}{*{20}c} {\frac{{35.71s + 3274}}{{\mathop {s^{2} + 172s + 5580}\limits_{{}} }}} & {\frac{{1786}}{{\mathop {s^{2} + 172s + 5580}\limits_{{}} }}} \\ {\frac{{1786}}{{s^{2} + 172s + 5580}}} & {\frac{{50s + 4018}}{{s^{2} + 172s + 5580}}} \\ \end{array} } \right]. $$

The step response behavior from Fig. 7 shows the effect of the uncertainty on each channel from the MIMO system and the weighting matrix for designing the robust controller is chosen according to [10, 12, 13].

Fig. 7.

The step response of the system with additive uncertainty (red is the nominal plant) [14].

$$ W_{e} \left( s \right) = \left[ {\begin{array}{*{20}c} {\frac{100}{{s + 0.5}}} & 0 \\ 0 & {\frac{100}{{s + 1}}} \\ \end{array} } \right];\quad W_{e} \left( s \right) = \left[ {\begin{array}{*{20}c} {10^{ - 3} } & 0 \\ 0 & {10^{ - 3} } \\ \end{array} } \right];\quad W_{y} \left( s \right) = \left[ {\begin{array}{*{20}c} \frac{3}{300} & 0 \\ 0 & \frac{s}{200} \\ \end{array} } \right]. $$

Before the determination of the transfer matrix (8) of the robust controller, the hinf Matlab function verifies the existing conditions (Fig. 8) [14].

$$ H_{C} (s) = \left[ {\begin{array}{*{20}l} {\frac{{1253s^{2} + 5.298e05s + 3.448e07}}{{\mathop {s^{3} + 677.2s^{2} + 1.148e05s + 5.724e04}\limits_{{}} }}} \hfill & {\frac{{ - 0.001296s^{2} - 4.475e04s - 1.532e07}}{{\mathop {s^{3} + 677.2s^{2} + 1.148e05s + 5.724e04}\limits_{{}} }}} \hfill \\ {\frac{{ - 0.007265s^{2} - 3.932e04s - 1.314e07}}{{s^{3} + 677.7s^{2} + 1.152e05s + 1.145e05}}} \hfill & {\frac{{786.3s^{2} + 3.349e05s + 2.409e07}}{{s^{3} + 677.7s^{2} + 1.152e05s + 1.145e05}}} \hfill \\ \end{array} } \right] $$

Fig. 8.

The check test for the H-infinity controller existing condition [14].

The response of the MIMO closed-loop system with uncertainty and including the H-infinity robust controller is presented in Fig. 9 [14].

In the H2 synthesis, the transfer matrix of the MIMO controller is given by (12) and is obtained with the h2lqg Matlab function.

$$ H_{C} \left( s \right) = \left[ {\begin{array}{*{20}c} {\frac{{836.5s^{2} + 2.337e05s + 1.338e07}}{{\mathop {s^{3} + 443.9s^{2} + 4.887e04s + 2.432e04}\limits_{{}} }}} & {\frac{{0.00063s^{2} - 2.988e04s - 5.946e06}}{{\mathop {s^{3} + 443.9s^{2} + 4.887e04s + 2.432e04}\limits_{{}} }}} \\ {\frac{{ - 0.00128s^{2} - 1.98e04s - 4.84e06}}{{s^{3} + 444.4s^{2} + 4.909e04s + 4.865e04}}} & {\frac{{396s^{2} + 1.331e05s + 8.874e06}}{{s^{3} + 444.4s^{2} + 4.909e04s + 4.865e04}}} \\ \end{array} } \right] $$

The response of the MIMO closed-loop system with uncertainty and including the H2 robust controller is presented in Fig. 10 [14]. Figure 11 shows a comparison of step input responses of the nominal closed-loop systems with both robust controllers, designed using the H2 and H-infinity synthesis.

Fig. 9.

The step input response of closed-loop MIMO system including the H-infinity robust controller (red is the nominal response) [14].

Fig. 10.

The step input response of the closed-loop MIMO system including the H2 robust controller (red is the nominal response) [14].

Fig. 11.

The step input responses of the closed-loop MIMO systems with both robust controllers, H2 controller (with blue) or H-infinity controller (with red) [14]

5 Conclusions

In a lot of applications, e.g. industrial control, the processes are cross-connected resulting in a MIMO configuration. Moreover, the systems are nonlinear and contain disturbances and uncertainty. These issues are not always solved by using conventional control.

In the simplest case, for negligible cross-coupling effect, the decoupling methodology consists of designing conventional controllers similar to SISO systems on the direct channel. If the cross-coupling effect is significant then other methods should be used to obtain the controller laws, e.g. desired behavior of the closed-loop system including or not the cross-interaction channels.

The presence of disturbances and uncertainty further complicates the design of the controller and then robust synthesis methods should be used (i.e. H2 and H-infinity synthesis). For MIMO systems, in the H-infinity design technique, the frequency domain performances are specified using the weighting matrix. So, the controllers are more complex and have higher-order structures, which means difficulties and higher costs for the practical implementation.

The paper presented some design aspects of H2 and H-infinity robust synthesis for MIMO systems. These methodologies are used for designing the two-coupled tanks control system. The process has two inputs and two outputs. In both scenarios, the closed-loop control performances meet the requirements regarding the overshoot, transient time, rising time, and steady-state error. These performances are emphasized in Fig. 9, Fig. 10, Fig. 11.

The control diagrams were tested including the uncertainty and the simulation results show stable responses of the closed-loop systems. The cross-influences (from F_a1 to L₂ and from F_a2 to L₁) are very small, thus being minimized. Robust Control Toolbox was used for designing the H2 and H-infinity robust controllers and finally, the closed-loop MIMO systems were simulated in the Matlab environment.

Further, in the study of the MIMO synthesis, some limitations of the control signals and possibilities to reduce the higher-order of the robust controllers will be considered, of course without affecting the overall performances of the dynamic regime.