Reduced Order Modeling for Thermo – Electric Processes

Abstract

In the study of any objects and devices, the first step is the construction of the geometric structure, which is divided into finite elements with large number of nodes. Such model with millions of degrees of freedom is inappropriate to use in control and data processing problems. Therefore, to solve this problem, a discrete model is constructed with a smaller number of degrees of freedom than in the original one. But with this approach to modeling related tasks, problems arise that need to be addressed. In this paper we will consider the ROM of electrothermal problems and effective methods for recording, isolating and storing elemental matrices obtained by CAD systems.

1 Introduction

Modeling of electro-thermal processes occupies one of the important parts in the developing of micro-electro-mechanical systems (MEMS) [1,2,3]. With a decrease in size and an increase in the complexity of MEMS it is no longer possible to neglect the mutual thermal effect between adjacent circuit elements [2]. Self-heating of each element in MEMS, for example, self-heating of transistors, will change not only the characteristics of the transistor itself, but also the whole system. The dominant effect – the Joule effect in MEMS will be a parasitic effect of heating and dissipation of heat (the transition of electrical energy to heat), as a result of which the characteristics of the MEMS will change and the system itself may become technologically unusable.

In order to study MEMS qualitatively, it is needful to go through a certain path in its construction. First, it is necessary to construct the geometry of this system, after which it must be divided into a sufficiently accurate finite element mesh. The order of the number of nodes can easily exceed 100000, but for the immersion of a given system into a system in state spaces, such a size of the system will be unsuitable for research. This is due to the fact that such a size of the problem will not provide time-optimal signal processing, tuning and verification of the system itself in the state space. Therefore, it is necessary to carry out the procedure for reducing the order of the settlement system, significantly reduced its order, but at the same time not losing anything in terms of the system reaction. So we will get a system suitable for research. This is what this work will be devoted to – we will analysis the thermoelectric processes and the construction of compact models.

2 Research of Thermoelectric Processes

Thermal conductivity is used to describe the thermal properties of any material. Thermal conductivity at the macroscopic level means that in the presence of a difference, a temperature gradient in a solid, thermal energy will move from a higher temperature region to a lower temperature region. This phenomenon is described by Fourier’s law:

$$ \vec{q} = - K\nabla T, $$

(1)

where $\vec{q}$ is the heat flux vector, $T$ is the temperature field, $K$ is the thermal conductivity coefficient.

The conductivity equation describes the flow of electric current in the presence of an electric potential gradient, if in Eq. (1) the temperature is replaced by the electric potential, and the vector of the heat flux is replaced by the vector of the electric current density $\vec{j}$, then the resulting equation is the equation of electrical conductivity:

$$ \vec{j} = - \sigma \nabla \varphi , $$

(2)

where $\sigma$ – electrical conductivity, $\varphi$ – electrical potential.

In the case of a coupled thermoelectric problem the expressions for the heat flux $\vec{q}$ and the electric current density vector $\vec{j}$ are modified according to the following effects:

The Peltier effect is the effect of energy transfer when an electric current passes at the point of contact between two dissimilar conductors.

The Thomson effect is a phenomenon, which consists in the fact that in a homogeneous unevenly heated conductor where an electric current flows, not only heat will be released due to the Joule-Lenz law, but also Thomson’s heat will be released or absorbed depending on the direction of the current flow.

Seebeck effect is the phenomenon of EMF at the ends of series-connected dissimilar conductors the contacts of which are at different temperatures. Thus, let us turn to a mathematical description of the problem of a coupled thermoelectric problem.

3 Mathematical Model

3.1 Problem Formulation

We write the coupled equations of heat conduction and the law of conservation of electric charge [1, 4] as

$$ \rho C\frac{\partial T}{{\partial t}} + \nabla \cdot \vec{q} = Q, $$

(3.a)

$$ \nabla \cdot \left( {\vec{j} + \frac{{\partial \vec{D}}}{\partial t}} \right) = 0, $$

(3.b)

which are related through the definition of the heat flux consisting of the heat flux described by the Fourier law and the flux caused by the Peltier effect.

$$ \vec{q} = \alpha T\vec{j} - K\nabla T, $$

(3.c)

$$ \vec{j} = \sigma \vec{E} - \sigma \alpha \nabla T. $$

(3.d)

The relationship between the vector of electrical permeability and vector of electric field intensity

$$ \vec{D} = \varepsilon \vec{E}, $$

(3.e)

where $\rho$ – density, $C$ – specific heat, $T$ – temperature, $Q$ – bulk density of heat generation, $\vec{q}$ – heat flow vector, $\vec{j}$ – current density vector, $\vec{E}$ – electric field vector, $\vec{D}$ – electric induction vector, $K$ – thermal conductivity, $\sigma$ – electrical conductivity, $\alpha$ – Seebeck coefficient, Π = Tα – Peltier coefficient, $\varepsilon$ – permittivity, $\nabla$ – del operator, $t$ – time.

3.2 Finite Element Formulation

Further, according to [1, 5], we write down the finite element supply of the coupled thermoelectric setting in order to understand which matrices and load vectors need to be found and uploaded to build a reduced model.

$$ \left[ {\begin{array}{*{20}c} {C^{TT} } & 0 \\ 0 & {C^{\varphi \varphi } } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{\dot{\mathbf{T}}}_{{\varvec{e}}} } \\ {{\dot{\mathbf{\varphi }}}_{{\varvec{e}}} } \\ \end{array} } \right\} + \left[ {\begin{array}{*{20}c} {K^{TT} } & 0 \\ {K^{\varphi T} } & {K^{\varphi \varphi } } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {{{\varvec{T}}}_{{\varvec{e}}} } \\ {{\varvec{\varphi }}_{{\varvec{e}}} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {Q + Q^P + Q^J } \\ I \\ \end{array} } \right\}, $$

(4)

where:

${{\varvec{N}}}$ – vector of element shapes functions,

${{\varvec{T}}}_{{\varvec{e}}}$ – vector of nodal temperatures,

${\varvec{\varphi }}_{{\varvec{e}}}$ – vector of nodal electric potentials,

$K^{TT} = \smallint \limits_V \nabla {{\varvec{N}}} \cdot \le \left[ K \right] \cdot \nabla {{\varvec{N}}}dV$ – thermal stiffness matrix,

$K^{\varphi \varphi } = \smallint \limits_V \nabla {{\varvec{N}}} \cdot \left[ \sigma \right] \cdot \nabla {{\varvec{N}}}dV$ – electric stiffness matrix,

$K^{\varphi T} = \smallint \limits_V \nabla {{\varvec{N}}} \cdot \left[ \sigma \right] \cdot \left[ \alpha \right] \cdot \nabla {{\varvec{N}}}dV$ – Seebeck stiffness matrix,

$C^{TT} = \rho \smallint \limits_V C{{\varvec{NN}}}dV$ – thermal damping matrix,

$C^{\varphi \varphi } = \smallint \limits_V \nabla {{\varvec{N}}} \cdot \left[ \varepsilon \right] \cdot \nabla {{\varvec{N}}}dV$ – dielectric damping matrix,

$Q^P = \smallint \limits_V \nabla {{\varvec{N}}} \cdot [\Pi ] \cdot {{\mathbf{J}}}dV$ – Peltier heat load vector,

$Q^J = \smallint \limits_V {{\varvec{NE}}} \cdot {{\mathbf{J}}}dV$ – electric power load vector,

$Q$ – vector of combined heat generation loads,

$I$ – electric current load.

4 Construct of Reduced Order Models of Thermoelectric System

At the first step of model reduction a geometric model of the object is constructed. After that we create a detailed finite element model with a large number of degrees of freedom, and in the end we formed a discrete model of the object with a least number of degrees of freedom than in the original finite element model using mathematical methods of reduction [2].

4.1 Finite Element Model

We create a computational domain for the problem under consideration. For such an area we will choose a rectangular area consisting of two different materials. The geometric model and finite element model of Peltier element are shown in Fig. 1. The construction and study of the finite element model will be carried out in the ANSYS APDL. The physical and geometric parameters of the system are shown in Table 1.

Fig. 1.

(a) Geometric model of the Peltier element, (b) finite element model of the Peltier element

Characteristics of the finite element model: number of nodes – 181, number of elements – 51, element type: plane77.

Table 1. Properties and dimensions of the Peltier element

According to Eq. (4) we consider only the governing equations for the heat equation. For further progress it is necessary to somehow determine and export from the ANSYS itself the vector of thermal loads Joule $Q^J$ and the Peltier load vector $Q^P$. To do this, consider two auxiliary problems.

At the first stage we consider a problem in which a Peltier heat flux vector $Q^P$ exists without boundary conditions and is specified at the junction of two materials. The boundary conditions in this case are shown in the Fig. 2.

Fig. 2.

Boundary conditions for determining the Peltier load vector

The peculiarity of this stage is that for the unambiguous determination of this vector, it is necessary to know the value of the nodal temperatures, which correspond to the junction of the two materials. This problem can be solved, for example, as follows – to carry out a direct calculation of the electrothermal problem [4] and extract from it the values of the corresponding nodal temperatures at the junction of two materials.

At the second stage, we will apply to the computational domain the heat sources responsible for heat generation due to Joule’s law. The boundary conditions in this case are shown in the Fig. 3.

Fig. 3.

Boundary conditions for determining the Joule load vector

Next we must pay attention to how we can perform calculations and unloading matrices in problems without boundary conditions. For this in the ANSYS APDL software package we will use the method of synthesizing the “component” forms (CMS – Component Mode Synthesis) [5]. This method is based on dividing a separate, complex and large model into a group of smaller problems [2]. Using this approach to the development and solution of almost any problem, the developer and researcher saves time and computing resources. Also, the motivation for using the CMS was the fact that it is possible to unload element matrices and load vectors in it without performing a complete calculation as such.

So, to upload the mass matrix M, the thermal conductivity matrix K and the Peltier heat load vector, we use the following ANSYS APDL built-in commands. It is also worth remembering that for each thermal effect, it is worth creating a separate calculation in order to avoid the imposition of load effects on each other in any nodes of the finite element model.

From the performed calculation, the matrices of mass, thermal conductivity and the Joule thermal load vector were written, which are saved in the files JouleMass.hb, JouleStiff.hb, and the load vector can be saved in any of these matrices [5]. Likewise for Peltier load vector. Next we will consider the very procedure of reduction and comparison of results in the Matlab software package.

4.2 Reduced Order Modeling in Matlab

Earlier we obtained the matrices of masses $M$ and thermal conductivity $K$, the Joule load vectors $Q^J$ and Peltier $Q^P$, which correspond to the considered finite element problems presented in Figs. 1, 2 and 3 without specifying boundary conditions, if they are available, then it is possible to write system (4) in the state space.

$$ \begin{array}{*{20}c} {E\dot{T} = AT + Bu, T_0 } \\ {y = CT} \\ \end{array} $$

(5)

The inclusion of boundary conditions in the problem shown in Figs. 1, 2 and 3 will change not only the matrices $M$ and $K$, but also the load vectors $Q^J$ and $Q^P$ themselves. Next, the question arises of how to take into account the presence of boundary conditions from the resulting system in the state space (5) without specifying them in the problems of Figs. 1, 2 and 3. For this, for example, consider the following approach. Suppose that zero temperature is set at the boundaries of the problem under consideration

$$ \left. T \right|_{x = 0} = \left. T \right|_{x = a} = 0 $$

(6.a)

Then the system (5) can be written in the form

$$ e_{11} \dot{T}_1 + e_{12} \dot{T}_2 + \ldots = a_{11} T_1 + a_{12} T_2 + \ldots + B_{11} u_1 + B_{12} u_2 + \ldots $$

(6.b)

We assume that the border corresponds to the nodes corresponding to the components $e_{11}$ and $e_{12}$. From a constant and zero value of the boundary conditions, it means that

$$ T_1 = 0,\dot{T}_1 = 0, T_2 = 0,\dot{T}_2 = 0 $$

(6.c)

This means excluding from consideration the nodes corresponding to the boundaries.

5 Results

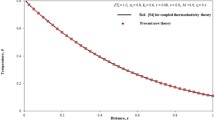
We will show the reaction of the initial system (5) taken from the ANSYS APDL and reduced by the 18th order model.

Fig. 4.

System responses to (a) stepwise action, (b) impulse action at zero initial and boundary conditions of the complete system (black line) and a reduced 18th order model (red dotted line)

Next we show Bode diagrams for the case of a complete system and a reduced system of the 18th order in Fig. 5.

Fig. 5.

Bode plots for the complete system (black line) and the reduced 18th order model (red dashed line)

From Figs. 4 and 5 it can be seen that the outputs of the complete system to typical influences fully meet our expectations, which indicates the correctness of the application of the CMS procedure. It was also found that the reduced 18th order model in its behavior completely coincides with the behavior of the complete system from ANSYS, which opens a further way in modeling control systems using already reduced models, which will significantly save calculation time.

6 Conclusion

Modeling of the thermoelectric processes in MEMS takes one of the important stages in their construction and operation. In finite element modeling the number of degrees of freedom can reach large values, even 10,000 nodes in this model is a problem in terms of compiling control systems for microsensors and microactuators, etc. It is necessary to use methods of model ordering order to reduce the computer time with the same exit from the object under study. Therefore, it is important to consider and verify the reduction techniques for electrothermal models.

In this paper, a method was considered for unloading the matrices of masses, stiffnesses and load vectors using superelement methods (CMS) in the Matlab software system. Then, using the built-in reduction methods, a reduced 18th order model was built. The outputs on typical actions and Bode diagrams of the complete and reduced models were compared and analyzed – they completely coincided. Thus, the reduced models open the way to the construction of the most convenient in terms of reducing the dimensionality of control objects for control systems, thereby saving calculation time and computing power of the computer.