Keywords

1 Introduction

As is known, the machining of workpieces requires relative motion between the workpiece and the tool and their force interaction. To transfer the shape-forming movements to workpieces or tools, it is necessary to fix them in a spindle assembly of the machine. Clamping mechanisms (CM) are used for this purpose. The characteristics of CM determine the possibility of using the maximum cutting speed and feed rate and consequently determine productivity and quality of the machining [1]. The magnitude of clamping forces determines the maximum value of the cutting forces that occur during machining. CM of the machines are located on the spindle and are part of the spindle assembly. Hence, requirements for CM are concerning possibilities of creating the required amount of clamping force for a minimum time, ensuring its stability in different modes of operation of the spindle assembly. Therefore, the design features of the CM have a significant impact on the characteristics of the whole spindle assembly as well. That determines the value of resonance (critical) frequency rotation, the possibility of accurate balancing [2] and keeping a balanced state during a given period of operation, etc.

2 Literature Review

There are several types of CM with mechanical and hydraulic converters of supplied energy. All the types have many disadvantages, including those caused by the presence of movable elements or working medium that can move in the radial direction under the action of centrifugal forces. It leads to a deterioration in the performance of the CM and the spindle assembly as a whole. Modern CM are subject to a number of requirements related to the possibility of their operation in the automatic machining cycle on CNC machines, the efficiency of control and regulation of the clamping force in real-time, reliability, energy efficiency, etc. To eliminate the above shortcomings, the design of the electromechanical clamping mechanism with collet chuck has been created (UA Patent No. 95323). The design does not contain elements that are movable in the radial direction. The use of an electric drive expands the possibilities for creating an effective control system of the new CM. Moreover, since it does not require creating special mechanical (hydraulic) subsystems in the machine for powering the new CM, it provides additional opportunities to design machines. It makes it especially easier to implement the new electromechanical CM into structures of new and existing machines.

The characteristics of CM determine the work characteristics of spindle assemblies and consequently productivity and quality of the machining. There are several studies related to the modeling of the processes of spindle assemblies as a whole without separation the dependencies that describe the operation characteristic of the clamping mechanism. There are studies concerning the operation of the clamping chuck [3]. The paper [4] targets a new design of a spindle system with an additional electromagnetic bearing. The paper [5] proposes modeling of spindle-holder assembly and investigates the contact characteristic under clamping and centrifugal forces. Thermal influence on spindle efficiency is considered in [6]. Influences of the axial depth of cut, the machining toolpath, and the initial clamping force on part distortion are shown in [7]. In [8], the method which allows knowing the clamping force from the torque applied by a dynamometric wrench is developed. In the research work [9], the method of cooling can be improved significantly by employing a model-based control strategy on a recirculation cooler unit. The paper [10] points out potential directions to consider when optimizing optimal sustainability performance. In [11], the research of characteristics of the electric motor operates as a part of the clamping mechanism with the corresponding type of load and the locking (stop-braking) mode of operation has been conducted. In the paper [12], a thermal compensation model is developed in a linear regression framework. A mathematical model of the genetic algorithm optimization design of the spindle is established in [13] according to the actual use of the spindle. The influence of the tool's characteristics [14] and the workpiece [15] on the quality of processing is also considered. In the study [16], variations of the mode shapes of the tool-spindle assembly at high spindle speeds are examined using numerical models, and hypotheses are formulated. Identification of interdependences of movement of the elements of the proposed CM is a prerequisite for optimizing its characteristics and consequently for improving the machining.

3 Research Methodology

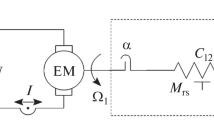
The operation of the CM is based on the work of an electric motor (see Fig. 1) whose stator is attached to the body of the machine, and the rotor is located on the threaded surface of the spindle. The rotor and spindle form a screw-type transmission, and during the rotor rotation, its axial movement is used to tighten the collet chuck for clamping the workpiece. The rotor (nut) rotation with an angular velocity ωд provides its axial motion with speed Vm transmitted to the tie-rod of the collet.

Fig. 1.
figure 1

Constructive scheme of CM (a) and scheme for the calculation of parameters (b).

Full size image

The clamping process can be conditionally divided into two stages according to the type of forces (dissipative or potential) acting in this CM at a certain stage of the clamping process:

  • backlash elimination in the CM – only active dissipative forces act;

  • creation of mechanical stress (tension) – the action of potential forces prevails due to significant deformation of an elastic system of the mechanism with insignificant forces of dissipative character.

The relationships among the kinematic parameters of the proposed CM design can be identified based on the equality between the ratio of the angle φд of the engine rotor rotation and the axial movement xm of the tie-rod connected to the collet.

$$ x_{m} = \frac{{\phi_{\partial } \cdot h}}{2\varPi} $$
(1)

where h – the pitch of the thread. After differentiation of Eq. (1) regarding time t, we obtain \(\frac{{\partial x_{m} }}{\partial t} = \frac{{\partial \phi_{\partial } }}{\partial t} \cdot \frac{h}{2\varPi}\) and

$$ V_{m} = \omega_{\partial } \cdot \frac{h}{2\varPi} = 0,5\omega_{\partial } \frac{h}{\varPi} = \omega_{\partial } \cdot 0,5d_{1} \cdot tg\psi $$
(2)

where \(d_{1}\) – the diameter of the thread, \(\Psi\) – the angle of rising of the thread. After representing \(0,5d_{1} \cdot tg\psi = i_{z}\) and putting into (2), we get \(V_{m} = \omega_{\partial } \cdot i_{z}\) or

$$ V_{m} = \mathop \phi \limits^{ \bullet }_{\partial } \cdot i_{z} . $$
(3)

The movement of the collet in the axial direction with speed Vm provides radial movement of its clamping segments with speed Vзe. The correlation between Vm and V3e can be found based on the equality between the ratios of the axial displacement xm of the tie-rod with collet and the radial displacement yзe of the clamping segments \(x_{m} = y_{3e} \cdot ctg\alpha\). From this dependence, it follows that

$$ y_{3e} = \frac{{x_{m} }}{ctg\alpha }, $$
(4)

\(\frac{{\partial x_{m} }}{\partial t} = \frac{{\partial y_{3e} }}{\partial t} \cdot ctg\alpha\), \(V_{m} = V_{3e} \cdot ctg\alpha\), \(\alpha\)- half the angle of a collet cone, \(ctg\alpha = i_{u}\) then

$$ V_{3e} = \frac{{V_{m} }}{{i_{u} }}. $$
(5)

After we put (3) in (5).

$$ V_{3e} = \frac{{\mathop {\phi_{\partial } }\limits^{ \bullet } \cdot i_{z} }}{{i_{u} }} = \mathop {\phi_{\partial } }\limits^{ \bullet } \frac{{i_{z} }}{{i_{u} }} $$
(6)

The frictional torque \(M_{z}^{T}\) in the screw transmission appears from the tangential component \(F_{t}\) of the friction forces with the arm \(0,5d_{1}\). The force \(F_{t}\) depends on the axial load \(S_{\sum }\) acting from the clamping chuck \(F_{t} = S_{\sum } \cdot tg\phi^{T}\), where \(\phi^{T}\) – the angle of friction in the threaded connection.

$$ M_{z}^{T} = 0,5 \cdot d_{1} \cdot S_{\sum } \cdot tg\phi^{T} $$
(7)

The friction force \(S_{u}^{T}\) in the conical coupling of the collet and the spindle with angle \(2\alpha\) is determined from the expression

$$ S_{u}^{T} = \frac{{z \cdot S_{\sum } }}{{\cos \alpha + {{\left( {\sin \alpha } \right)} \mathord{\left/ {\vphantom {{\left( {\sin \alpha } \right)} {f_{u} }}} \right. \kern-\nulldelimiterspace} {f_{u} }}}} $$
(8)

where z – the number of collet clamping segments; \(f_{u}\) – coefficient of friction in the conical coupling of the collet and the spindle.

The friction force \(S_{m}^{T}\) in the coupling of the tie-rod and the spindle is determined from the expression

$$ S_{m}^{T} = g \cdot m_{2} \cdot f_{m} $$
(9)

where \(g\) – free-fall acceleration; \(m_{2} = m_{m} + m_{n}\) – mass equal to the sum of the masses of the tie-rod and object of clamping; fm – coefficient of friction in the coupling of the tie-rod with the spindle.

The considered mechanism has one degree of freedom \(\phi_{\partial }\) – the angle of rotation of the rotor on which the position of the elements of the CM depends. The angle \(\phi_{\partial }\) is taken as a generalized coordinate relative to which the differential equation of motion of the system – the Lagrange's equations of the 2nd kind is composed

$$ \frac{d}{dt}\left( {\frac{\partial E}{{\partial \mathop {\phi_{\partial } }\limits^{ \bullet } }}} \right) - \frac{\partial E}{{\partial \phi_{\partial } }} = M_{\varPi} $$
(10)

E – is the kinetic energy of the mechanism; \(M_{\varPi}\) – generalized force, which in this case is equal to the main torque of external forces relative to the axis of the rotor rotation; t – time.

At both stages of working the CM, its kinetic energy E does not depend on the angle \(\phi_{\partial }\) of the rotor rotation, so the partial derivative of the kinetic energy E on the angle \(\phi_{\partial }\) is

$$ \frac{\partial E}{{\partial \phi_{\partial } }} = 0. $$
(11)

For the conditionally selected first stage of operation of the CM, when at the stage of backlash elimination there are only non-conservative (non-potential) forces, the Lagrange Eq. (10) considering (11) takes the form.

$$ \frac{d}{dt}\left( {\frac{\partial E}{{\partial \mathop {\phi_{\partial } }\limits^{ \bullet } }}} \right) = M_{\varPi} $$
(12)

The kinetic energy E of the CM is equal to the sum of the kinetic energies of its elements and is determined by the expression

$$ E = J_{\partial } \frac{{\phi_{\partial }^{ \bullet 2} }}{2} + m_{1} \frac{{V_{m}^{2} }}{2} + m_{3e} \frac{{V_{3e}^{2} }}{2} $$
(13)

where m1 = mp + mm + mu +mn, Jд – the moment of the rotor inertia relative to the axis of rotation; \(\phi_{\partial }\) – the rotation angle of the rotor; \(V_{m} ,V_{3e}\) – linear velocity of the tie-rod (and other elements with which it has the possibility of direct force interaction), the movement of the clamping segments in the radial direction; mp, mm, mu, mn – respectively, the mass of the rotor, tie-rod, collet and clamping object (assumed that the clamping object at the time of the clamping moves with the collet); \(m_{3e}\) – the mass of the clamping jaws, which move radially during clamping.

After (3) and (6) put in (13) \(E = J_{\partial } \frac{{\phi_{\partial }^{ \bullet 2} }}{2} + m_{1} \frac{{\phi_{\partial }^{ \bullet 2} }}{2}i_{z}^{2} + m_{3e} \frac{{\phi_{\partial }^{ \bullet 2} }}{2}\left( {\frac{{i_{z} }}{{i_{u} }}} \right)^{2}\)

$$ E = \frac{{\phi_{\partial }^{ \bullet \,2} }}{2}\left[ {J_{\partial } + m_{1} i_{z}^{2} + m_{3e} \left( {\frac{{i_{z} }}{{i_{u} }}} \right)^{2} } \right] = \frac{{\phi_{\partial }^{ \bullet \,2} }}{2}J_{\varPi} . $$
(14)

In Eq. (14), the value in square brackets is the moment of inertia \(J_{\varPi}\) of the CM reduced to the motor rotor.

$$ J_{\varPi} = \left[ {J_{\partial } + m_{1} i_{z}^{2} + m_{3e} \left( {\frac{{i_{z} }}{{i_{u} }}} \right)^{2} } \right] $$
(15)

Therefore (13) takes the form.

$$ E = \frac{{\phi_{\partial }^{ \bullet \,2} }}{2}J_{\varPi} $$
(16)

The partial derivative of the kinetic energy E (16) expression at the generalized velocity \(\mathop {\phi_{\partial } }\limits^{ \bullet }\) has the form \(\frac{\partial E}{{\partial \mathop {\phi_{\partial } }\limits^{ \bullet } }} = \mathop {\phi_{\partial } }\limits^{ \bullet } J_{\varPi}\). Since in the previous expression, when changing the time t changes only the angle \(\phi_{\partial }\), the time derivative of the partial derivative of the previous expression will be equal to

$$ \frac{d}{dt}\left( {\frac{\partial E}{{\partial \mathop {\phi_{\partial } }\limits^{ \bullet } }}} \right) = \mathop {\phi_{\partial } }\limits^{ \bullet \bullet } J_{\varPi} . $$
(17)

According to (17), expression (12) can be written in the following form.

$$ \mathop {\phi_{\partial } }\limits^{ \bullet \bullet } J_{\varPi } = M_{\varPi} $$
(18)

The generalized force \(M_{\varPi}\) (as the reduced moment) can be determined, taking into account the friction in the CM on the condition of equality of elementary works of forces acting in the mechanism as virtual works of active forces on small displacements

$$ M_{\varPi} \delta \phi_{\partial } = M_{\partial } \delta \phi_{\partial } - M_{z}^{T} \delta \phi_{\partial } - \delta x_{m} \left( {S_{m}^{T} + S_{u}^{T} + S_{nu} } \right) - T_{\sum } \frac{1}{3}\delta y_{3e} $$
(19)

where \(M_{z}^{T}\) and \(S_{m}^{T} ,\,\,S_{u}^{T}\), \(S_{nu}^{T}\) – the torque of friction forces in the screw transmission and the friction forces in the couplings respectively: the tie-rod with the spindle; the cone of the collet with the cone of the spindle; a clamping object with the feed collet; \(T_{\sum }\)– clamping force; \(\delta \phi_{\partial }\) and, \(\delta x_{m}\), \(\delta y_{3e}\) – the elementary angle of rotation in the direction of action \(M_{z}^{T}\) and movement in the direction of action, respectively \(S_{m}^{T}\),\(T_{\sum }\).

In dependencies (19), to simplify the calculations, the following assumptions are made. Due to the insignificant value of the angle \(\alpha\), the value of the relative displacement of the cone surfaces of the collet and the spindle is equal to the magnitude of the stroke of the tie-rod \(\delta x_{m}\). The part of the radial displacement of the clamping segment, which determines the effective work on the clamping of the workpiece (deformations in contacts of adjoining the surfaces of a clamping segment and an object of clamping) with force \(T_{\Sigma }\) is less than the total value of the radial displacement \(y_{3e}\) of the clamping segment during the clamping process. It depends on conditions of adjoining the surfaces of a clamping segment and an object of clamping. Therefore, in (19), the value of the radial displacement of the clamping segment during the action of force \(T_{\Sigma }\) and increasing mechanical tension in the coupling of a clamping segment and an object of clamping is conditionally assumed to be equal \(0.3y_{3e}\). Some possible exaggeration of the value of work from the action of the force \(T_{\Sigma }\), which resulting from this assumption, is partially offset in the overall balance of elementary works (8) by the presence of other elementary works (energy losses) that inevitably exist during the operation of the real CM.

4 Results

The relationship between the elementary angle \(\delta \phi_{\partial }\) of rotation of the rotor and the displacements \(\delta x_{m} = \delta \phi_{\partial } \frac{h}{2\varPi}\) is represented by analogy with (1) (4) \(\delta y_{3e} = \delta \phi_{\partial } \frac{h}{2\varPi} \cdot tg\alpha\). The forces included in (19) are presented in (7) (8) (9). The force of pushing the workpiece through the feed collet is determined from the expression \(S_{nu}^{{}} = P_{nu} (1 + K\Delta d)\), where \(P_{nu}\) – the pushing force of the workpiece with a diameter equal to the diameter of the hole in the feed collet; \(K = {A \mathord{\left/ {\vphantom {A {P_{nu} }}} \right. \kern-\nulldelimiterspace} {P_{nu} }}\) – coefficient of proportionality; A – change of force of pushing of a workpiece at the change of its diameter on each 0.2 -mm. After putting (7), (8), and (9) into (19), we get

$$ M_{\varPi} = M_{\partial } - 0,5d_{1} S_{\sum } tg\phi^{T} - \frac{h}{2\varPi}\left( {gm_{2} f_{m} + \frac{{zS_{\sum } }}{{\cos \alpha + {{\sin \alpha } \mathord{\left/ {\vphantom {{\sin \alpha } {f_{u} }}} \right. \kern-\nulldelimiterspace} {f_{u} }}}} + P_{nu} (1 + K\Delta d)} \right) - T_{\sum } \left( {\frac{1}{3}\frac{h}{2\varPi}tg\alpha } \right) $$
(20)

where \(S_{\sum } = \frac{{2M_{\partial }^{{}} }}{{d_{1} tg\psi }}\), \(\frac{h}{\varPi} = d_{1} tg\psi\).

Dependence (10) describes the system of non-conservative forces of the CM because of the absence of elastic forces at the stage of backlash elimination, and it makes it possible to make assumptions that before the appearance of tension, the dependence \(T_{\Sigma } = T_{\Sigma }^{0} = k \cdot y_{3e}\) is linear. There is a slight increase of \(T_{\Sigma }^{0}\) with magnification \(y_{3e}\) (small angle of the graph of the function), where \(k\) – a constant value that reflects the intensity of increasing the clamping force from the radial movement of a clamping segment and can be selected following the operating conditions of the CM.

$$ M_{\varPi} = M_{\partial } \left( {1 - \frac{{tg\phi^{T} }}{tg\psi } - \frac{z}{{\cos \alpha + {{\sin \alpha } \mathord{\left/ {\vphantom {{\sin \alpha } f}} \right. \kern-\nulldelimiterspace} f}_{u} }}} \right) - \frac{h}{2\varPi}\left( {gm_{2} f_{m} + P_{nu} (1 + K\Delta d)} \right) - T_{\Sigma }^{0} \frac{h}{6\varPi}tg\alpha $$
(21)

Considering (4) \(T_{\Sigma }^{0} = \phi_{\partial } \frac{k \cdot h}{{2\varPi}}tg\alpha\) and \(\frac{h}{\varPi} = d_{1} tg\psi\) are put into (21) and two first summands that do not contain variables are denoted by symbols \(\beta_{1}\).

$$ \theta_{1} = M_{\partial } \left( {1 - \frac{{tg\phi^{T} }}{tg\psi } - \frac{z}{{\cos \alpha + {{\sin \alpha } \mathord{\left/ {\vphantom {{\sin \alpha } {f_{u} }}} \right. \kern-\nulldelimiterspace} {f_{u} }}}}} \right) - \frac{h}{2\varPi}\left( {gm_{2} f_{m} + P_{nu} (1 + K\Delta d)} \right) $$
(22)
$$ \beta_{1} = - \frac{{k \cdot h^{2} }}{{12\pi^{2} }}tg^{2} \alpha = - \frac{k}{12}d_{1}^{2} tg^{2} \psi \cdot tg^{2} \alpha $$
(23)
$$ M_{\varPi} = \theta_{1} + \beta_{1} \phi_{\partial } $$
(24)

Substituting (24) for (18), we obtain a differential equation of the following form.

$$ \mathop {\phi_{\partial } }\limits^{ \bullet \bullet } J_{\varPi} = \theta_{1} + \beta_{1} \phi_{\partial } $$
(25)

Reassignment in (25) \(\theta = \frac{{\theta_{1} }}{{J_{\varPi} }}\) and \(\beta = \frac{{\beta_{1} }}{{J_{\varPi} }}\).

$$ \mathop {\phi_{\partial } }\limits^{ \bullet \bullet } = \theta + \beta \phi_{\partial } $$
(26)

When \(\frac{{d\phi_{\partial } }}{dt} = \omega\) then \(\frac{{d^{2} \phi_{\partial } }}{{dt^{2} }} = \frac{d\omega }{{dt}} = \frac{d\omega }{{d\phi_{\partial } }} \cdot \frac{{d\phi_{\partial } }}{dt} = \frac{d\omega }{{d\phi_{\partial } }}\omega\) and consequently \(\frac{d\omega }{{d\phi_{\partial } }}\omega = \theta + \beta \phi_{\partial }\); \(\int {\omega d\omega = \int {\left( {\theta + \beta \phi_{\partial } } \right)d\phi_{\partial } } }\); \(\frac{{\omega^{2} }}{2} = \theta \phi_{\partial } + \beta \frac{{\phi_{\partial }^{2} }}{2}\, + C_{1}\). The constant of integration C1 is defined from initial conditions. At the initial moment of time, the speed of the rotor relative to the spindle is equal to zero (but the rotor relative to the stator can rotate with the velocity of the spindle) \(\phi_{\partial } = 0\) \(\omega = 0\), \(C_{1} = 0\) consequently \(\frac{{d\phi_{\partial } }}{dt} = \sqrt {\beta \phi_{\partial }^{2} + 2\theta \phi_{\partial } }\) or \(\int {\frac{{d\phi_{\partial } }}{{\sqrt {\beta \phi_{\partial }^{2} + 2\theta \phi_{\partial } } }}} = \int {dt + C_{2}^{/} }\) and \(\int {\frac{{d\phi_{\partial } }}{{\sqrt {\beta \phi_{\partial }^{2} + 2\theta \phi_{\partial } } }}} = \frac{1}{\sqrt \beta }\ln \left[ {2\beta \phi_{\partial } + 2\theta + 2\sqrt {2\theta \beta \phi_{\partial } + \beta^{2} \phi_{\partial }^{2} } } \right]\). The solution of the previous equation can be written as follows \(\ln \left[ {2\beta \phi_{\partial } + 2\theta + 2\sqrt {2\theta \beta \phi_{\partial } + \beta^{2} \phi_{\partial }^{2} } } \right] = \sqrt \beta \cdot t + C_{2}\). The constant C2 can be found from the initial condition when \(t = 0\), \(\phi_{\partial } = 0\). Consequently \(\ln 2\theta = C_{2}\). Substitute in the previous expression \(\frac{\beta }{\theta }\phi_{\partial } + \sqrt {2\frac{\beta }{\theta }\phi_{\partial } + \frac{{\beta^{2} }}{{\theta^{2} }}\phi_{\partial }^{2} } = e^{\sqrt \beta \cdot t} - 1\).

$$ \phi_{\partial }^{{}} = \frac{{\left( {e^{\sqrt \beta \cdot t} - 1} \right)^{2} }}{{2\frac{\beta }{\theta }e^{\sqrt \beta \cdot t} }} $$
(27)

The value \(\beta\) is characteristic because its positive values determine the monotonic increase of the function (27) and in the case of negative values – local declines and rises (fluctuations) are possible. Equation (27) describes the dependence of the generalized coordinate \(\phi_{\partial }\) on time at the stage of elimination of backlashes (under the action of non-conservative forces) in the CM, which makes it possible to determine motion characteristics of the CM elements through dependences describing their position depending on \(\phi_{\partial }\).

5 Conclusions

The presented researches are a part of researches on a new patented design of the clamping mechanism. The received mathematical dependencies reflect the influence on the operation of the mechanism of forces of friction, mass, and geometrical characteristics of its elements at the stage of backlash elimination. Obtained formula (27) describes the dependence of the generalized coordinate \(\phi_{\partial }\)on-time t and shows, for example, that the decrease in mass \(m_{2}\), friction force fm, and angle \(\alpha\) causes an increase in value \(\theta_{1}\) and, as a result, increase values \(\theta\) and \(\phi_{\partial }\). It means increasing the movement speed of the elements and reducing the time on the backlash elimination process. The mathematical model can be used to calculate parameters of the mechanism's elements to provide performance characteristics and is a prerequisite for the possibility of design optimizing.