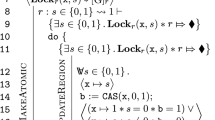1 Introduction

Standard separation logic enables the modular verification of heap-manipulating sequential [25, 33] and data-race free concurrent programs [4, 24]. More recently, numerous separation logics have been proposed that enable the verification of fine-grained concurrency by incorporating ideas from concurrent separation logic, Owicki-Gries [28], and rely-guarantee [15]. Examples include CAP [7], iCAP [40], CaReSL [42], CoLoSL [32], FCSL [37], GPS [43], RSL [45], and TaDA [35] (see Brookes et al. [3] for an overview). These logics are very expressive, but challenging to apply because they often comprise many complex proof rules. E.g. our running example (Fig. 1) consists of two statements, but requires over 20 rule applications in TaDA, many of which have non-trivial instantiations and subtle side conditions. This complexity seems inevitable for challenging verification problems involving, e.g. fine-grained concurrency or weak memory.

The complexity of advanced separation logics makes it difficult to develop proofs in these logics. It is, thus, crucial to have tools that check the validity of proofs and automate parts of the proof search. One way to provide this tool support is through proof checkers, which take as input a nearly complete proof and check its validity. They typically embed program logics into the higher-order logic of an interactive theorem prover such as Coq. Proof checkers exist, e.g. for RSL [45] and FCSL [37]. Alternatively, automated verifiers take as input a program with specifications and devise the proof automatically. They typically combine existing reasoning engines such as SMT solvers with logic-specific proof search algorithms. Examples are Smallfoot [2] and Grasshopper [31] for traditional separation logics, and Caper [8] for fine-grained concurrency.

Proof checkers and automated verifiers strike different trade-offs in the design space. Proof checkers are typically very expressive, enabling the verification of complex programs and properties, and produce foundational proofs. However, existing proof checkers offer little automation. Automated verifiers, on the other hand, significantly reduce the proof effort, but compromise on expressiveness and require substantial development effort, especially, to devise custom proof search algorithms.

It is in principle possible to increase the automation of proof checkers by developing proof tactics, or to increase the expressiveness of automated verifiers by developing stronger custom proof search algorithms. However, such developments are too costly for the vast majority of program logics, which serve mostly a scientific or educational purpose. As a result, adequate tool support is very rare, which makes it difficult for developers of such logics, lecturers and students, as well as engineers to apply, and gain experience with, such logics.

To remedy the situation, several tools took inspiration from the idea of proof outlines [1, 27], formal proof skeletons that contain the key proof steps, but omit most of the details. Proof outlines are a standard notation to present program proofs in publications and teaching material. Proof outline checkers such as Starling [46] and VeriFast [14] take as input a proof outline and then check automatically that it represents a valid proof in the program logic. They provide automation for proof steps for which good proof search algorithms exist, and can support expressive logics by requiring annotations for complex proof steps. Due to this flexibility, proof outline checkers are especially useful for experimenting with a logic, in situations where foundational proofs are not essential.

In this paper, we present Voila, a proof outline checker for TaDA [35], which goes beyond existing proof outline checkers and automated verifiers by supporting a substantially more complex program logic, handling fine-grained concurrency, linearizability, abstract atomicity, and other advanced features. We believe that our systematic development of Voila generalizes to other complex logics. Our contributions are as follows:

  • The Voila proof outline language, which supports a large subset of TaDA and enables users to write proof outlines very similar to those used by the TaDA authors [34, 35] (Sect. 3).

  • A systematic approach to automate the expansion of a proof outline into a full proof candidate via a normal form and heuristics (Sect. 5). Our approach automates most proof steps (20 out of 22 in the running example from Fig. 1).

  • An encoding of the proof candidate into Viper [22], which checks its validity without requiring any TaDA-specific proof search algorithms (Sect. 6).

  • The Voila proof outline checker, the first tool that supports specification for linearization points, provides a high degree of automation, and achieves good performance (Sect. 7). Our submission artifact with the Voila tool ready-to-use can be found at [49], and the Voila source repository is located at [48].

Outline. Section 2 gives an overview of the TaDA logic and illustrates our approach. Section 3 presents the Voila proof outline language, and Sect. 4 summarizes how we verify proof outlines. We explain how we automatically expand a proof outline into a proof candidate in Sect. 5 and how we encode a proof candidate into Viper in Sect. 6. In Sect. 7, we evaluate our technique by verifying several challenging examples, discuss related work in Sect. 8, and conclude in Sect. 9.

The full version of our paper [47] contains a substantial appendix with many further details, including: the full version and Viper encoding of our running example, with TaDA levels (omitted from this paper, but supported by Voila) and nested regions; additional inference heuristics; general Viper encoding scheme; encoding of a custom guard algebra; and a substantial soundness sketch.

2 Running Example and TaDA Overview

Figure 1 shows our running example: a TaDA proof outline for the procedure of a spinlock. As in the original publication [35], the outline shows only two out of 22 proof steps and omits most side conditions. We use this example to introduce the necessary TaDA background, explain TaDA proof outlines, and illustrate the corresponding Voila proof outline.

Fig. 1.
figure 1

TaDA spinlock example with shared region ; adapted with only minor changes from TaDA [35]. The lock region (lines 1–2) comprises a single memory location, whose value is either 0 (available) or 1 (acquired). Guard G allows locking and unlocking (lines 3–4), and is unique (line 5). The proof outline (lines 6–22) shows a CAS-based operation with atomic specifications. An enclosing region ( in da Rocha Pinto et al. [35], verifiable by Voila and shown in the full paper [47] then establishes the usual lock semantics. Levels (denoted by \(\lambda \) in TaDA) are omitted from the discussion in this paper, but supported by Voila and included in the full paper [47].

Full size image

2.1 Regions and Atomicity

TaDA targets shared-memory concurrency with sequentially consistent memory. TaDA programs manipulate shared regions, data structures that are concurrently modified according to a specified protocol (as in rely-guarantee reasoning [15]). A shared region such as is an abstraction over the region’s content, analogous to abstract predicates [30] in traditional separation logic. In our example (lines 1–2), the lock owns memory location x (denoted by separation logic’s points-to predicate \(x \mapsto \_\)), and its abstract state s is 0 or 1, indicating whether it is unlocked or locked. Here, the abstract state and the content of the memory location coincide, but they may differ in general. The subscript r uniquely identifies a region instance. Note that TaDA’s region assertions are duplicable, such that multiple threads may obtain an instance of the resource and invoke operations on the lock.

Lines 3–5 define the protocol for modifications of a lock as a labeled transition system. The labels are guards – abstract resources that restrict when a transition may be taken. Here, guard G allows both locking and unlocking (lines 3–4), and is unique (line 5). Most lock specifications use duplicable guards to allow multiple threads to compete for the lock; in this example, the usual lock semantics is established by an enclosing region (  [35]; see the full paper [47]).

Lines 6–22 contain the proof outline for the procedure, which updates a lock from an undetermined state – it can seesaw between locked and unlocked due to environment interference – to the locked state. Importantly, this update appears to be atomic to clients of the spinlock. These properties are expressed by the atomic TaDA triple (lines 6, 7, and 22)

figure j

Atomic triples (angle brackets) express that their statement is linearizable [13]. The abstract state of shared regions occurring in pre- and postconditions of atomic triples is interpreted relative to the linearization point, i.e. the moment in time when the update becomes visible to other threads (here, when the CAS operation on line 14 succeeds). The interference context is a special binding for the abstract region state that forces callers to guarantee that the environment keeps the lock state in \(\{0,1\}\) until the linearization point is reached (a vacuous restriction in this case).

The precondition of the triple states that an instance of guard G for region r, , is required to execute . The postcondition expresses that, at the linearization point, the lock’s abstract state was changed from unlocked (\(s = 0\)) to locked ( ). In general, callers must assume that a region’s abstract state may have been changed by the environment after the linearization point was reached; here, however, the presence of the unique guard enables the caller of to conclude (by the transition system) that the lock remains locked.

Fig. 2.
figure 2

Simplified versions of two key TaDA rules used in Fig. 1. MakeAtomic establishes an atomic triple (conclusion) for a linearizable block of code (premise), which includes checking that a state update complies with the region’s transition system: \(\mathcal {T}_\textit{R}(G)^{*}\) is the reflexive, transitive closure of the transitions that G allows. UpdateRegion identifies a linearization point, for instance, a CAS statement. If successful, the diamond tracking resource is exchanged for the witness tracking resource to record the performed state update; otherwise, the diamond resource is kept, such that the operation can be attempted again.

Full size image

2.2 TaDA Proof Outline

Lines 6–22 of the proof outline in Fig. 1 show the main proof steps; Fig. 2 shows simplified versions of the applied key TaDA rules. MakeAtomic establishes an atomic triple by checking that a block of code is atomic w.r.t. a shared region abstraction (hence the change from non-atomic premise triple, written with curly braces, to an atomic conclusion triple). UpdateRegion identifies the linearization point inside this code block. Rule MakeAtomic requires that the atomicity context, a set \(\mathcal {A}\) of pending updates, of the premise triple includes any region updates performed by the statement of the triple (there can be at most one such update per region). In the proof outline, this requirement is reflected on line 8, which shows the intended update of the lock’s state: (following TaDA publications, we omitted the tail of the atomicity context from the outline). MakeAtomic checks that the update is allowed by the region’s transition system with the available guards (the rule’s second premise in Fig. 2), but the check is omitted from the proof outline. Then MakeAtomic temporarily exchanges the corresponding guard for the diamond tracking resource (line 9), which serves as evidence that the intended update was not yet performed.

Inside the loop, an application of UpdateRegion identifies the CAS (line 14) as the linearization point. The rule requires the diamond resource in its precondition (line 11), modifies the shared region (lines 12–16), and case-splits in its postcondition: if the update failed (line 19) then the diamond is kept for the next attempt; otherwise (line 18), the diamond is exchanged for the witness tracking resource , which indicates that the region was updated from abstract state 0 to 1. At the end of MakeAtomic (lines 21–22), the witness resource is consumed and the desired abstractly atomic postcondition is established, stating that the shared region was updated from 0 to 1 at the linearization point.

2.3 Voila Proof Outline

Figure 3 shows the complete proof outline of our example in the Voila proof outline language, which closely resembles the TaDA outline from Fig. 1. In particular, the declaration defines a region’s interpretation, abstract state, and transition system, just like the initial declarations in Fig. 1. The subsequent proof outline for procedure annotates the same two rule applications as the TaDA outline and a very similar loop invariant. The Voila proof outline verifies automatically via an encoding into Viper, but the outline is expressed completely in terms of TaDA concepts; it does not expose any details of the underlying verification infrastructure. This means that our tool automatically infers the additional 20 rule applications, and all omitted side conditions, thereby closing the gap between the user-provided proof outline and a corresponding full-fledged proof.

Fig. 3.
figure 3

The Voila proof outline of our example, strongly resembling the TaDA proof outline from Fig. 1. is the type of region identifiers; primitive types are passed by value, structs by reference. Logical variables are introduced using a question mark; e.g.   binds the logical variable to the value of the location . denotes separating conjunction.

Full size image

3 Proof Outline Language

Proof outlines annotate programs with rule applications of a given program logic. These annotations indicate where to apply rules and how to instantiate their meta-variables. The goal of a proof outline is to convey the essential proof steps; ideally, consumers of such outlines can then construct a full proof with modest effort. Consumers may be human readers [27], or tools that automatically check the validity of a proof outline [14, 21, 46]; our focus is on the latter.

The key challenge of designing a proof outline language is to define annotations that accomplish this goal with low annotation overhead for proof outline authors. To approach this challenge systematically, we classify the rules of the program logic (here: TaDA) into three categories: (1) For some rules, the program prescribes where and how to apply them, i.e. they do not require any annotations. We call such rules syntax-driven rules. An example in standard Hoare logic is the assignment rule, where the assignment statement prescribes how to manipulate the adjacent assertions. (2) Some rules can be applied and instantiated in many meaningful ways. For such rules, the author of the proof outline needs to indicate where or how to apply them through suitable annotations. Since such rules often indicate essential proof steps, we call them key rules. In proof outlines for standard Hoare logic, the while-rule typically requires an annotation how to apply it, namely the loop invariant. The rule of consequence typically requires an annotation where and how to apply it, e.g. to strengthen the precondition of a triple or to weaken its postcondition. (3) The effort of authoring a proof outline can be greatly reduced by applying some rules heuristically, based on information already present in the outline. We call such rules bridge rules. Heuristics reduce the annotation overhead, but may lead to incompleteness if they fail; a proof outline language may provide annotations to complement the heuristics in such situations, slightly blurring the distinction between key and bridge rules. E.g. the Dafny verifier [20] applies heuristics to guess termination measures for loops, but also offers an annotation to provide a measure manually, if necessary.

The rule classification depends on the proof search capabilities of the verification tool that is used to check the proof outline. We use Viper [22], which provides a high degree of automation for standard separation logic and, thus, allows us to focus on the specific aspects of TaDA.

In the rest of this section, we give an overview of the Voila proof outline language and, in particular, discuss which TaDA rules are supported as syntax-driven, key, and bridge rules. Voila’s grammar can be found in the full paper [47], showing that Voila strongly resembles TaDA, but requires fewer technical details.

Expressions and Statements. Voila supports all of TaDA’s programming language constructs, including variables and heap locations, primitive types and operations thereon, atomic heap reads and writes, loops, and procedure calls. Consequently, Voila supports the corresponding syntax-driven TaDA rules.

Background Definitions. Voila’s syntax for declaring regions and transitions closely resembles TaDA, but e.g. subscripts are replaced by additional parameters, such as the region identifier . A region declaration defines the region’s content via an assertion, and its value via a function. The latter may refer to region parameters, as well as values bound in the interpretation, such as in the example from Fig. 3. The region’s transition system is declared by introducing the guards and the permitted actions, i.e. transitions. Voila includes several built-in guard algebras (adopted from Caper [8]); additional ones can be encoded, see the full paper [47]. A region declaration introduces a corresponding region predicate, which has an additional out-parameter that yields the region’s abstract state (e.g.   in the precondition of procedure in Fig. 3), as defined by the function. We omit this out-parameter when its value is irrelevant.

Specifications. Voila proof outlines require specifications for procedures, and invariants for loops; we again chose a TaDA-like syntax for familiarity. Explicit loop invariants are required by Viper, but also enable us to automatically instantiate certain bridge rules (see framing in Sect. 5).

Recall that specifications in TaDA are written as atomic or non-atomic triples, and include an interference context and an atomicity context. Voila simplifies the notation significantly by requiring these contexts only for abstractly-atomic procedure specifications; for all statements and rule applications, they are determined automatically, despite changing regularly during a proof. For procedures with abstractly-atomic behavior (modifier ), the interference context is declared through the clause. E.g. for procedure from Fig. 3, it corresponds to TaDA’s interference context .

Key Rules. In addition to procedure and loop specifications, Voila requires user input only for the following fundamental TaDA rules: UpdateRegion, MakeAtomic, UseAtomic, and OpenRegion; applications of all other rules are automated. Since they capture the core ideas behind TaDA, these rules are among the most complex rules of the logic and admit a vast proof search space. Therefore, their annotation is essential, for both human readers [34, 35] and automatic checkers. As seen in Fig. 3, the annotations for these key rules include only the used region and, for updates, the used guard; all other information present in the corresponding TaDA rules is derived automatically.

Bridge Rules. All other TaDA rules are applied automatically, and thus have no Voila counterparts. This includes all structural rules for manipulating triple atomicity (e.g. AWeakening1, AExists), interference contexts (e.g. Substitution, AWeakening2), and levels (e.g. AWeakening3). Their applications are heuristically derived from the program, applications of key rules, and adjacent triples. TaDA’s frame rule is also automatically applied by leveraging Viper’s built-in support for framing, combined with additional encoding steps to satisfy TaDA’s frame stability side condition. Finally, TaDA entailments are bridge rules when they can be automated by the used verification tool. For Viper, this is the case for standard separation logic entailments, which constitute the majority of entailments to perform. To support TaDA’s view shifts [6, 34] – entailments similar to the classical rule of consequence, but involving arbitrary definitions of regions and guard algebras – Voila provides specialized annotations.

4 Proof Workflow

Our approach, and corresponding implementation, enables the following workflow: users provide a proof outline and possibly some annotations for complex entailments, but never need to insert any other rule. Hence, if the outline summarizes a valid proof, verification is automatic, without a tedious process of manually applying additional rules. If the outline is invalid, our tool reports which specification (e.g. loop invariant) it could not prove or which key rule application it could not verify, and why (e.g. missing guard).

Achieving this workflow, however, is challenging: by design, proof outlines provide the important proof steps, but are not complete proofs. Consider, e.g. the TaDA and Voila outlines from Fig. 1 and Fig. 3, respectively. Applying UpdateRegion produces an atomic triple in its conclusion, whereas the while-rule requires a non-atomic triple for the loop body. A complete proof needs to perform the necessary adjustment through additional applications of bridge rules, which are not present in the proof outlines, and thus need to be inferred.

Our workflow is enabled by first expanding proof outlines into proof candidates, in two main steps: step 1 automatically inserts the applications of all syntax-driven rules; step 2 expands further by applying heuristics to insert bridge rule applications. The resulting proof candidate contains the applications of all rules of the program logic. Afterwards, we check that the proof candidate corresponds to a valid proof, by encoding it as a Viper program that checks whether all proof rules are applied correctly. Our actual implementation deviates slightly from this conceptual structure, e.g. because Viper does not require one to make the application of syntax-driven rules, framing, and entailment checking explicit.

5 Expanding Proof Outlines to Proof Candidates

Automatically expanding a proof outline is ultimately a proof search problem, with a vast search space in case of complex logics such as TaDA. Our choice of key rules (and corresponding annotations) reduces the search space, but it remains vast, due to TaDA’s many structural rules that can be applied to almost all triples. To further reduce the search space, without introducing additional annotation overhead, we devised (and enforce) a normal form for proof candidate triples. Our normal form allows us to define heuristics for the application of bridge rules locally, based only on adjacent rule applications, without having to inspect larger proof parts. This locality reduces the search space substantially, and enables us to automatically close the gap between user-provided proof outline and finally verified proof candidate. In our running example, our heuristics infer 20 out of 22 rule applications.

It might be helpful to consider an analogy with standard Hoare logic: its rule of consequence can be applied to each Hoare triple. A suitable normal form could restrict proofs to use the rule of consequence only at the beginning of the program and for each loop (as in a weakest-precondition calculus). A heuristic can then infer the concrete applications, in particular, the entailments used in the rule application, treating the rule as a bridge rule.

Normal Form. Our normal is established by a combination of syntactic checks and proof obligations in the final Viper encoding. Its main restrictions are as follows: (1) All triples are either exclusively atomic or non-atomic, which enables us to infer the triple kinds from statements and key rule applications. Due to this restriction, Voila cannot express specifications that combine atomic and non-atomic behaviors. However, such specifications do not occur frequently (see Sect. 5.2.3 in [34] for an example) and could be supported via additional annotations. (2) All triple preconditions, as well as the postconditions of non-atomic triples, are stable, i.e. cannot be invalidated by (legal) concurrent operations. In contrast, TaDA requires stability only for certain assertions. Our stronger requirement enables us to rely on stability at various points in the proof instead of having to check it – most importantly, when Viper automatically applies its frame rule. To enforce this restriction, we eagerly stabilize assertions through suitable weakening steps. (3) In atomic triples, the state of every region is bound by exactly one interference quantifier ( ), which simplifies the manipulation of interference contexts, e.g. for procedure calls. To the best of our knowledge, this restriction does not limit the expressiveness of Voila proofs. (4) Triples must hold for a range of atomicity contexts \(\mathcal {A}\), rather than just a single context. This stronger proof obligation rules out certain applications of MakeAtomic – which we have seen only in contrived examples – but it increases automation substantially and improves procedure modularity.

By design, our normal form prevents Voila from constructing certain TaDA proofs. However, the only practical limitation is that Voila does not support TaDA’s combination of atomic and non-atomic behavior in a single triple. As far as we are aware, all other normal form restrictions do not limit expressiveness for practical examples, or can be worked around in systematic ways.

Heuristics. We employ five main heuristics: to determine when to change triple atomicity, to ensure stable frames by construction, to compute atomicity context ranges, to compute levels, and to compute interference contexts in procedure body proofs. All heuristics are based on inspecting adjacent rule applications and their proof state. We briefly discuss the first three heuristics here, and refer readers to the full paper [47] for the remaining two heuristics. There, we give a more detailed explanation, and illustrate our heuristics in the context of our running example. (1) Changing triple atomicity corresponds to an application of (at least) TaDA rule AWeakening1, necessary when a non-atomic composite statement (e.g. the statement in Fig. 1) has an abstract-atomic sub-statement (e.g. the atomic CAS in Fig. 1). We infer all applications of this rule. (2) A more complex heuristic is used in the context of framing: TaDA’s frame rule requires the frame, i.e., the assertion preserved across a statement, to be stable. For simple statements such as heap accesses, it is sound to rely on Viper’s built-in support for framing. For composite statements with arbitrary user-provided footprints (assertions such as a loop invariant describing which resources the composite statement may modify), we greedily infer frame rule applications that attempt to preserve all information outside the footprint. The inferred applications are later encoded in Viper such that the resulting frame is stable, by applying suitable weakening steps. (3) Atomicity context ranges are heuristically inferred from currently owned tracking resources and level information. Atomicity contexts are not manipulated by a specific TaDA rule, but they need to be instantiated when applying rules: most importantly, TaDA’s procedure call rule, but also e.g. MakeAtomic and UpdateRegion (see Fig. 2).

In our experience, our heuristics fail only in two scenarios: the first are contrived examples, concerned with TaDA resources in isolation, not properties of actual code – where they fail to expand a proof outline into a valid proof. More relevant is the second scenario, where our heuristics yield a valid proof that Viper then fails to verify because it requires entailments that Viper cannot discharge automatically. To work around such problems when they occur, Voila allows programmers to provide additional annotations to indicate where to apply complex entailments.

Importantly, a failure of our heuristics does not compromise soundness: if they infer invalid bridge rule applications, e.g. whose side conditions do not hold, the resulting invalid proof candidates are rejected by Viper in the final validation.

6 Validating Proof Candidates in Viper

Proof candidates – i.e. the user-provided program with heuristically inserted bridge rule applications – do not necessarily represent valid proofs, e.g. when users provide incorrect loop invariants. To check whether a proof candidate actually represents a valid proof, we need to verify (1) that each rule is applied correctly, in particular, that its premises and side conditions hold, and (2) that the property shown by the proof candidate entails the intended specification. To validate proof candidates automatically, we use the existing Viper tool [22]. In this section, we give a high-level overview of how we encode proof candidates into the Viper language.

Viper Language. Viper uses a variation of separation logic [29, 38] whose assertions separate access permissions from value information: separation logic’s points-to assertion is expressed as , and separation logic predicates [30] are similarly split into a predicate (abstracting over permissions) and a heap-dependent function (abstracting over values). Well-definedness checks ensure that the heap is accessed only under sufficient permissions. Viper provides a simple imperative language, which includes in particular two statements to manipulate the verification state: asserts all logical constraints in assertion A, removes the permissions in A from the current state (or fails if the permissions are not available) and assigns non-deterministic values to the corresponding memory locations (to reflect that the environment could now modify them); analogously assumes constraints and adds permissions.

Fig. 4.
figure 4

Excerpt of the Viper encoding of regions; general case (left), and for the lock region from Fig. 3 (right). The encoding function is denoted by double square brackets; overlines denote lists; foreach loops are expanded statically. Type T is the type of the state expression S, which is inferred. Actions A do not induce any global declarations. The elements of struct types and type are encoded as Viper references (type ). The expression temporarily unfolds a predicate into its definition; it is required by Viper’s backend verifiers. The struct type from Fig. 3 is encoded as a Viper reference with field (in Viper, all objects have all fields declared in the program).

Full size image

Regions and Assertions. TaDA’s regions introduce various resources such as region predicates and guards. We encode these into Viper permissions and predicates as summarized in Fig. 4 (left). Each region gives rise to a corresponding predicate, which is defined by the region interpretation. A region’s abstract state may be accessed by a Viper function , which is defined based on the region’s clause, and depends on the region predicate. Moreover, we introduce an abstract Viper predicate for each guard of the region.

These declarations allow us to encode most TaDA assertions in a fairly straightforward way. E.g. the assertion from Fig. 1 is encoded as a combination of a region predicate and the function yielding its abstract state: . We encode region identifiers as references in Viper, which allows us to use the permissions and values of designated fields to represent resources and information associated with a region instance. E.g. we use the permission to encode the TaDA resource .

figure bi

Rule Applications. Proof candidates are tree structures, where each premise of a rule application R is established as the conclusion of another rule application, as illustrated on the right. To check the validity of a candidate, we check the validity of each rule application. For rules that are natively supported by Viper (e.g. the assignment rule), Viper performs all necessary checks. Each other rule application is checked via an encoding into the following sequence of Viper instructions: (1) Exhale the precondition \(P_c\) of the conclusion to check that the required assertion holds. (2) Inhale the precondition \(P_p\) of the premise since it may be assumed when proving the premise. (3) After the code s of the premise, exhale the postcondition \(Q_p\) of the premise to check that it was established by the proof for the premise. (4) Inhale the postcondition \(Q_c\) of the conclusion. Steps 2 and 3 are performed for each premise of the rule. Moreover, we assert the side conditions of each rule. If a proof candidate is invalid, e.g. composes incompatible rules, one of the checks above fails and the candidate is rejected.

Using this encoding of rule applications as building blocks, we can assemble entire procedure proofs as follows: for each procedure, we inhale its precondition, encode the rule application for its body, and then exhale its postcondition.

Example: Stabilizing Assertions. Recall that an assertion A is stable if and only if the environment cannot invalidate A by performing any legal region updates. In practice, this means that the environment cannot hold a guard that allows it to change the state of a region in a way that violates A. The challenge of checking stability as a side-condition is to avoid higher-order quantification over region instances and guards, which is hard to automate. We address this challenge by eagerly stabilizing assertions in the Viper encoding, i.e. we weaken Viper’s verification state such that the remaining information about the state is stable. We achieve this effect by first assigning non-deterministic values to the region state and then constraining these to be within the states permitted by the region’s transition system, taking into account the guards the environment could hold. The Viper code for stabilizing instances of can be found in the full paper [47].

7 Evaluation

We evaluated Voila on nine benchmark examples from Caper’s test suite, with the Treiber’s stack [41] variant BagStack being the most complex example, and report verification times and annotation overhead. Each example has been verified in two versions: a version with Caper’s comparatively weak non-atomic specifications, and another version with TaDA’s strong atomic specifications; see Sect. 8 for a more detailed comparison of Voila and Caper. An additional example, CounterCl, demonstrates the encoding of a custom guard algebra not supported in Caper (see the full paper [47]). To evaluate performance stability, we seeded four examples with errors in the loop invariant, procedure postcondition, code, and region specification, respectively. Our benchmark suite is relatively small, but each example involves nontrivial specifications. To the best of our knowledge, no other (semi-)automated tool is able to verify similarly strong specifications.

Fig. 5.
figure 5

Timings in seconds for successful (left table) and failing (right table) verification runs; lines of code (LOC) are given for Voila programs and exclude proof annotations. Stg/Wk denote strong/weak Voila specifications; Cpr abbreviates Caper. Programs include spin and ticket locks, counters (Ctr), and client programs (Cl) using the proven specifications. Errors (Err) were seeded in loop invariants (L), postconditions (P), code (C), and region specifications (R).

Full size image

Performance. Figure 5 shows the runtime for each example in seconds. All measurements were carried out on a Lenovo W540 with an Intel Core i7-4800MQ and 16 GB of RAM, running Windows 10 x64 and Java HotSpot JVM 18.9 x64; Voila was compiled using Scala 2.12.7. We used a recent checkout of Viper and Z3 4.5.0 x64 (we failed to compile Caper against newer versions of Z3). Each example was verified ten times (on a continuously-running JVM); after removing the highest and lowest measurement, the remaining eight values were averaged. Caper (which compiles to native code) was measured analogously.

Overall, Voila’s verification times are good; most examples verify in under five seconds. Voila is slower than Caper and its logic-specific symbolic execution engine, but it exhibits stable performance for successful and failing runs, which is crucial in the common case that proof outlines are developed interactively, such that the checker is run frequently on incorrect versions. As demonstrated by the error-seeded versions of TLockCl and BagStack, Caper’s performance is less stable.

Another interesting observation is that strong specifications typically do not take significantly longer to verify, although only they require the full spectrum of TaDA ingredients and make use of TaDA’s most complex rules, MakeAtomic and UpdateRegion. Notable exceptions are: BagStack, where only the strong specification requires sequence theory reasoning; and TLock and BoundedCtr, whose complex transition systems with many disjunctions significantly increase the workload when verifying atomicity rules such as MakeAtomic.

Automation. Voila’s annotation overhead, averaged over the programs with strong specifications from Fig. 5, is 0.8 lines of proof annotations (not counting declarations and procedure specifications; neither for Caper) per line of code, which demonstrates the high degree of automation Voila achieves. Caper has an average annotation overhead of 0.13 for its programs from Fig. 5, but significantly weaker specifications. Verifying only the latter in Voila does not reduce annotation overhead significantly since Voila was designed to support TaDA’s strong specifications. The overhead reported for encodings into interactive theorem provers such as Coq [10, 17, 18, 45] is typically much higher, ranging between 10 and 20.

8 Related Work

We compare Voila to three groups of tools: automated verifiers, focusing on automation; proof checkers, focusing on expressiveness; and proof outline checkers, designed to strike a balance between automation and expressiveness. Closest to our work in the kind of supported logic is the automated verifier Caper [8], from which we drew inspiration, e.g. for how to specify region transition systems. Caper supports an improved version of CAP [7], a predecessor logic of TaDA. Caper’s symbolic execution engine achieves an impressive degree of automation, which, for more complex examples, is higher than Voila’s. Caper’s automation also covers slightly more guard algebras than Voila. However, the automation comes at the price of expressiveness, compared to Voila: postconditions are often significantly weaker because the logic does not support linearizability (or any other notion of abstract atomicity). E.g. Caper cannot prove that the spinlock’s procedure actually releases the lock. As was shown in Sect. 7, Caper is typically faster than Voila, but exhibits less stable performance when a program or its specifications are wrong.

Other automated verifiers for fine-grained concurrency reasoning are SmallfootRG [5], which can prove memory safety, but not functional correctness, and CAVE [44], which can prove linearizability, but cannot reason about non-linearizable code (which TaDA and Voila can). VerCors [26] combines a concurrent separation logic with process-algebraic specifications; special program annotations are used to relate concrete program operations to terms in the abstract process algebra model. Reasoning about the resulting term sequences is automated via model checking, but is non-modular. Summers et al. [39] present an automated verifier for the RSL family of logics [9, 10, 45] for reasoning about weak-memory concurrency. Their tool also encodes into Viper and requires very few annotations because proofs in the RSL logics are more stylized than in TaDA.

A variety of complex separation logics [9, 10, 12, 16, 19, 23, 37, 43, 45] are supported by proof checkers, typically via Coq encodings. As discussed in the introduction, such tools strike a different trade-off than proof outline checkers: they provide foundational proofs, but typically offer little automation, which hampers experimenting with logics.

Starling [46] is a proof outline checker and closest to Voila in terms of the overall design, but it focuses on proofs that are easy to automate. To achieve this, it uses a simple instantiation of the Views meta-logic [6] as its logic. Starling’s logic does not enable the kind of strong, linearizability-based postconditions that Voila can prove (see the discussion of Caper above). Starling generates proof obligations that can be discharged by an SMT solver, or by GRASShopper [31] if the program requires heap reasoning. The parts of an outline that involve the heap must be written in GRASShopper’s input language. In contrast, Voila does not expose the underlying system, and users can work on the abstraction level of TaDA.

VeriFast [14] can be seen as an outline checker for a separation logic with impressive features such as higher-order functions and predicates. It has no dedicated support for fine-grained concurrency, but the developers manually encoded examples such as concurrent stacks and queues. VeriFast favors expressiveness over automation: proofs often require non-trivial specification adaptations and substantial amounts of ghost code, but the results typically verify quickly.

9 Conclusion

We introduced Voila, a novel proof outline checker that supports most of TaDA’s features, and achieves a high degree of automation and good performance. This enables concise proof outlines with a strong resemblance of TaDA.

Voila is the first deductive verifier that can reason automatically about a procedure’s effect at its linearization point, which is essential for a wide range of concurrent programs. Earlier work either proves much weaker properties (the preservation of basic data structure invariants rather than the functional behavior of procedures) or requires substantially more user input (entire proofs rather than concise outlines).

We believe that our systematic approach to developing Voila can be generalized to other complex logics. In particular, encoding proof outlines into an existing verification framework allows one to develop proof outline checkers efficiently, without developing custom proof search algorithms. Our work also illustrates that an intermediate verification language such as Viper is suitable for encoding a highly specialised program logic such as TaDA. During the development of Voila, we uncovered and fixed several soundness and modularity issues in TaDA, which the original authors acknowledged and had partly not been aware of. We view this as anecdotal evidence of the benefits of tool support that we described in the introduction.

Voila supports the vast majority of TaDA’s features; most of the others can be supported with additional annotations. The main exception are TaDA’s hybrid assertions, which combine atomic and non-atomic behavior. Adding support for those is future work. Other plans include an extension of the supported logic, e.g. to handle extensions of TaDA [11, 36].