Statistical Properties of Exclusive and Non-exclusive Online Randomized Experiments Using Bucket Reuse

Abstract

Randomized experiments is a key part of product development in the tech industry. It is often necessary to run programs of exclusive experiments, i.e., groups of experiments that cannot be run on the same units during the same time. These programs imply restrictions on the random sampling, as units that are currently in an experiment cannot be sampled into a new one. Moreover, to technically enable this type of coordination with large populations, the units in the population are often grouped into ‘buckets’ and sampling is then performed on the bucket level. This paper investigates statistical implications of both the restricted sampling and the bucket-level sampling. The contribution of this paper is threefold: First, bucket sampling is connected to the existing literature on randomized experiments in complex sampling designs which enables establishing properties of the difference-in-means estimator of the average treatment effect. These properties are needed for inference to the population under random sampling of buckets. Second, the bias introduced by restricting the sampling as imposed by programs of exclusive experiments, is derived. Finally, practical recommendations on how to empirically evaluate and handle this bias is discussed together with simulations that support the theoretical findings .

M. Schultzberg—The authors thanks Andreas Born, Claire Detilleux, Brian St Thomas, Michael Stein, and the colleagues in the experimentation platform team for helpful feedback and suggestions for this paper.

Appendices

Appendix

All theorems are repeated here for convenience.

1.1 6.1 Complete Random Sampling of Buckets

Theorem 4

Under random sampling of equally sized buckets, with random treatment assignment into two equally sized groups, the sample difference-in-means estimator is an unbiased estimator of the ATE. i.e.

$$\begin{aligned} E[\widehat{ATE}] = ATE, \end{aligned}$$

where expectation is taken over the design space of random samples and treatment allocations.

Proof

Under random sampling of equally sized buckets, it follows that $\pi _i=\frac{N_S}{N}\,\,\forall \,\, i=1,...,N$, which implies that the Horvitz-Thompson estimator simplifies as

$$\begin{aligned} \hat{\bar{Y}}_{\pi _w}^w=\frac{N_S}{N \frac{N_S}{2}} \frac{N}{N_S} \sum _{i\in S_s} Y_i(W=w)=\frac{1}{\frac{N_S}{2}}\sum _{i\in S_s} Y_i(W=w)=\bar{Y}^w, \end{aligned}$$

(8)

which is simply the sample means of the groups. Unbiasedness follows directly from the results in [6], but we give an alternative proof here to build intuition. We drop the superscript t on the ATE to easy notation. Denote the difference-in-means estimator of the average treatment effect

$$\begin{aligned} \widehat{ATE}= \frac{1}{N_s/2} \left( \sum _{i:i\in \mathbf {S}\cap W_i=1} Y_i(W_i) -\sum _{i:i\in \mathbf {S}\cap W_i=0} Y_i(W_i) \right) . \end{aligned}$$

(9)

Enumerate all possible sample under random sampling of buckets with $\mathbf {S}_s$ where $s=1,...,\text {card}(\mathcal {S}_B)$. Moreover, enumerate all possible treatment assignments over random treatment assignments by $W^j$ where $j=1,...,\text {card}(\mathcal {W})$. This implies that we can write one single estimate as

$$\begin{aligned} \widehat{ATE}_{s,j}= \frac{1}{N_s/2} \left( \sum _{i:i\in \mathbf {S}_s\cap W^j_i=1} Y_i(W_i^j) -\sum _{i:i\in \mathbf {S}_s\cap W^j_i=0} Y_i(W_i^j) \right) . \end{aligned}$$

(10)

The expected value of $\widehat{ATE}_B$, where the subscript B indicates random sampling of buckets from $\mathcal {B}$, is given by

$$\begin{aligned} E[\widehat{ATE}_B]&= \frac{1}{\text {card}(\mathcal {S}_B)} \sum _{s=1}^{\text {card}(\mathcal {S}_B)}\left( \frac{1}{\text {card}(\mathcal {W})} \sum _{j=1}^{\text {card}(\mathcal {W})} \widehat{ATE}_{s,j} \right) \\&= \frac{1}{\text {card}(\mathcal {S}_B)} \frac{1}{\text {card}(\mathcal {W})} \sum _{s=1}^{\text {card}(\mathcal {S}_B)} \sum _{j=1}^{\text {card}(\mathcal {W})} \widehat{ATE}_{s,j} \\&= \frac{1}{\text {card}(\mathcal {S}_B)} \frac{1}{\text {card}(\mathcal {W})} \frac{2}{N_S} \left( {\sum _{s=1}^{\text {card}(\mathcal {S}_B)} \sum _{j=1}^{\text {card}(\mathcal {W})} \sum _{i:i\in \mathbf {S}_s\cap W^j_i=1} Y_i(W_i^j)} \right. \\&\left. -\,\sum _{s=1}^{\text {card}(\mathcal {S}_B)} \sum _{j=1}^{\text {card}(\mathcal {W})} \sum _{i:i\in \mathbf {S}_s\cap W^j_i=0} Y_i(W_i^j) \right) , \end{aligned}$$

where the last step follows from equally sized buckets. Due to the symmetry of the random sampling of buckets and the equal bucket size, each bucket (and thereby unit) will be in equally many samples. Moreover, in each sample, each unit is in the treatment and control groups equally many times, respectively, due to the mirror property of randomization distributions [8, 16]. This implies that we are simply adding and subtracting the value of each unit several times. It follows that

$$\begin{aligned} E[\widehat{ATE}_B]&= \frac{1}{\text {card}(\mathcal {S}_B)} \frac{1}{\text {card}(\mathcal {W})} \frac{2}{N_S} \left( \sum _{s=1}^{\text {card}(\mathcal {S}_B)} \sum _{j=1}^{\text {card}(\mathcal {W})} \sum _{i:i\in \mathbf {S}_s\cap W^j_i=1} Y_i(W_i^j) \right. \\&\left. -\sum _{s=1}^{\text {card}(\mathcal {S}_B)} \sum _{j=1}^{\text {card}(\mathcal {W})} \sum _{i:i\in \mathbf {S}_s\cap W^j_i=0} Y_i(W_i^j) \right) \\&= \frac{1}{\text {card}(\mathcal {S}_B)} \frac{1}{\text {card}(\mathcal {W})} \frac{2}{N_S} \left( \xi _B \sum _{i=1}^N Y_i(1) -\xi _B \sum _{i=1}^N Y_i(0) \right) . \end{aligned}$$

The number of time that each unit will be in the control and the treatment group across all possible samples and treatment assignments is given by

$$\begin{aligned} \xi _B&= \frac{\text {card}(\mathcal {W})}{2} \times \left( {\begin{array}{c}B-1\\ \frac{N_S}{N_B}-1\end{array}}\right) , \end{aligned}$$

which implies

$$\begin{aligned} E[\widehat{ATE}_B]&= \frac{1}{\text {card}(\mathcal {S}_B)} \frac{\left( {\begin{array}{c}K-1\\ \frac{N_S}{N_B}-1\end{array}}\right) }{N_S} \left( \sum _{i=1}^N Y_i(1) -\sum _{i=1}^N Y_i(0) \right) . \end{aligned}$$

We note that

$$\begin{aligned} \text {card}(\mathcal {S}_B) = \frac{B}{\frac{N_S}{N_B}} \left( {\begin{array}{c}B-1\\ \frac{N_S}{N_B}-1\end{array}}\right) \end{aligned}$$

which gives the final expression

$$\begin{aligned} E[\widehat{ATE}_B]&= \frac{N_S}{N_B B\left( {\begin{array}{c}K-1\\ \frac{N_S}{N_B}-1\end{array}}\right) } \frac{\left( {\begin{array}{c}K-1\\ \frac{N_S}{N_B}-1\end{array}}\right) }{N_S} \left( \sum _{i=1}^N Y_i(1) -\sum _{i=1}^N Y_i(0) \right) \\&= \frac{1}{N_B B} \left( \sum _{i=1}^N Y_i(1) -\sum _{i=1}^N Y_i(0) \right) \\&= \frac{1}{N} \left( \sum _{i=1}^N Y_i(1) -\sum _{i=1}^N Y_i(0) \right) =ATE. \end{aligned}$$

Which is in line with [6] as expected. $\blacksquare$

1.2 Restricted Random Sampling of Buckets

Lemma 2

For a $\delta _{\,\,\perp \!\!\! \perp }$ fulfilling Condition 1, the the difference in means estimator $\widehat{ATE^{\tilde{\mathcal {B}}_t}_{t-\delta _{\,\,\perp \!\!\! \perp }}}$ is an unbiased estimator of $ATE_{t-\delta _{\,\,\perp \!\!\! \perp }}$, i.e.,

$$\begin{aligned} E[\widehat{ATE^{\tilde{\mathcal {B}}_t}_{t-\delta _{\,\,\perp \!\!\! \perp }}}] = ATE_{t-\delta _{\,\,\perp \!\!\! \perp }} \end{aligned}$$

(11)

Proof

Since a program of exclusive experiment is expected to change user behaviour and therefore reactions to future changes, it generally holds that

(12)

However, it is also the case that the only dependency between the potential outcomes and the set of available buckets is captured by the history of the available buckets. The samples are random from the set of available buckets – if different subsets have different experiences that affects their behaviour such that the ATE changes, the dependency between the sample and these changes are completely described by the history of $\tilde{\mathcal {B}}_t$. It follows from Condition 1 that

$$\begin{aligned} \tilde{\mathcal {B}}_t \,\,\perp \!\!\! \perp \tilde{\mathcal {B}}_{t-\delta }, \tilde{\mathcal {B}}_{t-\delta -1},...,\tilde{\mathcal {B}}_{1} \Rightarrow Y_{t-\delta _{\,\,\perp \!\!\! \perp }}(0), Y_{t-\delta _{\,\,\perp \!\!\! \perp }}(1) \,\,\perp \!\!\! \perp \tilde{\mathcal {B}}_t. \end{aligned}$$

(13)

In other words, in relation to the potential outcomes at time $t-\delta _{\,\,\perp \!\!\! \perp }$, the subset $\tilde{\mathcal {B}}_t$ is a random subset from $\mathcal {B}$. One way to understand this is that from a randomization perspective it is equivalent to 1. randomly selecting a subset at time t, randomly sample from that subset, and finally randomly assign the treatment, and, 2. semi-randomly selecting subsets in steps until the subset is independent from the starting set (at step $\delta _{\,\,\perp \!\!\! \perp }$), and then sample and assign treatment randomly. The semi-random subsetting in $\delta _{\,\,\perp \!\!\! \perp }$ steps is essentially an ineffective method for randomly drawing a subset. The important practical difference between 1 and 2 is that in a program of exclusive experiments, the potential outcomes are expected to change as a function of the steps of subsetting in 2. For this reason, performing 1 at time t yields a subset that is independent of the outcome at time t and all other time periods, whereas 2 yields a subset that is independent in relation to the potential outcomes only at time $t-\delta _{\,\,\perp \!\!\! \perp }$ and before that.

Since $\tilde{\mathcal {B}}_t$ is a random subset of buckets in relation to the potential outcomes at time $t-\delta _{\,\,\perp \!\!\! \perp }$ under Condition 1, it only remains to prove that the difference-in-means estimator is an unbiased estimator of $ATE_{t-\delta _{\,\,\perp \!\!\! \perp }}$ under random ‘sampling’ of a subset, random sampling within the subset and random treatment assignment within the sample to prove Lemma 1. Enumerate the possible subsets,$\tilde{\mathcal {B}}_t^b$, of a given size as $b=1,...,\left( {\begin{array}{c}B\\ \text {card}(\tilde{\mathcal {B}}_t)\end{array}}\right)$, where each subset is equally probable in relation to the potential outcomes at time $t-\delta _{\,\,\perp \!\!\! \perp }$. In each subset, enumerate all possible samples $\mathbf {S}_s$ as $s=1,...,\left( {\begin{array}{c}\text {card}(\tilde{\mathcal {B}}_t)\\ \frac{N_S}{N_B}\end{array}}\right)$. This implies that using results from the proof of Theorem 1

$$\begin{aligned} E[\widehat{ATE^{\tilde{\mathcal {B}}_t}_t}]&= \frac{1}{\left( {\begin{array}{c}B\\ \text {card}(\tilde{\mathcal {B}}_t)\end{array}}\right) } \sum _{b=1}^{\left( {\begin{array}{c}B\\ \text {card}(\tilde{\mathcal {B}}_t)\end{array}}\right) } \frac{1}{\text {card}(\mathcal {S}_{\tilde{\mathcal {B}}^b_t})} \frac{1}{\text {card}(\mathcal {W})} \frac{2}{N_S} \\ {}&\left( \sum _{s=1}^{\text {card}(\mathcal {S}_{\tilde{\mathcal {B}}^b_t})} \sum _{j=1}^{\text {card}(\mathcal {W})} \sum _{i:i\in \mathbf {S}_s\cap W^j_i=1} Y_{i,t-\delta _{\,\,\perp \!\!\! \perp }}(W_i^j) \right. \\&\left. -\sum _{s=1}^{\text {card}(\mathcal {S}_B)} \sum _{j=1}^{\text {card}(\mathcal {W})} \sum _{i:i\in \mathbf {S}_s\cap W^j_i=0} Y_{i, t-\delta _{\,\,\perp \!\!\! \perp } }(W_i^j) \right) \\&= \frac{1}{\left( {\begin{array}{c}B\\ \text {card}(\tilde{\mathcal {B}}_t)\end{array}}\right) } \frac{1}{\text {card}(\mathcal {S}_{\tilde{\mathcal {B}}_t})} \frac{1}{\text {card}(\mathcal {W})} \frac{2}{N_S} \\&\left( \sum _{b=1}^{\left( {\begin{array}{c}B\\ \text {card}(\tilde{\mathcal {B}}_t)\end{array}}\right) } \sum _{s=1}^{\text {card}(\mathcal {S}_{\tilde{\mathcal {B}}^b_t})} \sum _{j=1}^{\text {card}(\mathcal {W})} \sum _{i:i\in \mathbf {S}_s\cap W^j_i=1} Y_{i,t-\delta _{\,\,\perp \!\!\! \perp }}(W_i^j) \right. \\&\left. - \sum _{b=1}^{\left( {\begin{array}{c}B\\ \text {card}(\tilde{\mathcal {B}}_t)\end{array}}\right) } \sum _{s=1}^{\text {card}(\mathcal {S}_B)} \sum _{j=1}^{\text {card}(\mathcal {W})} \sum _{i:i\in \mathbf {S}_s\cap W^j_i=0} Y_{i, t-\delta _{\,\,\perp \!\!\! \perp } }(W_i^j) \right) \end{aligned}$$

where, similar to the proof of Theorem 1, each unit is included in equally many subsets and samples, and within each sample each unit is included in the treatment group and the control group equally many times. It follows that

$$\begin{aligned} E[\widehat{ATE^{\tilde{\mathcal {B}}_t}_t}]&= \frac{1}{\left( {\begin{array}{c}B\\ \text {card}(\tilde{\mathcal {B}}_t)\end{array}}\right) } \frac{1}{\text {card}(\mathcal {S}_{\tilde{\mathcal {B}}_t})} \frac{1}{\text {card}(\mathcal {W})} \frac{2}{N_S} \left( \tilde{\xi } \sum _{i=1}^N Y_{i, t-\delta _{\,\,\perp \!\!\! \perp } }(1) -\tilde{\xi }\sum _{i=1}^N Y_{i, t-\delta _{\,\,\perp \!\!\! \perp } }(0) \right) , \end{aligned}$$

where

$$\begin{aligned} \tilde{\xi } = \frac{\text {card}(\mathcal {W})}{2} \times \left( {\begin{array}{c}\text {card}(\tilde{\mathcal {B}}_t)-1\\ \frac{N_S}{N_B}-1\end{array}}\right) \times \left( {\begin{array}{c}B-1\\ \text {card}(\tilde{\mathcal {B}}_t)-1\end{array}}\right) . \end{aligned}$$

(14)

Note that

$$\begin{aligned} \text {card}(\mathcal {S}_{\tilde{\mathcal {B}}_t})&= \frac{\text {card}(\tilde{\mathcal {B}}_t)}{\frac{N_S}{N_B}} \left( {\begin{array}{c}\text {card}(\tilde{\mathcal {B}}_t)-1\\ \frac{N_S}{N_B}-1\end{array}}\right) \\ \left( {\begin{array}{c}B\\ \text {card}(\tilde{\mathcal {B}}_t)\end{array}}\right)&= \frac{B}{\text {card}(\tilde{\mathcal {B}}_t)}\left( {\begin{array}{c}B-1\\ \text {card}(\tilde{\mathcal {B}}_t)-1\end{array}}\right) . \end{aligned}$$

Putting this together it follows that

$$\begin{aligned} E[\widehat{ATE^{\tilde{\mathcal {B}}_t}_t}]&= \frac{1}{\left( {\begin{array}{c}B\\ \text {card}(\tilde{\mathcal {B}}_t)\end{array}}\right) } \frac{1}{\text {card}(\mathcal {S}_{\tilde{\mathcal {B}}_t})} \frac{1}{\text {card}(\mathcal {W})} \frac{2}{N_S} \left( \sum _{i=1}^N Y_{i, t-\delta _{\,\,\perp \!\!\! \perp } }(1) -\sum _{i=1}^N Y_{i, t-\delta _{\,\,\perp \!\!\! \perp } }(0) \right) \\&=\frac{1}{\frac{B}{\text {card}(\tilde{\mathcal {B}}_t)}} \frac{1}{\frac{\text {card}(\tilde{\mathcal {B}}_t)}{\frac{N_S}{N_B}} } \frac{1}{N_S} \left( \sum _{i=1}^N Y_{i, t-\delta _{\,\,\perp \!\!\! \perp } }(1) -\sum _{i=1}^N Y_{i, t-\delta _{\,\,\perp \!\!\! \perp } }(0) \right) \\&=\frac{1}{N_BB} \left( \sum _{i=1}^N Y_{i, t-\delta _{\,\,\perp \!\!\! \perp } }(1) -\sum _{i=1}^N Y_{i, t-\delta _{\,\,\perp \!\!\! \perp } }(0) \right) \\&=\frac{1}{N} \left( \sum _{i=1}^N Y_{i, t-\delta _{\,\,\perp \!\!\! \perp } }(1) -\sum _{i=1}^N Y_{i, t-\delta _{\,\,\perp \!\!\! \perp } }(0) \right) =ATE_{t-\delta _{\,\,\perp \!\!\! \perp }}\,\, \blacksquare \end{aligned}$$

Theorem 5

For a $\delta _{\,\,\perp \!\!\! \perp }$ fulfilling condition 1, the bias in the difference in means estimator caused by sampling from the restricted set of the population of buckets given by $\tilde{\mathcal {B}}$ is given by

$$\begin{aligned} ATE- E[\widehat{ATE^{\tilde{\mathcal {B}}_t}_t}]&= \widetilde{ATE}_{t-\delta _{\,\,\perp \!\!\! \perp }:t} - \widetilde{ATE}^{ \tilde{\mathcal {B}}_t}_{t-\delta _{\,\,\perp \!\!\! \perp }:t}. \end{aligned}$$

Proof

Note that from Definition 1 it follows that

$$\begin{aligned} ATE - E[\widehat{ATE^{\tilde{\mathcal {B}}}_t}]&= ATE_{t-\delta _{\,\,\perp \!\!\! \perp }}+\widetilde{ATE}_{t-\delta _{\,\,\perp \!\!\! \perp }:t} - ATE_{t-\delta _{\,\,\perp \!\!\! \perp }}^{ \tilde{\mathcal {B}}_t} + \widetilde{ATE}_{t-\delta _{\,\,\perp \!\!\! \perp }:t}^{ \tilde{\mathcal {B}}_t}. \end{aligned}$$

By Lemma 1 the difference-in-means estimator under random sampling of bucket from $\tilde{\mathcal {B}}_t$ is an unbiased estimator of $ATE_{t-\delta _{\,\,\perp \!\!\! \perp }}$ which implies that $ATE_{t-\delta _{\,\,\perp \!\!\! \perp }}^{ \tilde{\mathcal {B}}_t} = ATE_{t-\delta _{\,\,\perp \!\!\! \perp }}$ which directly gives

$$\begin{aligned} ATE - E[\widehat{ATE^{\tilde{\mathcal {B}}}_t}]&= ATE_{t-\delta _{\,\,\perp \!\!\! \perp }}+\widetilde{ATE}_{t-\delta _{\,\,\perp \!\!\! \perp }:t} - ATE_{t-\delta _{\,\,\perp \!\!\! \perp }} + \widetilde{ATE}_{t-\delta _{\,\,\perp \!\!\! \perp }:t}^{ \tilde{\mathcal {B}}_t}\\&= \widetilde{ATE}_{t-\delta _{\,\,\perp \!\!\! \perp }:t} - \widetilde{ATE}^{ \tilde{\mathcal {B}}_t}_{t-\delta _{\,\,\perp \!\!\! \perp }:t} \,\,\blacksquare \end{aligned}$$

Simulations

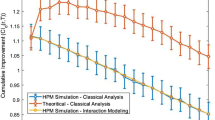
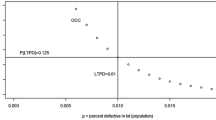
Here the simulation from Sect. 5.2 is repeated but with 100 buckets instead of 10000. All simulations can be replicated using the Julia code in the supplementary files. The parameters are repeated in Table 3 for convenience. Fig. 8 and 9 display the simulation results. The patterns are the same as in Sect. 5.2, but the biases are generally larger for the same settings when the number of buckets is smaller. This is expected, as the heterogeneity is ‘fixed’ between these settings, in the sense that the ATE’s for the first time points are drawn from the same normal distribution. This implies that there are going to be more and more buckets (when the number of buckets increase) with similar values, in turn implying that the heterogeneity between samples will decrease.

Table 3. Parameters of the Monte Carlo simulation. For parameters with lists of values, a value is randomly (uniformly) drawn when a new experiment is started.

Fig. 8.

The ATE1 bias, bucket availability correlation, and bucket sampling correlation plotted as a function of $\delta$, for settings 1–2. The parameters for each setting are given in Table 2.

Fig. 9.

The ATE1 bias, bucket availability correlation, and bucket sampling correlation plotted as a function of $\delta$, for settings 3–6. The parameters for each setting are given in Table 2.