Estimation of the Shear Strength of RC Members with Externally Bonded, Fully-Wrapped FRCM Composites

Abstract

Externally bonded (EB) fiber reinforced cementitious matrix (FRCM) composites have been proven to be an effective solution for shear strengthening existing reinforced concrete (RC) members. Different layouts, namely U- and full-wrapping, of the EB composite can be adopted depending on the geometry and type of RC member. In the case of RC beams, the fully-wrapped layout is not always possible due to the presence of the slab. However, this layout is particularly attractive in the case of RC columns, where the composite can be applied easily and may provide significant strength increase. Although FRCM composites are attracting interest, the availability of analytical design models is still quite limited. In particular, few studies regarding the evaluation of the shear strength of FRCM fully-wrapped RC members are available in the literature. In this paper, an analytical model for the estimation of the contribution of fully-wrapped FRCM composites to the shear strength of RC members is proposed. The model is based on the truss analogy commonly adopted by various codes and guidelines for the estimation of the shear strength of RC beams and for fiber reinforced polymer (FRP) strengthened RC beams. The analytical model estimates the contribution of the FRCM to the member shear strength accounting for the bond behavior of the specific composite employed, which is an important aspect since FRCM composites have reported different bond behavior than FRP composites externally bonded to concrete substrates. The accuracy of the model provisions is assessed by comparing analytical and experimental results of RC beams fully-wrapped with a carbon FRCM composite.

1 Introduction

Fiber reinforced cementitious matrix (FRCM) composites represent a potential strengthening solution for existing reinforced concrete (RC) and masonry members. They are comprised of high-strength fiber open mesh textiles embedded within inorganic matrixes (ACI 549.4R-13). FRCM composites are employed as externally bonded reinforcement to enhance the flexural, shear, and axial load-carrying capacity of RC and masonry members (Alecci et al. 2017, Babaeidarabad et al. 2014, D’Antino et al. 2018, Ombres and Verre 2019, Trapko et al. 2015). Although FRCMs provide a strength contribution that is generally lower than that of fiber reinforced polymer (FRP) composites with the same fiber cross-sectional area (Papanicolaou et al. 2008), they can be preferred to FRPs due to their good compatibility with the substrate, vapor permeability, and resistance to elevated temperatures (Koutas and Bournas 2019). Members strengthened with FRCM comprising one or two fiber layers generally fail due to debonding within the composite, at the matrix-fiber interface (Alecci et al. 2017). For this reason, the bond behavior of FRCM composites has been largely studied and analytical and numerical models were proposed (Focacci et al. 2017, Nerilli et al. 2020).

Although experimental and analytical research efforts were made to formulate reliable design procedures for FRCM strengthened RC beams subjected to flexure (Bencardino et al. 2018, D’Antino et al. 2020a), limited research has been done to investigate the FRCM contribution to the shear strength of RC beams (Gonzalez-Libreros et al. 2017). Two main reinforcement layouts can be adopted for shear strengthening of RC members: in the U-wrapped configuration, the reinforcement is wrapped around three sides of the cross-section, whereas in the fully-wrapped configuration the reinforcement is wrapped around the entire cross-section (ACI 549.4R-13). The limited available literature showed that using the fully-wrapped configuration allows for obtaining a higher contribution of the composite to the member shear strength with respect to that of the corresponding U-wrapped configuration (Gonzalez-Libreros et al. 2017, Tetta et al. 2015).

The shear strength V_u of RC members strengthened with externally bonded (EB) reinforcement is typically computed by adding the contribution V_f provided by the EB reinforcement to the shear strength V_un of the unstrengthened element (ACI 549.4R-13, ACI 440.2R-17, CNR-DT 200/R1 2013):

$$V_{u} = V_{un} + V_{f}$$

(1)

The Mörsch truss is generally employed to compute V_f. Accordingly, when a composite material is employed as EB reinforcement, V_f can be expressed as (D’Antino et al. 2020b):

$$V_{f} = 2n{\upsigma }_{fe} t_{f} d_{fe} \frac{{w_{f} }}{{i_{f} }}\left( {\cot {\uptheta } + \cot {\upbeta }} \right)\sin {\upbeta }$$

(2)

where n is the number of fiber layers, σ_fe is the composite effective stress, t_f is the fiber layer equivalent thickness, d_fe is the composite effective depth, w_f is the composite strip width, i_f is the strip center-to-center spacing measured orthogonal to the member longitudinal axis, and θ and β are the inclination angles of the concrete compressed strut and of the fiber with respect to the member longitudinal axis, respectively. Equation (2) assumes that failure occurs due to the opening of a main diagonal crack, for which the inclination coincides with the inclination θ of the compressed struts. Following these assumptions, the composite effective stress σ_fe is the average stress in the composite bridging the main diagonal crack. Equation (2) can be used independently of the composite layout, which affects the value of σ_fe. Analytical formulations to compute the effective stress of FRCM U-wrapped members were proposed in (D’Antino et al. 2020b). These formulations are based on available models for EB FRP reinforcement (see e.g. ACI 440.2R-17 and CNR-DT 200/R1 2013) and take into account the bond behavior of the specific FRCM considered, although they can be generalized since they explicitly account for the key parameters characterizing the shear stress-transfer at the reinforcement-substrate interface. In particular, the models were able to account for the presence of friction at the matrix-fiber interface that was observed in some FRCM composites (Nerilli et al. 2020).

In this paper, the approach adopted in D’Antino et al. (2020) for FRCM U-wrapped members is extended to the case of fully-wrapped members by deriving an analytical model to compute the effective stress σ_fe depending on the bond behavior of the specific FRCM composite considered. Since the model is based on the Mörsch truss, it can be adopted to compute the composite contribution to the member shear strength according to current FRCM design guidelines (ACI 549.4R-13 and CNR-DT 215/2018). The model is validated by comparing the experimental and corresponding analytical results of the carbon FRCM strengthened beams tested by Tetta et al. (2015).

2 Bond Behavior of FRCM Composites

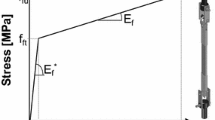
In this paper, matrix-fiber debonding failure is assumed. However, the analysis provided can be extended to any debonding failure mode according to the bond behavior observed (D’Antino et al. 2018). FRCM-concrete direct shear tests showed a peculiar bond behavior that allowed for identifying an idealized applied stress σ – global slip g response, where σ is the axial stress in the fiber textile, and g is the fiber-substrate relative displacement (i.e. the fiber slip), both measured at the composite loaded end (Focacci et al. 2017). Figure 1a shows the idealized load response of various FRCM-concrete joints with the same matrix-fiber interface fracture energy G_F and bonded length ℓ (see Fig. 1b and c), assumed to be longer than the composite effective bond length l_eff, i.e. the minimum length needed to fully develop the bond load-carrying capacity. Considering an FRCM-concrete joint (see sketch in Fig. 1c) that showed the presence of a friction shear stress τ_f at the matrix-fiber interface at the completion of the test, after an initial linear stage, the σ – g response is non-linear until the onset of debonding, which occurs at the applied stress σ_deb. After this stage, which is referred to as the bonded stage, the applied stress can further increase while the stress transfer zone (STZ), which is the matrix-fiber interface area where the bond shear stress is transferred, translates toward the free end. This stage, referred to as the partially debonded stage, ends when the STZ reaches the free end and the peak applied stress σ^* is attained. After this point, the applied stress decreases while a snap-back phenomenon occurs due to the recovering of the fiber elastic deformation (Fig. 1a) until a constant applied stress σ_f due to friction at the matrix-fiber interface is attained. Since σ_f is provided by friction only, it can be used to compute the friction shear stress τ_f:

$${\uptau }_{f} = \frac{{{\upsigma }_{f} A_{f} }}{{p_{f} \ell }}$$

(3)

where A_f = t_fw_f is the fiber cross-sectional area, t_f is the fiber equivalent thickness (i.e. the fiber thickness assumed to be spread uniformly across the composite width w_f), and p_f = 2w_f is the matrix-fiber contact perimeter.

If the composite free end is restrained, i.e. the free end slip s_F is always equal to 0, the applied stress can further increase after σ^* until the composite tensile strength σ_m is attained (see σ – g curve with stress τ_f ≠ 0 and s_F = 0 in Fig. 1a and the sketch in Fig. 1b). During this stage, which is referred to as the restrained stage, the slope of the σ – g curve approaches E_f/ℓ, where E_f is the fiber elastic modulus. Figure 1a also shows a load response for an FRCM-concrete joint without friction (τ_f = 0) and with restrained free end (s_F = 0). In this case, the applied stress remains constant after attaining σ_deb until the STZ reaches the free end and the applied stress starts to increase again. It should be noted that, although the fracture energy G_F is the same, the debonding stress of FRCM-concrete joints with and without friction are different since the presence of friction was assumed to provide a contribution to the interface capacity even during the bonded stage (D’Antino et al. 2020b). It should be noted that σ^* is defined as the maximum stress attained by the FRCM-substrate joint with bonded length ℓ without considering the effect of the restrained end (if present, see sketch Fig. 1c).

Fig. 1.

a) Applied stress σ – global slip g response of an FRCM-concrete joint with different frictional shear stress (τ_f) and free end restraint (s_F) conditions (τ_f ≠ 0 and s_F = 0; τ_f ≠ 0 and s_F ≠ 0; τ_f = 0 and s_F = 0). Sketch of an FRCM-concrete joint b) with and c) without restrained free end.

The σ – g response of an FRCM-concrete joint with bonded length ℓ and with τ_f ≠ 0 and s_F = 0 can be approximated by a stepwise function where σ₁(g) describes the bonded stage, σ₂(g) describes the partially debonded stage, and σ₃(g) describes the restrained stage:

$${\upsigma }(g) = \left\{ {\begin{array}{*{20}l} {{\upsigma }_{1} (g) = ag^{3} + bg^{2} + cg} \hfill & {g \le g_{deb} } \hfill \\ {{\upsigma }_{2} (g) = m_{g} \left( {g - g_{deb} } \right) + {\upsigma }_{deb} } \hfill & {g_{deb} < g \le g^{*} } \hfill \\ {{\upsigma }_{3} (g) = \frac{{E_{f} }}{\ell }\left( {g - g^{*} } \right) + {\upsigma }^{*} } \hfill & {g^{*} < g \le g_{m} } \hfill \\ \end{array} } \right.$$

(4)

where a, b, and c are coefficients that depend on the specific FRCM bond behavior, g_deb, g^*, and g_m are the global slips associated to σ_deb, σ^*, and σ_m, respectively (Fig. 1), and m_g is:

$$m_{g} = \frac{{2{\uptau }_{f} E_{f} p_{f} }}{{2{\upsigma }_{deb} A_{f} + p_{f} {\uptau }_{f} (\ell - l_{eff} )}}$$

(5)

where m_g is obtained assuming a linear behavior of the σ₂(g) function between g_deb and g^* (D’Antino et al. 2014). The coefficients a, b, and c can be calibrated i) by best fitting of σ – g curves obtained by FRCM-concrete joints with bonded length ℓ, ii) using inverse calibration methods such those proposed in (Focacci et al. 2017), or iii) by enforcing three boundary conditions on σ₁(g). Following the approach iii), a, b, and c can be obtained by enforcing (D’Antino et al. 2020b):

$$\left\{ {\begin{array}{*{20}l} {{\upsigma }_{1} (g_{deb} ) = {\upsigma }_{deb} } \hfill \\ {{\upsigma }_{1}^{\prime } (g_{deb} ) = m_{g} } \hfill \\ {{\upsigma }_{deb} = {\upsigma }_{b} \sqrt {\frac{{{\upsigma }_{deb}^{2} A_{f} }}{{{\upsigma }_{deb}^{2} A_{f} - E_{f} p_{f} g_{deb} {\uptau }_{f} }}} } \hfill \\ \end{array} } \right.$$

(6)

where σ_b is the bond stress provided by bond only, i.e. without considering the contribution of friction, at the onset of debonding (D’Antino et al. 2020b). Enforcing the conditions of Eq. (6) in Eq. (4), the coefficients are:

$$\left\{ {\begin{array}{*{20}l} {a = \frac{{m_{g} - c - 2bg_{deb} }}{{3g_{deb}^{2} }}} \hfill \\ {b = \frac{{3{\upsigma }_{deb} - 2g_{deb} c - m_{g} g_{deb} }}{{g_{deb}^{2} }}} \hfill \\ {c = m_{g} - \frac{{{\upsigma }_{deb} }}{{g_{deb} }}\left( {6 - 8{\upsigma }_{deb} \sqrt {\frac{{A_{f} }}{{{\upsigma }_{deb}^{2} A_{f} - E_{f} p_{f} g_{deb} {\uptau }_{f} }}} } \right)} \hfill \\ \end{array} } \right.$$

(7)

Equation (4) can be adopted to describe the load response of any FRCM-concrete joint with bonded length ℓ longer than l_eff. If ℓ ≤ l_eff, Eq. (4) can still be adopted without considering the branch σ₂(g) (the branch σ₃(g) is still present).

3 FRCM Shear Strength Contribution

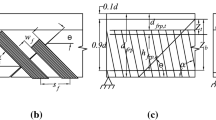
According to the truss analogy commonly adopted for estimating the shear strength of composite strengthened RC beams, the composite provides its contribution across a main shear crack with the tip located at the centroid of the flexural compression zone. Only the composite located between the crack tip and the centroid of the flexural tension reinforcement is considered. In general, for crack axis ξ with its origin at the crack tip, the crack opening is assumed to increase linearly with ξ, as a function of the crack opening angle α (Fig. 2a):

$$w\left(\upxi \right) = \upalpha \upxi$$

(8)

Although other crack shapes can be adopted, the linear crack shape is considered in this paper for consistency with available design models for U-wrapped FRCM reinforcement (D’Antino et al. 2020b). Assuming this crack shape, the available bonded length ℓ of a fully-wrapped FRCM composite crossing the main diagonal shear crack is (Monti and Liotta 2007):

$$\ell \left( y \right) = \left\{ {\begin{array}{*{20}l} {\frac{z - y}{{\sin {\upbeta }}}} \hfill & {0 \le y \le \frac{z}{2}} \hfill \\ {\frac{y}{{\sin {\upbeta }}}} \hfill & {\frac{z}{2} \le y \le z} \hfill \\ \end{array} } \right.$$

(9)

where y is the coordinate along the beam vertical axis with the origin in the crack tip (the y-axis is depicted in Fig. 2b, where the ℓ(y) function is also depicted). Figure 2a shows the stress σ(ξ) in the fiber of the composite strips crossing the main diagonal shear crack along the crack axis ξ. Provided a certain crack opening α, σ(ξ) depends on the available bonded length and on the slip g at the crack edge. Therefore, the overall force F_f provided by the composite crossing the crack is:

$$F_{f} = 2nt_{f} \mathop {\max }\limits_{\upalpha } \int_{0}^{{\upxi _{1} }} {\upsigma \left( {g,\ell } \right){\text{d}}\upxi }$$

(10)

where n is the number of fiber layers, and 2 accounts for the composite contribution on the two sides of the cross-section.

Fig. 2.

a) Stress distribution along the assumed main shear crack and b) available bonded length ℓ(y).

The integral in Eq. (10) depends on the value of α. In the case of U-wrapped members, the integral in Eq. (10) reaches the maximum value when the stress in the fibers attains simultaneously the peak stress σ^* along the entire crack length (Monti and Liotta 2007). However, in the case of fully-wrapped members, the maximum value of the integral in Eq. (10) is associated with the attainment of the composite tensile strength σ_m in one of the fibers crossing the crack. Depending on several parameters, such as the beam height, inclination of the fiber β and crack θ, and bond behavior of the specific composite considered, the location along the crack where σ_m is first attained may vary. In this paper, it is assumed that σ_m is first attained at the crack mid-length ξ_m = ξ₁/2 where the shortest bonded length is available (see Fig. 2b), which entails for a global slip g_m that is less than that associated to longer bonded lengths, and that the same stress σ_m is attained simultaneously by all fibers located between ξ_m and ξ₁ (Fig. 2a). This condition is associated with the maximum value of the integral in Eq. (10). The angle corresponding to this condition is named the critical crack opening angle α_cr:

$${\upalpha }_{cr} = \frac{{4g_{m} \left( {l_{m} } \right)}}{z}\frac{{\sin {\uptheta }}}{{\sin \left( {{\uptheta } + {\upbeta }} \right)}} \le {\upalpha }_{u} = \frac{{w_{u} \sin {\uptheta }}}{z}$$

(11)

where g_m(l_m) is the global slip corresponding to composite tensile strength at ξ_m, w_u is the crack opening (Fig. 2a) associated to a significant degradation of the shear strength provided by the concrete, and α_u is the corresponding crack opening angle. It should be noted that the limit α_u enforced on the critical crack opening angle α_cr has the same scope of the limit enforced on the composite maximum strain by the American guidelines for FRP and FRCM composites (ACI 549.4R-13, ACI 440.2R-17).

g_m(l_m) in Eq. (11) depends on the relationship between the bonded length l_m = z/(2senβ) associated with ξ_m and the composite effective bond length l_eff:

$$g_{m} \left( {l_{m} } \right)\left\{ {\begin{array}{*{20}l} {g_{deb} \left( {1 - \sqrt {1 - \frac{{{\upsigma }^{*} \left( {l_{m} } \right)}}{{{\upsigma }_{deb} }}} } \right) + \left[ {{\upsigma }_{m} - {\upsigma }^{*} \left( {l_{m} } \right)} \right]\frac{{l_{m} }}{{E_{f} }}} \hfill & {l_{m} \le l_{eff} } \hfill \\ {g_{deb} - \frac{1}{{E_{f} }}\left[ {{\upsigma }_{deb} l_{eff} + {\upsigma }_{m} l_{m} - (l_{m}^{2} - l_{eff}^{2} )\frac{{{\uptau }_{f} }}{{t_{f} }}} \right]} \hfill & {l_{m} > l_{eff} } \hfill \\ \end{array} } \right.$$

(12)

The composite peak stress σ^*(l_m) is (D’Antino et al. 2020b):

$${\upsigma }^{*} \left( {l_{m} } \right) = c_{l} l_{m} + \frac{{l_{m}^{3} \left( {c_{l} l_{eff} - 2{\upsigma }_{deb} + 2{\uptau }_{f} l_{eff} /t_{f} } \right)}}{{l_{eff}^{3} }} - \frac{{l_{m}^{2} \left( {2c_{l} l_{eff} - 3{\upsigma }_{deb} + 2{\uptau }_{f} l_{eff} /t_{f} } \right)}}{{l_{eff}^{2} }}$$

(13)

Since both σ₁(g) and σ^*(ℓ) can be approximated with cubic functions (D’Antino et al. 2020b), the coefficient c_l in Eq. (13) can be obtained by the third equation in Eq. (7) substituting g_deb with l_eff and imposing m_g = m = 2τ_f/t_f. It should be noted that the first equation in Eq. (12) was obtained considering a parabolic shape of the σ₁(g) curve rather than a cubic shape (see Eq. (4)) to obtain a simple closed-form solution.

Provided α_cr, the effective stress σ_fe,W for a fully-wrapped member can be obtained substituting Eq. (4) into Eq. (10) and considering that the effective stress is defined as the average composite stress along the main diagonal crack:

$$\upsigma _{fe,W} = \frac{{F_{f} }}{{2\upxi _{1} }} = \left\{ {\begin{array}{*{20}l} {\frac{1}{{{2}\upxi _{m} }}\left[ {\int_{0}^{{\upxi _{deb} }} {\upsigma _{1} \left(\upxi \right){\text{d}}\upxi } + \int_{{\upxi _{deb} }}^{{\upxi ^{*} }} {\upsigma _{2} \left(\upxi \right){\text{d}}\upxi } + \int_{{\upxi ^{*} }}^{{\upxi _{m} }} {\upsigma _{3} \left(\upxi \right){\text{d}}\upxi } { + }\upsigma _{m}\upxi _{m} } \right]} \hfill & {\upxi _{deb} \le\upxi ^{*} } \hfill \\ {\frac{1}{{{2}\upxi _{m} }}\left[ {\int_{0}^{{\upxi _{m} }} {\upsigma _{1} \left(\upxi \right){\text{d}}\upxi } { + }\upsigma _{m}\upxi _{m} } \right]} \hfill & {\upxi _{deb} >\upxi ^{*} } \hfill \\ \end{array} } \right.$$

(14)

where ξ_deb, ξ^*, and ξ_m are the crack lengths where the fiber attains σ_deb, σ^*, and σ_m, respectively. The closed-form solution of Eq. (14) is quite complex and difficult to use in practice. To obtain a simpler expression of the effective stress, the functions σ₂(g) and σ₃(g) in Eq. (4) were simplified in Eqs. (15) and (16) assuming ℓ = ℓ_m and ℓ = l_r, respectively, where ℓ_m = max{z/sin(β),l_eff}, and l_r < ℓ_m is a reference length that controls the slope of the σ-ξ curves associated to σ₃(g):

$$\upsigma _{2} (g) = m_{r} \left( {g - g_{deb} } \right) +\upsigma _{deb} = \frac{{2\uptau _{f} E_{f} p_{f} }}{{2\upsigma _{deb} A_{f} + p_{f}\uptau _{f} (\ell_{m} - l_{eff} )}}\left( {g - g_{deb} } \right) +\upsigma _{deb}$$

(15)

$$\upsigma _{3} (g) = \frac{{E_{f} }}{{l_{r} }}\left( {g - g^{*} } \right) +\upsigma ^{*}$$

(16)

Accordingly, m_g should also be set equal to m_r in Eqs. (4)-(7). It should be noted that adopting Eqs. (15) and (16) entails for a conservative estimation of σ_fe with respect to that obtained with the exact solution of Eq. (14). According to Eq. (16), when l_r → 0, σ₃(g) → ∞, which means that the stress in the fibers suddenly increases from σ^* to σ_m at ξ = ξ^* = ξ_m. Therefore, considering a small value of l_r results in an underestimation of the stress in the fibers associated to the restrained stage and, in turn, a conservative estimation of σ_fe,W. With the simplifications of Eqs. (15) and (16), Eq. (14) becomes:

$$\begin{gathered}\upsigma _{fe,Wr} = \hfill \\ \; = \left\{ {\begin{array}{*{20}l} {\frac{{\upxi _{deb}^{2} }}{{{2}\upxi _{m} }}\left[ {\frac{{3ak^{3}\upxi _{deb}^{2} + 4bk^{2}\upxi _{deb} + 6ck}}{12} + \frac{qk}{{2{\upxi }_{deb} }}\left( {\upxi _{deb} - 2\upxi _{m} } \right) - \frac{{\upsigma _{deb} }}{{\upxi _{deb} }}} \right] + \frac{{2\left( {\upsigma _{deb} +\upsigma _{m} } \right) + qk\upxi _{m} }}{4}} \hfill & {\upxi _{deb} \le\upxi ^{*} } \hfill \\ {\frac{{\upxi _{m} k}}{{{24}}}\left( {3ak^{3}\upxi _{m}^{2} + 4bk\upxi _{m} + 6c} \right) + \frac{{\upsigma _{m} }}{2}} \hfill & {\upxi _{deb} >\upxi ^{*} } \hfill \\ \end{array} } \right. \hfill \\ \end{gathered}$$

(17)

where σ_fe,Wr denotes the simplified formula of the effective stress and:

$$\upxi _{deb} = \frac{{2g_{deb} }}{{\upalpha _{cr} \sin (\uptheta +\upbeta )}}$$

(18)

$$\upxi ^{*} = \frac{{l_{r} (\upsigma _{m} -\upsigma _{deb} + qk\upxi _{deb} ) - E_{f} k\upxi _{m} }}{{qkl_{r} - E_{f} k}}$$

(19)

$$\upxi _{m} = \frac{z}{{2\sin\uptheta }}$$

(20)

$$k = \frac{{\upalpha _{cr} }}{2}\sin (\uptheta +\upbeta )$$

(21)

$$q = \frac{{2\uptau _{f} E_{f} p_{f} \sin\upbeta }}{{{2}\upsigma _{deb} A_{f} \sin\upbeta { + }\uptau _{f} p_{f} (z - l_{eff} \sin\upbeta )}}$$

(22)

Equation (17) provides the effective stress for FRCM composites that show the presence of friction at the matrix-fiber interface. For FRCMs that do not show the presence of friction, i.e. τ_f = 0 (see Fig. 1), Eq. (17) becomes:

$$\upsigma _{fe,Wr2} = \left\{ {\begin{array}{*{20}l} {\frac{{\upsigma _{deb} +\upsigma _{m} }}{2} - \frac{{g_{deb} \sin\uptheta {(6}\upsigma _{deb} - cg_{deb} {)}}}{{6az\sin ({\uptheta } + {\upbeta })}}} \hfill & {\upxi _{deb} \le\upxi ^{*} } \hfill \\ {\frac{j}{{1536g_{deb}^{3} }}\left\{ {96cg_{deb}^{3} + j\left[ {\upsigma _{deb} (48g_{deb} - 6j) + cg_{deb} (3j - 32g_{deb} )} \right]} \right\} + \frac{{\upsigma _{m} }}{2}} \hfill & {\upxi _{deb} >\upxi ^{*} } \hfill \\ \end{array} } \right.$$

(23)

where σ_fe,Wr2 denotes the effective stress obtained by the simplified formula without considering the contribution of friction and:

$$j = \frac{{\upalpha _{cr} z\sin (\uptheta +\upbeta )}}{{\sin\uptheta }}$$

(24)

It should be noted that the model described above does not account for the presence of stress concentration at the cross-section corner due to the lack of experimental results able to describe the variation of the maximum stress attained by the composite for different corner radii. Further analyses are needed to clarify the effect of this phenomenon, which was observed to have an important effect on the composite maximum stress of fully-wrapped FRP composites (Monti and Liotta 2007).

4 Comparison Between U-wrapped and Fully-Wrapped Configurations

The effective stress associated with an FRCM composite U-wrapped around a RC member can be estimated as (D’Antino et al. 2020b):

$$\upsigma _{fe,U3} = \left\{ {\begin{array}{*{20}l} {L_{max} \left[ {\left( {\frac{{L_{max} }}{2}} \right)^{2} \frac{{l_{eff} \left( {c_{l} + m} \right) - 2\upsigma _{deb} }}{{l_{eff}^{3} }} + \frac{{L_{max} }}{3}\frac{{3\upsigma _{deb} - l_{eff} \left( {2c_{l} + m} \right)}}{{l_{eff}^{2} }} + \frac{{c_{l} }}{2}} \right]} \hfill & {L_{max} < l_{eff} < l_{max,3} } \hfill \\ {\frac{1}{{L_{max} }}\left\{ {\left[ {\upsigma _{deb} + \frac{m}{2}\left( {L_{max} - l_{eff} } \right)} \right]\left( {L_{max} - l_{eff} } \right) + l_{eff} \frac{{{6}\upsigma _{deb} + l_{eff} \left( {c_{l} - m} \right)}}{12}} \right\}} \hfill & {L_{max} < l_{eff} < l_{max,3} } \hfill \\ \end{array} } \right.$$

(25)

where L_max = min{z,d_f}/sin(β), m = p_fτ_f/A_f, and l_max,₃ is the bonded length needed to attain the composite tensile strength. σ_fe,U3 shall be limited to the effective stress corresponding to the attainment of the composite tensile strength.

Equations (14), (17), and (25) are used in this section first to evaluate the error made by considering the simplified effective stress with respect to that obtained by the closed-form solution, and then to evaluate the theoretical increase of the effective stress of the fully-wrapped configuration with respect to the corresponding U-wrapped configuration with strips extending up to the crack tip. The comparisons are made considering a PBO FRCM composite for which the parameters needed were reported in the literature (D’Antino et al. 2014): l_eff = 260 mm, σ_deb = 1908 MPa, t_f = 0.046 mm, s_f = 1.57 mm, and E_f = 206 GPa. This specific FRCM showed the presence of friction (τ_f was reported to be 0.03 MPa (Focacci et al. 2017)). To investigate the effect of friction on the effective stress, τ_f was assumed equal to 0, 0.01, 0.02, 0.04, and 0.06 MPa in the analysis. The RC member inner lever arm considered was z = 300 mm or 600 mm, and a PBO FRCM tensile strength σ_m = 2500 MPa or 3015 MPa was adopted. The concrete compressive strut and fiber inclination angles were assumed θ = 45° and β = 90°. Finally, the crack opening angle α_cr was not limited to α_u.

Figure 3a shows the comparison between σ_fe,Wr and σ_fe,W for the parameters considered. The results show that adopting the simplified formulation leads to a small underestimation (maximum underestimation lower than 4%) of the effective stress with respect to the closed-form solution, and that increasing the z decreases the difference between σ_fe,Wr and σ_fe,W, whereas increasing σ_m increases it.

Fig. 3.

a) Comparison between the effective stress of fully-wrapped members obtained by the simplified and closed-form solution of Eq. (14). b) Comparison between the effective stress of fully-wrapped members obtained by the simplified solution of Eq. (14) and that of corresponding U-wrapped members.

Figure 3b shows the comparison between σ_fe,Wr and σ_fe,U3 for the same parameters considered in Fig. 3a The results show that using the fully-wrapped configuration may improve the effective stress up to almost 60% with respect to the effective stress of the U-wrapped configuration. However, this improvement depends on the member geometry and composite bond behavior and tensile strength. Furthermore, for large values of z, the crack opening angle should be limited by α_u to provide an acceptable degradation of the shear strength provided by concrete. For z = 600 mm, the presence of high friction stress τ_f increases the effective stress in the U-wrapped configuration at a higher rate than in the fully-wrapped configuration, which is responsible for the downward trend observed for z = 600 mm in Fig. 3b. This effect may also lead to small improvement of the shear strength contribution from the U-wrapped to the fully-wrapped configuration in certain applications.

5 Comparison Between Analytical and Experimental Results

The analytical model proposed was applied to predict the composite shear strength contribution of RC beams fully-wrapped with FRCM. A limited number of studies, sometimes with contradictory results, is available in the literature regarding FRCM fully-wrapped RC members (Gonzalez-Libreros et al. 2017). In this paper, the results provided by Tetta et al. (2015) were considered. Five rectangular RC beams were strengthened with a U-wrapped (3 beams, named UW_Mn, where n = 1, 2, or 3 is the number of textile layers) and fully-wrapped (2 beams, named FW_Mn, where n = 1 or 2 is the number of textile layers) carbon FRCM. All beams considered failed in shear except beam FW_M2, which exhibited a bending failure. However, beam FW_M2 was considered in this section due to the limited number of specimens available, and its result could be regarded as a lower bound of the FRCM shear strength contribution. The carbon FRCM tensile strength, obtained by tensile testing of FRCM dumbbell shape specimens (Koutas and Bournas 2019), was σ_m = 1382 MPa, whereas the fiber elastic modulus was E_f = 225 GPa. Since no specific tests were carried out to investigate the FRCM bond behavior, the parameters considered in D’Antino et al. (2020) for a similar carbon FRCM composite were adopted. For the U-wrapped members, the FRCM experimental shear strength V_f,exp, obtained by subtracting the unstrengthened member shear strength from the strengthened member shear strength, was compared with the corresponding FRCM theoretical shear strength V_f,th obtained by Eq. (25). For fully-wrapped members, the FRCM analytical shear strength V_f,th was obtained by Eq. (17). The results obtained, depicted in Fig. 4, show that both Eq. (17) and (25) provided a reasonably accurate estimation of V_f,exp. However, further analysis should be carried out to verify the effect of corner radius (not included in the model due to the lack of experimental results), composite tensile strength, and crack opening angle with respect to the concrete shear strength contribution (i.e. α_u needs to be defined).

Fig. 4.

Comparison between theoretical and experimental results.

6 Conclusions

This paper analyzed the shear strength contribution of FRCM composites fully-wrapped to RC members. Employing the truss analogy and assuming that failure occurs due to the opening of a main diagonal shear crack, the FRCM shear strength contribution was modeled according to the corresponding composite-concrete bond behavior. An analytical model was proposed and validated by comparing the analytical and experimental results of RC beams strengthened in shear with a carbon FRCM composite found in the literature. The analysis and results obtained allowed for drawing the following conclusions:

• The analytical model proposed is able to describe the FRCM shear strength contribution accounting for the bond behavior of the specific FRCM and possible presence of friction.

• According to the analytical model, the fully-wrapped configuration may provide an FRCM shear strength contribution significantly higher than the U-wrapped configuration. However, the improvement depends on the member geometry, composite bond behavior and tensile strength, and crack opening angle.

• The analytical model showed accurate approximation for the experimental results considered. However, further analyses are needed to clarify the effect of the member cross-section corner radius, composite tensile strength, and crack opening angle.