Keywords

1 Introduction

Multi-criteria Decision-Analysis (MCDA) methods belong to the rapidly growing branch of operational research. They are widely used and developed by many scientists around the world. Their popularity is associated with the need to solve increasingly complex decision-making problems. One of the sources of this complexity is that MCDA methods increasingly have to use uncertain data. Sometimes it is also associated with problems in which partly incomplete data occur [10, 15].

The most straightforward approach to dealing with uncertain data is to use interval values instead of exact values. However, the solution to such a problem usually remains the numerical interval. To obtain a ranking from these values, one has to wonder what the preference interval represents. This is because it defines the smallest and largest possible assessment that an alternative can receive. Therefore, comparing the two alternatives, we can only periodically determine the exact ranking if they are separable intervals. Many methods also use other forms of expression of uncertain values such as fuzzy numbers [18], hesitant fuzzy numbers [2], interval valued fuzzy numbers [3], q-rung orthopair fuzzy set [11] or intuitionistic 2-tuple linguistic sets [4]. However, this work is limited to the ranking of the interval values.

This paper’s main contribution is a new approach to ranking a set of alternatives, where alternatives have been assessed in an interval form. The proposed method is based on the possibility degree of two intervals. In order to rank the alternatives, a matrix should be defined that contains all the possibility degrees. Our work compares seven different definitions of the possibility degree. The numerical example is presented to show the efficiency of the proposed method and comparing with naive approaches. For this purpose, we considered assessing ten electric vans, where the part of the data was presented as interval numbers. The Characteristic Object METhod (COMET) was used to obtain preference intervals. This method was used because it does not require the weight of criteria. Obtained results have been compared by using similarity coefficients.

The rest of the paper is organised as follows. The priority degree definitions are given in Sect. 2. The COMET method and similarity coefficients are presented in Sect. 3. In Sect. 4, we propose a new approach to rank alternatives in the decision-making domain. The numerical example is given in Sect. 5. In Sect. 6, we conclude the paper.

2 Preliminries

Let suppose that we have two intervals \(A=[a^L, a^R]\) and \(B=[b^L, b^R]\), where \(a_L<a_R\) and \(b_L<b_R\). Then according to [16], the possibility degree \(A\ge B\) is defined as \(P(A \ge B)\). In the literature, various mathematical definitions can be found (1–7) [1, 6,7,8]. For example, Wang et al. [17] presented a simple equation (1) which provides the degree of possibility that one interval is greater than another. Currently, this approach seems to be most popular in the literature.

$$\begin{aligned} \mathrm {P}_{1}(A \ge B)=\frac{\max \left( 0, a^{R}-b^{L}\right) -\max \left( a^{L}-b^{R}, 0\right) }{a^{R}+b^{R}-b^{L}-a^{L}} \end{aligned}$$
(1)

Equations (2–4) give the same results as method presented by Wang et al. [17], what was proved by Gao in [5]. The methods are presented on account of the different approach adopted in determining the formulas:

$$\begin{aligned} \mathrm {P}_{2}(A \ge B)=\frac{\max \left\{ 0, a^{R}-a^{L}+b^{R}-b^{L}-\max \left( b^{R}-a^{L}, 0\right) \right\} }{a^{R}+b^{R}-b^{L}-a^{L}} \end{aligned}$$
(2)
$$\begin{aligned} \mathrm {P}_{3}(A \ge B)=\left\{ \begin{aligned}&1, b^{R}<a^{L} \\&\frac{a^{R}-b^{L}}{a^{R}-a^{L}+b^{R}-b^{L}}, b^{L}<a^{R}, a^{L} <b^{R} \\&0, b^{L} > a^{R} \end{aligned}\right. \end{aligned}$$
(3)
$$\begin{aligned} \mathrm {P}_{4}(A \ge B)=\max \left\{ 1-\max \left( \frac{b^{R}-a^{L}}{a^{R}-a^{L}+b^{R}-b^{L}}, 0\right) , 0\right\} \end{aligned}$$
(4)

Other methods, although less frequently used, are also an important element of our study and are presented as follow (5)–(7):

$$\begin{aligned} \mathrm {P}_{5}(A \ge B)=\left\{ \begin{aligned}&1, b^{R}<a^{L} \\&\frac{\left( a^{R}-b^{L}\right) ^{2}}{\left( a^{R}-b^{L}\right) ^{2}+\left( b^{R}-a^{L}\right) ^{2}}, b^{L}<a^{R}, a^{L} <b^{R} \\&0, b^{L} \ge a^{R} \end{aligned}\right. \end{aligned}$$
(5)
$$\begin{aligned} \mathrm {P}_{6}(A \ge B)=\frac{1}{2}\left( 1+\frac{\left( a^{R}-b^{R}\right) +\left( a^{L}-b^{L}\right) }{\left| a^{R}-b^{R}\right| +\left| a^{L}-b^{L}\right| +l_{A B}}\right) , \end{aligned}$$
(6)

where \(l_{AB}\) means the length of the overlap part of two intervals and can be calculated as (8);

$$\begin{aligned} \mathrm {P}_{7}(A \ge B)=\left\{ \begin{aligned}&1, b^{R}<a^{L} \\&1-\frac{\left( b^{L}-a^{R}\right) ^{2}}{2 l_{A} l_{B}}, b^{L}<a^{L}<b^{R}<a^{R} \\&\frac{a^{L}+a^{R}-2 b^{L}}{2 l_{B}}, b^{L}<a^{L}<a^{R}<b^{R} \\&\frac{2 a^{R}-b^{L}-b^{R}}{2 l_{B}}, a^{L}<b^{L}<b^{R}<a^{R} \\&\frac{\left( a^{R}-b^{L}\right) ^{2}}{2 l_{A} l_{B}}, a^{L}<b^{L}<a^{R}<b^{R} \\&0, a^{R}<b^{L} \end{aligned}\right. \end{aligned}$$
(7)

where \(l_{A}\) and \(l_{B}\) are the lengths of interval A and B respectively.

$$\begin{aligned} l_{A B}=\left\{ \begin{array}{c} 0, \quad b^{L}>a^{R} \vee a^{L}>b^{R} \\ \min \left( a^{R}, b^{R}\right) -\max \left( a^{L}, b^{L}\right) , \textit{otherwise} \end{array}\right. \end{aligned}$$
(8)

3 Methods

3.1 The COMET Method

The COMET is a newly developed method for identifying a multi-criteria expert decision-making model to solve complex problems. This method is used in the numerical example to obtained interval preferences. The whole algorithm can be presented as five following steps and has been provided following [12].

Step 1. Define the space of the problem—an expert determines dimensionality of the problem by selecting number r of criteria, \(C_1, C_2, ..., C_r\). Subsequently, the set of fuzzy numbers for each criterion \(C_i\) is selected, i.e., \(\tilde{C}_{i1}, \tilde{C}_{i2}, ..., \tilde{C}_{ic_i}\). Each fuzzy number determines the value of the membership for a particular linguistic concept for specific crisp values. Therefore it is also useful for variables that are not continuous. In this way, the following result is obtained (9).

$$\begin{aligned} \begin{array}{l} C_1 = \{\tilde{C}_{11}, \tilde{C}_{12}, ..., \tilde{C}_{1c_1}\} \\ C_2 = \{\tilde{C}_{21}, \tilde{C}_{22}, ..., \tilde{C}_{2c_1}\} \\ ... ... ... ... ... ... ... ... ... ... ... \\ C_r = \{\tilde{C}_{r1}, \tilde{C}_{r2}, ..., \tilde{C}_{rc_r}\} \end{array} \end{aligned}$$
(9)

where \(c_1,c_2,...,c_r\) are numbers of the fuzzy numbers for all criteria.

Step 2. Generate the characteristic objects—characteristic objects are objects that define reference points in n-dimensional space. They can be either real or idealized objects that cannot exist. The characteristic objects (CO) are obtained by using the Cartesian product of fuzzy numbers cores for each criteria as follows (10):

$$\begin{aligned} CO = \{ \{C(\tilde{C}_{11}), C(\tilde{C}_{12}), ..., C(\tilde{C}_{1c_1})\} \times ... \times \{C(\tilde{C}_{r1}), C(\tilde{C}_{r2}), ..., C(\tilde{C}_{rc_r})\}\} \end{aligned}$$
(10)

As the result, the ordered set of all CO is obtained (11):

$$\begin{aligned} \begin{array}{l} CO_1 = \{C(\tilde{C}_{11}), C(\tilde{C}_{21}), ..., C(\tilde{C}_{r1})\} \\ CO_2 = \{C(\tilde{C}_{11}), C(\tilde{C}_{21}), ..., C(\tilde{C}_{r2})\} \\ ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...\\ CO_t = \{C(\tilde{C}_{1{c_1}}), C(\tilde{C}_{2{c_2}}), ..., C(\tilde{C}_{rc_r})\} \end{array} \end{aligned}$$
(11)

where t is a number of CO (12):

$$\begin{aligned} t=\prod ^{r}_{i=1}c_i \end{aligned}$$
(12)

Step 3. Rank the characteristic objects—the expert determines the Matrix of Expert Judgement (MEJ). It is a result of pairwise comparison of the characteristic objects by the expert knowledge. The MEJ structure is as follows (13):

$$\begin{aligned} MEJ= \left( \begin{array}{cccc} \alpha _{11} &{} \alpha _{12} &{} ... &{} \alpha _{1t}\\ \alpha _{21} &{} \alpha _{22} &{} ... &{} \alpha _{2t}\\ ... &{} ... &{} ... &{} ...\\ \alpha _{t1} &{} \alpha _{t2} &{} ... &{} \alpha _{tt} \end{array} \right) \end{aligned}$$
(13)

where \(\alpha _{ij}\) is a result of comparing \(CO_i\) and \(CO_j\) by the expert. The more preferred characteristic object gets one point and the second object get zero points. If the preferences are balanced, the both objects get half point. It depends solely on the knowledge of the expert and can be presented as (14):

$$\begin{aligned} \alpha _{ij} = \left\{ \begin{array}{ll} 0.0 , &{} f_{exp}(CO_i)<f_{exp}(CO_j)\\ 0.5 , &{} f_{exp}(CO_i)=f_{exp}(CO_j)\\ 1.0 , &{} f_{exp}(CO_i)>f_{exp}(CO_j) \end{array} \right. \end{aligned}$$
(14)

where \(f_{exp}\) is an expert mental judgement function. Afterwards, the vertical vector of the Summed Judgements (SJ) is obtained as follows (15):

$$\begin{aligned} SJ_i=\sum ^{t}_{j=1}\alpha _{ij} \end{aligned}$$
(15)

The number of query is equal \(p = \frac{t(t-1)}{2}\) because for each element \(\alpha _{ij}\) we can observe that \(\alpha _{ji}=1-\alpha _{ij}\). The last step assigns to each characteristic object an approximate value of preference \(P_i\) by using the following Matlab pseudo-code:

figure a

In the result, the vector P is obtained, where i-th row contains the approximate value of preference for \(CO_i\).

Step 4. The rule base—each characteristic object is converted into a fuzzy rule, where the degree of belonging to particular criteria is a premise for activating conclusions in the form of \(P_i\). Each characteristic object and value of preference is converted to a fuzzy rule as follows detailed form (16). In this way, the complete fuzzy rule base is obtained, that approximates the expert mental judgement function \(f_{exp}(CO_i)\).

(16)

Step 5. Inference and final ranking—The each one alternative \(A_i\) is a set of crisp numbers \(a_{ri}\) corresponding to criteria \(C_1, C_2, ..., C_r\). It can be presented as follows (17):

$$\begin{aligned} A_i=\{ a_{1i}, a_{2i}, ..., a_{ri} \} \end{aligned}$$
(17)

Each alternative activates the specified number of fuzzy rules, where for each one is determined the fulfilment degree of the complex conjunctive premise. Fulfilment degrees of all activated rules are summed to one. The preference of alternative is computed as the sum of the product of all activated rules, as their fulfilment degrees, and their values of the preference. The final ranking of alternatives is obtained by sorting the preference of alternatives, where one is the best result, and zero is the worst. More details can be found in [9].

3.2 Similarity Coefficients

For a samples of size N, the rank values \(x_i\) and \(y_i\) is defined as (18) for WS coefficient [13] and as (19) for weighted Spearman’s rank correlation coefficient. For the WS coefficient, the given comparison value is determined by the relevance of the position relative to the first ranking. This ranking is referential, and the coefficient itself determines the similarity of the second-ranking to referential. Therefore, it is an asymmetric measure.

$$\begin{aligned} WS = 1 - \sum _{i=1}^{N} 2^{-x_i} \frac{|x_i - y_i|}{max(|x_i - 1|, |x_i - N|)} \end{aligned}$$
(18)

In the second approach, the positions at the top of both rankings are more important than the rest positions. The weight of significance is calculated for each comparison. It is the element that determines the main difference to the Spearman’s rank correlation coefficient, which examines whether the differences appeared and not where they appeared [14].

$$\begin{aligned} r_w = 1 - \frac{6 \sum _{i=1}^{N} (x_i - y_i)^2 ((N - x_i + 1) + (N - y_i + 1))}{N^4 + N^3 - N^2 - N} \end{aligned}$$
(19)

4 The Proposed Approach

Let us assume that we have N alternatives that have been assessed using the appropriate MCDA method. A suitable MCDA method must be applicable, correctly selected according to [19] and returns the preference results in the form of intervals. In the following, the universal COMET method described in Sect. 3.1 will be used.

As a result of the evaluation, we obtained preference intervals for all alternatives, which can be written as \(A_i =[A^L_i, A^R_i]\), where \(i = 1...N\). Then, the Possibility Degree (PD) matrix with all values of the possibility degree should be determined as follow (20):

$$\begin{aligned} PD=[P(A_i \ge A_j)]_{N \times N} \end{aligned}$$
(20)

where \(i = 1...N\), \(j = 1...N\), and P is used one of the equation (1)–(7). Then we count the cumulative probability vector PR in according to (21):

$$\begin{aligned} PR_i=\sum ^{N}_{j=1}PD_{ij} \end{aligned}$$
(21)

Finally, the alternatives are ranked from the highest to the smallest value of \(PR_i\), where the highest value means the maximum cumulative probability degree. This approach will be compared in the next section with three naive approaches, i.e., ranking made up of \(A^L_i\) pessimistic version, \(A^R_i\) optimistic version and \(\frac{A^L_i + A^R_i}{2}\) average version.

5 Comparative Study Case

This study case is based on data and initial results published in [20]. The decision problem is about obtaining a ranking of electronic vans according to selected nine criteria. We randomly selected ten electric vans, which we use to demonstrate the effectiveness of our approach. The description of all criteria is presented in Table 1.

Table 1. Description of the criteria.
Full size table

Table 2 shows all the vans selected at random and their performance concerning the analysed criteria. Some attributes are given as exact numerical values and some as intervals. This is due to the partial lack of data on engine torque, battery charging time 80%, battery capacity, and price.

Table 2. The performance table of the alternatives \(A_1-A_{10}\) in respect to nine criteria.
Full size table

In order to present our ranking approach, a first assessment should be made using the COMET method. Table 3 gives each criterion’s characteristic values that will be used to calculate the intervals of preference for each alternative.

Table 3. Characteristic values for each criterion.
Full size table

The detailed results of the COMET interval assessments and the reference ranking derived from [20] are presented in Table 4. It should be borne in mind that this task is solved under uncertain conditions, which means that an exact solution cannot be expected in the sense of specific data. Some discrepancies are observed due to the burden of uncertain data.

Table 4. Interval preferences P and reference ranking.
Full size table

Based on the results obtained in column P of Table 4, the approach proposed in Sect. 4 is applied to calculate vector PR, which contain the cumulative possibility degree for each alternative. Table 5 presents detailed results for the different methods of determining the probability degree, according to (1)–(7) and naive approaches. As formulas (1)–(4) give the same results, only formula (1) is included in the table. In each analysed case, higher values mean a higher position in the ranking. The complete ranking for each approach is presented in Table 6. Most of the methods correctly indicated the first position of the ranking. However, none of the approaches accurately represent the reference ranking, what was easy to predict. All approaches have indicated \(A_9\) as the worst alternative, ranked sixth in the reference ranking.

Table 5. The cumulative possibility degree and results by using naive approaches.
Full size table
Table 6. Rankings based on the cumulative possibility degree and naive approaches.
Full size table
Fig. 1.
figure 1

Thermal maps of \(r_w\) and WS correlations

Full size image

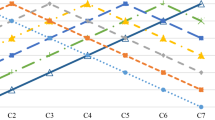
Comparing individual places in the received rankings makes it quite challenging to indicate which ranking fits the reference better. Of course, only the ranking based on the formula 7 correctly indicated the second position in the ranking. However, to comprehensively compare the obtained rankings, similarity coefficients of rankings \(r_w\) and WS described in Sect. 3.2 were calculated. Figure 1 shows thermal maps of both indicators calculated for all rankings. Analysing Fig. 1 we will focus on the first line. For the \(r_w\) coefficient, it is clear that the worst match is achieved by choosing a pessimistic solution (min column). Only for this ranking, a negative correlation was obtained. The other rankings are quite similar to the reference ranking, and the value of the index oscillates around 0.80. The best match has been suggested using the possibility degree according to the formula (7).

The situation is similar when we take the WS coefficient into account. However, we see a much better fit for the proposed approach using the formula 7. The resulting value of 0.97 indicates a very high similarity of this ranking to the reference ranking. These coefficients are mainly focused on the top of the ranking and not on its final part. As shown in the example shown, the proposed approach can effectively rank a set of alternatives assessed using interval values.

6 Conclusions

This paper proposes a new approach to the ranking of alternatives assessed by interval values. The proposed approach is based on the possibility degree. In this work, we have prepared seven possible formulas that can be used to calculate the cumulative possibility degree matrix. The numerical example demonstrated that, for the designated rankings, the proposed approach had returned rankings largely in line with the reference ranking. The proposed approach gave a better result on average than the three presented naive methods. More extensive tests should be carried out in future research directions to improve setting rankings based on interval values, and the proposed approach should be extended to include fuzzy numbers.