Keywords

1 Introduction

Quantum image processing focuses on the use of quantum computing [1] and quantum information processing to create and work with quantum images. Due to some of the amazing properties inherent in quantum computing, notably entanglement and parallelism, quantum information processing technologies are expected to offer capabilities and characteristics that are unmatched in their traditional equivalents. These improvements can be associated with computational speed, guaranteed security, minimal storage requirements, etc. However, modern image processing methods require expensive computational resources, storage and image processing. There are many computational techniques, such as Fast Fourier Transform (FFT), which provide acceleration for image processing. Quantum computing, on the other hand, defines a probabilistic approach for representing classical information using methods from quantum theory. The idea of quantum information was first introduced in 1980 by Paul Benioff. In the same year, Yuri Manin proposed a model of a quantum computer in his book “Computable and Uncomputable”. In 1982, the field of quantum information theory was formalized and described by Richard Feynman, who made it popular with his paper on modeling physics in computers. Devid Deutsch took this field forward with the development of the quantum Turing machine. Thanks to these advances, quantum computing [2] has shown many promises for the future of computers. This new class of problem computability has been grouped into a computational class called bounded error quantum polynomial time (BEQP).

The basic idea behind quantum computing is the qubit [3], the quantum analogue of the classical computer bit. A classic bit is only capable of storing a specific value (0 or 1). A qubit can store both 0 and 1 in an undefined state called a superposition:

$${\upalpha } |0 > + {\upbeta } |1 >, $$
(1)

where α and β are normalized probability amplitudes.

Formulation of the problem. The aim of the study is to build a modular specialized system for new information technologies and algorithms, analyze their performance and computational complexity. Realization of the theoretical foundations for the creation of software systems for new information technologies of a quantum orientation. It also consists in the development of theoretical, algorithmic and practical foundations for building a modular system for the interaction of information processes and algorithms with an open architecture.

2 Mathematical Apparatus

The logic and mathematical apparatus of quantum computing devices differs significantly from the logic and mathematics of classical computing technology due to the nature and specific properties of quantum particles (qubits), which allow such calculations to be carried out. The quantum computer operates, as described above, with quantum bits, which have two basic states \(\left| 0 \right\rangle = { }\left( {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right)\) and \(\left| 1 \right\rangle = \left( {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right)\). The qubit state |0⟩ corresponds to the spin up state of an electron in the atom [4], the spin down state corresponds to |1⟩, and the mixed state (superposition of states) corresponds to the intermediate spin position. Spin is the proper angular momentum of elementary particles, but the spin is not associated with motion in space, it is the eigenvalue of a quantum particle, which cannot be explained from the standpoint of classical mechanics. In the general case, the state of a qubit is described by a wave function (or a state vector):

$$ \left| {\uppsi } \right\rangle = {\upalpha }_{0} \left| 0 \right\rangle + {\upalpha }_{1} \left| 1 \right\rangle $$
(2)

where \({\upalpha }_{0} , {\upalpha }_{1} \in {\text{C}}\), \({\upalpha }_{0}\) and \({\upalpha }_{1}\) are the complex amplitudes of the reading probability |0⟩ or |1⟩. The fact is that when measuring quantum bits in a standard basis with the probability \(\left| {{\upalpha }_{0} } \right|^{2}\), |0⟩ will be obtained, and with the probability \(\left| {{\upalpha }_{1} } \right|^{2}\) – \(\left| 1 \right\rangle\). In this case, the qubit will go into a state of quantum zero or one. The effect of a quantum mixed state exists only until the moment the qubit is measured, that is, when reading, we bring the qubit into one of the basic states, and which one depends on the probability obtained in the calculations. Another visual option for representing the qubit state vector is the so-called Bloch sphere [5]. It is a mapping of the complex plane of psi-function values onto a sphere, in fact, on it you can visually see “spin up”, “spin down”. However, this is the space of values of the qubit state, while the spin pseudovector itself cannot be negative. Analyzing Fig. 1, one can notice that the multiplication of the state of the qubit |ψ⟩ by eiφ does not change the probability of reading zero and one.

Fig. 1.
figure 1

Bloch sphere.

Full size image

The state of a system of two quantum bits is described with respect to four basic states (in a classical computer, four states can be encoded with two bits): |00⟩, |01⟩, |10⟩, |1⟩.

$$ \left| {\uppsi } \right\rangle = {\upalpha }_{0} \left| {00} \right\rangle + {\upalpha }_{1} \left| {01} \right\rangle + {\upalpha }_{2} \left| {10} \right\rangle + {\upalpha }_{3} \left| {11} \right\rangle , $$
(3)
$$ \left| {{\upalpha }_{0} } \right|^{2} + \left| {{\upalpha }_{1} } \right|^{2} + \left| {{\upalpha }_{2} } \right|^{2} + \left| {{\upalpha }_{3} } \right|^{2} = 1 $$
(4)

That is, the multi-qubit system in formula (4) describes all possible states (combinations of zeros and ones), the number of combinations is found by the formula:

$$ N = 2^{q} $$
(5)

where N is the number of basis states that a given quantum system of qubits describes, and q is the number of qubits in the system. At the beginning of the analysis, it was indicated that the states of zero and one are encoded as \(\left| 0 \right\rangle = { }\left( {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right){ }\) and \(\left| 1 \right\rangle = \left( {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right)\) state function \(\left| {\uppsi } \right\rangle = {\upalpha }_{0} \left| 0 \right\rangle + {\upalpha }_{1} \left| 1 \right\rangle\), but if we expand the product \({\upalpha }_{0} \left| 0 \right\rangle\), then we get the following:

$$ {\upalpha }_{0} \left| 0 \right\rangle = {\upalpha }_{0} \left( {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {{\upalpha }_{0} } \\ 0 \\ \end{array} } \right) $$
(6)

those, the first line contains the amplitude of the probability of reading zero. And for \({\upalpha }_{1} \left| 1 \right\rangle\) we get that the second line contains the amplitude of the probability of reading one:

$$ {\upalpha }_{1} \left| 1 \right\rangle = {\upalpha }_{1} \left( {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} 0 \\ {{\upalpha }_{1} } \\ \end{array} } \right). $$
(7)

Then it becomes clear how the function \(\left| {\uppsi } \right\rangle = {\upalpha }_{0} \left| 0 \right\rangle + {\upalpha }_{1} \left| 1 \right\rangle\) contains the probabilities of all states:

$$ \left| {\uppsi } \right\rangle = {\upalpha }_{0} \left| 0 \right\rangle + {\upalpha }_{1} \left| 1 \right\rangle = \left( {\begin{array}{*{20}c} {{\upalpha }_{0} } \\ 0 \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} 0 \\ {{\upalpha }_{1} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {{\upalpha }_{0} } \\ {{\upalpha }_{1} } \\ \end{array} } \right). $$
(8)

The first line contains the amplitude of the probability to get 0 when reading, and the second to get the probability when reading 1. If we consider a system consisting of two qubits, then its state vector is described as follows:

$$ \begin{gathered} \left| {\uppsi } \right\rangle = {\upalpha }_{0} \left| {00} \right\rangle + {\upalpha }_{1} \left| {01} \right\rangle + {\upalpha }_{2} \left| {10} \right\rangle + {\upalpha }_{3} \left| {11} \right\rangle \hfill \\ = {\upalpha }_{0} \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \right) + {\upalpha }_{1} \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \right) + {\upalpha }_{2} \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 1 \\ 0 \\ \end{array} } \\ \end{array} } \right) + {\upalpha }_{3} \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ 1 \\ \end{array} } \\ \end{array} } \right) \hfill \\ = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\upalpha }_{0} } \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {{\upalpha }_{1} } \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} {{\upalpha }_{2} } \\ 0 \\ \end{array} } \\ \end{array} } \right) + \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ 0 \\ \end{array} } \\ {\begin{array}{*{20}c} 0 \\ {{\upalpha }_{3} } \\ \end{array} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\begin{array}{*{20}c} {{\upalpha }_{0} } \\ {{\upalpha }_{1} } \\ \end{array} } \\ {\begin{array}{*{20}c} {{\upalpha }_{2} } \\ {{\upalpha }_{3} } \\ \end{array} } \\ \end{array} } \right) \hfill \\ \end{gathered} $$
(9)

3 Quantum Image Processing Theory

Consider the case of using quantum information by encoding 8 bits of binary information into 3 qubits. The key feature of a qubit is the ability to store an undefined value as a superposition [6] of “0” and “1”. Therefore, any operation will inherently receive 0 or 1, as shown in Table 1.

Table 1. Possible states of a 3-qubit register.
Full size table

A three-bit quantum register (Ψ = ψ1ψ2ψ3) can store 8 bits of information in superposition, where each configuration is assigned a probability amplitude as shown below:

$$ {\upvarphi} = {\upalpha }_{0} |000 > + {\upalpha }_{1} |001 > + \ldots + {\upalpha }_{{2^{{\text{n}}} - 1}} |111 $$
(10)

The probability amplitudes (\({\upalpha }_{1}\), \({\upalpha }_{2} ,{ }\)…) represent the probability that the quantum register will be in this configuration. It is also very important to note that quantum logic gates [7] have some unique advantages that classical systems cannot take advantage of. For example, the 2-qubit CNOT gate is reversible. This means that if this gate is applied twice, the qubit will return to its original state. To represent quantum images, you can use this gate to build a circuit for preparing a quantum image. The CNOT gate can be used as a conditional switch, since it only flips the target bit if the input is 1. It is also possible to attach any other unitary operation to the conditional gate instead of the NOT gate to implement the conditional operation. Technically innovative efforts in the field of quantum pattern and object recognition, with subsequent research related to them, can be divided into three main groups:

  • Quantum image processing. These applications are aimed at improving the tasks and applications of digital or classical image processing.

  • Optical quantum visualization;

  • Quantum image processing based on classical methods.

A review of the quantum representation of an image was published in [8]. In addition, the recently published book Quantum Image Processing [9] provides a comprehensive introduction to quantum image processing, which focuses on extending traditional image processing problems to quantum computing platforms [10]. It briefly presents the available representations of quantum images and their operations, discusses possible applications of quantum images and their implementation, and discusses open questions and future development trends.

3.1 Quantum Image Manipulation

Much of the effort has been focused on developing algorithms [11] for manipulating position and color information encoded using a quantum image representation and its many variations. For example, fast geometric transformations were initially proposed, including (two-point) swap, flip, orthogonal rotations, and constrained geometric transformations, to constrain these operations to a specific area of the image. Recently, a rather interesting idea of quantum images was implemented based on a new extended quantum representation to match the position of each image element in the input image with a new position in the output image and upscale the quantum image to resize the quantum image. While based on the representation of a quantum image, the general form of color transforms was first proposed using single-bit gates such as gates X, Z and H.

Using basic quantum elements and the aforementioned operations, researchers have contributed to the extraction of quantum characteristics of an image, quantum image segmentation, quantum image morphology, quantum image comparison, quantum image filtering, quantum image classification, quantum image stabilization.

3.2 Quantum Image Transformation

By coding and processing image information in quantum mechanical systems [12], the basis of quantum image processing is presented, where a pure quantum state encodes image information: to encode pixel values in probability amplitudes and pixel positions in basic computational states. Given an image \({\text{F}} = \left( {{\text{F}}_{{{\text{i}},{\text{j}}}} } \right)_{{\text{M*L}}}\), where \({\text{F}}_{{{\text{i}},{\text{j}}}}\) represents the pixel value at position (i, j) with i = 1,…, M and j = 1,…, L, a vector f with ML elements can be formed by placing the first elements of M in the vector f will be the first column of F, the next M elements will be the second column, and so on.

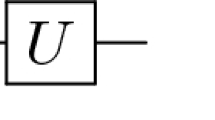
A large class of image operations are linear, such as unitary transformations, convolutions, and linear filtering. In quantum computing, a linear transformation can be represented as |g >  = U |f > with the input image state |f > and the output image state |g >. A unitary transformation can be implemented as a unitary evolution. Some basic and commonly used image transformations (for example, the Fourier, Hadamard and Haar wavelet transforms) can be expressed as G = PFQ with the resulting image G and the row (column) transformation matrix P (Q). The corresponding unitary operator U can be written as \({\text{U}} = {\text{Q}}^{{\text{T}}} \cdot {\text{P}}\). Several commonly used 2D image transformations such as Haar wavelet, Fourier transform and Hadamard transform have been experimentally demonstrated on a quantum computer with exponential acceleration compared to their classical counterparts. In addition, a new highly efficient quantum algorithm has been proposed and experimentally implemented for detecting the boundary between different regions of the image: it requires only one one-bit gate at the processing stage, regardless of the image size.

4 Implementing a Quantum Computing Simulation Environment

In Fig. 2 shows the developed model of a quantum computing device and the result of executing the quantum algorithm for transforming a set of pixels. This software development is an offline desktop computing system with an open architecture, but in the future, it is planned to be broadcast online.

Fig. 2.
figure 2

Model of a quantum computing device.

Full size image

The measurement process consists in playing a random number from the interval [0,1]. When the value falls into the interval [0,|c1|2], the output value of the measuring process is the basic state of the bra of vector 0, otherwise (interval [|c1|2,1]) - the quantum state of the bra of vector 1.

In the latest quantum computer technology, only a limited number of qubits can be well controlled and controlled. Whereas, on the other hand, the real problem of optical recognition of symbols in the quantum support vector method requires tens of qubits, which cannot be implemented at present. Thus, we will restrict the problem to the case with minimal costs, in which only two options (“6” or “9”) are in the list and only two properties (horizontal or vertical position, determined later) constitute the problem. This makes it possible to demonstrate this quantum artificial intelligence algorithm based on the 4-qubit moment of a quantum processor core at room temperature. The developed algorithm uses quantum principles, such as superposition of quantum states of a computing system, entanglement of quantum states, and transformation of a classical image into a quantum state by encoding the color palette of a pixel set within complex amplitude quantum states.

5 Comparison of Image Transformation Models and Their Classification

Technically, these pioneering efforts, with the subsequent research associated with them, can be divided into three main groups, of which (1) and (2) are considered outside the scope of this review:

  1. (1)

    Quantum digital image processing: these applications are designed to take advantage of some of the properties responsible for the efficiency of quantum computing algorithms to improve some well-known digital or classical image processing problems and applications

  2. (2)

    Optics-based quantum imaging: These applications focus on the development of new methods of optical imaging and parallel processing of information at the quantum level by exploiting the quantum nature of light and the intrinsic parallelism of optical signals.

  3. (3)

    Classical style QIP: These applications take inspiration from the expectation that quantum computing hardware will soon be physically realized and hence such research aims to expand classical imaging problems and applications to the quantum computing framework.

Venegaz-Andraza and Bose introduced the representation of images on quantum computers by proposing a lattice of qubits method where each pixel was represented in its quantum state and then a quantum matrix was created with them. However, this is just a quantum analogue of the classical image and there is no additional advantage in quantum form. However, the next huge advance is the creation of a flexible quantum imaging model (FQI) for multiple intensity levels. The GPKI representation is expressed mathematically as follows:

$$ |{\text{I}}\left( {\uptheta } \right) > = \frac{1}{{2^{{\text{n}}} }}\sum\nolimits_{{{\text{i}} = 0}}^{{2^{{2{\text{n}}}} - 1}} {\left( {{\text{sin}}\left( {{\uptheta }_{{\text{i}}} } \right)|0 > + {\text{cos}}\left( {{\uptheta }_{{\text{i}}} } \right)|1 > } \right)|{\text{i > }}} $$
(11)

where θ corresponds to the intensity of the i-th pixel. Since the intensity values are encoded in the amplitudes of the quantum state, it is relatively easy to apply various transforms, such as the quantum Fourier transform, since they are applied directly to the amplitude of the image. Another approach describes the representation of the pixel values of the image at baseline states instead of amplitudes as shown below:

$$ |{\text{I > }} = \frac{1}{{2^{{\text{n}}} }}\sum\nolimits_{{{\text{X}} = 0}}^{{2^{{2{\text{n}}}} - 1}} {\sum\nolimits_{{{\text{Y}} = 0}}^{{2^{{2{\text{n}}}} - 1}} {\left| {{\text{f}}\left( {{\text{X}},{\text{Y}}} \right)} \right\rangle |{\text{XY}} > } } $$
(12)

where f (X, Y) refers to the intensity of the pixels in (X, Y). These methods are pretty comprehensive, but they have their own drawbacks. The first major drawback is that they require a square image (\(2^{{\text{N}}} {*}2^{{\text{N}}}\)) along with the need for qubits to encode positions along with pixel intensities. Comparison of the existing and the proposed quantum model of images can be seen in Table 2.

Table 2. Comparison of quantum imaging models.
Full size table

Most quantum imaging models can be prepared with Hadamard gates and controlled operator flip. For \(2^{{\text{N}}} {*}2^{{\text{N}}}\), the first step is to initialize n qubits when \(|0 >^{{ \otimes 2{\text{n }} + { }1}}\). We then apply a Hadamard gate to each qubit to place them in superposition.

$$ {\text{H}}\left( {|0 >^{{ \otimes 2{\text{n }} + { }1}} } \right) = \frac{1}{{2^{{\text{n}}} }}|0 > \otimes \sum\nolimits_{{{\text{i}} = 0}}^{{2^{{2{\text{n}}}} - 1}} {|{\text{i > }}} $$
(13)

Next, we apply the guided rotation operators to each base state resulting in a shared state:

$$ {\text{R}}\left| {{\text{H}} > = \left( {\prod\nolimits_{{{\text{i}} = 0}}^{{2^{{2{\text{n}}}} - 1}} {{\text{R}}_{{\text{i}}} } } \right)} \right|{\text{H}} \ge |{\text{I}}\left( {\uptheta } \right) > $$
(14)

Each of the \({\text{R}}_{{\text{i}}} { }\) rotations correspond to a specific pixel rotation. Therefore, we encode the intensities by rotating these quantum states. The implementation scheme can be achieved by combining Hadamard, CNOT and phase shifting gates. We will introduce FPQI because of its simple and efficient function, which allows us to preserve the intensity of the image as the amplitude of the probability of a quantum state. Gates of the same type are also used in the quantum Fourier transform scheme. We implement FPQI both on a classical computer and on an IBM quantum simulator (Fig. 3).

Fig. 3.
figure 3

Quantum Fourier transform scheme.

Full size image

Modeling quantum systems in a classical computer is computationally expensive. This is because we need to explicitly define the superposition (in other words, store the superposition in memory). In a real quantum computer, superposition is the property of the system and therefore does not need to be stored. For example, consider encoding N bits of information into \({\text{log}}_{2} {\text{N}}\) bits, a superposition of all possible combinations of 0 and 1 can be stored in a quantum register as opposed to a quantum register in which we can only store one of all possible states. A classical computer would have to store all possible states as a list (taking up extra space), unlike a quantum computer. This also means that we do not access these quantum bits as in the classical system. The n bits of information in these n qubits can be accessed only through measurement. The state we want to achieve is shown in Eq. 3. To build the circuit, use a 2 × 2 image as shown below:

$$ \left[ {\begin{array}{*{20}c} {{\uptheta }_{1} } & {{\uptheta }_{2} } \\ {{\uptheta }_{3} } & {{\uptheta }_{4} } \\ \end{array} } \right] $$
(15)

Such coding is possible by using a controlled rotation gate to rotate individual base states based on intensity. Let’s test this algorithm on a 2 × 2 image. The IBM simulator allows a small number of qubits to store an image larger than 2 × 2. Hence, we present the mechanics of a circuit encoding a 2 × 2 image in an IBM quantum register. We will use the server side of the simulator for the IBM Q 5 Tenerife. Let’s use a simple 2 × 2 image:

$$ I = \left[ {\begin{array}{*{20}c} 5 & 1 \\ 2 & 3 \\ \end{array} } \right] $$
(16)

Note that these intensities will be normalized. Therefore, we will not be able to accurately reconstruct the image. The image probability distribution is shown in Fig. 4 (Table 3).

Fig. 4.
figure 4

The resulting image as a probability distribution.

Full size image
Table 3. Open
Full size table

Since manipulation of intensities simply means controlled rotation, we can use the circuit in Fig. 1 to define specific gates. For example, negating an image would simply mean rotating the amplitude by π. Operations on a quantum image can be done by rotating quantum bits around a Bloch sphere. For example, to invert a quantum image, we can simply rotate the cube-bits around the Bloch sphere 180° and get Fig. 5.

Fig. 5.
figure 5

The resulting inverted image.

Full size image

6 Conclusions

Quantum image processing relies on the application of quantum computing and quantum information processing to create and manipulate quantum images. The field of quantum recognition of patterns and objects with subsequent research related to them can be divided into three main groups:

  • Quantum image processing;

  • Optical quantum visualization;

  • Quantum image processing based on classical methods.

The article considers the theory of quantum image processing and quantum image manipulation (fast geometric transformations, including (two-point) swap, flip, orthogonal rotations and limited geometric transformations). In this work, the study of the field of quantum image processing was carried out and the FPQI model was tested. Models (developed in the work, etc.) were investigated by explicitly modeling quantum behavior on a large quantum system. A basic scheme for encoding 2 × 2 images has been created to get a clearer understanding of the mechanics of quantum image models.