Topological Learning and Its Application to Multimodal Brain Network Integration

Abstract

A long-standing challenge in multimodal brain network analyses is to integrate topologically different brain networks obtained from diffusion and functional MRI in a coherent statistical framework. Existing multimodal frameworks will inevitably destroy the topological difference of the networks. In this paper, we propose a novel topological learning framework that integrates networks of different topology through persistent homology. Such challenging task is made possible through the introduction of a new topological loss that bypasses intrinsic computational bottlenecks and thus enables us to perform various topological computations and optimizations with ease. We validate the topological loss in extensive statistical simulations with ground truth to assess its effectiveness of discriminating networks. Among many possible applications, we demonstrate the versatility of topological loss in the twin imaging study where we determine the extend to which brain networks are genetically heritable.

1 Introduction

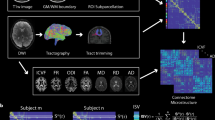
In standard brain network modeling, the whole brain is usually parcellated into a few hundred disjoint regions [7, 17, 27]. For instance, well established, widely used Automated Anatomical Labeling (AAL) parcellates the brain into 116 regions [27]. These disjoint regions form nodes in a brain network. Subsequently, functional or structural information is overlaid on top of the parcellation to obtain brain connectivity between the regions. Structural connectivity is obtained from diffusion MRI (dMRI), which traces the white matter fibers in the brain. Strength of the structural connectivity is determined by the number of fibers connecting the parcellations. Resting-state functional connectivity obtained from functional MRI (fMRI) is often computed using the Pearson correlation coefficient between average fMRI time series in the parcellations [7]. While the structural connectivity provides information whether the brain regions are physically connected through the white matter fibers, the functional connectivity can exhibit relations between two regions without a direct neuroanatomical connection [14]. Thus, functional brain networks are often very dense with thousands of loops or cycles [7] while structural brain networks are expected to exhibit sparse topology without many cycles. Both the structural and functional brain networks provide topologically different information (Fig. 1). Nonetheless, not much research has been done thus far on integrating the brain networks at the localized connection level. Existing integration frameworks will inevitably destroy the topological difference in the process [16, 30]. There is a need for a new multimodal brain network model that can integrate networks of different topology in a coherent statistical framework.

Fig. 1.

Schematic of topological learning. (a) AAL partitions the human brain into 116 disjoint regions. (b, c) Functional network G is obtained from resting-state fMRI. The template structural network P is obtained from dMRI. The structural network P is sparse while the functional network G is densely connected with many cycles. (d) We learn network $\varTheta$ that has the topological characteristics of both functional and structural networks.

Persistent homology [7, 9, 15, 17, 25] provides a novel approach to the long-standing challenge in multimodal brain network analyses. In persistent homology, topological features such as connected components and cycles are measured across different spatial resolutions represented in the form of barcodes. It was recently proposed to penalize the barcodes as a loss function in image segmentation [15]. Though the method allows to incorporate topological information into the problem, it is limited to an image with a handful of topological features due to its expensive optimization process with $O(n^3)$. This is impractical in brain networks with a far larger number of topological features comprising hundreds of connected components and thousands of cycles. In this paper, we propose a more principled and scalable topological loss with $O(n \log n)$. Our proposed method bypasses the intrinsic computational bottleneck and thus enables us to perform various topological computations and optimizations with ease.

Twin studies on brain imaging phenotypes provide a well established way to examine the extent to which brain networks are influenced by genetic factors. However, previous twin imaging studies have not been well adapted beyond determining heritability of a few brain regions of interest [2, 4, 12, 21, 24]. Measures of network topology are worth investigating as intermediate phenotypes that indicate the genetic risk for various neuropsychiatric disorders [3]. Determining heritability of the whole brain network is the first necessary prerequisite for identifying network based endophenotypes. With our topological loss, we propose a novel topological learning framework where we determine heritability of the functional brain networks while integrating the structural brain network information (Fig. 1). Our method increases statistical sensitivity to subtle topological differences, yielding more connections as genetic signals.

Fig. 2.

(a) Graph filtration of G. $\beta _0$ is monotonically increasing while $\beta _1$ is monotonically decreasing over the graph filtration. Connected components are born at edge weights $w_3,w_5,w_6$ while cycles die at edge weights $w_1,w_2,w_4$. 0D barcode is represented by a set of birth values $B(G)=\{w_3,w_5,w_6\}$. 1D barcode is represented by a set of death values $D(G)=\{w_1,w_2,w_4\}$. (b) The weight set $W=\{w_1,...,w_6\}$ is partitioned into 0D birth values and 1D death values: $W = B(G) \cup D(G)$.

2 Method

Barcodes in Graph Filtration. Consider a network represented as a weighted graph $G=(V,w)$ comprising a node set V and edge weights $w=(w_{ij})$ with positive and unique weights. The number of nodes and edges are denoted by |V| and |E|. Network G is a complete graph with $| E | = |V| (|V| -1)/2$. The binary graph $G_\epsilon =(V,w_\epsilon )$ of G is defined as a graph consisting of the node set V and binary edge weight $w_{\epsilon ,ij} =1$ if $w_{ij} > \epsilon$ or 0 otherwise. The binary network $G_{\epsilon }$ is the 1-skeleton, a simplicial complex consisting of nodes and edges only [22]. In 1-skeleton, 0-dimensional (0D) holes are connected components and 1-dimensional (1D) holes are cycles [7]. The number of connected components and cycles in the binary network $G_{\epsilon }$ are referred to as the 0-th Betti number $\beta _0(G_{\epsilon })$ and the 1-st Betti number $\beta _1(G_{\epsilon })$. A graph filtration of G is defined as a collection of nested binary networks [7, 17]: $G_{\epsilon _0} \supset G_{\epsilon _1} \supset \cdots \supset G_{\epsilon _k} ,$ where $\epsilon _0< \epsilon _1< \cdots < \epsilon _k$ are filtration values. By increasing the filtration value $\epsilon$, we are thresholding at higher connectivity resulting in more edges being removed, and thus the 0-th and 1-st Betti numbers change.

Persistent homology keeps track of appearances (birth) and disappearances (death) of connected components and cycles over filtration values $\epsilon$, and associates their persistence (lifetimes measured as the duration of birth to death) to them. Long lifetimes indicate global topological features while short lifetimes indicate small-scale topological features [11, 20, 29]. The persistence is represented by 0D and 1D barcodes comprising a set of intervals $[b_i,d_i]$, each of which tabulates a lifetime of a connected component or a cycle that appears at the filtration value $b_i$ and vanishes at $d_i$ (Fig. 2). Since connected components are born one at a time over increasing filtration values [7], these connected components will never die once they are born. Thus, we simply ignore their death values at $\infty$ and represent 0D barcode as a set of only birth values $B(G) = \cup _i \{b_i \}$. Cycles are considered born at $-\infty$ and will die one at a time over the filtration. Ignoring the $-\infty$, we represent 1D barcode as a set of only death values $D(G)=\cup _i \{ d_i \}$.

Theorem 1

The set of 0D birth values B(G) and 1D death values D(G) partition the weight set $W=\{w_{ij}\}$ such that $W = B(G) \cup D(G)$ with $B(G) \cap D(G) = \emptyset$. The cardinality of B(G) and D(G) are $|V|-1$ and $1 + \frac{|V| (|V| - 3)}{2}$ respectively.

The proof is given in the supplementary material. Finding 0D birth values B(G) is equivalent to finding edge weights of the maximum spanning tree (MST) of G using Prim’s or Kruskal’s algorithm [17]. Once B is computed, D is simply given as the remaining edge weights. Thus, the barcodes are computed efficiently in $O(|E| \log |V|)$.

Topological Loss. Since networks are topologically completely characterized by 0D and 1D barcodes, the topological dissimilarity between two networks can be measured through barcode differences. We adapt the Wasserstein distance to quantify the differences between the barcodes [9, 15, 23]. The Wasserstein distance measures the differences between underlying probability distributions on barcodes through the Dirac delta function [10]. Let $\varTheta =(V,w^{\varTheta })$ and $P=(V, w^P)$ be two given networks. The topological loss $\mathcal {L}_{top}(\varTheta ,P)$ is defined as the optimal matching cost

$$\begin{aligned} \mathcal {L}_{top}(\varTheta ,P) = \min _{\tau _0} \sum _{b \in B(\varTheta )} \big [ b - \tau _0(b)\big ]^2 + \min _{\tau _1} \sum _{d \in D(\varTheta )} \big [ d - \tau _1(d)\big ]^2 , \end{aligned}$$

(1)

where $\tau _0$ is a bijection from $B(\varTheta )$ to B(P) and $\tau _1$ is a bijection from $D(\varTheta )$ to D(P). By Theorem 1, the bijections $\tau _0$ and $\tau _1$ always exist. The first term measures how close two networks are in terms of 0D holes (connected components) and is referred to as 0D topological loss $\mathcal {L}_{0D}$. The second term measures how close two networks are in terms of 1D holes (cycles) and is called 1D topological loss $\mathcal {L}_{1D}$. Connected components represent an integration of a brain network while cycles represent how strong the integration is [6]. The optimization can be done exactly as follows:

Theorem 2

$$\begin{aligned} \mathcal {L}_{0D} = \min _{\tau _0} \sum _{b \in B(\varTheta )} \big [ b - \tau _0(b)\big ]^2 = \sum _{b \in B(\varTheta )} \big [ b - \tau _0^*(b)\big ]^2, \end{aligned}$$

(2)

where $\tau _0^*$ maps the i-th smallest birth value in $B(\varTheta )$ to the i-th smallest birth value in B(P) for all i.

$$\begin{aligned} \mathcal {L}_{1D} = \min _{\tau _1} \sum _{d \in D(\varTheta )} \big [ d - \tau _1(d)\big ]^2 = \sum _{d \in D(\varTheta )} \big [ d - \tau _1^*(d) \big ]^2, \end{aligned}$$

(3)

where $\tau _1^*$ maps the i-th smallest death value in $D(\varTheta )$ to the i-th smallest death value in D(P) for all i.

The proof is given in the supplementary material. We can compute the optimal matchings $\tau _0^*$ and $\tau _1^*$ between $\varTheta$ and P in $O \big ( |B(\varTheta )| \log |B(\varTheta )| \big )$ and $O \big ( |D(\varTheta )| \log |D(\varTheta )| \big )$ by sorting edge weights and matching them.

Topological Learning. Let $G_1=(V, w^1), \cdots ,G_n=(V, w^n)$ be observed networks used for training a model. Let $P=(V, w^P)$ be a network expressing a prior topological knowledge. In brain network analysis, $G_k$ can be a functional brain network of k-th subject obtained from resting-state fMRI, and P can be a template structural brain network obtained from dMRI. The functional networks can then overlay the template network (Fig. 1).

We are interested in learning the model $\varTheta =(V,w^{\varTheta })$ using both the functional and structural brain networks. At the subject level, we train $\varTheta$ using individual network $G_k$ by optimizing

$$\begin{aligned} \widehat{\varTheta }_k = \mathop {\mathrm {arg\,min}}\limits _\varTheta \mathcal {L}_F(\varTheta ,G_k) + \lambda \mathcal {L}_{top}(\varTheta ,P), \end{aligned}$$

(4)

where the squared Frobenius loss $\mathcal {L}_F(\varTheta ,G_k) = ||w^\varTheta -w^k||^2_F$ measures the goodness of fit between the model and the individual network. The parameter $\lambda$ controls the amount of topological information of network P that is introduced to $G_k$. The larger the value of $\lambda$, the more we are learning toward the topology of P. If $\lambda =0$, we no longer learn the topology of P but simply fit the model $\varTheta$ to the individual network $G_k$.

In numerical implementation, $\varTheta = (V, w^{\varTheta })$ can be estimated iteratively through gradient descent efficiently by Theorems 1 and 2. The topological gradient with respect to edge weights $w^{\varTheta } = (w_{ij}^{\varTheta })$ is given as

$$\begin{aligned} \frac{\partial \mathcal {L}_{top}(\varTheta ,P)}{\partial w_{ij}^{\varTheta }} = {\left\{ \begin{array}{ll} 2 \big ( w_{ij}^{\varTheta } - \tau _0^*( w_{ij}^{\varTheta } ) \big ) &{} \text {if } w_{ij}^{\varTheta } \in B(\varTheta ); \\ 2 \big ( w_{ij}^{\varTheta } - \tau _1^*(w_{ij}^{\varTheta } ) \big ) &{} \text {if } w_{ij}^{\varTheta } \in D(\varTheta ). \end{array}\right. } \end{aligned}$$

(5)

By updating the edge weight $w_{ij}^{\varTheta }$, we adjust either a 0D birth value or a 1D death value, which changes topology of the model $\varTheta$. At each current iteration, we take a step in the direction of negative gradient with respect to an updated $\varTheta$ from the previous iteration. As $w_{ij}^{\varTheta }$ is moved through its optimal matching, the topology of $\varTheta$ gets close to that of P while the Frobenius norm keeps $\varTheta$ close to the observed network $G_k$. The time complexity of topological gradient is dominated by the computation of the MST with $O(|E| \log |V|)$.

Fig. 3.

(a) Two modular networks with $d=24$ nodes and $c=3$ modules were generated using $p=0.6$ and 0.8. (b) The run time of graph matching cost between two modular networks of node size d plotted in the logarithmic scale. The run time of topological loss grows in a minuscule rate with the node size as opposed to the exponential run times of the graph matching algorithms.

3 Statistical Validation

We evaluated discriminative performance of the topological loss against four well-known graph matching algorithms: graduated assignment (GA) [13], spectral matching (SM) [18], integer projected fixed point method (IPFP) [19] and re-weighted random walk matching (RRWM) [5] using simulated networks.

We simulated random modular network $\mathcal {X}$ with d number of nodes and c number of modules where the nodes are evenly distributed among modules. We used $d=12,18,24$ and $c=2,3,6$. Each edge connecting two nodes within the same module was then assigned a random weight following a normal distribution $\mathcal {N}(\mu ,\sigma ^2)$ with probability p or Gaussian noise $\mathcal {N}(0,\sigma ^2)$ with probability $1-p$. Edge weights connecting nodes between different modules had probability $1-p$ of being $\mathcal {N}(\mu ,\sigma ^2)$ and probability p of being $\mathcal {N}(0,\sigma ^2)$. Any negative edge weights were set to zero. With larger value of within-module probability p, we have more pronounced modular structure (Fig. 3-a). The network $\mathcal {X}$ exhibits topological structures of connectedness. $\mu =1$, $\sigma =0.25$ and $p=0.6$ were universally used as network variability.

We simulated two groups of random modular networks $\mathcal {X}_1,\cdots ,\mathcal {X}_m$ and $\mathcal {Y}_1,\cdots ,\mathcal {Y}_n$. If there is group difference in network topology, an average topological loss within group $\overline{\mathcal {L}}_{W} =\frac{\sum _{i< j} \mathcal {L}(\mathcal {X}_i,\mathcal {X}_j) + \sum _{i < j} \mathcal {L}(\mathcal {Y}_i,\mathcal {Y}_j)}{{m \atopwithdelims ()2} + {n \atopwithdelims ()2}}$ is expected to be smaller than an average topological loss between groups $\overline{\mathcal {L}}_{B}=\frac{\sum _{i=1}^m \sum _{j=1}^n \mathcal {L}(\mathcal {X}_i,\mathcal {Y}_j)}{mn}.$ We measured the group disparity as the ratio statistic $\phi _\mathcal {L} = \overline{\mathcal {L}}_{B}\Big / \overline{\mathcal {L}}_{W}.$ If $\phi _\mathcal {L}$ is large, the groups differ significantly in network topology. If $\phi _\mathcal {L}$ is small, it is likely that there is no group difference. Similarly, we also defined the ratio statistic for the baseline algorithms. Since the distributions of the ratio statistics were unknown, the permutation test was used. In each simulation, we generated two groups with 10 modular networks each. We then computed 200000 permutations by shuffling group labels and obtained the p-values. The simulations were independently performed 50 times and the average p-value was reported.

Table 1. Performance results are summarized as average p-values for various parameter settings of d (number of nodes) and c (number of modules).

The baseline graph matching algorithms are of polynomial time and not scalable compared to our method. For networks with $d=100$ nodes, the run times of all the baselines are more than 100 times longer than that of topological loss (Fig. 3-b). When there is network difference (first three rows in Table 1), small p-value indicates that a method performs well at discriminating networks. In all the parameter settings, topological loss outperformed the other graph matching algorithms. Topological loss also consistently outperformed the baseline algorithms for other values of c, d and p. In the case of no network difference (last row in Table 1), small p-value indicates a method falsely detects the network difference when there is none. Since p-values of all the methods were not statistically significant, they all performed well. We also get similar results for other values of c, d and p. The graph matching algorithms are unable to detect topological differences while topological loss is able to easily detect such differences in subtle topological patterns with the minimal amount of run time. The MATLAB code for the simulation study is available at https://topolearn.github.io/topo-loss. The SM algorithm used in this simulation study and methods proposed in [1, 26] rely on the same spectral graph theory and are expected to show analogous performance results.

Fig. 4.

Most heritable connections with 100% heritability using (a) Pearson correlation matrices and (b) topologically learned networks.

4 Application to a Twin Imaging Study

Dataset and Preprocessing. dMRI and resting-state fMRI data were obtained from the Human Connectome Project [28]. fMRI went through further preprocessing including motion correction, scrubbing, bandpass filtering and outlier removal among others. AAL was used to parcellate the brain into 116 regions [27]. fMRI were spatially averaged across voxels within each brain region resulting in 116 average fMRI time series per subject. There are 124 monozygotic (MZ) twin pairs and 70 same-sex dizygotic (DZ) twin pairs. For dMRI, about one million fiber tracts per subject were generated to compute biologically accurate brain connectivity [8]. AAL was used to parcellate the brain into 116 regions. The subject-level connectivity matrices were constructed by counting the number of tracts between the regions. The template structural network P was obtained by computing one sample t-statistic map over all the subjects and rescaling the t-statistic between 0 to 2 through the hyperbolic tangent function then adding 1 (Fig. 1). The t-statistic map from [8] is made publicly available at http://stat.wisc.edu/~mchung/softwares/dti.

Genetic Heritability. For the k-th subject, functional connectivity $\rho ^k_{ij}$ between regions i and j was computed using the Pearson correlation between time series. We converted the correlation into a metric through $w^k=(w_{ij}^k)$, where $w_{ij}^k = \sqrt{(1-\rho ^k_{ij})\big /2}$ and obtained a subject-level functional brain network $G_k = (V, w^k)$ [7]. The topological learning was applied to estimate the subject-level model $\varTheta _k$ by minimizing the objective function (4) using the individual network $G_k$ and the template structural network P. The model $\varTheta _k$ was initialized to $G_k$. To determine an optimal subject-level $\lambda$, we searched over different $\lambda$’s to find a value that minimized the total loss $\mathcal {L}_F + \mathcal {L}_{top}$ for each subject. The average of the optimal $\lambda$’s across all the subjects was $\lambda = 1.0000\pm 0.0002$, a highly stable result. Thus, we globally used $\lambda =1$ for all the subjects. We then investigated if the learned networks $\widehat{\varTheta }_k$ are genetically heritable. We used the ACE model where the heritability index (HI) is estimated using Falconer’s formula [6].

Results and Discussion. We computed the HI using the initial Pearson correlation matrices as a baseline versus the topologically learned networks. Figure 4, which displays resulting HI thresholded at 100% heritability, shows far more connections for the learned networks as opposed to the Pearson correlation matrices. The learned networks are expected to inherit sparse topology without many cycles from the template network P (Fig. 1). This suggests that short-lived cycles were removed from the initial functional networks, improving the statistical sensitivity. For the learned networks, the connection with the highest HI is between left superior parietal lobule and left amygdala among many other connections with 100% heritability, suggesting that genes influence the development of these connections. Our findings can be used as a baseline for studying more complex relations between brain networks and other phenotypes.