Keywords

1 Introduction

Cutting stock problems (CSP) are one the most studied optimization problems in literature due to their high complexity and wide usage in industrial applications [2, 19].

Wascher [26] describe a CSP as: given a set of large objects (input, supply) and a set of small items (output, demand) (all of them defined with n number of geometric dimensions), the objective is to build subsets with one or more items and assign them to one of the large objects, holding the geometric constraints. In practice, this is commonly translated into the optimization of material usage (material waste reduction) in processes like cutting, trimming, or die-cutting.

Some classifications of CSPs are considered as highly complex problems (NP-Hard). It is possible to find an optimal solution for a small-sized CSP instance; however, these instances are unusual in real industrial planning decisions [7]. Heuristic approaches have been widely studied and allowed to find feasible solutions for large-scale instances in a wide variety of production-related problems [19, 20]. Recently, with the advances in data processing, computing, and relaxation methods, some real problems can now be solved using exact approaches [6].

The aim of this paper is to show the application of a mixed-integer linear programming (MILP) model for solving real instances of a one-dimensional cutting stock problem (1D-CSP). The objective is to minimize the waste in a steel bar production process considering the geometric constraints and the inventory availability.

A case study is presented and includes instances from one of the most important metallurgical companies in Colombia. In this country, the steel industry shares approximately \(10\%\) of the national economy. Also, it generates approximately \(12.12\%\) of the country’s total sales and nearly \(13.44\%\) of its jobs.

This paper is organized as follows: Sect. 2 includes a brief description of the 1D-CSP. A literature review is presented in Sect. 3, the case study is presented in Sect. 4, and the proposed solution approach is outlined in Sect. 5, including the description of the proposed MILP model. Computational results for the generation and solution of instances, and a brief comparison of solution methods are shown in Sect. 6. Finally, the main conclusions are summarized in Sect. 7.

2 Problem Description

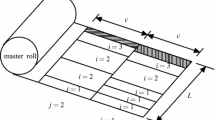
The 1D-CSP is one of the most popular combinatorial optimization problems, and it is a generalization of the well-known Bin Packing Problem (BPP). According to Kantorovich [14], the 1D-CSP is defined as follows: given two-element sets, a large object set (\(I=\{ 1,...,i,...,u \}\)) and a small item set (\(J=\{ 1,...,j,...,m \}\)), all of them in one geometric dimension. The first set is the input of the problem (e.g., raw material), and the second set is the output (e.g., finished product). Each object has an integer capacity c, i.e., geometric limitations such as width or height. The items have an integer demand \(d_j\) and a geometric size (width or height) \(w_j\). The BPP is a specific case of the 1D-CSP when the demand of each item j is equal to one (\(d_j=1\)). Both problems are NP-hard in the strong sense, and the demonstration was done through the transformation from 3-Partition problem.

3 Literature Review

There are several variants of the cutting and packing problem. However, a common objective is obtaining a set of items that fit into given stock objects [3, 4, 12, 15]. In this section, we focus on the main contributions for solving the 1D-CSP, which is closely related to the problem presented in the case study in Sect. 4.

In 1960 [14], an integer linear programming model for the 1D-CSP was proposed. However, only small-size instances could be solved by this model due to the considerable amount of cut combinations.

Later, Gilmore [11] proposed an integer linear model for the CSP, based on the “pattern” concept. A pattern is one of all combinations of items that can fit into an object, holding the geometric constraints. Compared with the model proposed by [14], the patterns-based model had a better integrality gap without symmetric solutions. However, the major drawback of this model was that the number of patterns grew exponentially.

Dyckhoff [8, 9] was one of the first authors that proposed a typology of cutting and packing problems. This topology considers four characteristics: Dimensionality, Kind of assignment, Assortment of large objects, and Assortment of small items. However, some problems can be classified into several categories, and two different problems could fit into the same category.

Valerio De Carvalho [22] proposed an arc-flow based formulation for the CSP. The objective function was to minimize the flow of an acyclic directed graph \(G=(V,A)\), where a complete path represents each pattern. The main disadvantage of this exact algorithm was the growing number of constraints.

In 2007 Wascher [26] proposed a new classification based on [9], adding a new criterion: the shape of the small items. The difference between these typologies is that the first one presents a complete problem hierarchy. Pure, basic, intermediate, refined, standard, non-standard, and special problems are considered.

Several studies have tried to improve the performance of Integer Programming models using Column Generation (CG) [16], Brand and Bound (B&B), Branch and Price [23], and Cutting Plane (CP) approaches [24].

Rothe et al. [21] proposed a two-stage three-dimensional guillotine cutting stock problem with usable leftover, allowing rotating items.

In 2018, a comparative study of exact methods for the bi-objective 1D-CSP was studied by [10]. The proposed bi-objective model aims to minimize the frequency and the number of different cutting patterns, being these conflicting objectives. However, with the contributions in exact algorithms, 1D-CSP large-scale instances cannot be optimally resolved in a reasonable computational time.

Therefore, CSPs have been also addressed using approximate methods. These procedures do not guarantee an optimal solution but can achieve a near-optimal solution in short computational time. The approximate methods applied to the 1D-CSP are grouped into two sets: heuristic methods [5, 19, 25] and meta-heuristics approaches [1, 13, 27].

Some specific cases in the steel industry include efforts from Moussavi et al. [18] who presented an optimization approach for minimizing the cutting waste from reinforcing bars in the construction of concrete structures. The model considers lap splicing patterns flexibility, and results showed improvements up to 55.7% in steel waste reduction.

Maher et al. [17] showed the implementation results of a control system for the steel reinforcements industry. The system merged a one-dimensional cutting stock algorithm and a leftover control algorithm.

Despite the high complexity of the 1D-CSPs, some real instances could deal with a significant number of patterns through constraints associated with the cutting process. Some of those instances can be optimally solved using integer programming. In this paper, a cutting pattern generation procedure is proposed and a solving method was validated for large instances in reduced computational times.

4 Case Study

The case study takes place in a metallurgic company in the state of Valle del Cauca, Colombia. The company has a steel production capacity of 1800 tons per month. The cutting process begins when an order arrives, and it contains the demand of a given number of bars of different sizes (small items).

The company implemented an empirical cutting procedure (Company Method) to minimize the number of different item sizes per lot. For example: There are two orders: the first order contains 20 pieces of 6 m, and the other order contains 35 pieces of 12 m. Under this method, the company will produce the total number of 6-m pieces consecutively and then produce the total number of 12-m pieces. This cutting method generates high amounts of waste.

There are some particular considerations of the cutting process that must be taken into account:

  1. 1.

    The demand for small items is known and grouped by customer.

  2. 2.

    There is limited space for storage in the production area.

  3. 3.

    Each cut could be performed in a steel bar (large object) of 6 m, 9 m, 10 m, 11 m, 12 m or 14 m.

  4. 4.

    The length of the cuts could be as long as the assigned steel bar.

  5. 5.

    A cutting pattern can include a maximum of two types of small items.

  6. 6.

    The exceeding material in the cutting process is classified as waste or leftover depending on the piece’s length. Leftovers are pieces that can be used to make other cuts in the next production cycle, and the waste is material that has to be discarded.

5 Solution Approach

The process for obtaining a solution for the 1D-CSP is shown in Fig. 1. A set of feasible cutting patterns was generated using the information of orders of small items (bars of different sizes) and inventory records of large objects (quantities and specifications of standard steel bars). The feasible patterns were generated considering all geometric constraints and were set as parameters in the proposed MILP model. Finally, a 1D-CSP solution was obtained for every order.

Fig. 1.
figure 1

Solution approach for the 1D-CSP.

Full size image

5.1 Cutting Patterns Generation Algorithm

Formally, a pattern p can be defined by an integer array \((a_{1p}, a_{2p},..., a_{mp})\), where each \(a_{jp}\) is the number of copies of item j that are contained in p. Patterns are feasible when they fulfill the geometric constraints.

figure a
Fig. 2.
figure 2

Pattern representations

Full size image

Figure 2 shows some cutting pattern representations. Unfeasible Patterns are not allowed (in this case, the pattern included more than two different types of small items). Special Patterns have leftover, Normal Patterns have waste material, and Efficient Patterns have neither leftover nor waste.

Algorithm 1 was used to generate feasible cutting patterns, according to geometric constraints, and taking into account the particular considerations of the cutting process (Sect. 4). Cutting patterns are generated considering the use of leftovers and with a maximum of two types of small items in a single cutting pattern. This constraint allows reducing the complexity of the problem, reducing the total number of feasible solutions.

5.2 Proposed MILP Model

The following Mixed Integer Linear Programming model has been proposed to improve production planning efficiency and minimize the total steel waste.

Sets

  • \(S= \{1, ..., s, ..., q\}\) set of special patterns.

  • \(N= \{1, ..., n, ..., m\}\) set of normal patterns.

  • \(I=\{1, ..., i, ..., b\}\) set of small items.

  • \(P=\{6,9,10,11,12,14\}\) set of large objects, i.e. available lengths [meters].

  • \(K_l \subset S \mid l \in P\) subset of special patterns with object of length l.

  • \(J_l \subset N \mid l \in P\) subset of normal patterns with object of length l.

Parameters

  • \(N_n\): waste generated by each normal pattern n.

  • \(E_s\): trim loss generated by each special pattern s.

  • \(D_i\): quantity to produce from each required bar i

  • \(CN_{in}\): quantity of bars i obtained by using the normal pattern n.

  • \(CE_{is}\): quantity of bars i obtained by using the special pattern s.

  • \(C_l \mid l \in P\) : quantity of bars of length l available in inventory.

Variables

  • \(X_n\): number of times the normal pattern n is used.

  • \(Y_s\): number of times the special pattern s is used.

Objective Function and Constraints

$$\begin{aligned} Minimize: z = \sum _{n=1}^{m} N_n * X_n + \sum _{s=1}^{q} E_s * Y_s \end{aligned}$$
(1)

s.t.

$$\begin{aligned} \sum _{n=1}^{m} CN_{in} * X_n + \sum _{s=1}^{q} CE_{is} * Y_s = D_i, \quad \forall i \in I \end{aligned}$$
(2)
$$\begin{aligned} \sum _{n \in J_l} X_n + \sum _{s \in K_l} Y_s \le C_l, \quad \forall l \in P \end{aligned}$$
(3)
$$\begin{aligned} n=\{1,\ldots ,m\}, \quad s=\{1,\ldots ,q\}, \quad X_n,Y_s\in \mathbb {Z}_+ \end{aligned}$$
(4)

The objective function (1) aims to minimize the total waste and trim loss generated by the cutting process. Constraint (2) ensures the demand fulfillment. Constraint (3) ensures production must be done with the available objects in inventory for each type of standard length. Finally, the expressions in (4) define the sets and the domain of decision variables. Two versions of the MILP model were considered: a complete model and a model without the inventory constraint (3).

6 Results

This section is divided into two parts: the first one shows the results of the proposed model in the applied case, the second part extends the experimentation to larger simulated instances.

6.1 Steel Waste Reduction in the Applied Case

An optimal solution was always found for both models: complete and without inventory constraints. The models were programmed using c++ and solved with CPLEX 12.2 through AMPL 3.5. Hardware specifications included a computer with an Intel Core i5 processor with 1.8 GHz, 8 Gb RAM. The average number of integer variables in the complete model was 8000, and the average number of constraints was 50.

According to the solution of the MILP model, waste \(N_n\) is expressed in meters. Table 1 shows the weight conversion factor for steel bars according to their diameter.

Table 1. Weights of steel bars according diameter
Full size table

A set of six random production orders was selected and the steel waste was calculated considering the cutting patterns obtained from the company method (Sect. 4), the complete MILP model, and the MILP model without inventory constraints.

Figure 3 shows a summary of the obtained results. The vertical axis’s left side shows the steel waste in kilograms, and the right side shows the percentage of improvement (PI) in steel waste reduction. In Eq. (5), \(w_c\) represents the waste generated using the company method, and \(w_{MILP}\), represents the waste generated with the complete MIP model.

$$\begin{aligned} PI= \frac{w_c - w_{MILP}}{w_c}*100 \end{aligned}$$
(5)
Fig. 3.
figure 3

Computational results.

Full size image

According to every solution method, the horizontal axis shows the obtained results of steel waste for the six random production orders.

Results showed that the complete MIP model outperforms the company method in all instances. The average improvement was \(80\%\), with a minimum of \(55.3\%\), and a maximum of \(99.6\%\). There were no significant differences between the complete model and the model without inventory constraints.

6.2 Computational Complexity Experiments

A total of 100 random instances were generated to perform the computational experiments. The instances included all the possible combinations of 10 types of Large Objects (LE, by its Spanish acronym) and a set of 10 types of small items (LD, by its Spanish acronym). The instance generation considered the minimum values for LD and LE, which increased by 12 centimeters to obtain the 10 types of parts. The maximum and minimum quantity of each part was randomly generated based on the range of actual demands.

Figure 4 shows the average time (in seconds) spent to create all cutting patterns as a function of LD and LE. Due to the limitations of the cutting process, the pattern generation procedure was efficient. Although the largest instances only took about 80 s to be generated, the number of patterns began to grow exponentially, resulting in plain text files with more than 300 MB of pattern information. This increasing trend in the number of LD and LE dependent patterns is observed in Fig. 5, reaching one million patterns.

Fig. 4.
figure 4

Average time (s) to create cutting patterns.

Full size image
Fig. 5.
figure 5

Number of generated patterns as a function of LE and LD.

Full size image

Despite a large number of patterns, the proposed linear programming model can solve them quickly, as can be seen in Fig. 6. The maximum time obtained for the largest instance was 2 s. However, the memory usage of the model before solving (loading it into RAM) was significantly high. It can use more than 8 Gb of memory in the largest instances. This memory usage was the main limitation of the experimentation and the reason for not making larger increments in the generation of LDs and LEs. For example, with increments of 14 centimeters, the problem could not be loaded into memory.

Fig. 6.
figure 6

Number of patterns as a function of LE and LD.

Full size image

7 Conclusions

This paper showed the results of applying a MILP model for solving actual 1D-CSP instances in the steel industry.

The solution approach considered some of the production process’s main limitations and used them to simplify the proposed MILP model. The number of feasible cutting patterns was significantly reduced, considering a limited number of different references in a single pattern.

The results between the empirical method implemented by the company, the complete exact model, and the model without inventory constraints were compared in terms of kilograms of steel waste per order. There was no significant difference between both MILP models, and the average improvement in waste reduction was \(80\%\).

The pattern generation algorithm and the MILP model were experimentally proven to be efficient, solving instances of more than one million patterns in less than 2 s. As a limitation, the memory usage is very high, preventing the execution of larger instances. Large-scale optimization methods (such as column generation, where the explicit use of all variables is not required.) are recommended, considering the memory usage limitations.

Future work opportunities include considering the integration of the MILP models into a production planning web application. Also, some additional efforts should consider alternative strategies to reduce production costs and improve the solution of large-scale instances with a larger number of constraints.