The Fall and Rise of Resemblance Diagrams

Abstract

A recent investigation of the changes in the use of diagrams in published mathematics papers shows that diagrams were frequently used at the end of the 19th century and the beginning of the 20th. They then largely disappeared in the period 1910–1950, whereafter they reappear [1]. Although this story is unsurprising considering the dominance of formalist ideology in the first half of the 20th century, the detailed investigation of the development points out several interesting open questions. Especially, we do not know if the diagrams that disappeared with the advent of formalism are the same as those that are used today.

In this paper, we will focus on so-called “resemblance” diagrams, which are one of three general categories of diagrams covered in the investigation in [1]. We will analyze and compare resemblance diagrams used in the late 19th century with those used in the early 20th century to determine if there have been substantial changes. The comparison shows that even though the diagrams can be said to belong to the same general category and share certain general features, the resemblance diagrams used today are very different from those used before the advent of formalism. The criticism raised by the formalist movement of the diagrams used in the late 19th century can be seen as a possible explanation of this change.

1 Entering the Valley of Formalism

Looking at research papers published in mathematics journals during the last century, one gets the impression that there are substantial differences in the frequency and types of diagrams published in different time periods. In [1], the overall trends and changes in the use of diagrams in the period 1885–2015 are investigated by coding all papers published in the Bulletin of the AMS, Acta Mathematica, and Annals of Mathematics in years separated by five-year intervals beginning with 1885. The investigation revealed that diagrams were relatively frequently used until 1910. Then they disappeared for several decades before they reappeared during the 1950s and 1960s. The disappearance can, in part, be ascribed to the influence of what we will loosely call “formalist ideology”, e.g., the nexus of ideas expressed by David Hilbert [3], Mouriz Pasch [4], Bertrand Russell [5], and others, that mathematics should be formalizable and that diagrammatic reasoning should be confined to the heuristics of mathematics. In other words, we see a half-a-century-wide “valley of formalism,” where diagrams almost disappear from mathematics publications.

The investigation reported in [1], however, also shows that the diagrams that reappeared in the 1950s were not the same as those that disappeared half a century earlier. To track the overall changes in the types of published diagrams, the investigation operates with a rough distinction between three general categories of diagrams: resemblance, algebraized, and abstract diagrams. Here “resemblance diagrams” are diagrams with a direct resemblance to the objects being represented, “algebraized diagrams” represent objects in an algebraized domain, and “abstract diagrams” essentially depend on a conceptual map (see [2] for details). The resurge of diagrams in the 1950s and 1960s was mainly due to the advent of abstract diagrams, especially commutative diagrams, and closely related diagram types. As diagrams of this type were rarely used at the beginning of the 20th century, it appears that the formalist ban on diagrams was not broken by the reappearance of the “old” diagrams, but rather by the introduction of a completely new kind of diagram that conforms better to the specific formalistic demands for rigor.

The data in [1], however, also show that resemblance diagrams and algebraized diagrams eventually reappeared as well, although slightly later. As the criticism of the use of diagrams in mathematics made by the formalist movement was mainly aimed at resemblance diagrams, especially diagrams involving geometric intuition, this is particularly interesting. Does the reappearance of resemblance diagrams indicate that diagrams attacked by formalism are once again used in mathematical publication practice?

Unfortunately, the three categories used to classify diagrams in [1] are very broad, and each category includes several sub-categories of diagrams. Thus, although resemblance diagrams reappeared in the late 20th century, we do not know if the resemblance diagrams that are used today are of the exact same type as those used before the advent of formalism, or if there has been an internal development within the category. In this paper, we will investigate this question by analyzing and comparing the resemblance diagrams that were published at the end of the 19th century with those published at the beginning of the 21st century. The aims of this investigation are 1) to give a more detailed picture of the influence formalist ideology has had on the use of diagrams and 2) to strengthen our understanding of the role certain types of diagrams play in modern mathematical practice.

2 Methods

The sampling and coding strategy for the full investigation is described in detail in [1, 2]. In the full corpus, 1,143 diagrams were coded as resemblance diagrams. For this paper, all diagrams coded as resemblance diagrams in the years 1885–1895 and 2005–2015 were revisited with a qualitative and grounded approach aimed at identifying relevant sub-classes of diagrams within the general category. Each subclass was given a short description, and a prototypical example of the class was picked out and will be presented below.

The number of resemblance diagrams and the distribution over the six years in question can be seen in Table 1. As the number of diagrams is relatively small, we did not attempt a structured quantitative analysis (e.g., counting the exact number of diagrams in each subclass) but restricted ourselves to a purely qualitative analysis describing the types of diagrams present in the two periods supplemented with rough estimates describing the relative frequency of the most common types.

Table 1. Resemblance diagrams in the years 1885–1895 and 2005–2015.

3 Results

3.1 Resemblance Diagrams 1885–1895

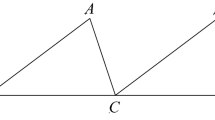
In the analysis of the resemblance diagrams published in the early period, that is, 1885, 1890, and 1895, three major sub-categories (what we will call “types”) emerged. We will call the first of these Euclidian construction diagrams. Diagrams of this type are used to anchor a sequence of geometric constructions involving basic geometric objects, such as circles, triangles, and straight lines. A prototypical example is shown in Fig. 1.

The second subcategory is object illustrating diagrams. This type of diagram is closely related to Euclidian construction diagrams, but instead of anchoring a geometric construction, these diagrams simply represent a constellation of idealized geometric shapes, often modelling real life objects. A prototypical example, where different ways of stretching a string between two objects is modeled, is shown in Fig. 2.

Fig. 1.

Reproduced with kind permission from [6, p. 176].

Euclidian diagram.

Fig. 2.

Reproduced with kind permission from [7, p.189].

Diagram illustrating an object (a string stretched between the two figures $A_1$ and $A_2$).

The final subcategory identified in the early period is diagrams illustrating an operation. Here, geometric shapes are used to illustrate the effects of an operation. Thus, in a sense, such diagrams do not illustrate the geometric shapes per se but rather something more abstract, such as an operation. A prototypical example is shown in Fig. 3.

Fig. 3.

Reproduced with kind permission from [8, p.4].

Diagram illustrating the effect of an operation on a geometric shape.

In the period in question, Euclidian construction diagrams are the most common of the three types, closely followed by diagrams illustrating objects. Only one paper contains diagrams illustrating operations. From this analysis, it thus follows that in our corpus, the resemblance diagrams used in the period 1885–1895 had a close connection to specific geometric objects either by anchoring compass and straightedge constructions or by modeling (metric properties of) constellations of geometric shapes.

3.2 Resemblance Diagrams 2005–2015

Diagrams illustrating objects and those illustrating operations are also present in the late period (viz. 2005, 2010 and 2015). Yet, most of the diagrams illustrating objects are of a slightly different nature than the similar diagrams in the early period. In the early period, the resemblance between the object and the diagram illustrating the object is established through direct metric likeness, whereas in the late period, the resemblance is most often established through topological likeness. We consider this to be a new type of diagram that we will call a topological illustration diagram. The objects illustrated in this kind of diagram can be certain kinds of knots, graphs, and abstract objects, such as manifolds. As an example, the diagram represented in Fig. 4 is used to illustrate a proof of why the neck of a dumbbell pinches before the bells become extinct. Notice, however, that although the objects are generalized manifolds, the diagram draws heavily on intuitions based on sensory-motor experience.

Among the 578 resemblance diagrams in the late part of the corpus, we did not encounter any Euclidian construction diagrams. However, another kind of construction diagrams are very common. These diagrams can be called topological construction diagrams, and they can be characterized as diagrams representing constructions with or on objects of topological illustration diagrams. As a prototypical example, Fig. 5 illustrates how two abstract surfaces can be glued together. In this period, there is a thin line between representing objects and constructions, as the representation diagrams often suggest movement or manipulation of the objects represented, although this is not explicitly stated, as the implied pinching of the surfaces in Fig. 4 illustrates.

Fig. 4.

Reproduced with permission from [9, p. 303].

Diagram illustrating an object through topological likeness. In this case the diagram illustrates a vital step in a proof by Angenent.

Fig. 5.

Reproduced with permission from [10, p. 62].

A topological construction diagram).

Thus, in short, in both periods, we see resemblance diagrams illustrating objects and diagrams representing constructions. However, there is a crucial difference between the two periods in the sense that in the early period the resemblance is established through metric likeness, whereas in the late period it is (mostly) established through topological likeness. We will explain why this distinction is crucial in the discussion below.

Apart from the move from metric to topological likeness, we also saw some qualitatively new types of diagrams in the late period. Especially, a diagram type we will call syntactic manipulation diagrams is widely used in the late period. In these diagrams, the objects represented are also transformed, but not as freely as in the topological construction diagrams, but rather in accordance with strict syntactic rules. This in effect turns this type of diagram into a hybrid between diagrams and symbols (as pointed out in [11]). A prototypical example is Reidemeister moves representing manipulations of idealized knots (Fig. 6). This general type of diagram, however, is widespread in the late part of the corpus, and the specific diagrams belonging to this type are often innovative and appear to play a central role in the arguments of the papers in which they appear. As an example, in [13], a particular type of “puzzle piece” is introduced along with rules of manipulation, and diagrams constructed with these puzzle pieces are then used to perform complex calculations within the particular area of mathematics at hand (see Fig. 7 and Fig. 8). We have coded all representations involving these puzzle pieces in [13] to be diagrammatic, although there may be little difference between the arrangement seen in Fig. 8 and an arrangement of algebraic symbols in the sense that calculations can (seemingly) be performed as purely syntactic manipulations with both representational types. The hybrid nature of syntactic manipulation diagrams thus makes it difficult to maintain a clear distinction between algebraic and diagrammatic representations.

Fig. 6.

Reproduced with kind permission from [12, p. 500].

Diagram illustrating a particular Reidemeister move on an idealized knot.

Fig. 7.

Reproduced with kind permission from [13, p. 179].

Partial explanation of the syntax of the “puzzle piece” diagrams.

Fig. 8.

Reproduced with kind permission from [13, p. 180].

Puzzle pieces needed for a particular computation.

There is extensive variety in the types of diagrams used in the late part of the corpus—both in general and within the category of resemblance diagrams, which is our focus point in this paper. The sub-categories we have presented here do not cover all the resemblance diagrams in the late part of the corpus, only what we believe to be the most common types of diagrams. This explosion in the variety of diagram types and designs is by itself an interesting result worth noticing; the fact that contemporary mathematicians are willing to spend the effort needed to design and typeset new—often complex—diagram types suggests that diagrams play a relatively central role in their practice (as also pointed out in [1]).

4 Discussion

In summary, we see considerable differences between the resemblance diagrams present in the two parts of the corpus under investigation here. The type of diagrams most commonly used in the years 1885–1895, Euclidian construction diagrams, was not at all present in the late period, and the two other diagram types used in the early period are rarely used in the same form in the years 2005–2015. As a clear trend, the use of metric likeness in the early period is generally (although not completely) replaced with topological likeness in the late period. We thus see diagrams illustrating objects and anchoring constructions in both parts of the corpus, but in contrast to the early period, these diagrams most often take departure in topological likeness in the late period rather than metric likeness. Furthermore, syntactic manipulation diagrams are extensively used in the late period, whereas they are not present in the early period (in the part of our corpus under investigation here).

Following this analysis, it is especially worth noting that the resemblance diagrams used in the late period are better suited to answer at least part of the criticism raised against the use of diagrams in mathematical reasoning. A typical point of criticism centers on the idea that diagrams are over-specific and thus do not allow general conclusions (although this can be contested, see e.g. [14]). Another typical criticism points out that reasoning with the exact features of a diagram may lead to false conclusions (e.g., in the famous example of the “proof” that all triangles are isosceles used by Hilbert [3, p.541]). This kind of criticism is much easier to raise against diagrams that depend on metric likeness, such as Euclidian construction diagrams, than against those depending on topological likeness, as the latter type is more abstract than the former (since metric features are abstracted away in topological diagrams). The move from metric to topological likeness can thus, in part, be seen as a response to the criticism raised by the formalist movement. Similarly, syntactic manipulation diagrams are well aligned with formalist ideology’s understanding of rigor, as the diagrams can (in part) be operated syntactically without the use of geometric intuition in a manner similar to algebraic symbols.

Thus, the narrative that diagrams disappeared from published mathematical material at the beginning of the 20th century and reappeared half a century later is much too simple. The development in the attitude toward and use of diagrams in the 20th century not only led to the introduction of a qualitatively new category—abstract diagrams—but, as the in-depth analysis of resemblance diagrams above has shown, it also led to substantial revisions of other categories, leading to a diagrammatic practice that is better aligned with formalist ideology. The return of diagrams thus does not indicate that formalism has been abandoned. Rather, some of its basic ideas seem to have been embedded in current diagrammatic practice.

Finally, it should be noted that the development in diagrammatic practice cannot be understood solely as the product of ideological development. Other factors such as technological development and changes in research interests, should also be taken into consideration. These are not disconnected; it would be difficult to pursue a research interest in an area of mathematics that depends heavily on diagrams if you do not have the technical means to produce them and if current ideology forbids their publication. We have chosen to focus on ideology as an explanatory factor in this short paper, but the story could clearly be nuanced taking other factors into consideration as well.