Keywords

1 Introduction

In the case of rubber-like materials, the volumetric compressibility modulus is a few orders of magnitude larger than the shear modulus \({\text{K}}_{0} > > {\upmu }_{0}\) [1,2,3]. Therefore, when interpreting typical experimental results of uniaxial and biaxial stretching and simple shear, universal relationships resulting from the adoption of incompressible hyperelastic constitutive relationships are used [3, 4]. A significant number of papers proposed constitutive equations for rubber-like materials, see for examples [3] and extensive source literature cited there.

In the case of hyperelasticity, many different constitutive relations are used to describe the nonlinear, elastic properties of a given material, with their similar agreement with experimental data. These tests usually concern the analysis of homogeneous deformations of the tested material samples. Based on the comparison of the results of these tests with the theoretical formulas resulting from the constitutive relation, material parameters are determined. Therefore, the validation of hyperelasticity models also requires the interpretation of the results of experiments where non-uniform deformations occur. Then it is necessary to obtain solutions to some boundary value problem of hyperelasticity. In this paper, we focus on modelling a rubber cylindrical tube in the finite element method software ABAQUS [5]. This problem is known as an excellent example of a benchmark problem in an evaluation of numerical results [6,7,8,9].

In the work, we follow the standard tensor notation of the mechanics of continuous media and the theory of hyperelasticity [10, 11].

2 Hyperelastic Incompressible Material Models

A large number of hyperelastic incompressible rubber-like material models are considered in the literature [3, 4]. For the sake of clarity, we present relevant stored energy functions here as well.

A five-parameter polynomial model (called MV) is given by

$$ \begin{gathered} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{W}_{MV} \left( {\overline{I}_{1} ,\overline{I}_{2} } \right) = \frac{1}{2}\left[ {a_{1} \left( {\overline{I}_{1} - 3} \right) + \frac{1}{2}a_{2} \left( {\overline{I}_{1}^{2} - 9} \right) + \frac{1}{3}a_{3} \left( {\overline{I}_{1}^{3} - 27} \right)} \right.\, \\ \left. + {a_{4} \left( {\overline{I}_{2} - 3} \right) + a_{5} \left( {\overline{I}_{1} \overline{I}_{2} - 9} \right)} \right], \\ \end{gathered} $$
(1)

where \(\overline{I}_{1} ,\overline{I}_{2}\) denote the invariants of the modified right and left Cauchy-Green deformation tensors. The model states a third-order consistent polynomial expansion of the stored energy function. The Mooney model is a special case of Eq. (1) such that

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{W}_{MR} \left( {\overline{I}_{1} ,\overline{I}_{2} } \right) = \frac{1}{2}\left[ {a_{1} \left( {\overline{I}_{1} - 3} \right) + a_{4} \left( {\overline{I}_{2} - 3} \right)} \right] $$
(2)

which reduces to the neo-Hookean model if \(a_{4} = 0\). Another considered model called EXP-PL one [4], which is not of polynomial type, reads

$$ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\smile}$}}{W}_{EXP - PL} \left( {\overline{I}_{1} ,\overline{I}_{2} } \right) = \frac{\mu }{2a}\left( {e^{{a\left( {\overline{I}_{1} - 3} \right)}} - 1} \right) + b\left( {\overline{I}_{1} - 3} \right) + c\left( {\overline{I}_{2} - 3} \right). $$
(3)

The function Eq. (3) is polyconvex if the parameters are positive. For more details, we refer the reader to [4].

Table 1. Parameters for Alexander’s data [12] (neoprene)
Full size table

Figure 1 presents nominal stress vs principal stretch for Alexander’s experimental data on neoprene [12]. Parameters are shown in Table 1. It should be noted that MV and EXP-PL models accurately describe the data for large deformations which is not the case for NH or MR material models. However, the range of small deformations is not sufficiently accurate predicted especially in the case of biaxial tension mode.

Fig. 1.
figure 1

Nominal stress vs principal stretch plots for uniaxial (UT) and biaxial (BT) tension modes in the case of Alexander’s data [12] – a) Neo-Hooekan model, b) Mooney model, c) MV model, d) EXP-PL model. Parameters are presented in Table 1.

Full size image

3 Finite Element Method Modelling of the Cylindrical Tube Problem in ABAQUS

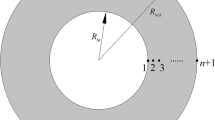
A cylindrical tube of unit length (plane-strain state) is modelled in ABAQUS using two approaches. The first one consists of a quarter of the cross-section with boundary conditions that impose symmetry. Finite elements of type CPE4H are applied (seven elements of the tube’s thickness). The internal surface is subjected to a prescribed displacement \(u_{i}\). It is worth noticing that the model does not impose an axially symmetric solution (Fig. 2).

Fig. 2.
figure 2

A cylindrical tube of unit length represents a plane stain problem.

Full size image

The other FEM model involves an axially symmetric stress formulation [5, 11]. To this end, we use CAX4H elements (seven elements in the section). Similarly to the previous case, the internal surface is subject to a prescribed displacement \(u_{i}\). Material models are implemented via UHYPER user-subroutines (Fig. 3).

Fig. 3.
figure 3

The mesh with the boundary conditions for the axially symmetric model – CAX4H elements.

Full size image

3.1 The Neo-Hookean and Mooney Models

The first test for verification numerical results concerns the neo-Hookean and the Mooney material models with the axially symmetric stress formulation. It is known that these material models produce the same in-plane stresses if the initial shear moduli match [9].

Figure 4 presents plots of the normalised Cauchy stress tensor components through the thickness of the tube. The values obtained show high accuracy as presented in Table 2, where the analytical results computed employing MATHEMATICA [13] are collected. Moreover, ABAQUS produce the outer radius \(r_{o} = 50.4381\) which fully coincides with the analytical result.

Similar results in terms of accuracy are reported in [8], where ABAQUS is employed as well to solve several benchmark problems.

Fig. 4.
figure 4

Comparison of analytical (solid lines) and ABAQUS’s results (markers), \(R_{i} = 10\), \(R_{o} = 12\), \(r_{i} = 50.\)

Full size image
Table 2. Results comparison – stress values at the four integration points are equal.
Full size table

3.2 A Comparison of FEM Models

As it is shown in the previous subsection, the axially symmetric formulation produces results of excellent accuracy. Here we focus on a comparison of the results produced by this model with the results obtained with the model involving the quarter of the cross-section. The latter does not impose the axially symmetric solution.

For this purpose, we plot the radial stress \(\sigma_{r} \left( {r_{i} } \right)\) versus the inner radius in the current configuration. First of all, we notice that only the MV model does not produce a monotonic increasing stress value, i.e., the curve shows a local maximum followed by a local minimum, see also [10, 14]. Similarly to the previous case, the model involving the axially symmetric formulation produces highly accurate results. The other one gives the same accuracy only for the neo-Hookean material model. Comparing the results of other material models, a deviation from the analytical values is notable as the inner radius increases, see Fig. 5. However, the error is significant for very large deformations.

Fig. 5.
figure 5

Comparison of ABAQUS’s results of different FEM models a) the neo-Hooekan model, b) the Mooney model, c) the MV model, d) the EXP-PL model.

Full size image

Very similar problems are considered in the monograph [3]. It is reported that besides the MV models, the Yeoh model produces a non-monotonic increase of the stress value. Besides very large stretches and displacements, a significant rotation takes place in the final configuration of the body. Thus, it is another aspect of the problem that makes it an excellent benchmark problem.

4 A Short Cylindrical Tube

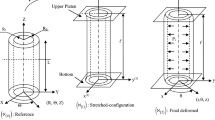
The previous sections concern a cylindrical tube problem under the plane deformation assumption, which physically may accurately approximate a sufficiently long tube. To show the behaviour of a pressurized short cylindrical tube [13], the problem illustrated in Fig. 6 is solved by employing ABAQUS (CAX4H elements). We use the MV material model.

The equilibrium path concerning the centre of the tube appears to be qualitatively similar to the one shown in Fig. 7. The different boundary conditions lead to a significantly higher value of limit point stress in comparison to the plane deformation problem. Deformations obtained characterize a typical bulging in the middle of the tube, which has been confirmed experimentally [15]. As the solution does not produce a monotonic increasing stress value, the Riks procedure is employed to obtain the path.

Fig. 6.
figure 6

A short cylindrical tube problem illustration, \(R_{i} = 10\), \(H = 2\), \(L = 20.\)

Full size image
Fig. 7.
figure 7

The radial stress \(\sigma_{r} \left( {r_{i} } \right)\) versus the inner radius in the current configuration – the centre of the tube.

Full size image

Figure 8, Fig. 9, Fig. 10 present intermediate and final configurations of the considered short cylinder inflation. It should be noted that besides very large stretches and displacements, a significant rotation takes place in the final configuration of the body. Thus, the problem should be considered in a regime of large deformations and arbitrary large rotations.

Fig. 8.
figure 8

An intermediate configuration of the short cylinder.

Full size image
Fig. 9.
figure 9

An intermediate configuration of the short cylinder.

Full size image
Fig. 10.
figure 10

The final configuration of the short cylinder.

Full size image

5 Conclusion

The cylindrical tube problem is an excellent benchmark problem in an evaluation of a numerical method. The results obtained show that the axially symmetric stress formulation in the finite element method software ABAQUS provides high accuracy for the hyperelastic material models considered. The FEM model involving CPE4H elements produces results that do not fully coincide with the analytical ones, but the formulation does not impose the axially symmetric solution. In the case of the short cylinder problem, the equilibrium path concerning the centre of the tube appears to be qualitatively similar to the one produced by the plane deformation problem’s solution. However, applied boundary conditions lead to a significantly higher value of limit point stress in comparison to the previous cases.